基于机载模型的航空动力装置的在线解耦控制

陈思成，陈淑仙，安斯奇

(中国民用航空飞行学院，四川 广汉 618307)

1 引言

航空动力装置的控制系统是一种复杂的非线性系统，工程中通常采用多变量控制方法进行控制，随着被控参数和控制回路的增多，各变量和回路间的耦合作用会越发明显，这将导致控制系统的稳定性和动态性能变差，其中在控制系统中采用解耦方法是避免上述不足的有效途径[1，2，3]。传统解耦的方法依赖于解耦补偿器与被控对象组成的广义系统传递函数矩阵为对角阵，从而实现将一个耦合影响的多变量系统化为无耦合的单变量系统[4]。但在实际的工业生产中有很多被控对象的模型都是非线性、参数未知且复杂的MIMO系统，对于航空动力装置这样的多变量控制系统更是如此，由于其工况点的变化，则传统的解耦方法是不能满足实际的控制要求的。所以之后又提出了自适应解耦控制方法，文献[5]和[6]提出的在线辨识的自适应解耦控制方法具有良好的适应性、跟踪性及解耦能力。文献[7-9]针对一类非线性的多变量系统以神经网络实现系统的在线解耦，该方法使得多变量耦合系统从静态解耦转为了动态解耦，对耦合系统具有更好的适应性。

为了简化非线性系统的解耦算法，本文提出一种基于机载(Linear Parameter Varying)LPV模型和结合传统解耦结构的在线解耦控制方法，该方法可根据实时的输入求解出动力装置对应状态下线性模型的系数矩阵，还可结合相对增益判据去判断该状态下系统的耦合程度，如果耦合程度满足判据则以前馈补偿解耦法在线生成解耦补偿对动力装置进行解耦，最终以PID控制器实现被控系统的在线解耦控制。以两输入两输出且具有强耦合特性的电力驱动变距螺旋桨动力装置为实例，验证本文所提解耦方法的有效性。

2 航空动力装置的耦合性描述

(1)

式中：α为耦合因子矩阵，其中αij=1(i=j)，v为多个输入量相互叠加后形成的新的输入向量。

从式(1)中可看出输入变量增多和耦合因子过大会都会使得变量间的耦合作用变强，导致输出量发生偏离，严重时将会使系统的控制品质变差。所以对于航空动力装置而言，在确定好控制变量后，需采取解耦方法去减弱和抵消系统内的耦合因素，使得系统的控制品质得到改善。当然最理想的情况是通过解耦后使得α=diag(1，1…，1)，系统将化为每个控制回路独立的MIMO控制系统。

3 航空动力装置的在线解耦

3.1 模型建立

对于一个航空动力装置的多变量的非线性系统的数学模型可描述为式(2)

(2)

式中：u为n维的输入向量，x为m维状态向量，y为n维的输出向量，f(x，u)和g(x，u)分别为m维状态x和n维输入u的非线性向量函数。

由于前置补偿解耦采用的是线性模型，则需要对上述的非线性模型进行线性化，即稳态点附近对其进行一阶泰勒展开[10]，再归一化处理得式(3)

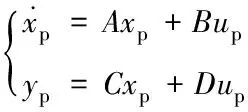
(3)

LPV模型是非线性模型的线性表达，能够反映整个包线内各工况点的情况。首先，LPV模型的建立需确立的是调度变量，且对于动力装置而言，调度变量需和动力装置的状态有关，也可将动力装置的状态作为调度变量。之后将调度变量进行等值点划分，通过辨识可求得所对应的多个稳态点附近的状态空间方程，根据对应状态下的调度变量可将系数矩阵A、B、C、D进行多项式拟合得到变参数矩阵，以此可得到航空动力装置非线性模型所对应的LPV模型，如式(5)

(4)

式中：A(ρ)、B(ρ)、C(ρ)、D(ρ)是与调度参数ρ相关的变参数矩阵。

3.2 耦合程度判断

对于多输入多输出的耦合系统，变量之间存在着耦合作用使得变量间产生了关联，在进行解耦之前需根据求解出系统传递函数以相对增益(Relative Gain Array,RGA)方法来对该系统的耦合程度进行评估[11-14]。根据稳态点附近所得到的系数矩阵A、B、C、D以系统传递函数式(5)可得解耦对象的系统传递函数矩阵。

G(s)=C(sI-A)-1B+D

(5)

式中：G(s)=(gij(s))∈Rn×n为解耦对象的传递函数矩阵，A、B、C、D为系数矩阵。

下面使用传递函数法来求解相对增益矩阵，则定义式(6)为此时系统的相对增益矩阵。

Λ=G(0)⊗(G(0)-1)T

(6)

式中：Λ=(λij)∈Rn×n，“⊗”表示矩阵的元素与元素相乘(即Hadamard乘积)。

由RGA方法可知，系统中相对增益矩阵Λ的每一个元素λij满足条件0.3，<λij<0.7时，表明关联严重，存在严重耦合，需要对该系统进行解耦[15，16]。

3.3 在线前馈补偿解耦

本文所提出的在线前馈补偿解耦是在传统的解耦方法的基础上实现的。传统的解耦结构如图1所示，如果解耦器起到作用，最理想的情况是将系统解耦后系统的传递函数矩阵GD(s)中的非主对角元素变为零，如式(7)，最后根据不变性原理[5]求解K(s)。

GD(s)=G(s)K(s)=diag(w11(s)，w22(s)，…，wnn(s))

(7)

式中：K(s)=(kij(s))∈Rn×n为解耦矩阵，且当i=j时，kij(s)=1。

但对于图1所示的传统解耦结构是无法实时解算系数矩阵A、B、C、D的，因此不能得到实时的前馈补偿，只能离线辨识系数矩阵A、B、C、D再求解出相应的前馈解耦补偿加入到解耦结构，这种传统的解耦结构应用在航空动力装置是受限的，无法适应航空动力装置复杂的工况点变化过程。

图1 传统解耦结构框图

本文所采用的在线前馈补偿的解耦结构，如图2所示，在航空动力装置进行多对回路系统控制时，以简单的传统解耦结构为基础，加入的机载LPV模型根据系统实时的输入和状态可实时解算出系统的系数矩阵A、B、C、D以此得到解耦对象传递函数，利用RGA方法对耦合系统的耦合程度进行在线判断后，对于耦合严重的将使用在线求解的前馈解耦补偿器，以解耦网络去减弱或消除各回路间的关联性达到解耦的目的。如不满足解耦条件，系统的前馈补偿结构将会失效，则系统将无需进行解耦。对于航空动力装置，该解耦结构能够适应其复杂的工况。

图2 在线前馈解耦结构框图

4 实例验证

以一个两输入两输出的电力驱动的变距螺旋桨的动力装置(Variable Pitch Electric Power Plant，VPEPP)为被控对象，该动力装置可用于四旋翼无人机完成机动飞行[17]和农业植保，也可作为长航时飞行器的动力装置，能有效提高其飞行效率。对于这样一种存在耦合多输入多输出的动力装置，为了提高控制品质，将采用上述基于机载LPV模型的在线解耦方法和PID控制器对其进行在线解耦控制，结构框图如图3所示。

图3 VPEPP的在线解耦框图

在图3中，若以占空比主控轴功率，以桨叶角主控拉力，根据电力驱动的变距螺旋桨动力装置的非线性数学模型式(8)可以看出，输出量轴功率和拉力都和转速有关，这使得无论是轴功率或者是拉力发生变化都会影响到转速，从而产生相互干扰的耦合作用，本文将以式(8)作为动力装置以仿真来验证解耦效果。

(8)

式中：两输入量分别是占空比δ和桨叶角β，两输出量分别为轴功率Ns和拉力Lf，角速度ω为状态量。

首先，对于图3的在线解耦控制应获得式(8)的机载LPV模型。在稳态点附近进行小偏差线性化可得到该系统的状态空间方程，如式(9)。

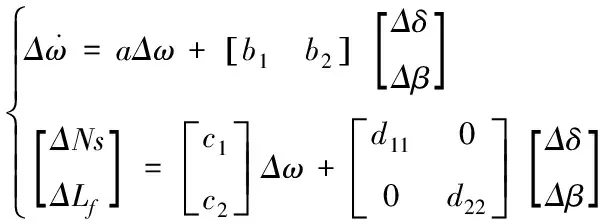
(9)

式中：a、b1、b2、c1、c2、d11、d22是局部线性模型的系数。

之后，根据10组稳态点附近所得到的局部线性模型的系数，以状态量转速ω作为调度变量，对系数矩阵进行拟合可得到电力驱动的变距螺旋桨动力装置的LPV模型的变参数矩阵，如图4所示，以此可得LPV模型，如式(10)。

图4 LPV模型系统矩阵的拟合

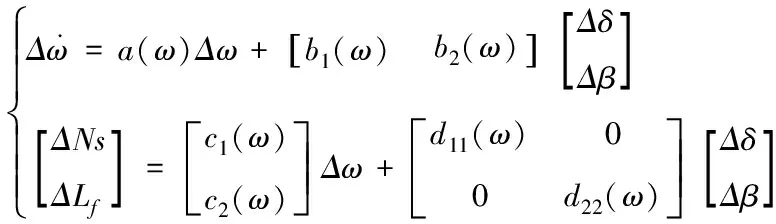
(10)

以MATLAB/Simulink建立LPV的仿真模型，仿真结果如图5所示。

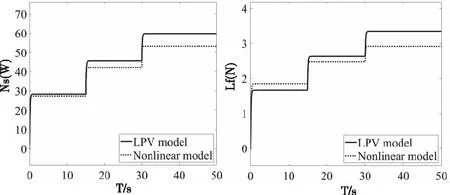
图5 LPV的仿真结果

在图3中，根据所得的LPV模型可得到与动力装置相同输入和对应工况下的各系统矩阵的参数值：a、b1、b2、c1、c2、d11、d22，之后以式(6)可得系统的传递函数矩阵，如式(11)。

(11)

以式(6)计算得式(12)，根据相对增益判据来判断这一两输入两输出系统的耦合程度。

(12)

如式(12)满足RGA判据则需进行解耦，可根据式(7)以不变性原理使得GD(s)的非主对角元素为零，可求解前馈补偿解耦的传递函数，如式(13)，求解结果为式(14)。

(13)

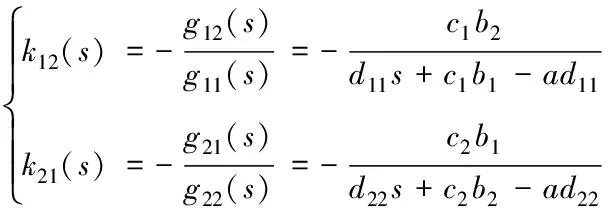
(14)

最后根据以上过程在MATLAB/Simulink上搭建电力驱动的变距螺旋桨动力装置的在线解耦控制系统的模型，并进行仿真验证，如图6所示。

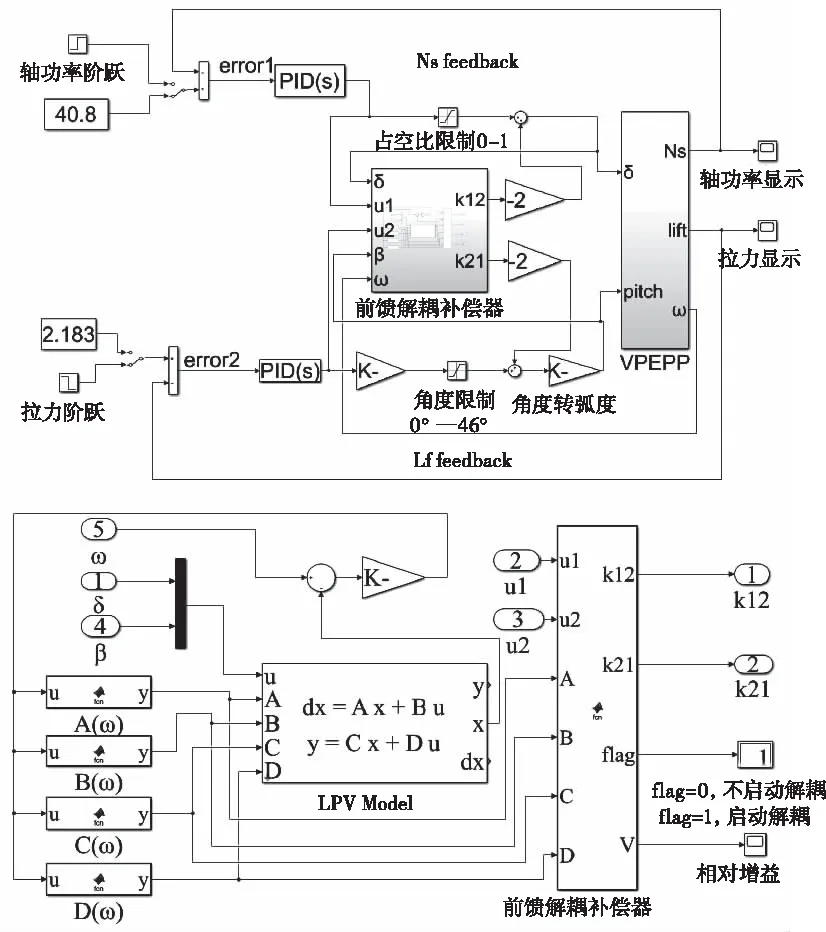
图6 VPEPP 在线解耦控制系统的仿真模型(轴功率—拉力双回路控制)

为了保证控制系统的稳定性，对以上PID控制器的参数进行离线整定，之后以电力驱动的变距螺旋桨动力装置的三个工况来进行仿真验证。在工况1下，根据变距电动力装置的LPV模型可求出其线性模型中A、B、C、D的各系数矩阵的参数，如图7所示。

图7 矩阵参数在线解算结果

将各矩阵参数代入系统传递函数矩阵，之后可解算出耦合系统的相对增益，如图8所示。在图8中该耦合系统的相对增益λ11、λ12、λ21、λ22均在0.3～0.7之间，满足相对增益判据，说明在工况1条件下，此系统是一个强耦合系统，则需进行解耦。此时根据辨识出的各矩阵参数以前馈解耦法解算出系统解耦的前馈补偿传递函数k12(s)和k21(s)进行解耦，解耦效果如图9所示。其余的两个工况点按以上仿真过程，解耦效果如图10和图11所示。

图8 工况1解耦过程的相对增益

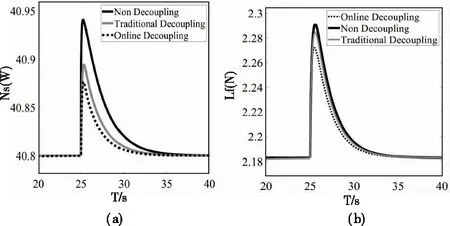
图9 工况1解耦效果

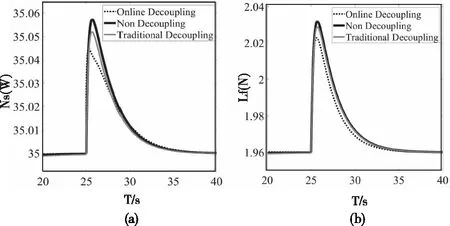
图10 工况2解耦效果

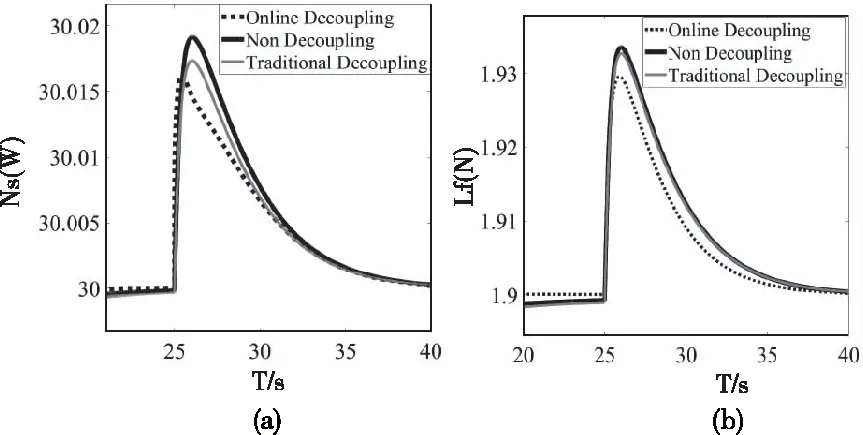
图11 工况3解耦效果

从图9，10，11中(a)的情况是输入的轴功率Ns不变时，输入的拉力Lf产生阶跃，由于回路间的耦合干扰作用使得轴功率的输出端产生了突跃偏离了给定值；图9，10，11中(b)的情况是输入的拉力Lf不变时，输入的Ns产生阶跃，由于回路间的耦合干扰作用使得拉力的输出端产生了突跃偏离了给定值。从图9，10，11中可看出使用在线解耦方法比传统解耦的突跃程度要小，改善了解耦效果。

如果将上述双回路控制其中的拉力Lf控制回路改为转速ω控制回路，则变成轴功率-转速双回路控制，则相应的LPV模型变为式(15)

(15)

根据该模型的特性发现轴功率回路的响应比转速控制回路快，则可以考虑对该双回路控制系统进行部分解耦。因为对于两个响应速度不一样的控制通道而言，响应快的被控参数受响应慢的参数通道的影响小可以不考虑耦合作用；而响应慢的被控参数受响应快的参数通道耦合影响大，需要对响应慢的参数通道进行解耦[18]，所以对于轴功率-转速控制回路而言应对转速控制回路进行部分解耦。以图3的在线解耦方法进行对转速控制回路的解耦，在Simulink中构建仿真模型如图12所示。在仿真中对轴功率进行阶跃，而使转速保持不变，在四个工况点下对转速回路的在线解耦效果进行验证，并与传统的解耦效果进行对比，结果如图13所示。

图12 VPEPP 在线解耦控制系统的仿真模型(轴功率—转速双回路控制)

根据图13中的解耦效果来看，轴功率的阶跃会对转速造成很大的干扰，虽然这种干扰会随着时间的推移逐渐被控制器抑制，但调节时间过长，而采用本文提出的在线解耦方法后，转速回路的受到的干扰在解耦补偿的作用下立即将轴功率回路的耦合影响基本消除，并在多个工况点下解耦效果都很好，且对比传统的解耦结构，该在线解耦结构反映出对工况点的变化很好的适应性。

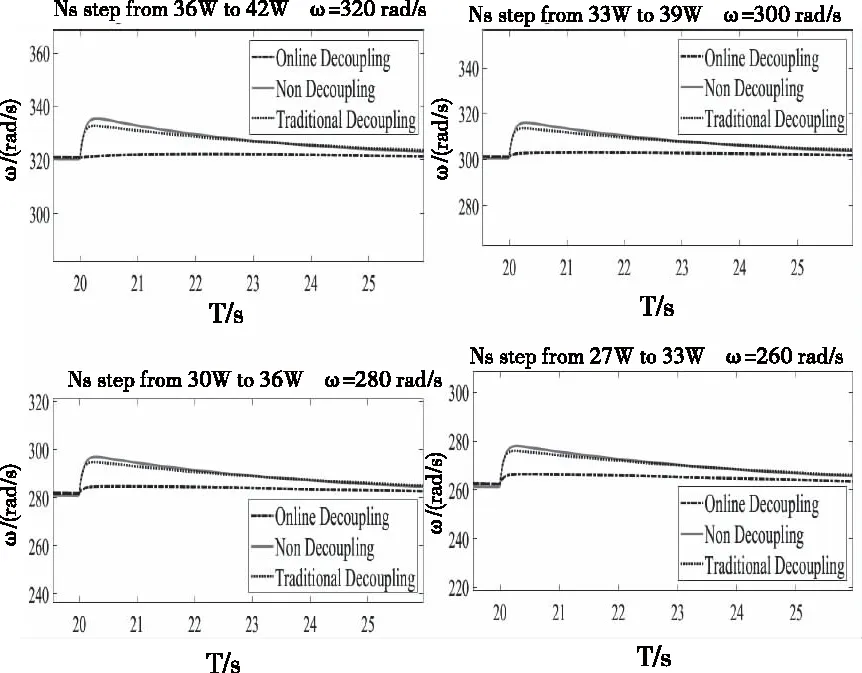
图13 转速控制回路解耦效果

5 结论

本文针对航空动力装置这一典型的多变量耦合系统，保留了传统的PID控制方法和前馈补偿优异控制性能的同时，引入了机载LPV模型在线直接解算出系统的矩阵参数，避免使用计算量大、解算时间长且复杂的在线辨识算法去辨识被控对象的模型。以被控对象的参数实时解算、解耦和控制结合起来实现非线性航空动力装置耦合系统在工况点附近的线性模型参数未知时的在线解耦控制。从仿真结果来看，提出的在线解耦方法比传统的静态解耦方法对被控对象的适应性要更强，能够在线解算出前馈解耦补偿的传递函数，改善了回路之间的耦合关系，提高了解耦效率，为实现多变量解耦控制提供了一种新的思路。