改进粒子群算法优化回声状态网络的电力需求预测研究*

王 林，王燕丽，安泽远

(华中科技大学管理学院，湖北 武汉 430074)

1 引言

电力能源是国家经济发展的重要基础，电力能源的有效利用程度和消费量是衡量人类生产技术和生活水平的重要标志。2019年，由于受到贸易摩擦、逆全球化等不利因素导致的经济增速放缓，以及2018年拉动能源需求的一些一次性因素部分缓解，全球用电量增速下降至1.3%，不到上年增速(2.8%)的一半。2020年，大部分国家受到疫情冲击，全球用电量下降约0.7%。电力需求受诸多相互作用且具有内在复杂性和不规则性因素影响导致的波动变化，对国家或者地区的电力能源安全规划提出了更高的要求，其中预测精度是电力需求预测问题的研究重点。

目前已有许多来自世界各地的研究人员对电力需求预测进行了相关研究，主要预测模型包括统计模型、机器学习和混合模型。Sarkodie[1]使用自回归移动平均模型ARIMA(AutoRegressive Integrated Moving Average model)模型，通过人口和国内生产总值来预测加纳的电力需求；Wang等[2]运用卷积积分优化的灰色多元模型预测中国工业用电能耗；Kialashaki等[3]利用人工神经网络ANN(Artificial Neural Network)预测美国的工业用电需求；Rahman等[4]运用一种新的深度递归神经网络模型预测商业和住宅建筑的电力负荷需求；马煜等[5]通过结合卷积神经网络和支持向量回归的思路，来提取影响电力负荷因素的高维特征。但是，现有能源需求预测模型普遍存在精度有待提高或者操作较复杂等问题，因此寻找高效和精确的新型预测方法成为了研究的焦点。

Jaeger等[6]提出了回声状态网络ESN(Echo State Network)。与传统的人工神经网络相比，ESN使用了动态递归网络储备池，在解决非线性问题时，能够克服传统操作存在的计算复杂、耗时长，以及容易陷入局部最优等问题。ESN已被广泛应用于各领域的预测问题。众多研究人员还对ESN进行了改进，如张亚丽等[7]采用改进的局部均值分解方法，与回声状态网络相结合，以提高预测精度；Li等[8]提出了一种基于先验数据的多层储备池生成算法；Hu等[9]将深度学习框架引入基本的ESN中，结合回声状态网络强大的非线性时间序列建模能力和深度学习框架的高效学习能力，提出了DeepESN，通过多个算例验证了其性能良好。也有研究人员使用启发式算法对ESN进行参数优化，获得了良好的效果，例如Wang等[10]运用差分进化算法优化回声状态网络的储备池关键参数。本文拟采用改进的群体智能优化方法对ESN进行改进。

Eberhart等[11]提出的粒子群优化PSO(Particle Swarm Optimization)算法是一种容易实现但性能强大的随机优化技术，能够用于解决复杂的连续或组合非线性问题。但是，PSO算法自身存在收敛精度低、不稳定、容易陷入局部最优解等缺点。朱小明等[12]通过对PSO算法进行理论分析，指出算法容易过早收敛的主要原因是种群多样性的缺失。为此研究人员近年来对PSO算法进行了大量研究，如Zhang等[13]提出了一种基于终端交叉和转向的分布式PSO算法，Rehman等[14]提出了一种改进的量子启发式PSO算法。

本文首先引入自适应算子对PSO算法进行改进，以提高其探索当前空间和开发未知空间之间的平衡性；同时，采用非线性函数来构建ESN储备池内部状态之间的非线性关系；接着利用改进的粒子群优化APSO(Adaptive Particle Swarm Optimization)算法对非线性回声状态网络NESN(Nonlinear Echo State Network)的关键参数进行优化，以构建APSO-NESN组合预测模型；最后运用该模型进行能源需求预测，以期为一个国家或地区的相关能源决策提供可靠的辅助支持。本文为ESN在能源需求预测上的应用提供了新的研究思路，为相关经济活动管理提供了有益的管理借鉴。

2 粒子群优化算法及其改进

2.1 粒子群优化算法原理

PSO算法是基于群体迭代模式的启发式算法，它在搜索过程中通过个体间的交互行为来寻找最优值，具有收敛速度快、全局搜索能力强和易于实现等优点。

2.2 粒子群优化算法的数学模型

首先初始化粒子群，规模为m，在空间坐标系连续的情况下，第i个粒子的当前位置为xi=(xi1,xi2,…,xid)，历史最优位置为Pi=(Pi1,Pi2,…,Pid)，当前速度为vi=(vi1,vi2,…,vid)。所有粒子中的最好位置可以表示为Pg=(Pg1,Pg2,…,Pgd)。其中,i=1,2,…,m;d为空间维度。

粒子群中每个粒子第j维在t+1时刻的速度更新如式(1)所示：

(1)

其中,c1和c2均为非负的学习因子，保证了粒子尽可能往个体最优和全局最优的地方移动;ω表示惯性权重,Shi等[15]通过仿真实验得出，通常情况下ω在[0.9,1.2]。非负常数c1和c2通常都设置为2，rand()表示[0,1]的随机数。

在更新过程中，通过设置Vmax来控制速度更新范围，避免因速度过大而错过最优位置。粒子群中每个粒子第j维在t+1时刻的位置更新如式(2)所示:

(2)

2.3 粒子群优化算法的改进

适应度计算由式(3)所示:

(3)

其中,yk是利用当前粒子的位置信息输出的预测值，Wk是已确定的实际值，n表示待比较的y和W的长度。

若输出的预测值和实际值偏差很大，该粒子的适应度函数值也会很大，则此时粒子处于一个较差的解空间，粒子需要以一个较大的速度尽快离开该空间，以避免消耗过多的迭代次数；相反，若一个粒子的适应度函数值很小而更新速度很大，那么可能会导致粒子在较优的解空间中不能进行充分的探索。在标准PSO算法中，由于惯性权重ω和学习因子c1、c2是固定的，搜索当前最优空间和探索新空间这2种操作无法平衡，PSO算法的效率和优化能力就会受到影响。

为了解决上述问题，本文引入了自适应非线性惯性权重和学习因子。本文将惯性权重ω的赋值方法由初始设定改成了如式(4)所示的自适应非线性惯性权重:

(4)

其中,mapetarget表示设定的目标适应度，ωstandard表示设定的初始标准惯性权重,objvaluezbest表示当前粒子群最优的适应度。

惯性权重ω由固定值转化为了一个与设定的惯性权重、设定的目标适应度和当前的适应度相关的值。随着粒子的迭代计算，当前粒子群最优适应度逐渐降低，表示粒子不断接近最优解；而惯性权重也随之不断减小，这使得粒子的更新速度降低，保证了粒子能在较优的解空间中进行更为充分的搜索。可见，惯性权重能够随着当前全局最优适应度与目标适应度之间的差距变化发生相应变化，从而平衡了当前最优空间和新空间的搜索，成为一种“动态”的学习过程，提高了算法效率。

学习因子c1和c2的赋值方法由初始设定改成了如式(5)所示的自适应非线性学习因子，同样也是为了获得“动态学习”能力。

(5)

引入了自适应非线性惯性权重和学习因子的PSO算法，本文称之为自适应粒子群优化算法——APSO算法。

3 回声状态网络及其改进

3.1 标准回声状态网络

ESN是一种特殊的递归神经网络，具有训练过程简单、收敛速度快和处理非线性问题能力强等优点，适合处理非平稳的时间序列数据。其标准的组成部分为具有K个神经元的输入层、包含N个内部神经元的储备池层和具有L个神经元的输出层。标准的ESN结构如图1所示，图中黑色实线表示在网络初始化时随机生成但在训练过程中保持不变的连接权重；灰色虚线表示在ESN中需要训练的储备池输出权重；灰色实线表示输出层与储备池的反馈连接。

本文使用最小二乘法LSM(Least Squares Method)来获得输出连接权重。为了使ESN网络具有短时记忆功能，必须使动态储备池保持1%～5%的稀疏度，且其权值矩阵W的谱半径小于1[16]。

Figure 1 Structure of standard ESN图1 标准ESN结构图

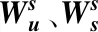
与此同时，ESN在t时刻的储备池内部状态s(t)和输出o(t)的更新公式分别如式(6)和式(7)所示：

(6)

(7)

其中，f(·)表示储备池内部状态的激活函数;fout(·)表示输出状态的激活函数，本文均选择了tanh函数作为激活函数；储备池内部状态s(t)在网络中初始化为零向量。

3.2 非线性回声状态网络

ESN的特点是具有回声状态属性的储备池，其隐藏层神经元具有大量、随机和稀疏组合的特性。标准ESN储备池内部状态的关系是线性的，本文采用非线性函数来构建储备池内部状态的非线性关系，将改进后的ESN称为非线性回声状态网络NESN。NESN的结构如图2所示，与ESN相比，NESN增加了M=p×q个单元的读出层,其中，p为NESN储备池内部神经元的数量，q为构建储备池内部状态之间关系的非线性函数的阶数。NESN在使用更少储备池内部神经元的情况下，进一步提升了储备池的非线性动态存储能力，进而提高了处理复杂的非线性问题的能力。

Figure 2 Structure of NESN图2 NESN结构图

NESN在t时刻的输出o(t)的计算公式如式(8)所示，式(9)和式(10)是读出层内部神经元，表示它是由储备池内部的神经元非线性组合而来。

(8)

(9)

s(t)=[s1(t),s2(t),…，sq(t)]T

(10)

4 组合预测模型APSO-NESN

4.1 APSO-NESN基本原理

本文将APSO与NESN相结合，构建了一种新的组合预测模型APSO-NESN，其主要思路是运用APSO算法来对NESN的储备池稀疏度和谱半径进行参数寻优，同时优化输出连接权重的计算方式。与经典的ESN相比，该组合预测模型利用了APSO算法的全局搜索能力来替代传统的参数设定模式，同时该模型还具有NESN所特有的优点。实验结果表明，本文提出的APSO-NESN组合预测模型不仅能够减少储备池内部神经元的数量和计算负荷，还获得了更好的学习能力和更高的运算效率。

4.2 APSO-NESN算法步骤

APSO-NESN主要分为2个阶段，在第1个阶段中，该组合模型运用APSO算法对NESN的参数进行寻优，APSO算法的决策变量由储备池稀疏度、谱半径和输出连接权重组成，其适应度函数值为将每个粒子的位置变量xi代入NESN中返回的对应预测误差值；在第2个阶段中，该组合模型将在第1阶段中APSO算法获得的优秀个体解码作为参数值来初始化NESN，并进行预测。具体流程如图3所示，详细描述如下所示：

(1)读取数据。对输入数据进行归一化预处理，并将数据划分为训练集和测试集，训练集用于APSO算法优化储备池稀疏度和谱半径，以及在线训练得到输出连接权重。

(2)NESN参数设置及初始化。设置输入神经元数量K、储备池内部神经元数量p、输出神经元数量L和非线性函数的阶数q等参数，并初始化除了输出连接权重矩阵外的其它连接权重矩阵，选择双曲正切函数为储备池内部神经元激活函数。

(3)APSO算法参数设置及初始化。设置种群规模、最大迭代次数、空间维度、最大和最小速度、标准惯性权重和目标适应度等参数，并生成初始种群，按式(3)计算初始种群中各粒子的适应度函数值，将其最优适应度值作为初始个体最优适应度值和全局适应度值。本文APSO算法的适应度函数值为将每个粒子的位置变量xi对应的参数值代入NESN模型中进行预测返回的预测误差值。

Figure 3 Flow chart of APSO-NESN algorithm图3 APSO-NESN算法流程图

(4)对APSO算法的初始种群进行自适应惯性权重和学习因子更新、速度更新与判断及位置更新操作，以获得新一代种群；计算种群中各粒子的适应度函数值，对全局最优个体的位置和适应度进行更新并记录。重复操作此步骤直至达到APSO算法的最大迭代次数，返回全局最优个体的位置。

(5)判断NESN是否达到运行的终止条件(达到设置的最大运行次数)，如果达到，则停止迭代过程，输出预测模型历史迭代运算中最小的预测误差及测试样本对应的预测值；如果未达到运行的终止条件，则继续执行下一步。

(6)将APSO算法优化得到的全局最优个体解码为NESN对应的参数，并将优化得到的储备池稀疏度、谱半径和输出连接权重代入到NESN中，生成非线性回声状态网络；然后输入测试集进行预测，计算模型对测试样本的预测误差。

(7)更新NESN模型历史迭代运算中最小的预测误差，并将算法当前的迭代计数增加1，继续执行第(5)步，判断算法是否达到终止条件。

5 实例仿真和结果分析

为了检验组合预测模型APSO-NESN在电力需求预测上的应用效果，本文选择了2组真实的能源需求数据，并综合运用多种误差评价指标，包括平均绝对百分比误差MAPE(Mean Absolute Percentage Error)、均方根误差RMSE(Root Mean Square Error)和平均绝对误差MAE(Mean Absolute Error)，确保预测模型效果评价的全面性与客观性。上述指标的计算如式(11)～式(13)所示：

(11)

(12)

(13)

5.1 美国电力需求预测

5.1.1 实验数据及数据集划分

为了验证APSO-NESN在电力需求预测方面的效果，本节仿真实验使用的数据与文献[17-19]中的相同。数据集的时间跨度为1967年～2009年，共包含了43年的电力需求EEC(Electrical Energy Consumption)、国内生产总值GDP(Gross Domestic Produce)、人口POP(PoPulation)、进口额IMP(IMPort)和出口额EXP(EXPort)，如图4所示。

Figure 4 Electricity demand of USA and its four influencing factors related data from 1967 to 2009图4 美国1967年～2009年电力需求及其4个影响因素相关数据

5.1.2 参数设置与实验结果分析

本文仿真实验是在Matlab R2009b的编程环境下实现的，在充分考虑了文献[9-11,20]中的经验和多次实验后，APSO-NESN、DeepESN和DE-ESN的参数设置如表1所示。

模型参数设置完成后，将测试样本作为预测模型的输入进行预测。使用APSO算法优化NESN迭代过程的误差梯度走势如图5所示。优化得到的储备池稀疏度SD=0.2953和谱半径SR=0.812，优化结束后预测模型得到的测试样本预测值与实际值的对比如图6所示。

Table 1 Parameter settings of APSO-NESN,DeepESN and DE-ESN (USA) 表1 APSO-NESN,DeepESN和DE-ESN 3种优化算法的参数设置(美国)

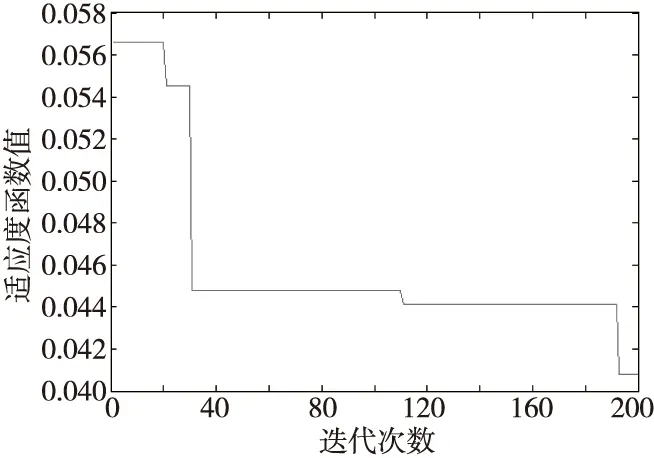
Figure 5 Error gradient trend of APSO-NESN (USA)图5 APSO-NESN误差梯度走势图(美国)

Figure 6 Comparison between predicted value and actual value of APSO-NESN (USA)图6 APSO-NESN预测值与实际值对比图(美国)

APSO-NESN、文献[9,10]中的模型及其它研究[17 - 19]中的模型的预测效果对比如表2所示。其中,DeepESN是一种采用堆叠层次结构的ESN新模型[9]，DE-ESN是一种基于ESN的混合预测模型[10]，这2种模型在类似预测问题上表现出了良好的综合性能。故除了APSO-NESN，这2种模型在本文中同样也被用作对比模型，以期得到客观的对比数据。SFL-QR、IPSO-QR、SFL-ANN来自于文献[17]，GD-ANN、PSO-ANN、IPSO-ANN来自于文献[18]，ADE-BPNN来自于文献[19]，相应的预测结果都是从文献[19]中直接获取的。文献[17]在运用GDP、POP、IMP和EXP4种社会经济因素对美国电力需求进行预测的同时，提出了将对电力需求预测产生积极影响的需求方管理DSM(DemandSideManagement)作为补充因素考虑进来，运用上述4个社会经济因素和DSM作为预测模型的自变量，将预测结果与未考虑DSM情况下的预测结果进行比较，如图2所示。数据显示,对比模型中最低的MAPE为ADE-BPNN的0.34%，而APSO-NESN的MAPE达到了0.31%，效果更好。

Figure 7 Industrial electricity consumption of Guangdong and its eight influencing factors related data from Jan.2016 to Oct.2019图7 广东省2016年1月～2019年10月工业用电量及其8个影响因素相关数据

Table 2 Comparison of MAPE between APSO-NESN and other models (USA)表2 APSO-NESN与其他对比模型的MAPE对比(美国)

5.2 广东工业用电消耗量预测

5.2.1 输入变量特征选择与数据集划分

本节仿真实验将APSO-NESN用于广东省月度工业用电消耗量预测。数据集包含了2016年1月至2019年10月共46个月的工业用电量IEC(Industrial Electricity Consumption)和影响IEC的8个因素，即出口额Export、进口额Import、工业出口交货值IEDV(Industrial Export Delivery Value)、工业销售产值ISV(Industrial Sales Value)、工业增加值IAV(Industrial Addition Value)、工业生产者购进价格指数PPI-buy(Industrial Producer Purchase Price Index)、工业生产者出厂价格指数PPI-sale(Industrial Producer Price Index)和工业企业利润总额IEP(Industrial Enterprises Profits)，如图7所示。

研究表明预测模型的效果受输入数据质量影响较大，因此，对输入变量进行选择是实现更准确预测、更好解释和确定关键变量进而对问题进行更深入分析的重要步骤。梯度提升决策树GBDT(Gradient Boosting Decision Tree)是嵌入式变量选择方法boosting中的一种，属于基于树的集成算法，使用决策树作为学习器，对模型性能影响较小，同时模型训练结束后可以输出特征的相对重要度，以获取影响预测结果的关键因素。

GBDT衡量特征相对重要度的方式是通过计算所有非叶子节点在分裂时不纯度的减少之和。不纯度的减少值表示该节点此次分裂的收益值，因此节点分裂时收益越大，其相对重要度越高。本节仿真实验中采用的是Friedman[21]提出的GBDT中计算特征相对重要度的方法。GBDT中构建的树都是二叉树，特征α在单棵树中的相对重要度计算如式(14)所示，特征α的全局相对重要度通过特征α在单棵树中相对重要度的平均值来衡量，如式(15)所示:

(14)

(15)

本文实验中基于GBDT的特征选择是在Python 3.6的环境下编程实现的。首先将数据集划分为GBDT模型的训练集、验证集和测试集，其中训练集有28个样本，验证集有8个样本，测试集有10个样本。将划分完成的数据集输入到基于GBDT进行特征选择的模型中，在训练过程中根据式(14)和式(15)来计算各个特征的相对重要度，最后输出特征的相对重要度。

影响IEC的8个因素对应的特征的相对重要度及其排序如图8所示。去掉相对重要度最低的Import，将剩余的7个影响因素及IEC作为新的数据集，再次运用GBDT模型对新样本进行特征选择，以期对特征变量进行更为有效的选择，得到的新样本中7个因素对应的特征相对重要度及其排序如图9所示。本文又去掉了相对重要度最低的PPI-sale，然后将剩余的6个影响因素，即IEP、PPI-buy、Export、IEDV、IAV和ISV作为预测模型的输入变量。将2016年1月～2018年12月的36个数据设置为训练集，2019年1月～2019年10月的10个数据设置为测试集。先对所有的数据进行归一化预处理，使每个变量的取值都在[0,1]。

Figure 8 Relative importance of features based on GBDT (8 features)图8 基于GBDT的特征相对重要度(8个特征)

Figure 9 Relative importance of features based on GBDT (7 features)图9 基于GBDT的特征相对重要度(7个特征)

5.2.2 参数设置与实验结果分析

本节实验的运行环境与5.1节的相同。ARIMA预测模型的参数设置为ARIMA(1,1,1)。多元线性回归MLR(Multiple Linear Regression)预测模型使用的是SPSS软件中默认的参数。DeepESN和DE-ESN的参数设置中除了调整输入神经元数量外，其他参数设置均不做改变。APSO-NESN和PSO-NESN参数设置如表3所示。

Table 3 Optimization algorithm parameter settings of APSO-NESN and PSO-NESN (Guangdong)表3 APSO-NESN和PSO-NESN优化算法参数设置(广东)

参数设置完成后，将测试样本作为预测模型的输入进行预测。APSO和PSO优化NESN的迭代过程中误差梯度走势分别如图10和图11所示;APSO优化NESN得到的储备池稀疏度和谱半径，优化结束后预测模型得到的测试样本预测值与实际值的对比如图12所示；PSO优化NESN得到的储备池稀疏度和谱半径，优化结束后预测模型得到的测试样本预测值与实际值的对比如图13所示。

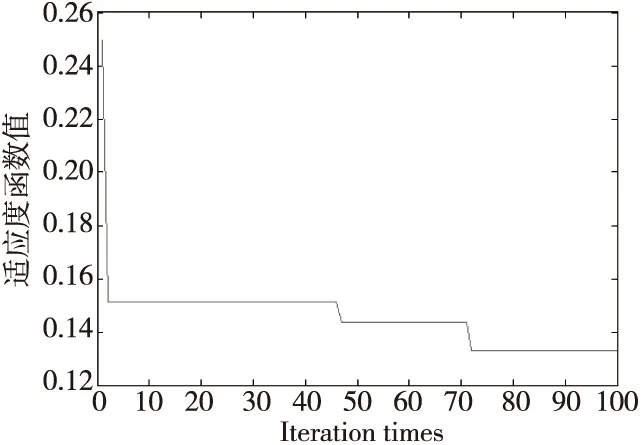
Figure 10 Error gradient trend of APSO-NESN (Guangdong)图10 APSO优化NESN误差梯度走势图(广东)

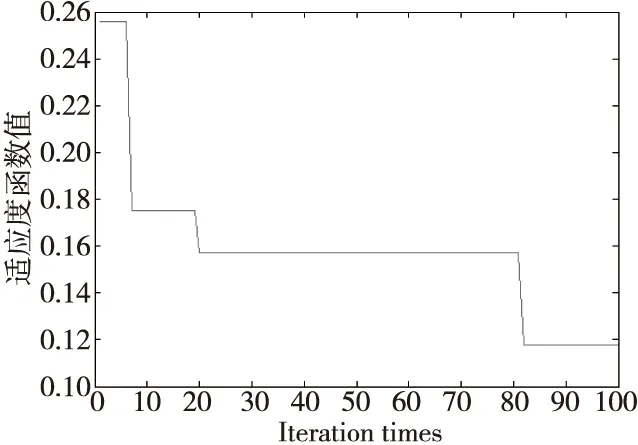
Figure 11 Error gradient trend of PSO-NESN (Guangdong)图11 PSO优化NESN误差梯度走势图(广东)

Figure 12 Comparison between predicted value and actual value of APSO-NESN(Guangdong)图12 APSO-NESN预测值与实际值对比图 (广东)

Figure 13 Comparison between value and actual value of PSO-NESN predicted (Guangdong)图13 PSO-NESN预测值与实际值对比图 (广东)

APSO-NESN的预测效果与ARIMA、MLR、ESN、DE-ESN、DeepESN、NESN和PSO-NESN共7种对比模型的预测效果如表4所示。其中，ARIMA是一种常用的时间序列预测模型；MLR采用了分段拟合策略，是一种广为采用的模型；除了DE-ESN和DeepESN，本文还将APSO-NESN中嵌入的ESN、NESN和PSO-NESN作为比较模型来分析所提出模型单个组成部分的影响。实验结果显示，APSO-NESN的MAPE为3.44%、RMSE为13.84、MAE为11.34，较对比模型在3种预测精度衡量指标上均具有明显优势。APSO-NESN预测结果的MAPE比ESN的下降了33.85%，比基本的NESN的下降了32.55%，比PSO-NESN的下降了15.27%，从中可以看出APSO提高了NESN的预测性能。此外，相比ARIMA和MLR，APSO-NESN的预测效果有大幅的提升。实验结果表明,APSO-NESN在电力需求预测方面是有效的，可以作为一个具有竞争力的替代方法。

Table 4 Comparison of MAPE between APSO-NESN and other prediction models(Guangdong)表4 APSO-NESN与其他预测模型结果及对比(广东)

6 结束语

本文首先引入自适应算子对标准PSO算法的惯性权重和学习因子进行改进，并采用非线性函数来构建ESN储备池内部状态的非线性关系；然后利用APSO算法对NESN的关键参数进行优化，以构建APSO-NESN组合预测模型，拓展了算法的应用领域，为ESN的应用提供了新的思路。在实验中，本文将APSO-NESN用来预测美国电力需求和广东工业用电消耗量。在美国电力需求预测中，APSO-NESN的MAPE达到了0.31%，优于SFL-QR、IPSO-QR、SFL-ANN、IPSO-ANN、GD-ANN、PSO-ANN、ADE-BPNN、DE-ESN和DeepESN预测模型。在广东工业用电消耗量预测中，APSO-NESN的MAPE为3.44%,RMSE为13.84,MAE为11.34，比ARIMA、MLR、ESN、DE-ESN、DeepESN、NESN和PSO-NESN预测模型效果更好。实验结果表明，引入自适应算子和非线性函数的APSO-NSN组合预测模型在收敛速度和预测精度上表现更优，验证了模型的有效性。未来可通过拓展储备池拓扑结构优化的方式来提高APSO-NESN模型的预测效果，并尝试使用多种深度学习方法(如XGBoost)更有效地选择适合能源需求预测的信息。