抑制电压暂降的线路改造方案多目标优化

胡翀，甄超，徐斌，计长安，季坤

（国网安徽省电力公司电力科学研究院，合肥 230022）

0 引言

电力系统正常运行中难以避免的电压暂降与高技术电力用户间的矛盾已经成为电网和用户最关注的问题[1]。从源、网、荷侧采取协同措施是解决问题的根本出路。其中电网侧线路改造是电网侧重要措施之一，研究线路改造方案多目标优化方法具有重要理论价值和现实意义。

国内外对电压暂降抑制的研究主要集中于三方面。第一，电网侧抑制电压暂降水平；第二，用户侧提升设备耐受能力；第三，电网侧或用户侧加装补偿装置。电网改造和加装补偿装置是主要措施，后者主要集中于用户侧，如：加装DVR、UPS 等[2-3]。文献[4]提出一种抑制电压暂降的网络重构方法；文献[5]提出一种故障限流器配置和投切策略，但只能抑制安装线路故障引起的电压暂降；文献[6]提出一种保护定值优化方法，但实用性还需验证。导致电压暂降的主要原因是电网线路故障，降低线路故障率是有效措施。但不同改造措施的改造效果不同，改造类型和实施位置不同，所需成本、收益和抑制效果不同，尚需研究线路改造方案多目标优化方法。

现有电网和线路改造方案优化中，大多仅考虑了电压暂降幅值，优化过程中把电压暂降约束转化为经济损失[7]，主观性强，实用性不足。本文提出一种多目标优化方法，从不同改造方案的抑制机理出发，以实施位置、类型为优化变量，以电压暂降严重程度、改造成本和预期收益为目标，建立多目标优化模型，采用多目标进化算法SPEA2+SDE 进行优化求解，并用IEEE 30 系统验证本文方法的有效性和实用性。

1 线路故障引起的电压暂降抑制机理

1.1 线路随机故障引起的电压暂降评估

采用蒙特卡洛法进行电压暂降随机估计，以故障参数作为随机变量，建立故障随机模型，对故障进行随机采样，模型如下：

1）线路故障随机变量x1。

线路故障概率与故障率、线路长度有关，线路i的故障概率Pi为

式中：λi为线路i的故障率；li为故障线路长度；n为线路总数。

线路故障概率可用随机数x1的分布表示为

式中，x1服从[0～1]均匀分布。

2）故障点位置随机变量x2。

确定故障线路后还需明确线路上故障的具体位置。假设线路上任意位置故障的概率相同，即故障点位置可用服从[0～1]均匀分布的随机数x2表示。

3）故障类型随机变量x3。

故障类型可分为三相短路、两相短路、两相接地和单相接地共4 种类型，分别用P1～P4表示其概率，并设x3为故障类型随机数，服从（0，1）均匀分布。设x3概率分布F3=1，2，3，4 分别表示三相短路、两相短路、两相接地和单相接地。

4）故障清除时间随机变量x4。

电压暂降持续时间取决于短路故障清除时间，在确定采样故障线路、故障点位置后，可根据线路保护配置情况确定主、后备保护动作时间，考虑保护时限特性[9]假设故障清除时间符合以主、后备保护整定值为期望，方差为0.01s 的正态分布，用随机数x4表示。

5）电压暂降评估。

采样确定上述随机变量x1～x4后，采用短路计算法评估电压暂降水平。值得注意的是，若发生上述不对称故障时，需考虑到具体故障类型及暂降传播路径上下游变压器类型来评估电压暂降对用户的影响以更好地优化后续线路改造方案。例如根据变压器不同的绕组连接方式对电压暂降传播的影响，可将其分为3 类：Y-Y 连接且中性点都接地的Ⅰ型变压器、Y-Y 连接一边或两边中性点不接地、D-D 连接及D-Z 连接的Ⅱ型变压器以及Y-D、D-Y及Y-Z 连接的Ⅲ型变压器。可通过变换矩阵来计算不同故障类型引起的暂降经变压器传播对用户的影响[10]。

当采样次数足够大，暂降幅值和持续时间统计误差趋近于0 时，评估结束，用评估结果统计不同节点、不同幅值、不同持续时间的电压暂降频次，完成电压暂降评估。

1.2 线路改造抑制电压暂降的机理

采取线路改造方案抑制电压暂降的机理为：不同原因故障采取不同线路改造方案以降低线路故障率，达到电网抑制电压暂降的目的。线路故障原因有：设备老化、雷击、树害、动物接触、外力破坏及其他因素等[11-12]。

线路总故障率λtotal是各原因故障率之和，公式为

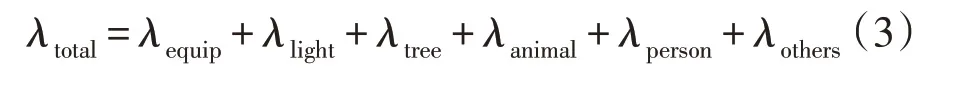
式中，λequip、λlight、λtree、λanimal、λperson、λothers分别为老化、雷击、树害、动物接触、外力破坏和其他因素故障率。

降低不同原因故障率的改造方案不同。统计表明，老化、雷击、树害故障占80%以上[7]，因此，主要考虑这3 种原因的改造方案。其措施分别为电缆改造、安装线路避雷器和树木修剪。

2 抑制电压暂降的线路改造方案多目标优化

2.1 多目标优化模型

不同改造措施减低故障率的效果和成本不同，同一线路不同故障原因可采取一种或多种措施，需对改造实施位置、措施类型进行优化。以抑制电网侧电压暂降为目的的线路改造优化方案，本质上抑制效果与改造成本间的权衡，需同时考虑技术性目标（抑制效果）和经济性目标（改造成本和预期收益），两者有冲突性，且无法公度，因此，分别以电压暂降严重程度和改造投资与收益为目标，建立多目标优化模型。

2.1.1 技术性与经济性目标函数

1）用暂降严重程度刻画的技术性目标函数。

本文以SARFIcurve度量暂降抑制效果[13]。通过考虑敏感设备接入母线的暂降严重程度建立线路改造多目标优化模型的技术性目标函数为

式中，SARFIcurve为暂降严重程度指标，度量暂降抑制效果；w为接入用户侧敏感设备的节点总数。

2）改造成本和预期收益刻画的经济性目标函数。

本文在优化模型中用投资成本和预期收益刻画经济性目标，其函数为

通常线路改造投资成本是线路长度的函数，考虑资金时间价值，年均投资成本为

通过技术性目标函数构造经济性目标中的预期收益函数为

式中：Ci-loss为线路i上未改造前敏感用户受电压暂降影响造成的年经济损失值；fi为线路i上的技术性指标；Δfi为线路改造后的技术性指标差值。

2.1.2 约束条件

优化模型有两类约束：决策变量约束和状态变量约束。决策变量约束分为技术决策变量约束和经济决策变量约束，其中技术决策变量约束是针对改造实施位置和实施类型的约束，公式为

式中，i=1…M，M是备选线路数；N为改造措施类型数，表示不同措施在同一线路上可同时但不重复实施，即同一措施在同一线路上仅可使用一次。

经济决策变量约束是针对改造成本和预期收益的约束，公式为

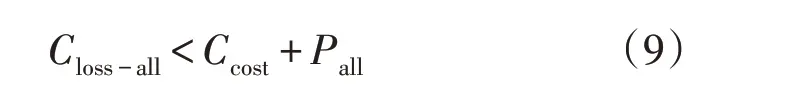
式中，Closs-all为线路不采用任何电压暂降治理技术前所有敏感用户每年遭受电压暂降造成的总损失，Ccost为线路年均投资成本，Pall为线路年均预期收益。

3 求解算法

目标函数中SARFIcurve需通过1.1 节方法确定，无解析表达式，且优化模型为混合整数非线性非凸优化问题，故采用位移密度估计强度帕累托进化算法（SPEA2 with shift-based density estimation）求解[14]。采用SPEA2+SDE 算法求解的流程见图1，具体迭代规则如文献[15]所述，本文不再赘述。

图1 基于SPEA2+SDE的线路改造策略优化流程Fig.1 Flow chart of line modification strategy optimization based on SPEA2+SDE

SPEA2+SDE 算法求解过程中，个体编码方式见图2，个体总长度为M×N，M为待改造线路数量；N为可选的线路改造技术数量。为0-1 变量，表示第j类线路改造技术在候选线路i上实施与否，1 表示实施，0 表示未实施。

图2 个体编码方式Fig.2 Individual coding mode

得到Pareto 最优解集后，若决策者希望获得一最终解，可采用模糊决策法确定最优折衷解[16]。

4 算例分析

4.1 算例描述

以IEEE 30 系统为例，实证分析本文提出的模型和算法的有效性[17]，采用蒙特卡洛法评估采取线路改造措施后的电压暂降严重程度，线路故障率见表1[17]，不同故障原因和比例见表2[18]，线路主、后备保护及其时限特性见表3[9]。

表1 线路故障率Table 1 Fault rate of line

表2 故障原因及类型占比Table 2 Proportion of fault causes and types

表3 线路保护的时限特性Table 3 Time limit characteristic of line protection

现考察变压器不同绕组类型下电压暂降传播对用户的影响，通过设置敏感节点12 变压器类型进行对比分析，见图3，仿真结果见表4。

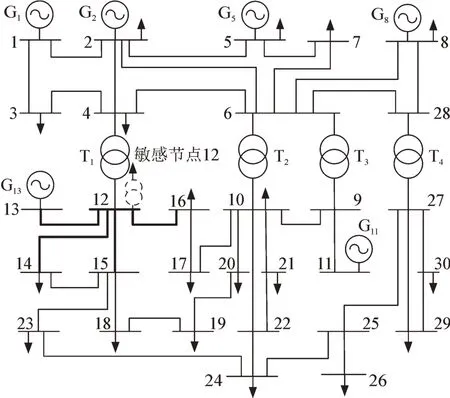
图3 IEEE30节点系统图Fig.3 IEEE 30 node system diagram

表4 变压器类型对用户影响Table 4 Influence of transformer type on customers

通过表4 发现，变压器类型的不同会对电压暂降的传播产生改变进而对敏感用户造成影响，这是因为发生不对称故障时，电压暂降经过Ⅱ型或Ⅲ型变压器前后一二次侧电压暂降幅值会发生变化，进而改变SARFI-SEMI。

改造方案中主要考虑：地下电缆替换架空线、安装线路避雷器和树木修剪3 种改造措施。改造措施对线路故障率的改善效果用故障率改善系数表示，效果与寿命周期见表5[7]，其中，110 kV 线路电缆：YJLW03-64/110 kV-1×400 mm2，单位成本：251.83 万元/km；35kV 电缆：YJV22-26/35 kV-3 ×150 mm2，单位成本：56.99 万元/km[19]；110 kV 线路避雷 器：YH10WX-114/296；35 kV 线 路 避 雷 器：YH5WX-51/134WL，单位成本为分别为65.2 万元/km和16.3 万元/km；110 kV 和35 kV 线路树木修剪成本分别为1.6 万元/km 和0.4 万元/km[7]。

优化算法SPEA2+SDE 参数如表6。

表6 SPEA2+SDE参数Table 6 Parameters of SPEA2+SDE

4.2 线路改造策略多目标优化

4.2.1 不同改造措施治理效果比较

为比较不同线路改造措施的电压暂降抑制效果，首先假设12 节点为敏感负荷接入节点，假设负荷电压暂降耐受能力满足SEMIF47 曲线，每次电压暂降对该节点负荷造成经济损失100 万元/次，电压暂降严重程度指标选取SARFIcurve。选取与12 节点直接相连的线路如图3 所示，分别进行：1）无改造；2）全部采用地下电缆替换架空线；3）全部树木修剪这3 种线路改造策略，计算不改造方案下，12 节点的电压暂降严重程度、成本及收益，结果见表7。

表7 3种线路改造策略下的12号节点电压暂降严重程度、投资成本和预期收益Table 7 Severity of voltage sag、investment cost and expected return of No.12 node under modification strategy of three kinds of lines

可见，不同改造措施抑制电压暂降的效果不同，电缆替换措施比树木修剪措施更有效，但投资较大且收益较低，不满足经济性约束条件；从投资回报率看，树木修剪优于电缆替换。因此，当接入的敏感负荷暂降损失较少时，电缆替换措施不经济，树木修剪更适用，与实际情况吻合。

4.2.2 场景1：单个敏感负荷接入节点

考虑系统单个节点，假设为节点12。为减小问题规模，提高求解速度，假设最多改造线路为5 条。求解所得线路改造方案Pareto 最优解集（Pareto Set）见图4，该解集反映出投资成本与暂降抑制效果冲突，投资成本越高，暂降抑制效果越好，其中预期收益由暂降抑制效果决定，为提高求解速度，不再将其列入待解量。得到Pareto 最优解集后，决策者对暂降抑制效果和投资成本按照预算选择最优方案，见表8。在表8 的Pareto 解中，线路改造方案均对针对距离敏感节点较近的线路进行，与暂降产生机理相符，证明了本文方法的合理性和有效性。

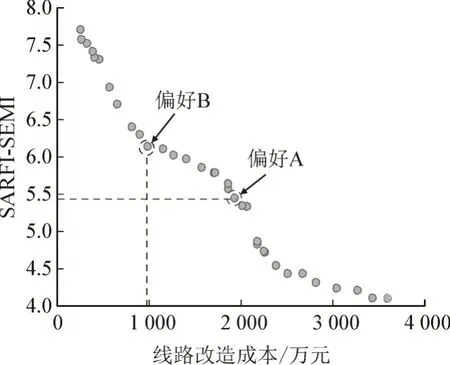
图4 Pareto最优解集（场景1）Fig.4 Pareto solution set（scenario 1）

表8 不同偏好下的最优解Table 8 Optimal solutions under different preferences

4.2.3 场景2：多个敏感负荷接入节点

1）以敏感节点综合电压暂降严重程度为目标（场景A）。

越来越多节点接入敏感负荷的场景下，假设敏感负荷接入点分别为节点12 和16，采用本文模型和算法优化线路改造方案。将多个敏感节点母线SARFIsemi之和作为电压暂降严重程度目标函数，用SPEA2+SDE 算法求解，得最多改造线路数为5 条，Pareto 最优解集见图5。

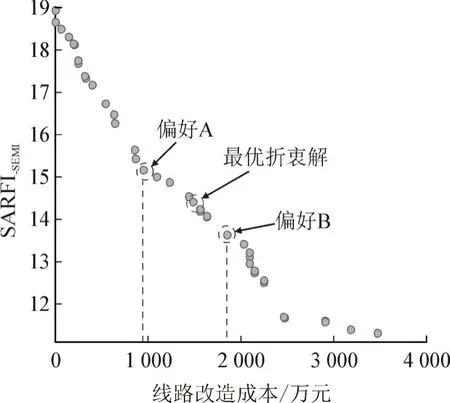
图5 Pareto最优解集（场景A）Fig.5 Pareto solution set（scenario A）

若决策者无投资成本或暂降抑制指标偏好，可采用模糊决策法确定最方案，见表8。若存在投资偏好，假设投资成本分别为1 000 万元（偏好A）和2 000 万元（偏好B），最优解见表9，其中16 号节点治理前暂降频次为10.21 次/年。由不同投资约束下的最优改造方案可知，当投资成本约束为1 000万元时，节点12 和16 的综合暂降抑制指标SARFIsemi为15.12 次/年；当投资成本约束增加到2 000 万元时，节点12 和16 的暂降综合抑制指标SARFIsemi为13.17 次/年，投资越大，抑制效果越好。

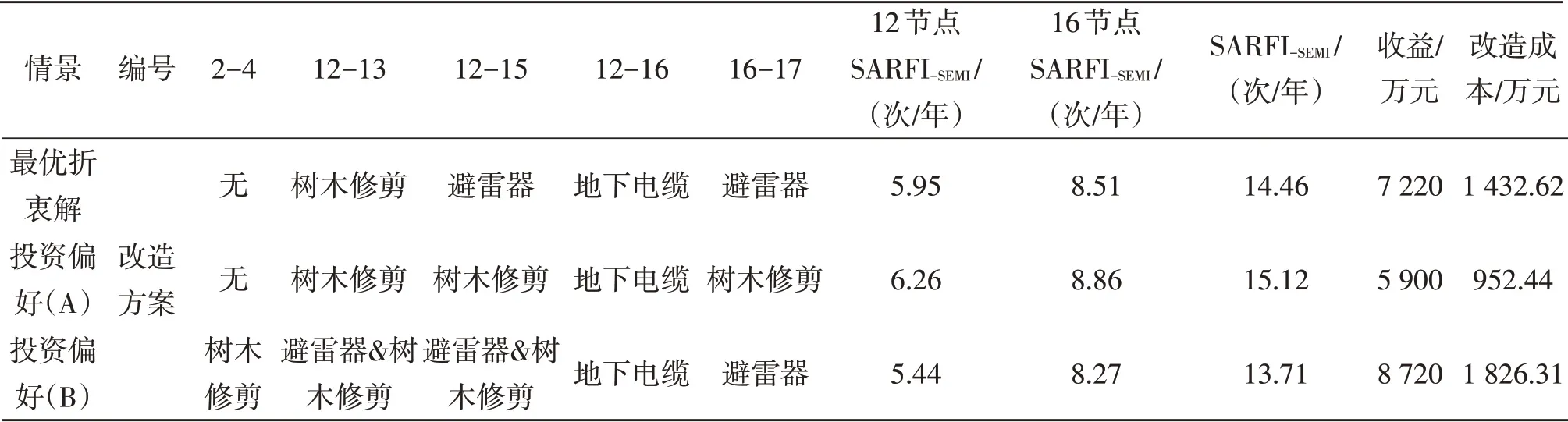
表9 不同偏好下的最优解Table 9 Optimal solutions under different preferences

另外，计算此场景下偏好A 与偏好B 的SARFIsemi及投资成本差值可知，投资成本增加873.93 万元后SARFIsemi指标提升了1.41 次/年。若仅在4.2.1 节仅存在单个敏感节点的场景下，由表7，投资成本增加了941.07 万元后SARFIsemi指标仅提升了0.76 次/年。由此可知，线路改造策略在存在多个敏感负荷接入点的场景下更为有效经济，也反映出线路改造措施更适合作为一种系统级电压 暂降治理手段。

2）以实现用户差异化电压暂降严重程度为目标（场景B）

本文所提多目标优化模型同样可适用于对电压暂降扰动水平具有差异化需求的场景，设敏感节点为12 号节点与16 号节点，可将敏感节点的电压暂降严重程度分别作为优化目标，建立考虑用户差异的线路改造策略多目标优化模型，进行线路改造策略优化，采用SPEA2+SDE 对此三目标优化模型进行求解得到Pareto 最优解集，结果见图6。

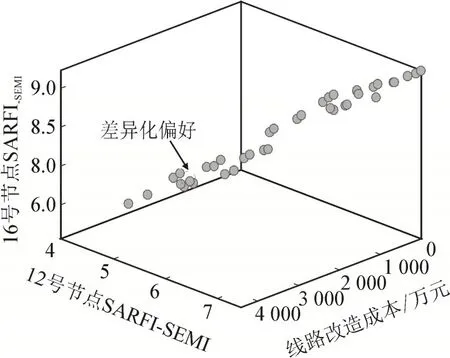
图6 Pareto最优解集（场景B）Fig.6 Pareto solution set（scenario B）

设12 号节点要求SARFIsemi不超过5 次/年，而16 号节点SARFIsemi不超过8 次/年，由Pareto 解集可确定实现该差异化电压暂降水平的线路改造策略见表10，证明所提模型的灵活性，可适用于不同场景的线路改造策略优化，具有较高工程应用价值。

表10 差异化需求下的最优解Table 10 Optimal solution under differentiated demand

5 结语

可实现多个节点电压暂降治理的线路改造策略是一种极具潜力的电压暂降治理技术。为提高基于线路改造策略的电压暂降治理有效性和经济性，本文建立了考虑电压暂降严重程度和投资成本的线路改造策略多目标优化模型，采用SPEA2+SDE多目标进化算法求解。以IEEE 30 节点系统为算例的仿真结果表明，本文提出的线路改造策略多目标优化模型可根据不同决策场景，确定最优考虑电压暂降的线路改造策略，满足决策需求，具备有效性、灵活性和实用性。值得注意的是，电压暂降的治理是供用电双方的共同责任，安装电压暂降补偿设备是用户侧常用的治理手段，将供电侧采取的线路改造与之配合，建立供用电双方电压暂降治理技术协调优化模型是后续值得进一步研究的工作。