计及复合电能质量的配电网附加损耗量化计算与建模仿真
王倍倍,蒋建东
(郑州大学电气工程学院,郑州 450001)
0 引言
电网总损耗的一半以上都是由低压配电网引起的,而低压配电网总损耗中各种电能质量扰动引起的附加损耗占比达15%左右[1-2]。实际运行中的低压配电网存在多种电能质量扰动,研究复合电能质量与低压配电网附加损耗的关系有利于准确量化计算电能质量对低压配电网损耗的影响,提高损耗计算精度,限定各类电能质量扰动指标参数,对配电网节能降损具有指导意义。目前电能质量问题的分析与评估多集中在单一电能质量上,且传统配电网损耗计算未分析电能质量造成的附加损耗,文献[3-5]研究多种三相不平衡度计算方法的区别与适用范围;文献[6]基于动态三相不平衡度进行配电网线损的计算;文献[7]提出计及三相不平衡影响因素的改进等值电阻法;文献[8]分析不同联结方式下的配电变压器在三相不平衡时损耗受到的影响;文献[9]提出计及谐波影响因素的线损计算模型,完成谐波对配电网损耗的量化计算;文献[10]分析电压偏差下配电变压器空载损耗偏差和空载损耗的电压校正。
在分析三相不平衡、电压偏差同时存在时和谐波单独存在时低压配电网附加损耗的基础上,采用谐波三相不平衡度表征指标得到三相不平衡、谐波与电压偏差3 种电能质量问题同时作用时配电网附加损耗的计算模型,并基于Matlab/Simulink软件对复合电能质量下低压配电网附加损耗计算模型的正确性与精确性进行了仿真分析。为方便进一步分析,忽略电压偏差的影响,分析三相不平衡与谐波同时存在时对配电网附加损耗的交互性影响。
1 电能质量扰动下配电网附加损耗
1.1 三相不平衡与电压偏差扰动下附加损耗
1.1.1 配电线路三相不平衡与电压偏差附加损耗
为表征三相不平衡程度,国标用负序不平衡度或零序不平衡度的表示方法不太直观。三相四线制低压配电网中,在零序和负序相位不发生较大变化下,采用IEEE std 112-1991 的方法计算三相电流的不平衡度更合适,并定义为最大三相不平衡度[4]。
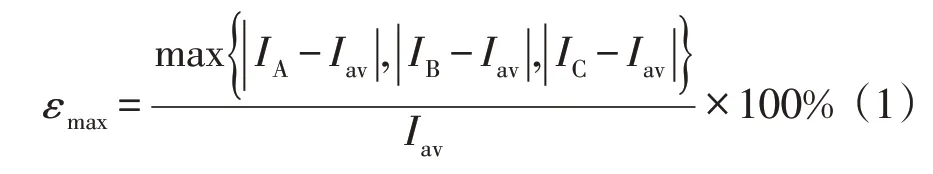
式中:IA、IB、IC为各相电流的有效值,A;Iav为三相电流有效值的平均值,A。
在此引入相不平衡度定义,以便更直观地量化计算相应低压配电网的附加损耗,即用εA、εB和εC表示各相三相不平衡程度如式(2)所示,且εA+εB+εC=0。

式中:Iφ(φ=A,B,C)为各相电流有效值,A。三相四线制低压配电网中,相线附加损耗受电流幅值不平衡影响,而中性线附加损耗受电流幅值与相角不平衡影响。当配电线路中存在电流不平衡与电压偏差时,低压配电网相线的损耗为
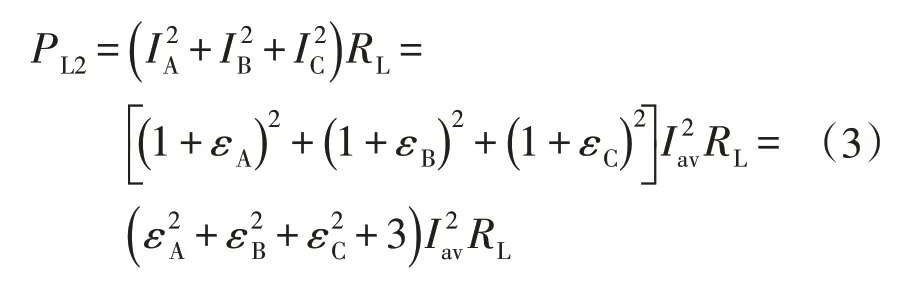
式中:Iav为三相电流不平衡与电压偏差时三相电流有效值的平均值,A;RL为配线基波电阻,Ω。
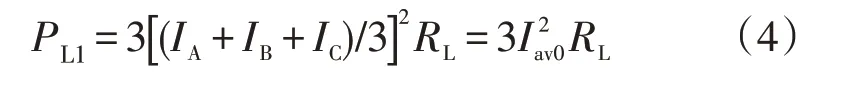
当配电线路中不存在电能质量扰动问题时,低压配电网相线的损耗为式中,Iav0为不存在电能质量扰动问题时三相电流的平均值,A。
三相电流幅值不平衡与电压偏差同时作用下相线上的附加损耗为

同时考虑电流幅值与相角不平衡,三相电流公式为

式中,φA、φB、φB为对应A、B、C 相电流的相角。
中性线电流可表示为
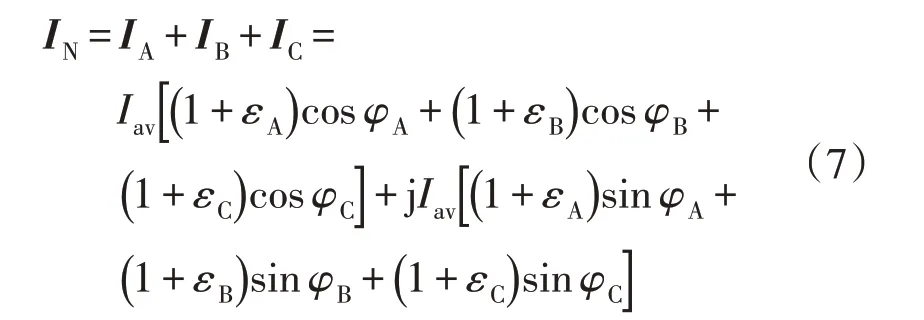
三相电流幅值和相角不平衡时,中性线上的附加损耗为

式中:RN为中性线对应的基波电阻,Ω ;。
三相不平衡与电压偏差因素下低压配电网线路上产生的附加损耗为
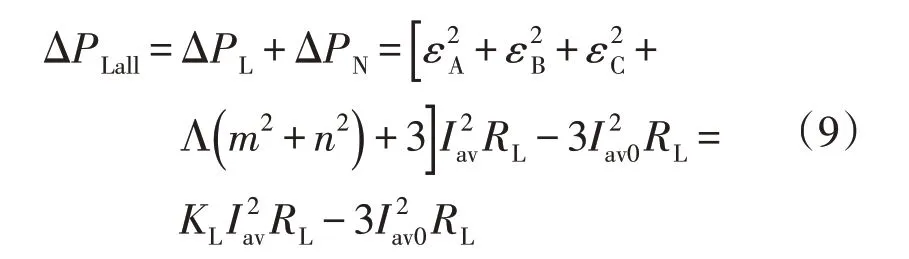
式中:KL为配线的三相不平衡度系数;Λ 为中性线与相线电阻之比,即Λ=RNRL。
1.1.2 配电变压器三相不平衡与电压偏差附加损耗
三相不平衡时变压器的附加损耗分为附加铜耗与附加铁耗。附加铜耗为绕组电阻损耗的增加量,附加铁耗为零序电流在结构件上造成的涡流损耗。
三相不平衡状态下变压器的附加损耗受变压器联结方式的影响[11]。对Dyn11 变压器在电能质量扰动下的附加损耗进行研究,Dyn11 配电变压器正序阻抗、负序阻抗和零序阻抗相等,三相不平衡时二次侧的零序电流造成较小的涡流损耗,可忽略不计。但实际运行中的变压器电压存在偏差时,变压器空载损耗与实际运行电压呈指数关系[12]为
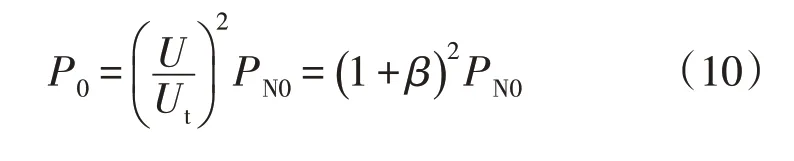
式中:U、Ut分别为变压器的实际运行电压与分接头电压,kV;PN0为变压器的额定空载损耗,W;β为电压偏差百分比即实际运行电压偏离标称电压的程度,%。
当变压器存在三相电流不平衡与电压偏差时,变压器损耗为

式中,RT为变压器绕组归算至低压侧的等效基波电阻值,Ω。
当变压器中不存在任何电能质量扰动时,变压器损耗为
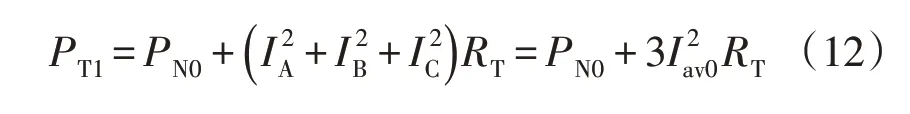
三相不平衡与电压偏差因素作用下低压配电网配电变压器产生的附加损耗为

式中,KT为配电变压器三相不平衡度系数。
三相电流不平衡有幅值不相等和相角不对称,但只有幅值不相等对变压器附加铜耗造成影响,故式(15)即为三相不平衡与电压偏差因素作用下Dyn11 联结方式配电变压器的总附加损耗。
1.2 谐波扰动下附加损耗
1.2.1 配电线路谐波附加损耗
低压配电网架空线路因线路间距大、电压等级低等特点,谐波对线路电阻的影响可忽略不计,即RLh=ΛRNh=RL。
考虑h次谐波影响下架空线路的阻抗为
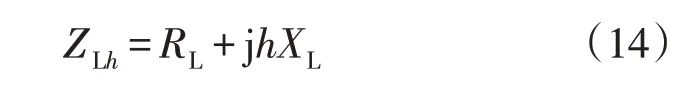
式中,XL为架空线路基波电抗,Ω。
由第h次谐波电流Ih与基波电流I1可得到第h次谐波电流的谐波含有率HRIh=Ih I1×100%,依据谐波电流Ih和谐波电阻Rh可得到低压配电网线路的总谐波附加损耗为
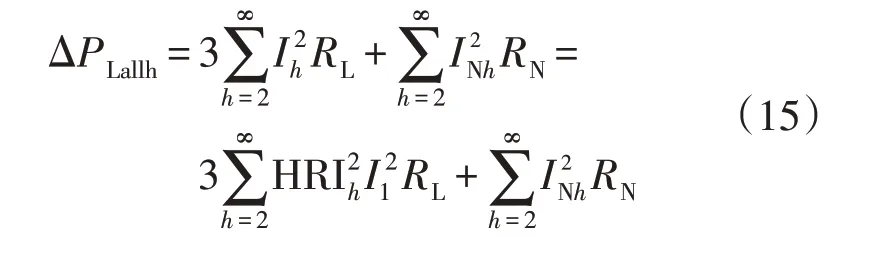
1.2.2 配电变压器谐波附加损耗
当配电变压器存在谐波电流时,谐波对铁耗的影响不大可忽略不计[13]。变压器绕组电阻因谐波产生的趋肤效应与邻近效应而变为谐波电阻。国内外学者提出多种模型计算谐波电阻,文献[14]利用交流电阻系数Fhr定义得到线路谐波阻抗值,但所需参数甚多,计算较为繁琐。IEEE 常采用常规变压器模型,用n倍的直流电阻来替代交流电阻,忽略了变压器绕组电阻受趋肤效应与邻近效应的影响,当存在高次谐波时,误差较大[15]。采用文献[16]提出的通过试验得到变压器内部参数的数值拟合方法,利用叠加定理将一系列独立电源等效为谐波源中各次谐波分量,分别作用到变压器上,由此得到第h次谐波作用下变压器归算至低压侧的谐波电阻与基波电阻之比,公式为

式中:RTh为第h次谐波下归算至低压侧的变压器绕组谐波电阻,Ω。
配电变压器由谐波电流与谐波电阻可得到相应的谐波附加损耗为

1.3 复合电能质量扰动下附加损耗
1.3.1 配电线路复合电能质量附加损耗
低压配电网附加损耗受复合电能质量扰动的影响。为得到三相不平衡、谐波、电压偏差同时作用时配电网附加损耗的计算模型,引入谐波三相不平衡度的定义,如式(18)所示,将三相不平衡度分解为基波与谐波三相不平衡度,从而计算得到基波损耗与谐波损耗。

式中:Iavh为电压偏差下三相电流第h次谐波的平均值,A;εAh、εBh、εCh为A、B、C 各相第h次谐波电流的相不平衡度。
复合电能质量扰动作用下线路的附加损耗为

式中:ΔPLall1、ΔPLallh为配电路线的基波附加损耗和谐波附加损耗,W;KLh为配线第h次谐波电流的三相不平衡度系数;φAh、φBh、φCh为对应各相第h次谐波电流相角;mh=(1 +εAh)cosφAh+(1 +εBh)cosφBh+(1 +εCh)cosφCh;nh=(1 +εAh)sinφAh+ (1 +εBh)sinφBh+。
1.3.2 配电变压器复合电能质量附加损耗
由于三相不平衡与谐波主要影响变压器铜耗与线路损耗,而对变压器铁损影响较小,且三相不平衡度与谐波含有率是基于电压偏差时的三相电流计算出来的,故复合电能质量扰动因素作用下,配电变压器的附加损耗可表示为
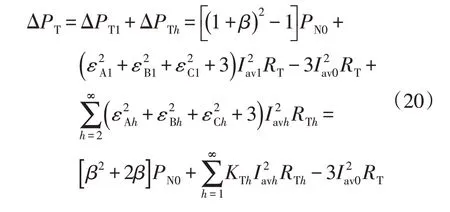
式中:ΔPT1、ΔPTh分别为变压器基波和谐波附加损耗,W;KTh为第h次谐波电流下变压器的三相不平衡度系数。
2 附加损耗模型的仿真分析
为更直观、简便地分析电能质量对低压配电网附加损耗的影响,对低压配电网进行等效简化,见图1。

图1 低压配电网简化图Fig.1 Simplified diagram of low voltage distribution network
在Matlab/Simulink 仿真平台中搭建简单低压配电网,见图2。设定模型中配电线路的相线与中性线参数一致,阻抗为0.239+j0.256 Ω km,长度为0.5 km;负载由3 个单相恒阻抗负载组成,每相额定容量为20 kVA,功率因数为0.9。为在三相不平衡与谐波存在时准确测量功率,搭建了基于幅值与相角的功率测量模块,如图2 中P-Q测量模块所示,模块利用傅里叶模块将每相电压和电流分解为基波、谐波对应的幅值和相角分量,在各相进行基波、谐波功率计算后再叠加即可得到准确的基波与总三相有功、无功功率。
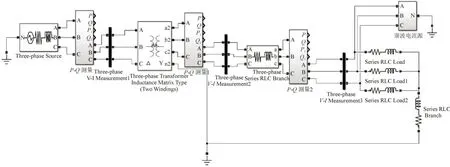
图2 简单低压配电网仿真模型Fig.2 Simulation model of simple low voltage distribution network
2.1 三相不平衡与电压偏差附加损耗仿真分析
总负荷一定条件下,调整谐波电流源无谐波电流注入,通过改变各相负荷分布来改变三相不平衡度,低压配电网首端侧电压从9 kV 等步长变化至11 kV 以改变电压偏差百分比。低压配电网三相不平衡按各相负荷分布的不同可分为3 种情况:情况1(A 相重载B 和C 相轻载)、情况2(A 和B 相重载C 相轻载)、情况3(A 相重载B 相平均负载C 相轻载)。引入损耗增量比的定义来分析电能质量引起的低压配电网附加损耗,如式(21)所示。

式中:P′、P分别为存在电能质量扰动下低压配电网的实际损耗和无任何电能质量扰动下低压配电网的损耗,W。
在总负荷不变且无电压偏差情况下,对3 种情况分别改变各相负荷分布并进行仿真分析,通过功率测量模块能够得到低压配电网附加损耗的仿真数据,从而得到上述3 种情况不同负荷分布下最大电流不平衡度εmax与低压配电网损耗增量比η的关系,见图3。

图3 最大电流不平衡度与配电网损耗增量比的关系曲线Fig.3 Curve of relationship between the maximum current imbalance and loss increment ratio of distribution network
由图3 可知,3 种情况不同负荷分布情况下,低压配电网损耗增量比η都正比于最大电流不平衡度εmax,且增加的比例基本与εmax的平方成正比。在εmax相同条件下时,情况3 在εmax≤52%时损耗增量比曲线明显处于最高位置,εmax≤37.6%时,情况1 和情况2 损耗增量比基本一致,当37.6%<εmax≤52%时,情况1 的损耗增量比曲线逐渐高于情况2,且εmax>52%时,情况1 损耗增量比曲线高于其余两种情况。由此可知,情况3 在εmax≤52%时造成最严重的低压配电网附加损耗,而εmax>52%时,情况1 造成最严重的低压配电网附加损耗。
由图3 分析知在情况3(A 相重载B 相平均负载C 相轻载)不同负荷分布下,最大三相不平衡度εmax低于52% 时引起的附加损耗最严重。为验证三相不平衡与电压偏差存在时计算模型的正确性与精确性,在情况3 与εmax低于52% 条件下,保证无谐波电流注入,改变三相负荷分布以改变最大三相不平衡度,改变低压配电网首端侧电压以得到不同电压偏差百分比。依据理论分析得到的附加损耗计算模型可得到低压配电网附加损耗的计算值,由仿真数据和理论分析的计算数据可得到两者间的相对误差γ见图4。
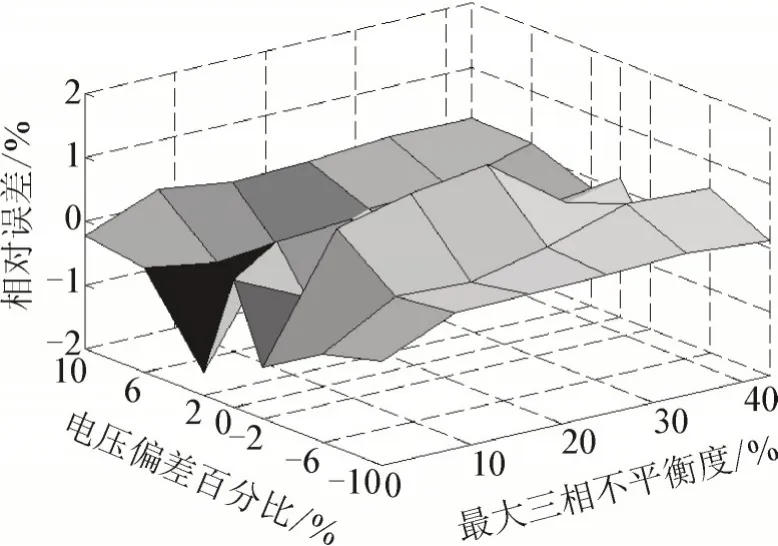
图4 三相不平衡与电压偏差仿真数据与计算数据相对误差Fig.4 Relative error between simulation data and calculation data of three-phase unbalance and voltage deviation
由图4 中相对误差γ可以看出,仿真数据与理论分析计算数据间的相对误差在2% 以内,验证了三相不平衡与电压偏差同时作用下配电网附加损耗计算模型的精确性与正确性。
2.2 谐波附加损耗仿真分析
针对搭建的仿真模型,保证三相负荷分布均匀且配电网首端侧无电压偏差,通过搭建的谐波电流源依次注入5、7、11、13 次谐波,各次谐波电流含有率由各次谐波电流注入的电流幅值改变,7 次和13次正序性与5 次和11 次负序性谐波以注入三相谐波电流的相角来设定,各次谐波不同谐波电流含有率与配电网损耗增量比的关系曲线见图5。

图5 各次谐波含有率与配电网损耗增量比关系曲线Fig.5 Curve of relationship between harmonic contents and distribution network loss increment ratio
分析图5 可知,谐波造成的附加损耗正比于谐波电流含有率,当谐波含量一定时,谐波次数越高,造成的附加损耗越大,但不同次谐波的附加损耗相差不大,原因在于仿真中最高考虑到13 次谐波,变压器绕组电阻受趋肤效应与邻近效应的影响不明显,谐波阻抗变化不大,故引起的附加损耗差别不大。
由理论分析计算模型得到配电网附加损耗的计算数据,由仿真数据与理论分析计算数据计算得到两者间的相对误差γ见图6。

图6 谐波仿真数据与计算数据的相对误差Fig.6 Relative error between simulation data and calculation data of harmonics
由图6 可知,谐波存在时附加损耗的仿真数据与理论分析计算数据的相对误差在2% 以内,验证了谐波扰动作用下配电网附加损耗计算模型的精确性与正确性。
2.3 复合电能质量附加损耗仿真分析
为研究复合电能质量即三相不平衡、谐波与电压偏差同时存在的情况,通过不同的三相负荷分布以调整最大三相电流不平衡度,调整谐波电流源注入的谐波电流幅值以改变谐波电流含有率,调整配网首端电压以改变电压偏差百分比。由分析得到εmax低于52%时三相负荷分布为情况3(A 相重载B相平均负载C 相轻载)引起的附加损耗最严重。在此基础上,改变三相负荷分布可得到A~E 5 种分布状况,由A 到E 对应逐渐增大的最大三相不平衡度。调整谐波电流源注入5 次谐波电流幅值以改变谐波电流含有率,a~f 分别为仅存在谐波扰动时谐波电流含有率为10%~60%对应谐波电流源注入的谐波电流幅值。由此可得到三相不平衡与谐波同时存在时的30 种情况的组合编码见表1。

表1 三相不平衡与谐波组合编码Table 1 Combined coding of three-phase imbalance and harmonics
为验证复合电能质量扰动作用下配电网附加损耗计算模型的正确性与精确性,从9~11 kV 等步长调整配网首端电压,以改变电压偏差百分比,结合表1 中每种情况做仿真分析,可以计算得到计算数据与仿真数据的相对误差γ见图7。

图7 复合电能质量仿真数据与计算数据的相对误差Fig.7 Relative error between simulation data and calculation data of composite power quality
由图7 可知,电压偏差百分比在0~10% 时,仿真数据与计算数据的相对误差在1% 以内,当电压偏差百分比为负值时,仿真数据与计算数据的相对误差基本保证在3% 以内,基本验证了复合电能质量作用下配电网附加损耗计算模型的正确性与精确性。其中几处相对误差较大,主要原因在于当电压偏差百分比为负值时,随着三相不平衡度与谐波电流含有率的增大,附加损耗由负值逐渐增大,当附加损耗值在零点附近时,因基数太小相对误差会出现较大的异常数据。
研究复合电能质量中各单一电能质量对附加损耗的贡献度,为分析方便仅考虑三相不平衡与谐波问题,结合表1 三相不平衡与谐波各种组合情况做仿真分析,得到三相不平衡与谐波不同组合下的损耗增量比变化曲面图见图8。由图8 可知,随着最大三相不平衡度和谐波电流含有率的增大,附加损耗会显著增加,且谐波电流含有率对附加损耗有更大的贡献度。
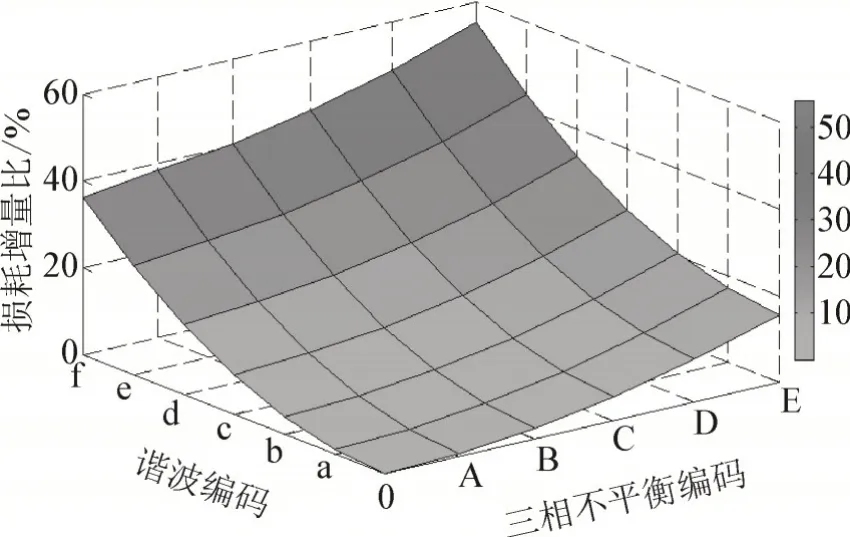
图8 三相不平衡与谐波下配电网损耗增量比变化曲面图Fig.8 Distribution network loss increment ratio variation surface diagram under three-phase imbalance and harmonics
为进一步研究复合电能质量与单一电能质量附加损耗间的关系,将三相不平衡、谐波同时作用下的附加损耗与二者单独作用下的附加损耗进行比较,二者同时作用与单独作用时的附加损耗之差见图9。

图9 复合电能质量与单一电能质量附加损耗差值Fig.9 Difference of additional loss between composite power quality and single power quality equipment
分析图9 可得出以下结论:1)三相不平衡与谐波同时作用下配电网的附加损耗大于二者单独作用的附加损耗之和,即不满足得加定理;2)最大三相不平衡度一定时,二者同时作用与单独作用附加损耗差值随着谐波电流含有率增加而增大;3)谐波电流含有率不变时,二者同时作用与单独作用附加损耗差值随着最大三相不平衡度的增加而增大;4)当谐波电流含有率与最大三相不平衡度较低时,二者同时作用与单独作用附加损耗差值较小,但当谐波电流含有率与最大三相不平衡度较大时,附加损耗差值显著增加。
分析三相不平衡及谐波共同作用的附加损耗不满足叠加定理的原因,由式(19)和式(20)可知,三相不平衡与谐波同时作用下低压配电网的附加损耗可分解为基波不平衡附加损耗与谐波不平衡附加损耗,利用对称分量法分解三相平衡时的谐波电流与三相不平衡时的谐波电流,当h=6k+1(k∈正整数)时,三相平衡时的谐波电流近似等于三相不平衡时的正序电流即Ih≈I1h;当h=6k-1时,三相平衡时的谐波电流近似等于三相不平衡时的负序电流即Ih≈I2h;当h=3k时,三相平衡时中性线的谐波电流近似等于三相不平衡时的零序电流即INh≈IN0h=3I0h。
三相不平衡与谐波同时作用下低压配电网的附加损耗ΔPcomplex可由电流序分量表示为
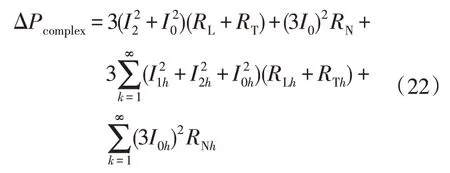
式中:I2、I0分别为三相不平衡时基波电流的负序、零序电流的有效值,A;I1h、I2h、I0h分别为三相不平衡时的谐波电流中第h次谐波电流的正序、负序、零序电流的有效值,A。
三相平衡时谐波作用下低压配电网的附加损耗ΔPhar为
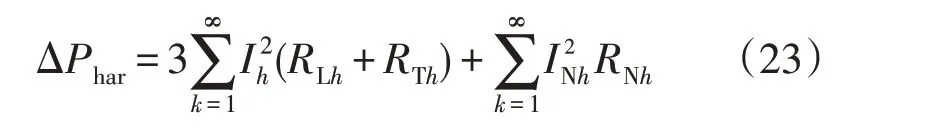
因相同三相不平衡状态下基波电流的各序分量不变,故无谐波且三相不平衡作用下低压配电网的附加损耗ΔPun由基波电流序分量表示为
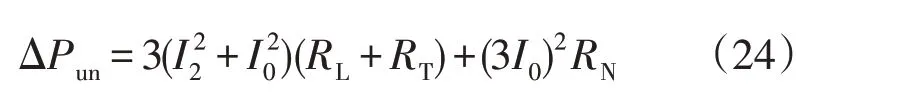
三相不平衡与谐波同时作用下的附加损耗ΔPcomplex与只有三相不平衡作用附加损耗ΔPun之差为三相不平衡与谐波交互影响造成的附加损耗,此部分损耗减去只有谐波作用的附加损耗ΔPhar即为复合电能质量引起的附加损耗与单一电能质量引起的附加损耗差值ΔPd-value即谐波电流因三相不平衡引起的附加损耗,如式(25)所示。

三相不平衡基波电流中含有正序、负序和零序分量,三相不平衡基波电流正序分量近似等于三相平衡时基波正序电流,故三相不平衡基波电流负序与零序分量正是造成三相不平衡附加损耗的原因,且三相不平衡附加损耗值大于零。同理,对于正序性三相不平衡谐波电流,负序与零序分量造成谐波三相不平衡附加损耗;负序性三相不平衡谐波电流,正序与零序分量造成谐波三相不平衡附加损耗;零序性三相不平衡谐波电流,正序与负序分量造成谐波三相不平衡附加损耗。因此,复合电能质量引起的附加损耗与单一电能质量引起的附加损耗差值ΔPd-value大于零,即复合电能质量引起的附加损耗与单一电能质量引起的附加损耗不满足叠加定理,且三相不平衡度与ΔPd-value成正相关特性,三相不平衡度越大越难满足叠加定理。
3 结语
在理论分析三相不平衡、电压偏差同时作用时与谐波单独作用时低压配电网附加损耗计算模型的基础上,由谐波三相不平衡度得到三相不平衡、谐波和电压偏差3 种电能质量同时作用时低压配电网附加损耗的计算模型,仿真分析验证了计算模型的正确性与精确性。为研究复合电能质量中各单一电能质量对附加损耗的贡献度,忽略电压偏差的影响,分析三相不平衡与谐波同时作用时对低压配电网附加损耗的交互性影响,分析得到谐波电流含有率对附加损耗的贡献度更大。仿真发现三相不平衡及谐波同时作用时引起的附加损耗值大于二者单独作用时附加损耗之和,即不满足叠加定理,利用对称分量法分析得出三相不平衡加剧了谐波附加损耗,加剧程度与三相不平衡度成正相关特性,三相不平衡度越大,越难满足叠加定理。

