时变路网下带混合时间窗的车辆路径问题

范厚明，孙秀娜，张跃光，任晓雪，田攀俊

大连海事大学 交通运输工程学院，辽宁 大连 116026

时变路网下带混合时间窗的车辆路径问题（vehicle routing problem with mixed time windows under timedependent network，VRPMTWTDN）是综合考虑多中心联合配送、混合时间窗及车辆行驶速度随时间连续变化的VRP（vehicle routing problem）拓展问题。现实中，物流企业的多个配送中心共同为客户提供配送服务，并根据客户对货物送达时间的不同要求，将客户收货时间约束分为硬时间窗约束和软时间窗约束。如京东推出的“京准达”服务、天猫推出的基于门店的“定时送”服务及哈根达斯的哈根速递等，在客户下单时能预约精准收货时间段，企业须在该时间窗内将货物送到达；未预约精准收货时间段的客户允许配送时间存在一定偏差。同时，路网交通流量的时空差异使得配送车辆的行驶速度不断变化，对货物的送达时间产生一定影响。因此，时变路网下带混合时间窗的多中心车辆路径问题贴近实际配送生产活动，具有重要的理论与应用价值。

VRPMTWTDN 是对多中心车辆路径问题（multidepot vehicle routing problem，MDVRP）、时间依赖型车辆路径问题（time-dependent vehicle routing problem，TDVRP）、带混合时间窗的车辆路径问题（vehicle routing problem with mixed time windows，VRPMTW）的集成问题，已有很多学者对MDVRP、TDVRP 及VRPMTW展开了研究。

针对MDVRP，范厚明等[1]针对多中心联合配送模式下集货需求随机的同时配集货VRP建立两阶段优化模型，并改进变邻域文化基因算法进行求解。Zhang等[2]针对MDVRP，以碳排放量最小为目标建立两阶段优化模型，并设计改进蚁群算法进行求解。Zhen等[3]针对带有时间窗的多行程MDVRP，以配送时长最小为目标建立优化模型，并设计混合粒子群优化算法和混合遗传算法进行求解。Li 等[4]针对MDVRP，以收益最大和配送成本、时间及碳排放量最小为目标建立优化模型，并设计改进蚁群优化算法进行求解。

针对TDVRP，范厚明等[5]考虑客户需求模糊及车辆行驶时间依赖路网速度变化特征，提出时变路网下多车型动态VRP，建立两阶段优化模型，并设计自适应大规模邻域搜索算法进行求解。Ehmke等[6]考虑车辆行驶速度随时间变化及车辆行驶速度等对油耗的影响，以碳排放量最小为目标建立优化模型，并设计禁忌搜索算法进行求解。Alinaghian 等[7]考虑车辆行驶速度的时间依赖性及车辆行驶速度、载重量、道路坡度对车辆油耗的影响，以油耗量最小为目标建立TDVRP优化模型，并设计改进高斯萤火虫算法进行求解。张凯庆等[8]考虑软时间窗约束和车辆速度随时间变化情况，建立以平均客户满意度最大、配送距离及成本最小为目标的优化模型，并设计两阶段算法进行求解。Maha 等[9]考虑车辆行驶速度在路网中不同路段的差异性，建立带时间窗的VRP优化模型，并设计禁忌搜索算法进行求解。付朝晖等[10]针对生鲜电商末端配送问题，考虑生鲜农产品送达客户时的鲜活度及城市路网交通状况的时变性等因素，以总配送成本最小为目标建立TDVRP 优化模型，并设计改进蚁群算法进行求解。

针对VRPMTW，Wang 等[11]针对冷链车辆配送问题，考虑混合时间窗及碳交易政策中的碳价格和交易配额设置对模型求解的影响，以成本最小、碳排放量最小和客户总满意度最大为目标建立优化模型，并设计自适应遗传算法进行求解。Wang 等[12]考虑混合时间窗约束，以配送成本和派遣车辆数最小为目标建立多目标优化模型，并将智能水滴算法与遗传算法相结合进行求解。王勇等[13]针对VRPMTW，将客户重要度与时间窗相结合，建立双层数学模型，并将遗传算法与禁忌搜索算法相结合进行求解。邹宗峰等[14]以运输风险、时间窗惩罚成本、交通状况、道路能力、运输时间最优为目标建立VRPMTW优化模型，并设计多目标遗传算法进行求解。

通过梳理以上相关文献可见，目前还没有针对VRPMTWTDN 的研究成果，且MDVRP、TDVRP 及VRPMTW的研究还存在以下不足：（1）现有针对TDVRP的研究多以阶梯分段函数表示全天道路车辆速度变化情况，未考虑车辆行驶速度的连续变化。（2）现有考虑车辆行驶速度连续变化的研究多假设车辆单位距离的油耗是固定的，鲜有考虑车速、载重量等对油耗的影响。（3）现有关于带时间窗的车辆路径问题的文献，多数单独考虑软时间窗或硬时间窗，较少研究VRPMTW。针对以上不足，本文综合考虑多中心联合配送，不同客户对服务时间的需求差异，车辆行驶速度随时间连续变化以及车速、载重量对油耗的影响，对VRPMTWTDN展开研究。

1 问题分析

1.1 问题描述

由配送区域路网构成完备的有向图G=(V,E)中，节点集合为V=V0⋃V1⋃V2，其中V0={1,2,…,m} 为配送中心集合，V1为未预约精准收货时间段的客户集合，V2为预约精准收货时间段的客户集合；E={(i,j)|i,j∈V,i≠j}为边集合，各配送中心间无路径连接，lij为i、j两节点之间的距离，tij为车辆在i、j两节点之间的行驶时间；K为所有配送中心的车辆集合，车型相同，最大载重量为Q,Ki(i∈V0)为各配送中心i(i∈V0)的车辆集合，k为配送车辆集合K中任意一辆车，Sk为车辆k服务的客户集合，Fijk为车辆k在i、j两节点之间的燃油消耗量，燃油价格为c1，单位车辆的派遣成本为c2；车辆行驶速度v={v1,v2,…,vl}是连续变化的；车辆k从配送中心i出发的时刻为Tik，到达节点i的时刻为，对客户i的开始服务时刻为，车辆完成所有配送任务后在各配送中心车辆数守恒原则下就近返回任一配送中心；客户i的需求量为di，单位货物装卸时间为δ,配送中心有统一的工作时间窗[Ts,Tf],[ETi,LTi]为预约精准收货时间段客户i(i∈V2)的时间窗，车辆须在该时间窗内为客户i提供服务[ETi,LTi]为未预约精准收货时间段客户i(i∈V1)的期望服务时间窗，[EETi,ELTi](EETi≤ETi≤LTi≤ELTi)为其最大容忍时间窗，车辆须在[EETi,ELTi]内为客户i提供服务，在[EETi,ETi] 到达的单位惩罚成本为c3,在[LTi,ELTi] 到达的单位惩罚成本为；决策变量xijk表示车辆k是否从点i到达点j，是为1，否为0。

图1为研究问题的示意图，配送区域有2 个配送中心、25个客户，每个配送中心拥有若干车辆。根据现有客户位置及时间窗进行优化得到图1所示的5条配送路径，其中车辆1、车辆3 和车辆5 均返回原配送中心，车辆2和车辆4返回就近的配送中心。

图1 研究问题的示意图Fig.1 Schematic diagram of research problem

1.2 速度时间依赖函数的确定

现有对TDVRP 的研究，多以阶梯分段函数表示路段的车辆行驶速度，在某一时间节点速度突变，不能很好地刻画高峰时段配送区域路网对车辆行驶速度的限制，不符合现实中车辆行驶速度连续变化的特点。鉴于此，本文参考文献[15]，以多项式函数表示车辆行驶速度随时间的连续变化，如图2所示。

图2 车辆速度时间依赖函数Fig.2 Vehicle speed-time dependence function

1.3 车辆油耗计算

车辆油耗量取决于车辆行驶时间、行驶速度、车型和道路状况等因素，本文借鉴文献[16]研究结果，考虑车速、载重量对油耗的影响，建立油耗计算模型。

行驶时间dt内的燃油消耗量dfij为：

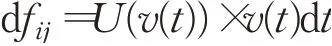
式中，U(v(t))是空载车辆的燃油消耗率，单位是L/km。

U(v(t))与空载车速之间的关系为：

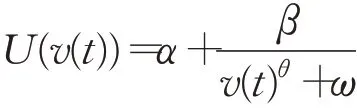
式中，α、β、θ和ω由道路和车辆状况决定。

空载车辆k在路段(i,j)上的燃油消耗量fijk为：

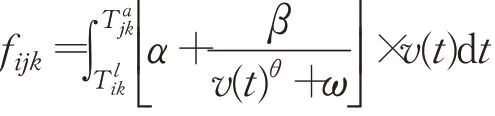
式中，Tl ik为车辆k离开i点时刻，Ta jk为车辆k到达j点时刻。

假设油耗增量与车辆载重增量呈线性关系[21]，载重每增加L，油耗增加s（百分比），则载重量为Qik的车辆k在路段(i,j)上的油耗Fijk为：

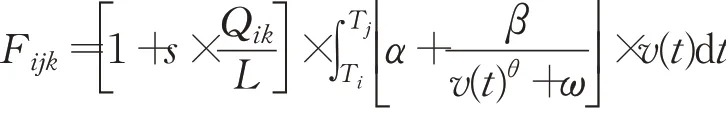
2 模型建立

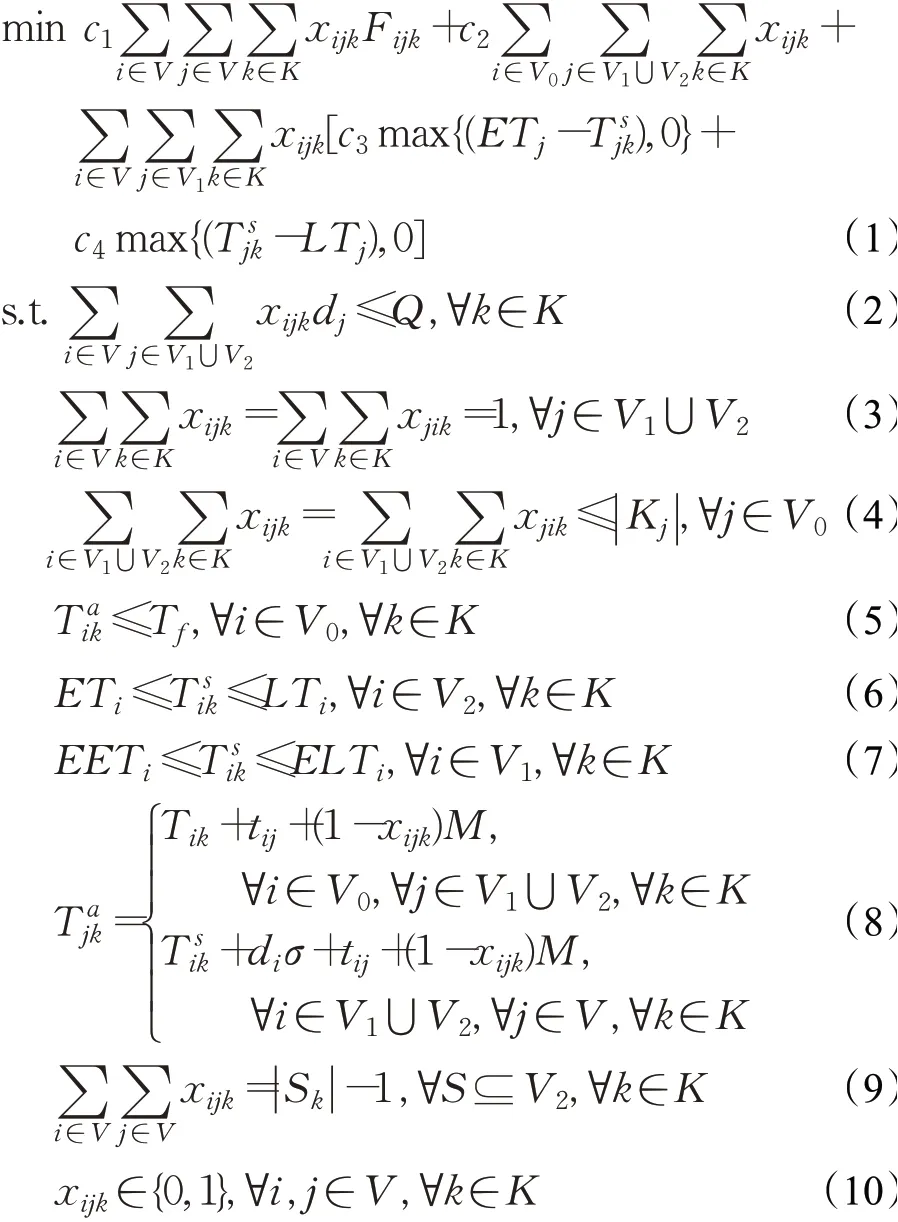
式（1）为目标函数式，第一部分为油耗成本，第二部分为车辆派遣成本，第三部分为时间窗惩罚成本；式（2）表示车辆的载重限制；式（3）表示各客户点车辆进出平衡，且客户只能被服务一次；式（4）表示各配送中心出发和返回的车辆数一致，且不超过其最大车辆数；式（5）表示各车辆须在配送中心工作截止时间前返回配送中心；式（6）和式（7）为车辆对客户i开始服务时刻的约束；式（8）为车辆从节点i出发到达节点j时刻的计算方法，其中M为无穷大值；式（9）为消除子回路约束；式（10）为决策变量属性。

3 算法设计

本文所提问题考虑多中心联合配送、混合时间窗及车辆行驶速度连续变化等因素对配送方案制定的影响，属于NP-hard问题，求解过程复杂，用精确算法求解较为困难，因此考虑采用启发式方法进行求解。遗传算法（genetic algorithm，GA）具有快速随机的全局搜索能力，可同时对搜索空间中的多个可行解进行评估，但搜索具有盲目性，在求解到一定范围时常做大量无为冗余迭代，使求解效率低；大规模邻域搜索算法既能保持大规模邻域的寻优能力，又能克服低效的弱点，从而提高算法的求解能力。本文根据VRPMTWTDN 模型特点，将传统遗传算法与大规模邻域搜索算法相结合，设计自适应遗传-大邻域搜索算法（adaptive genetic algorithm with large neighborhood search，AGA-LNS）进行求解。

自适应遗传-大邻域搜索算法相比于传统遗传算法，通过大规模邻域搜索提高寻优能力，改进的交叉变异算子对可行解不断进行优化，且以最优个体持续未改变代数作为迭代停止的判断依据，避免做大量无为冗余迭代，提高求解效率；相比于传统邻域搜索，既能保持大规模邻域的寻优能力，又能克服低效的弱点，局部最优解的质量更好，但迭代耗时较长。自适应遗传-大邻域搜索算法早期寻优主要依靠遗传算法的全局搜索能力和大邻域算法的局部搜索能力，通过改进的交叉操作和变异操作可以快速接近全局最优解；后期寻优主要依靠大邻域搜索算法的局部搜索能力，通过移除-插入操作对当前最优解进行摧毁和重建，有利于算法跳出局部最优解，弥补了遗传算法后期收敛速度慢，容易造成冗余迭代的缺点。遗传算法与大邻域搜索算法相结合可以有效平衡算法的局部寻优能力和全局寻优能力，具有较强的求解性能。

自适应遗传-大邻域搜索算法流程如图3所示。

图3 AGA-LNS流程图Fig.3 Flow chart of AGA-LNS

3.1 初始解的构造

初始解的质量很大程度上影响着算法的求解质量和求解效率，若随机生成初始种群，极易产生大量无效个体，增加收敛代数。为提高可行解的生成概率，采用整数编码方式，设计“先客户后中心”的两阶段方法生成初始解。首先进行客户点分组并确定服务顺序，然后确定发车时间和返回的配送中心及到达各节点的具体时刻。此方式可保证生成的初始种群均为可行解，且具有一定随机性，增加了初始种群的多样性和有效性，避免过早陷入局部最优。具体步骤如下：

阶段1 客户点分组并确定服务顺序。

步骤1 随机派遣一辆车，用虚拟配送中心0表示其出发的配送中心，根据客户允许的最早开始服务时刻由早到晚对所有未服务的客户进行排序，并从前n个客户中随机选取一个作为新派车辆服务的第一个客户并将其插入到当前路径。

步骤2 求出从当前客户出发到所有未服务客户的到达时刻并判断其是否在该客户时间窗内，从到达时刻在客户时间窗内的所有客户集合中选择开始服务时刻最小的客户插入到路径，若所有客户的到达时刻都早于其时间窗开始时刻，则选择到达时刻距其时间窗开始时刻最近的客户插入到当前路径。重复以上操作，直至车载量、未服务客户的时间窗或返回配送中心时刻中任一约束不满足，则新派一辆车。

步骤3 重复步骤1 和步骤2，直至所有客户的配送任务安排完毕。

阶段2 确定车辆出发和返回的配送中心及到达各节点的具体时刻。

步骤4 替换车辆出发和返回的虚拟配送中心0：计算每条路径首尾客户距离各配送中心的距离，依次选择与各路径首个客户距离最小的配送中心替换车辆出发的虚拟配送中心0，若所选配送中心无可派遣车辆，则选择距离次近的配送中心，直至替换完毕；然后依次选择与各路径末尾客户距离最小的配送中心替换车辆返回的虚拟配送中心0，若所选配送中心不满足车辆守恒，则选择距离次近的配送中心，直至替换完毕。以各车辆服务的首个客户的时间窗开始时刻作为其到达该客户点的时刻，计算车辆从配送中心的出发时刻、到各客户点的服务时刻及返回配送中心的时刻。

图4 为染色体编解码过程示意图，以10 个客户（编号为1～10）和2个配送中心（编号为11～12）为例，按照上述步骤生成初始解。首先在染色体起始位置插入车辆起始虚拟配送中心0，再将所有客户按最早开始服务时刻由早到晚排序，从前5 个客户中随机选取客户3 作为车辆服务的首个客户，再计算从客户3到所有未服务客户的到达时刻，选出最佳后续客户1 插入到路径中，按照相同方法选出后续客户2、5，直至不满足任一约束时，车辆返回虚拟配送中心0。以此类推，划分后的路径如图4（a）所示，再根据步骤4 所述操作先后确定车辆出发、返回的配送中心替换虚拟配送中心0，得到初始解如图4（c）所示。

图4 染色体解码示意图Fig.4 Chromosome decoding diagram

3.2 进化操作

进化操作首先进行基于时差插入法的自适应交叉变异，然后通过成对的移除、插入算子将路径中的客户按照一定规则移除，再将被移除的客户按照一定规则插入到路径。由于每一次交叉、变异操作或插入-移除操作都可能减少染色体中的车辆数，每次进化操作后按照3.1节中步骤4描述的方法重新确定车辆出发和返回的配送中心。

3.2.1 时差插入法

客户m插入到客户i和客户j之间的时间约束条件为：车辆在客户m的开始服务时刻不晚于客户m容忍的最晚接受时刻Tm；插入客户m后，车辆到达客户j的时刻不晚于客户j的最晚开始时刻。插入的时间约束如下：

式中，车辆在客户m的最早完成时刻EFm和最晚开始时刻LSm计算方法如式（12）、（13）所示，其中客户i为客户m的前序客户，客户j为客户m的后序客户。

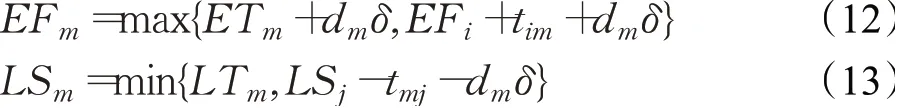
时差插入法的具体步骤如下：

步骤1 计算所有客户的最早完成时刻和最晚开始时刻。

步骤2 按照时间约束确定客户m可插入的位置，并计算假设插入客户m后各位置的目标增量。

步骤3 选择目标增量最小的位置插入客户m，若所有位置均不满足插入条件，则新派遣一辆车。

步骤4 更新所有客户的最早完成时刻和最晚开始时刻。

步骤5 重复上述操作，直至所有待插入客户全部插入路径中。

3.2.2 交叉算子和变异算子

交叉变异概率值的设定对解的寻优过程有很大影响，传统遗传算法的交叉概率和变异概率根据经验和主观判断设置为定值，若设置较小，则会使个体进化速度较慢，增加算法的求解时间，若设置较大，则容易在算法求解后期破坏优秀个体，使算法陷入局部最优解。为提升算法的性能，参考文献[17]设置自适应交叉变异概率，相比于常规交叉变异概率，自适应交叉、变异可以根据每次迭代所得新个体的适应度值适应性地调整交叉、变异概率，在进化前期以较大的交叉变异概率加速个体进化，增加解的多样性，避免过早陷入局部最优，在进化后期交叉变异概率逐渐减小，避免破坏优秀个体。自适应交叉、变异概率计算方法如式（14）、（15）所示。

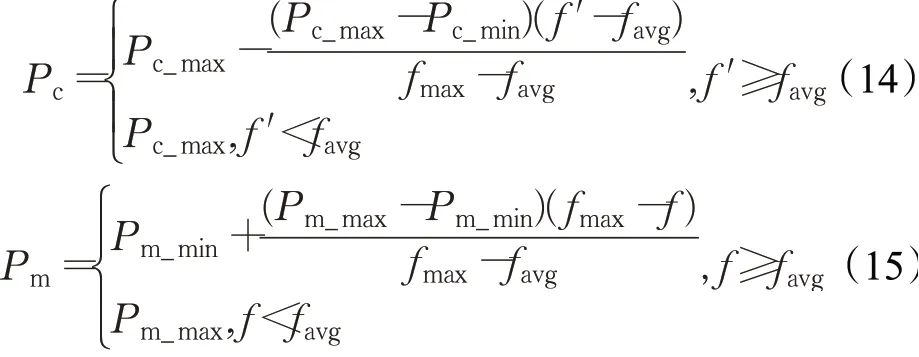
式中，Pc_max、Pm_max分别是交叉概率区间和变异概率区间的最大值，Pc_min、Pm_min分别是交叉概率区间和变异概率区间的最小值，f为个体适应度值，其大小为目标函数值的倒数，f′为进行交叉父本中最优个体的适应度值，fmax为所有个体适应度值中的最大值，favg为所有个体的平均适应度值。

考虑车辆的服务时刻不能违反硬时间窗客户的时间要求，若按传统交叉变异进行操作，则会破坏原有可行解，产生大量不可行解，对此，在交叉算子和变异算子中引入时差插入法，以客户的时间窗约束作为种群优化的前提条件，保证每次迭代后均生成可行解，提高可行解的生成率，进而提高求解质量。其中交叉操作对两个父代个体进行部分交换后保留较优解，提高种群多样性，变异操作可减少个体中子路径的数量，即减少配送方案中派遣的车辆数，有利于提高求解质量，降低配送成本。

（1）交叉操作：在两个父代染色体中分别随机选取一条子路径并进行交换，再对交换后的染色体进行修复。首先删除因交换导致重复的客户，然后在满足车辆载重等约束的基础上，通过时差插入法插入因交换路径导致染色体中缺失的客户。以图5为例，将父代染色体a中子路径11—1—7—4—10—11与b中子路径11—9—8—10—12 进行交换得到a1 和b1，删除a1 中重复客户8、9及b1中重复客户1、7、4得到a2和b2，再通过时差插入法将a2 中缺失的客户1、7、4 插入a2 中、将b2 中缺失的客户8、9插入b2中得到a3、b3。

（2）变异操作：在父代染色体中随机删除客户数最少的子路径，然后在满足所有约束的前提下采用时差插入法重新插入删除的客户。以图6 为例，删除染色体a中包含客户数最少的一条子路径13—6—8—12得到a1，再采用时差插入法将客户节点6、8重新插入得到a2。

3.2.3 移除算子和插入算子

每次迭代时，在交叉变异后引入基于时差插入法的移除算子和插入算子进行种群优化。先通过移除算子删除当前解中的μ 个客户，再通过插入算子将删除的客户重新插入构造新解。在每次迭代中多次使用移除-插入组合算子对可行解进行摧毁和重建，可以增加解的多样性，扩大搜索范围，提高算法的全局寻优能力。移除算子和插入算子如下：

（1）移除算子

①随机移除算子：随机移除当前解中的μ 个客户。

②最远距离移除算子：计算当前解中所有客户的距离成本，移除距离成本D(m) 最大的客户m ，其中m 的前序客户，j 为m 的后序客户。具体操作如图7所示，图中D1、D2 代表配送中心，其余为客户点，箭头上的数值为节点间的距离。

③最远偏离客户中心移除算子：移除每辆车服务的客户集合中与其他所有客户的中心点距离最远的客户，即移除客户位置偏差D(j)最大的客户。客户j 的位置偏差为为客户j的位置坐标，(X,Y)为一辆车服务的除客户j 外其他所有客户的中心点坐标。

（2）插入算子

①贪婪插入算子：在满足所有约束的基础上采用时差插入法找出客户m 的可插入位置，计算插入距离成本C(m)，并将客户m 插入C(m)最小的位置，其中C(m)=dim+dmj-dij,i 为插入位置的前序客户，j 为插入位置的后序客户。

②最好时间插入算子：在满足所有约束的基础上采用时差插入法找出客户m 的可插入位置，并计算其时间偏差量BT(m)，并将客户m 插入BT(m)最小的位置，其中

3.2.4 迭代终止条件

当最优个体持续未改变的代数达到最优个体持续未改变的最大代数MAXGEN 时停止迭代，输出结果。

4 算法验证与算例分析

4.1 算子的选择

移除和插入算子是成对出现的，为确定不同算子求解的有效性，采用Cordeau 标准算例库中MDVRPTW（multi-depot vehicle routing problem with time windows）标准算例对交叉、变异算子和6组移除-插入算子进行测试，各算子求解各算例所得结果的平均值如表1 所示。其中Ai(i=1,2,3)表示三种移除算子，Bi(i=1,2)表示两种插入算子，BKS为标准算例库中已知最优解，Avg为各算子求解所有算例所得结果的平均值，GAP为Avg与BKS的误差。由表1 可知，交叉算子的求解性能最好，平均误差为4.1%，其次为变异算子，平均误差为4.6%，移除-插入算子组合中，随机移除算子和贪婪插入算子组合求解性能最好，平均误差为12.3%，其次是最远距离移除算子和贪婪插入算子的组合，平均误差为32.1%。为保证求解质量及求解速度，选取以上两种移除-插入算子组合应用于算法中进行可行解的摧毁和重建。

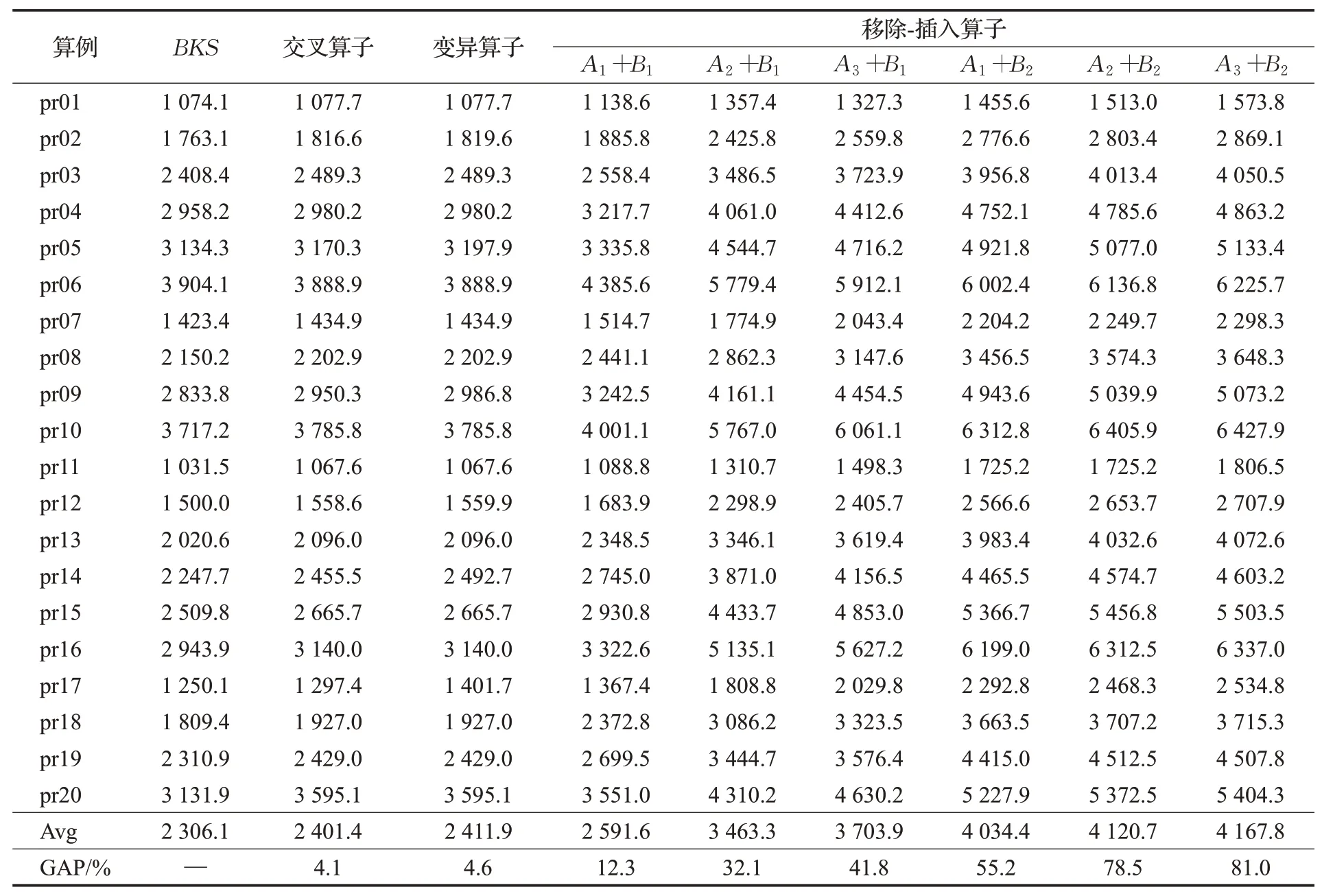
表1 算子测试结果Table 1 Test results of operators

4.2 算法验证

4.2.1 算法测试

目前没有VRPMTWTDN 的标准算例库，选择MDVRPTW测试AGA-LNS的性能。采用MATLAB R2018b进行算法编程，操作系统为Windows10，电脑内存为8 GB，CPU 为Intel i7-7700M，主频3.60 GHz。设置种群规模NIND为100，MAXGEN为30～50。

选择Cordeau 标准算例库中MDVRPTW 的20 个算例测试AGA-LNS，表2给出了禁忌搜索算法（tabu search，TS）[18]、变邻域搜索算法（variable neighborhood search，VNS）[19]、基于复合邻域的离散萤火虫算法（discrete firefly algorithm with compound neighborhoods，DFACN）[20]、混合遗传算法（hybrid genetic algorithm，HGA）[21]及AGA-LNS 的求解结果。其中N为客户规模，M为配送中心数，K为配送中心最大车辆数，Q为车辆最大载量，BKS为标准算例库中已知最优解，C为算法求解的最优值，GAP为算法求得结果与BKS的相对误差，t为算法运行10 次的平均耗时。由表2 可知，在求解质量方面，AGA-LNS 求得的最优值与BKS的最小误差为-3.36%，最大误差为4.39%，当客户规模增大时，相对误差有所增大。AGA-LNS的求解结果优于TS和VNS，略差于DFACN和HGA，求解耗时小于HGA。通过对比分析运算结果，可验证AGA-LNS的有效性。

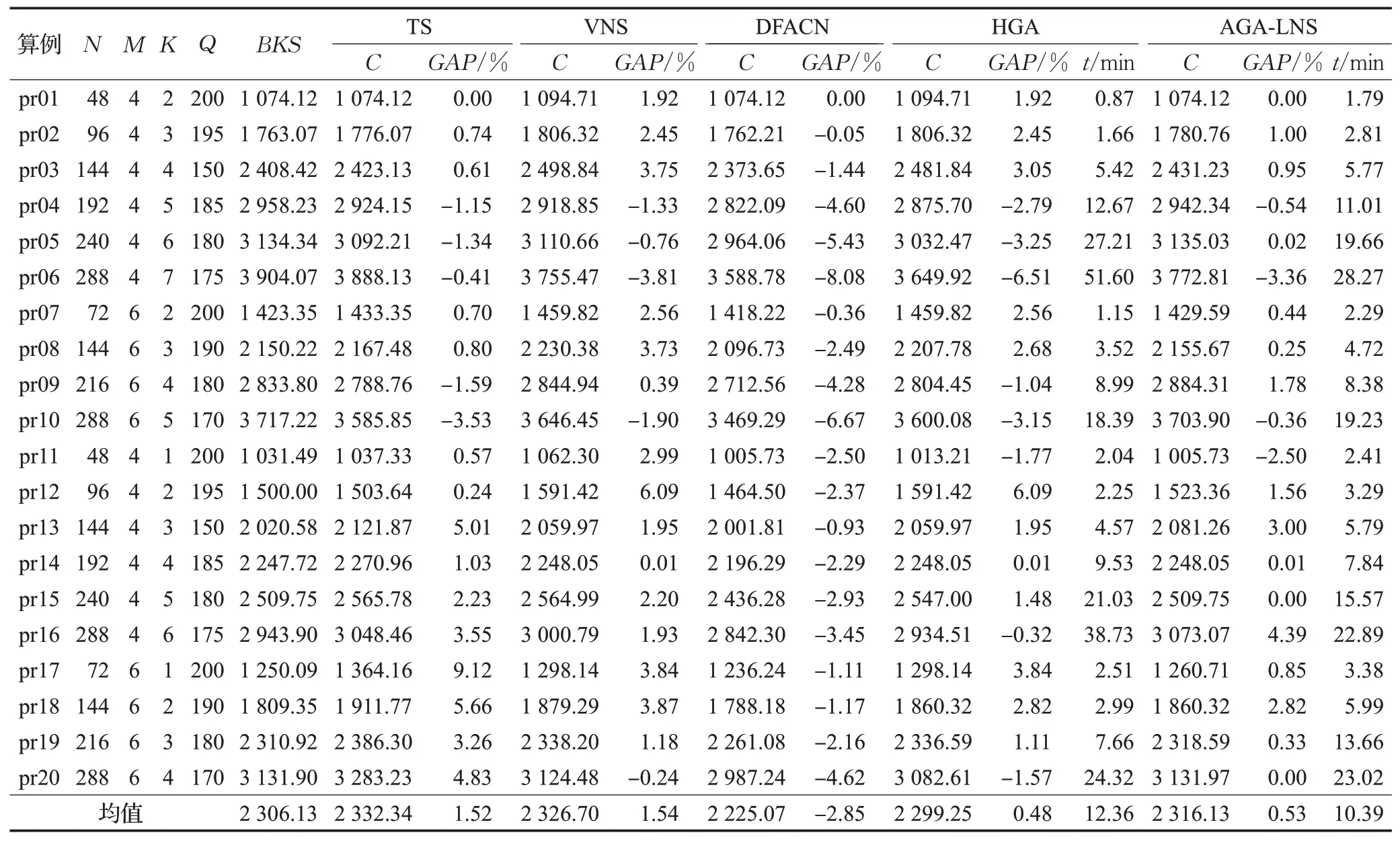
表2 算法测试结果Table 2 Algorithm test results

4.2.2 交叉变异概率分析

为验证自适应交叉变异概率相比于常规交叉变异概率的优越性，设置三种交叉概率0.40、0.65、0.90，三种变异概率0.02、0.11、0.20，采用Cordeau标准算例库中前10 个MDVRPTW 标准算例对九种概率组合进行测试，并与本文自适应交叉变异概率下算例的求解结果进行对比，如表3所示。其中C为运用自适应交叉变异概率求得的最优解，Avg为所有算例最优解的平均值，GAP为Avg与C平均值的相对误差。由表3 可知，九种交叉变异概率组合中，交叉、变异概率分别为0.65、0.20时求解结果最优，但与自适应交叉变异概率下的求解结果相比仍相差1.20%，可见运用自适应交叉变异概率进行求解相比于常规交叉变异概率更有优越性。

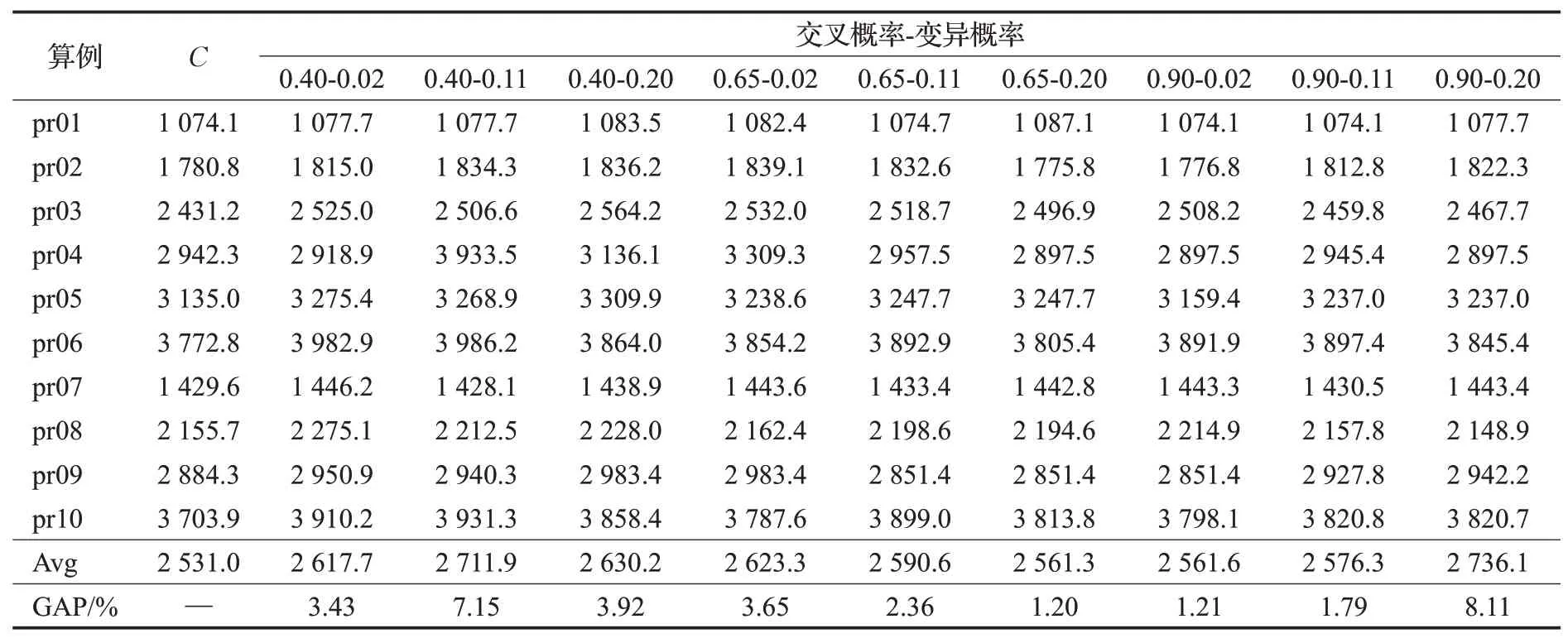
表3 不同交叉变异概率下算例求解结果Table 3 Example results under different crossover and mutation probability

4.3 算例分析

VRPMTWTDN问题复杂，没有通用的算例集，设计两个算例并用AGA-LNS求解其配送方案。

4.3.1 算例1

假设在配送路网中有4 个配送中心和48 个客户，配送中心坐标分别为（4.163，13.559）、（21.387，17.105）、（-36.118，49.097）、（-31.201，0.235），随机生成48 个客户坐标并将其作为客户节点，其中横坐标与纵坐标分别在[-75，50]和[-30，100]范围内随机生成，客户需求量在[0.015，0.375]内随机生成，客户时间窗在[05：00，17：00]内随机生成。每个配送中心的工作时间窗均为[05：00，17：00]，最大车辆数均为4，车辆载重量为3 t，单位车辆的派遣成本为500元，油耗成本c1=5.5 元/升，早到单位惩罚成本c3=30 元/h，晚到单位惩罚成本c4=60 元/h，每吨货物装卸时间为0.5 h，交叉概率Pc、变异概率Pm的取值区间分别为[0.4，0.9]、[0.02，0.2]。根据文献[20]相关研究，参数α、β、θ和ω设为30、100、1 和-5。配送中心根据各车辆第一个待服务客户的时间窗合理安排出发时间，确保其在首个待服务客户的时间窗内到达。用AGA-LNS求解得到如表4所示的配送方案，其中YC代表油耗成本，TC代表时间窗惩罚成本，ZC代表配送方案总成本。

表4 算例1配送方案Table 4 Distribution scheme of Example 1

4.3.2 算例2

假设在配送路网中有4个配送中心和96个客户，配送中心坐标分别为（6.229，10.590）、（32.663，44.730）、（48.807，49.792）、（33.179，-4.968），随机生成96 个客户坐标并将其作为客户节点，其中横、纵坐标分别在[-40，87]和[-42，80]范围内随机生成，客户需求量在[0.015，0.375]内随机生成，客户时间窗在[05：00，17：00]内随机生成，其他参数设置与算例1相同，用AGA-LNS求解得到如表5所示的配送方案。

表5 算例2配送方案Table 5 Distribution scheme of Example 2

4.3.3 实验结果分析

选用不同客户规模的算例（4.3.1、4.3.2 小节中的算例及MDVRPTW 标准算例pr03、pr04）对AGA-LNS 进行算法分析及敏感性分析，未给出的其他参数与算例1设置相同。

（1）算法分析

为验证AGA-LNS 的有效性，采用自适应遗传算法（AGA）、大邻域搜索算法（LNS）求解不同客户规模算例的配送方案，并与AGA-LNS 的求解结果进行对比分析。其中AGA 采用本文设计的交叉变异操作，LNS 选用随机移除算子和贪婪插入算子组合、最远距离移除算子和贪婪插入算子组合。表6 给出了3 种算法运行10次的结果，其中C为10次运算结果中的最优解，t为算法平均耗时，GAP1 为AGA-LNS 与AGA、LNS 所求结果的误差，GAP2 为AGA-LNS 与AGA、LNS 求解耗时的误差。由表6 可知，AGA-LNS 与AGA、LNS 相比，在求解时长和求解质量上都有显著优势，因此AGA-LNS能较好地解决VRPMTWTDN；对比AGA 和AGA-LNS的求解结果可知，客户规模相同时，AGA-LNS的求解结果相对于AGA 的求解结果均有所改善，平均改善了2.73%，可见在自适应遗传算法的交叉变异操作后加入大邻域搜索可改善自适应遗传算法陷入局部最优解的问题，提高求解质量。

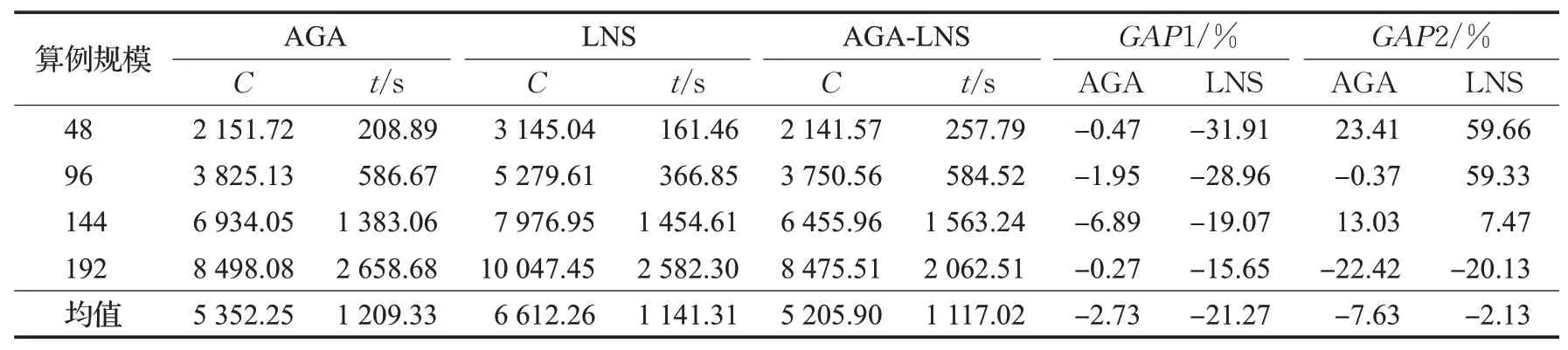
表6 不同算法求解结果对比Table 6 Comparison of solution results of different algorithms

（2）敏感性分析

①混合时间窗比例的影响

为验证软硬时间窗客户数量的比例变化对配送方案制定的影响，本文针对不同客户规模，分别设置了6种软硬时间窗客户数量比例（软时间窗客户数∶硬时间窗客户数=S∶H）。表7给出了算法运行10次的结果，其中N为客户规模，C为10次运算结果中的最优解，GAP为不同软硬时间窗客户数量比例下10次运算结果的最优解与S∶H=1∶1 时求得最优解的相对误差。由表7 可知，相同客户规模下，最优解随着硬时间窗客户数量比例的增大而增大，即软时间窗和硬时间窗客户总数一定，硬时间窗客户越多，其最优配送方案总成本越高。

表7 软硬时间窗客户不同比例下最优配送方案总成本Table 7 Total cost of optimal distribution scheme under different ratios of customers with hard and soft time windows

②车辆行驶速度的影响

为验证车辆行驶速度对配送方案制定的影响，本文对不同客户规模算例在车辆匀速行驶情况下进行求解。表8给出了算法运行10次运算结果，其中N为客户规模，Case1 代表速度连续变化，Case2 代表速度恒为40 km/h，Case3代表速度恒为50 km/h，Case4代表速度恒为60 km/h，C为10次运算结果中的最优解，GAP为车辆匀速行驶时10次运算结果中的最优解与车速时间依赖时求得最优解的相对误差。由表8可知，相同客户规模下，不同行驶速度下求得的最优解与速度时间依赖时求得的最优解具有一定误差，如客户规模为48时，误差分别为1.05%、-0.79%、-1.68%。其中车辆行驶速度为50 km/h时的求解结果与本文设置的速度时间依赖函数下求解结果的误差最小，车辆行驶速度增大或减小，与本文设置的速度时间依赖函数下求解结果的误差均增大。综合分析，在制定配送方案时考虑车辆行驶速度时间依赖性具有重要意义。

表8 不同车速下最优配送方案总成本Table 8 Total cost of optimal distribution scheme under different vehicle speeds

表9给出了速度连续变化时与恒定速度时各自运行10 次的平均求解耗时。其中Case1 代表速度连续变化，Case2代表速度恒为50 km/h，GAP为速度连续变化时算例求解的平均耗时与恒定速度时算例求解的平均耗时的相对误差。由表9可知，速度连续变化时算例求解平均耗时比速度恒定时算例求解平均耗时平均多63.82%，因此考虑车辆速度连续变化增加了算法实现的时间成本约63.82%，但配送中心通常在配送前一天根据已有订单制定配送方案，因此速度时间依赖下的算法时间成本是可行的。

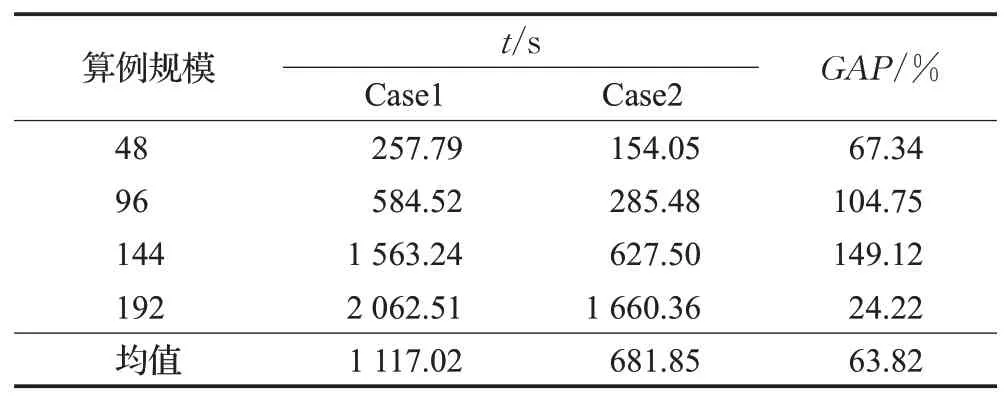
表9 不同车速下算例求解耗时Table 9 Example solving time under different vehicle speeds

5 结束语

本文考虑配送路网中车辆速度的连续变化，并按照客户对配送时间的不同要求对其服务时间窗进行分类，对VRPMTWTDN 进行研究，建立了以配送成本最小化为目标的优化模型，并设计了自适应遗传-大邻域搜索算法求解配送方案，并实验验证了其有效性，结论如下：

（1）模型中不仅考虑了配送中心间配送资源的共享及混合时间窗，还考虑了车辆速度连续变化及车速、载重量对油耗的影响，虽增加了问题求解难度，但更贴近配送生产活动的实际。

（2）AGA-LNS 引入时差插入法改进交叉、变异算子，并嵌入移除、插入算子。针对4 个不同客户规模的算例，AGA-LNS 与AGA 和LNS 相比，求解质量平均改进了2.73%和21.27%，求解时长平均缩短了7.63%和2.13%，求解质量高，收敛速度快，因此AGA-LNS 能较好地求解带混合时间窗约束的车辆路径问题。

（3）不同混合时间窗比例敏感性分析表明，相同客户规模下，硬时间窗客户数量比例越小，配送成本越低；不同车辆行驶速度敏感性分析表明，不同行驶速度对配送计划的制定及配送成本有较大影响，因此在优化配送方案时所设车辆行驶速度应尽量贴近现实。

未来研究将考虑实时交通信息、电动车配送等因素，使问题更贴近实际，并改进、开发更加有效的求解算法。