基于ELM人工神经网络的滑坡失稳预测模型
欧阳高明,宋加平,李 灿,段守荣
(1.广东中灏勘察设计咨询有限公司,广东 肇庆 526060;2.东莞水务集团,广东 东莞 523000)
收稿日期:2022-03-02;修回日期:2022-04-22
作者简介:欧阳高明(1991-),男,本科,工程师,主要从事水利水电工程研究工作。
1 概述
山体崩塌、滑坡、泥石流是全球高山地区广泛分布的三大地质灾害,滑坡是发育最为普遍、破坏最为严重、研究最为集中的一种。通常,滑坡的的发生受到降水、地震、地下水等多种因素共同影响的结果。一般来说,滑坡发生之前都会有明显的变形,但坡体的变形具有典型的非线性特点。鉴于滑坡带来的巨大灾难性和损失,滑坡预测是国内外研究的重点与热点。目前国内关于滑坡的预测主要集中于坡体变形量的追踪与预测。许多学者建立了关于边坡变形预测的数学模型[1-4]。随着计算机和人工智能的发展,采用神经网络对边坡变形的预测成为滑坡灾害预测的主流方法。赵甜[5]基于改进的BP神经网络开展了滑坡危险性评价研究,并给出了滑坡危险性等级划分。高玮和冯夏庭[6]提出了灰色-进化神经网络模型,并在新滩滑坡上进行了验证,表明模型的正确性。周迎等[7]把BP神经网络模型应用于竹溪鲁滩坝滑坡,并得到降雨工况下该类滑坡可能发生局部圆弧形滑移破坏的规律。刘艺梁等[8]采用经验模态分析法与神经网络建立了EMD-BP神经网络模型,实例证明该模型能有效的提高预测精度,适用性较强。赵福军和樊雅婧[9]基于深度卷积神经网络和遥感图像构建了预测模型,并对九寨沟地震诱发滑坡的识别中进行了验证,结果表明,该方法对滑坡体识别的最高精度达87.7%。
目前,采用神经网络对滑坡稳定性进行预测已经取得了一系列进展,也验证了该方法的有效性。但受限于影响滑坡失稳破坏因素较多、成因复杂的特点,既有研究存在一些缺点,如系统性不强和不全面的缺点。基于相关研究的不足,本文建立了回归-ELM神经网络模型,提出了克服参数设定复杂问题的解决方法,建立了一种更为准确的滑坡预测模型。
2 研究原理
2.1 预测模型概述
本文模型包含两个阶段:初步预测阶段和误差修正阶段,具体过程分述如下。
1) 初步预测阶段
初步预测阶段可分为回归拟合和组合预测:首先用MATLAB对数据进行拟合,拟合形式主要有多项式函数和正弦函数;然后采用以中值权重法和方差权重法确定组合权重。具体表示为:
(1)
(2)
式中:
ωQ(i)——中值权重;
E(i)——残差序列期望值;
ωF(i)和V(i)——方差权重和残差序列方差。
把回归拟合中值和方差叠加,进一步得到组合权重,得到第i种回归预测模型累加值p(i),即:
P(i)=ωQ(i)+ωF(i)
(3)
最终组合权值ω(i)可表示为:
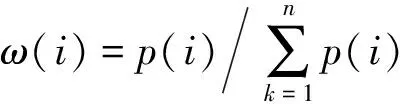
(4)
其中,式(4)是由式(3)得到的最终组合权重值ω(i),其他参数表示意义见上文。
2) 误差修正阶段
利用ELM神经网络进行误差修正以便提高预测精度。根据目前研究,极限学习机能随机产生各层间的连接权值和阈值,具有操作简单、适用性强等优点[10],其过程如下所述:
假设序列中存在n个样本,且满足,xi∈Rn,ti∈Rm,则函数g(x)的极限学习机表示为:
(5)
βi、ωi和oj分别为第i个隐层节点与输层节点间的权值向量、第i个神经元阈值和输出向量。
进一步以零误差逼近训练样本表示为:
(6)
且满足:
(7)
用矩阵表示为:
Hβ=Y
(8)
式中:
H——极限学习机常数矩阵。
综合以上分析,本文首先通过实例验证实测序列样本预测结果的有效性,在此基础上对实测结果进行外推,对边坡的未来发展趋势进行评价和判断。
2.2 趋势判断方法概述[11-12]
1) 秩相关系数检验
秩相关系数检验需样本个数大于4,如果将边坡变形序列表示为Y={Y1,Y2,…Yn},按照从大到小排列为X={X1,X2,…Xn},进一步得到变形序列的秩:
(9)
式中:
N——样本数;
rs——秩。
进一步,如果|rs|
当|rs|>Wp且rs>0时,证明变形趋势恶化,变形增大;
当|rs|>Wp且rs<0时,证明变形趋势稳定,变形减弱。
2) Mann-Kendall趋势检验
将滑坡变形序列进行抽样分析,且样本数不小于10,在零假设条件下,统计序列可表示为:
(10)

(11)
式中:
S和Xi——初步统计量和评价序列在i个节点处的值。
Mann-Kendall趋势检验的最终评价指标Z表示为:
(12)
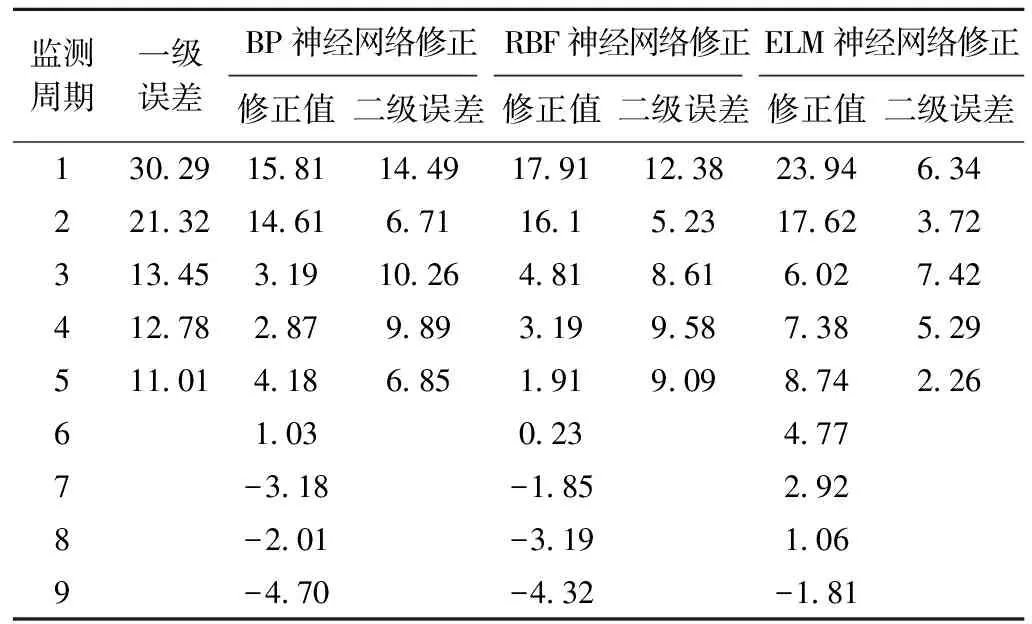
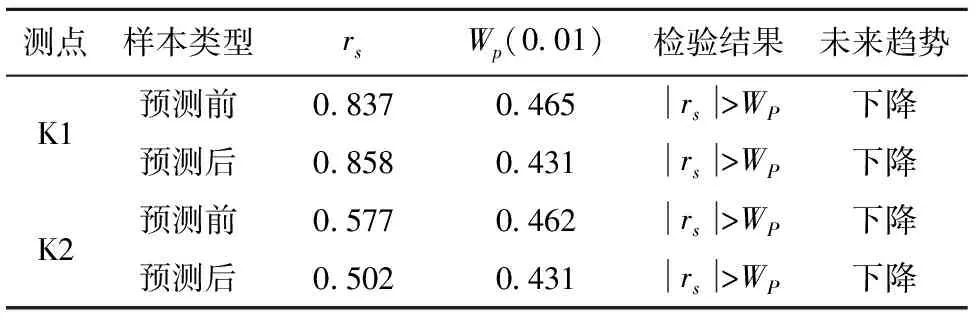
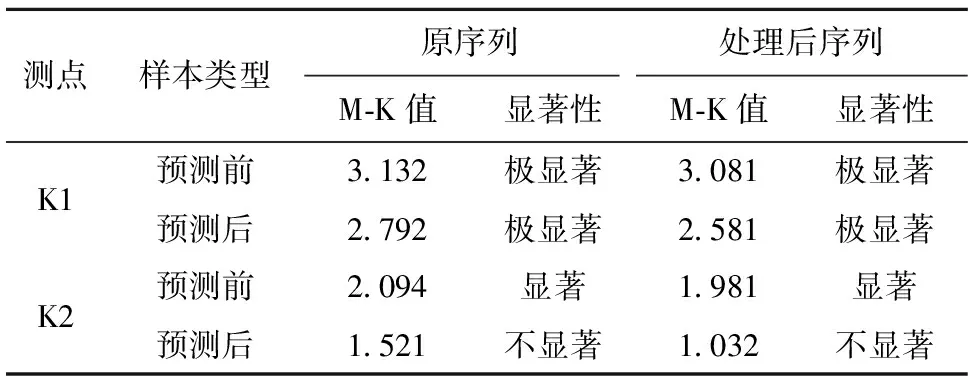
当Z>Z1-a/2时,变形增大;当Z 以上给出了如何判断结果是否符合实际情况的方法。此外,实际滑坡变形的位移是持续增大的,因此,在判断滑坡变形趋势过程中,进一步引入位移变化速率作为评价序列进行建模。 以一典型水库诱发的堆积层滑坡为例,该滑坡基岩主要包括页岩、砂岩和砾石等,根据现场调查,滑体厚度介于10~34 m。钻孔揭示,滑面为基覆界面。研究区的地下水主要靠降水补给,受降水影响很大。孔隙水主要贮存于滑体内,基岩裂隙水主要存在于基岩中,含水层具有路径短,排泄条件差的特点。该滑坡的变形主要受库水位的变动影响,根据现场调查,在蓄水期间,中部产生4条长度介于60~80 cm的大裂缝,总体走向为NW-SN。在水库运营期间,滑坡变形一直在恶化。为及时掌握坡体变形动态特征,及时采取防治措施手段,对该滑坡进行了地表和深部位移监测,本文选取具有代表性的K1和K2进行建模和分析(实时监测结果见图1)。 图1表明,随着时间的增长,边坡位移这逐渐增大,K1监测点最终位移为385 mm,而K2最终位移值为424 mm,且两监测点位移仍有增大的趋势,因此,对该边坡位移进行预测是必要的。 图1 滑坡位移实时监测示意 图2汇总得到两个监测点的位移变化速率示意,结果表明,K1监测点速率最大值为64.7 mm/月,K2监测点速率最大值为42.8 mm/月,平均速率分别为14.82 mm/月和16.3 mm/月;此外,K1监测点的变形速率波动比K2大。 进一步将变形速率进行4个区间(I~IV)划分为: Qi=[Si,Si+1] (i=1,2,3,4,5) (13) S1为最小变形速率;S5为最大变形速率;S3为平均变形速率;S2为S1与S3的均值;S4为S3与S5的均值。 图2 滑坡变形速率示意 汇总结果得到监测点变形速率区间分布(如图3所示)。结果表明,区间Ⅰ的分布比例最大,证明其变形速率较小。滑坡的变形表现为渐进性破坏特征。 前文已经构件了预测模型,本节对监测点变形进行预测,首先基于MATLAB进行初步预测,最终得到拟合曲线见表1。采用二次函数以及正弦曲线的公式进行拟合表明,拟合优度均大于0.96以上,其值分别为0.979、0.982、0.993和0.976,说明拟合效果较好,结果较合理。此外,拟合结果发现K2的多项式拟合效果最佳。 表1 初步预测拟合 计算得K1和K2两侧点的3种组合权值为: 根据以上公式采用期望权值法、方差权值法和叠加权值法,进一步获取得本文的初步预测结果。采用对平均绝对误差及方差两者进行归一化条件叠加处理,进而得到综合指标。用该指标即可进行精度和稳定性评价的综合分析(值越小证明结果越精确),最终得到的结果见表2和表3。 表2 K1初步预测结果评价指标 表3 K2初步预测结果评价指标 由表2和表3可知,采用组合模型预测的指标(平均绝对误差、方差和综合指标)较单项预测指标小,说明采用组合方法能够显著提高预测精度。在组合预测中,叠加组合的预测效果最好,因此叠加模型方法的实际预测能力适用性最好。此外,实测变形数据与初步预测结果对比,获取初步预测误差序列,使用极限学习机对该序列进行误差修正,最终结果汇总于表4和表5。修正结果表明,BP网络神经修正、RBF网络神经修正和ELM网络神经修正中,最后一种修正方法的二级误差最小,说明修正效果最好。 表6汇总得到滑坡变形预测的最终结果,由表6可知,K1和K2两测点的相对误差值都比较小,其中K1测点的相对误差均值为-0.62%,K2测点的相对误差均值为1.89%,证明预测结果比较可靠。同时进一步对该两测点未来变形进行预测发现,K2监测点变形持续增大,K1增加幅度较小。 表4 K1初步预测误差修正 mm 表5 K2初步预测的误差修正 mm 表6 滑坡变形综合预测 mm 进一步采用Mann-Kendall趋势检验和秩相关系数检验变形趋势进行分析,将分析过程分为预测前的趋势检验和预测后的趋势判断。最终得到滑坡变形速率序列的检验结果汇总于表7。结果表明,K1和K2在预测前和预测后的两个阶段均存在|rs>WP,这证明两测点在各阶段变形趋势均增大,滑坡变形持续恶化。此外,预测前的rs值大于预测后,说明外推预测后滑坡变形趋势有所减慢。最后,K1的rs值比K2要大,证明前一个点的变形趋势要大于后一个监测点。表8为采用Mann-Kendall趋势检验的汇总结果,结果表明与原序列的M-K值相比,处理后的序列M-K值有所减小,证明处理结果存在相关性。此外,预测前后阶段的M-K值均大于0,但显著性有所不同。其中K1点在预测前均为极显著,而K2点在预测前和预测后为显著和不显著两种结果。 表7 秩相关系数检验 对比采用两种不同检验方法对样本数据的预测前和预测后两阶段的检验结果可知,检验结果非常类似,通过两种方法也互相印证了结果的可靠性。其中采用秩相关系数检验的结果均为|rs|>WP,且未来趋势均为下降。两种趋势检测结果均表明,前文预测分析的可信度较高,研究区滑坡的未来变形趋势存在继续增大的可能性,在实际应用中应采取一定的防范措施。 表8 Mann-Kendall趋势检验 1) 滑坡的变形预测对于及时掌握滑坡变形动态是很重要的,本文建立神经网络模型对滑坡的变形预测结果表明,组合预测结果的精度要显著大于单项预测的准确性,另外,合理确定权值对于获取准确结果有比较大的影响,本文采用的叠加组合权值更为合理。 2) 秩相关系数和Mann-Kendall趋势检验对某滑坡实例变形预测表明,滑坡仍然有增大的趋势,其中K1测点增长的趋势更强,且与实测变形预测的结果最吻合。 3) 传统的神经网络对于误差修正能力有限,而本文采用的极限学习机较传统方法而言,结果更准确,操作更简单。3 实例分析
3.1 工程概况
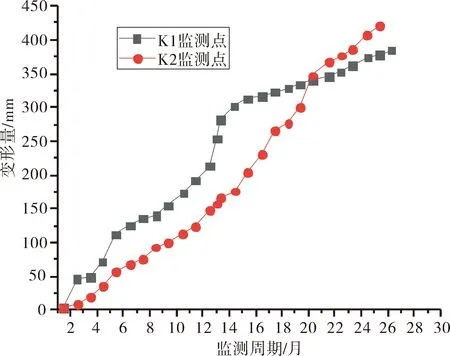
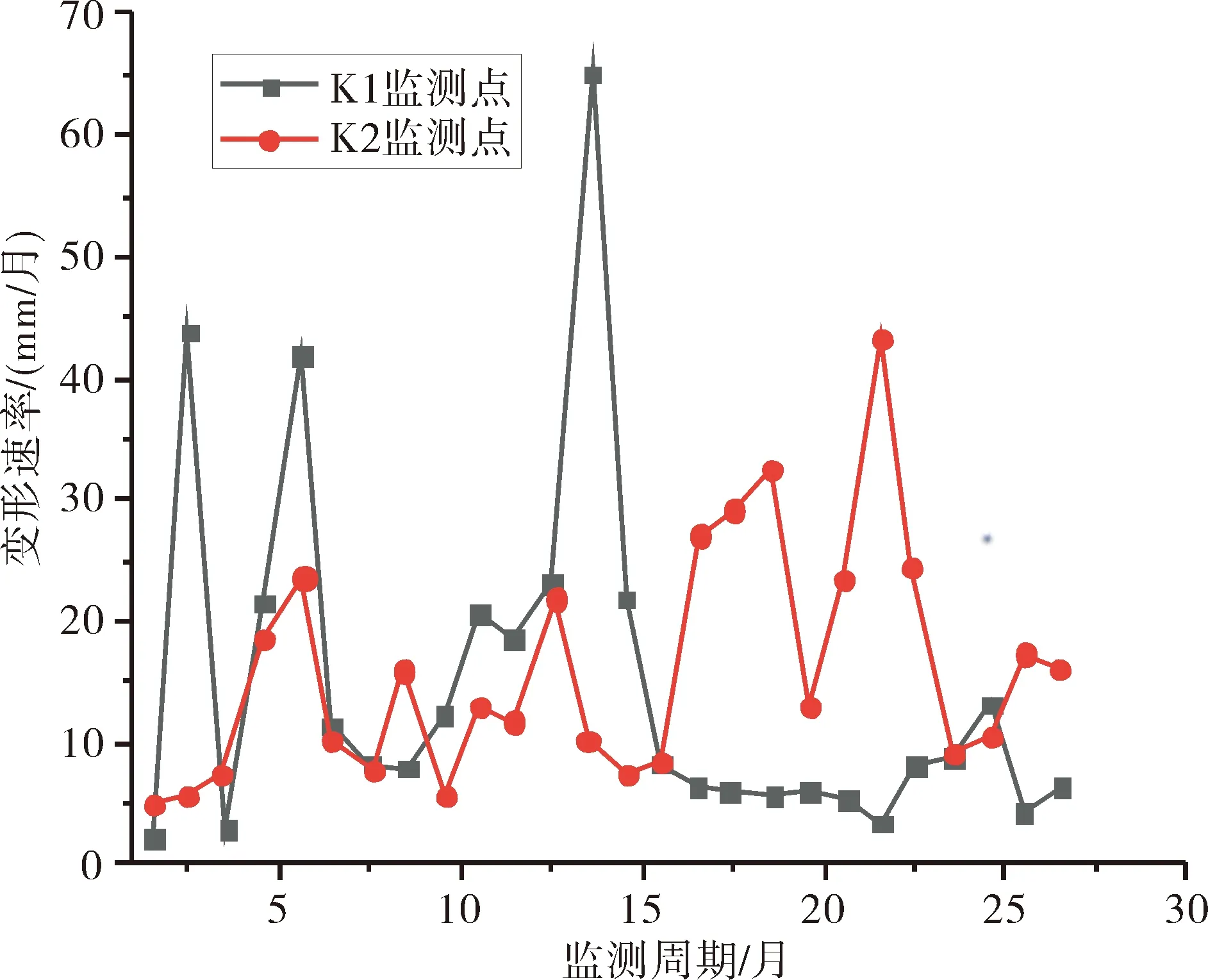
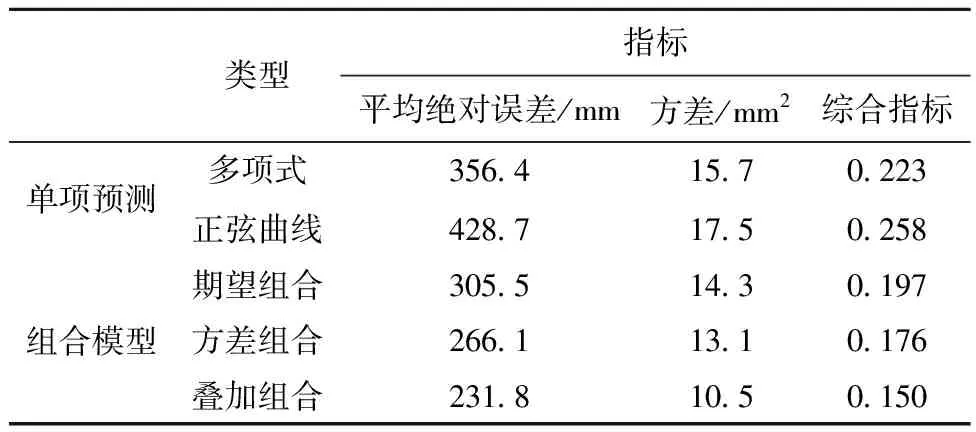
3.2 变形预测分析






3.3 变形趋势分析
4 结语

