属性权重未知情况下犹豫模糊多属性决策方法
申情,蒋云良,张雄涛
(1.湖州学院 理工学院,浙江 湖州 313000;2.湖州师范学院 信息工程学院,浙江 湖州 313000;3.湖州师范学院 浙江省现代农业资源智慧管理与应用研究重点实验室,浙江 湖州 313000)
多属性决策是有广泛应用背景的一类决策。但由于客观事物既有确定性一面又有不确定性一面,使得这一类决策问题通常受种种不确定性的困扰,决策者会因此在决策时产生一定的犹豫性,这使得Torra 等[1-2]的犹豫模糊集(hesitant fuzzy set,HFS)理论应运而生。HFS 理论允许元素属于集合的隶属度可以是若干个犹豫模糊值,一定程度上发展了Zadeh 模糊集理论,吸引了不少学者基于HFS 理论研究犹豫模糊环境下的多属性决策问题。Xia 等[3]最早给出犹豫模糊集的数学表达式。在中国,张超等[4]研究了犹豫模糊图及其在多属性决策中的应用,武文颖等[5]给出了基于概率犹豫信息集成方法的群决策模型,王宝丽等[6]提出基于粒计算给出未知属性权重时的犹豫模糊多准则决策方法[7-10]等。集对分析理论能同时表示系统的确定性测度与不确定性测度以及两者之间的关系,把人们对事物的确定性与不确定性关系的辩证认识转换成一个具体的数学工具-联系数。集对分析自赵克勤[11]于1989 年提出以来,已在人工智能和不确定性决策中得到应用[12-17]。文献[18]针对准则权系数信息不完全确定的多准则直觉模糊决策,将直觉模糊数转化为二元联系数,建立了基于二元联系数的多准则直觉模糊决策综合加权模型。文献[19-20]研究了区间数和联系数之间的关系,分别提出了准则值和准则权重为区间数的多准则决策方法。文献[21-22]中针对二元联系数信息的集成问题,定义了几种二元联系数信息集成的几何算子,提出了基于二元联系数的信息不完全的群决策方法。文献[23]通过将三角模糊数转化为二元联系数,提出了一种基于三角模糊数的二元联系数双重多属性决策方法。文献[24]将不确定语言变量转换为二元联系数,利用二元联系数的距离公式,建立了多目标规划模型。文献[25-26]利用二元联系数方法解决了区间直觉模糊多属性决策和犹豫模糊多属性决策问题。
本文利用犹豫模糊元边界的确定性与边界内隶属度取值的不确定性,把同样具有确定性与不确定性双重特性的集对分析理论中的三元联系数引入到属性权重未知的犹豫模糊多属性决策研究,建立了属性权重未知情况下的基于三元联系数的犹豫模糊多属性决策新模型,该新模型不仅包含了其他模型的结果,还提供了其他可能的方案排序结果,由此形成的有条件决策,是犹豫模糊多属性决策不确定性本质属性的映照,与犹豫模糊多属性决策实际应用情况吻合,且算法简明;此外,在第5 节还介绍了经典势函数shi(μ)的扩展公式,使得本文给出的新模型有更好的潜力应对更为复杂的犹豫模糊多属性决策问题。
1 权重未知的犹豫模糊多属性决策
1.1 犹豫模糊集
犹豫模糊集的基本特征在于用多个隶属度刻画给定元素对于给定集合的隶属程度。例如,3 位科技专家在评估某科技项目创新程度时分别给出0.65、0.75、0.8 三个隶属度,这3 个隶属度用<0.65,0.75,0.8>表示,称之为犹豫模糊元。犹豫模糊元是犹豫模糊集理论的核心,一般用hA(x)表示一个犹豫模糊元,定义如下。
定义1设X是一个非空集合,从集合X到[0,1]区间上的一个函数称为犹豫模糊元(hesitant fuzzy element,HFE)。Xia 等给出的犹豫模糊集的数学表达式为

式中:x代表某一属性;hM(x)表示方案M对属性x的隶属程度,也称综合犹豫模糊元,它是方案M在n个属性上的n个犹豫模糊元hA(x)(A=1,2,···,n)的综合值。
Torra 给出犹豫模糊元的计算公式[2]:

其中:h、h1、h2是3 个犹豫模糊元。
熟悉模糊数学的人知道,对于两个和两个以上模糊隶属度作“取大取小”运算会丢失信息和导致误判。同理,对于两个和两个以上犹豫模糊元作“取大取小”运算也会丢失信息和导致误判。因此,如何科学地提取一个犹豫模糊元的犹豫模糊信息,又为后续的数学建模运算与决策提供方便,显然是犹豫模糊多属性决策研究的关键问题。
1.2 权重未知的犹豫模糊多属性决策问题
在犹豫模糊多属性决策问题中,属性权重对决策起着举足轻重的作用。通常,在给定的一个模糊多属性多方案决策问题中,属性权重由专家根据自身的知识和经验给定,但专家定权会有一定的主观性,简称主观定权;与主观定权法相反的有“客观定权法”,这是根据原始数据之间的关系来确定权重。在同一个多属性决策问题中,如何客观地给多个属性确定权重,是一个复杂的问题;为了界定本文要研究和解决的问题,下面对权重未知的犹豫模糊多属性决策问题先作一般性描述:设有四元组D=(S,Q,W,P)表示一个犹豫模糊多准则决策系统,其中S为评价对象集S=(S1,S2,···,Sm),m≥2;Q为评价属性集Q=(Q1,Q2,···,Qn),n≥2;且Q1,Q2,···,Qn都是越大越好的效益型属性;W为属性权重集为评价函数P=f(S×Q)∈[0,1]。
要求在未知(w1,w2,···,wn)具体数值,但条件下,决断出S中的最优对象,并作出S中m个对象的优劣排序。
当评价函数P为犹豫模糊元时,属性权重未知的犹豫模糊多属性决策问题可以进一步描述如下:
设有m个备用方案 (S1,S2,···,Sm),每个方案各有n个相同的属性 (Q1,Q2,···,Qn),但对每个属性的评价函数Pkt(k=1,2,···,m;t=1,2,···,n)不同,且用犹豫模糊元hp(xkt)=(xkt1,xkt2,···,xktn)表示,属性权重但w1,w2,···,wn具体数值未知,为方便,约定各属性都是越大越好的效益型属性,要求在m个备用方案中决策出最优方案,并对这些方案在犹豫模糊环境下的优劣排序作犹豫模糊性分析。
不难看出:属性权重未知的犹豫模糊多属性决策问题比属性权重已知的犹豫模糊多属性决策问题更为复杂。
2 三元联系数
2.1 基于犹豫模糊元的三元联系数定义
三元联系数是集对分析理论中的一种结构函数,也称同异反联系数,其一般形式为µ=a+bi+cj,但对应于不同的“反”有不同的类型,如“正负型‘反’(j=−1,i∈[−1,1] )”“有无型‘反’(j=0,i∈[0,1])”等;为了把三元联系数用于未知属性权重的犹豫模糊多属性决策研究,重作定义:
定义2设hA(x)=(x1,x2,···,xn)是一个犹豫模糊 元,0 称µ=a+bi+c j,i=[0,1],j∈[−1,0]为基于犹豫模糊元的三元联系数,或称犹豫模糊元联系数,也简称三元联系数。 一般式为 式中:a∈[0,1],b∈[0,1],c∈[0,1],i∈[0,1],j∈[−1,0],i称为犹豫模糊元联系数中偏于肯定的犹豫模糊强度系数,j称为犹豫模糊元联系数中偏于否定的犹豫模糊强度系数。统称i、j为犹豫模糊强度示性系数,简称示性系数。 以上定义的三元联系数具有以下性质。 性质1与犹豫模糊元具有等价性。 证明根据定义2 和式(5)可知,当三元联系数中的示性系数i,j取适当的数值时,可以得到由式(1)定义的犹豫模糊元中任意一个隶属度,例如前面提到的犹豫模糊元hA(x)=(0.65,0.75,0.8),由此按定义2 得到犹豫模糊元三元联系数 性质2系统性。 证明首先,式(5)所示三元联系数具有整体性,这是因为相对于犹豫模糊元hA(x)=(x1,x2,···,xn),多了hA(x)的补集也就是,有hA(x)=cj,hA(x)=a+bi。 根据系统是由两个或两个以上要素组成的有机整体的定义,可知式(5)所示三元联系数是一个系统,所以具有系统性。 其次,三元联系数的系统性还体现在3 个联系分量a,bi,cj的层次性,这种层次性由3 个联系分量的示性系数1,i,j得到充分体现,因为i∈[0,1],j∈[−1,0]。 再次,在µ=a+bi+c j中a、bi、cj存在相互作用,例如当i、j有具体数值时,会对a起增减作用。 第四,不确定性。不仅i∈[0,1],j∈[−1,0]在各自的定义区间取哪一个具体数值具有不确定性,而且当i在[0,1]取定某个具体的数值时,是加大a还是减小c也具有不确定性;同理,当j在[-1,0]取定某个具体的数值时,是减小a还是减小b也具有不确定性。 显然,上述不确定性说明了式(5)所示三元联系数不仅是一个不确定性系统,也同时说明应用三元联系数解决不确定性多属性决策问题时与实际不确定性环境的对应性与灵活性。 性质3可比较性。 证明情况1,示性系数效应结果比较。根据定义2,易知 成立。 情况2,示性系数有确定值时的结果比较。由情况1 进一步推知,当两个三元联系数 µ1=a1+b1i1+c1j1与 µ2=a2+b2i+c2j中的i1,j1与i2,j2各有确定的值时,µ1与 µ2能比较大小。 例如对于三元联系数 µ1=0.6+0.3i1+0.1j1与µ2=0.5+0.25i2+0.25j2,当i1=0.3,j1=−0.5,i2=0.8,j2=−0.1 时,有 µ1=0.6+0.09−0.05=0.64,µ2=0.5+0.2−0.025=0.675 。显然,这时有 µ2>µ1。 情况3,同异反联系分量几何合成结果比较。把三元联系数µk=ak+bkik+ck jk(k=1,2,···,n)映射到“同异反”三维空间见图1,计算三元联系数的“模”: 根据“模”rk的大小关系确定n个三元联系数µk=ak+bkik+ck jk的大小关系。其原理是把三元联系数看成是一组三维向量,在“同异反犹豫模糊决策”空间中求这三组三维向量的合成,见图1。 图1 同异反犹豫模糊空间中的同异反犹豫向量合成示意Fig.1 Synthesis of identical discrepancy contrary vectors in identical discrepancy contrary hesitant fuzzy space 从图1 看出,三元联系数a+bi+cj的“模”是正向(肯定的)确定性测度a与负向(否定的)确定性测度c和不确定的犹豫测度bi在i=1时的一种几何合成。 情况4,与完全非犹豫点的距离比较。 定义3由定义1 和定义2,可以进一步称犹豫模糊元三元联系数为 µhA(x)=1+0i+0j在图1 所示同异反犹豫模糊决策空间中的点为完全肯定点(完全非犹豫点),记为 µ(1,0,0),见图2。 图2 同异反犹豫模糊决策空间中完全非犹豫点Fig.2 Completely non-hesitant point in identical discrepancy contrary hesitant fuzzy space 计算任意一个非完全不犹豫点µk=ak+bki+ck j(k=1,2,···,n) 与完全非犹豫点 µ(1,0,0)的海明距离ρ,即 当有m个非完全不犹豫点时,可以根据它们与完全肯定点(完全非犹豫点)µ(1,0,0)的距离大小作出肯定程度的比较,与 µ(1,0,0)距离小的要比与µ(1,0,0)距离大的肯定。 情况5,势函数比较。 定义4当犹豫模糊三元联系数µ=a+bi+c j中的ck不是零时,定义a/c为犹豫模糊三元联系数µ=a+bi+c j的势函数,记为 利用势函数可以比较两个犹豫模糊三元联系数势的大小。 根据集对分析理论,三元联系数可以作普通的加减乘除四则运算,但本文仅用到其中的加法运算和乘法运算,定义如下: 定义5设 µ1=a1+b1i+c1j,µ2=a2+b2i+c2j是两个三元联系数,则它们的和是一个三元联系数µ=a+bi+c j,记作 式中:a=a1+a2,b=b1+b2,c=c1+c2。 从定义5 看出,三元联系数的加法运算满足交换律,对于三个和更多个三元联系数相加满足结合律。 定义6设 µ1=a1+b1i+c1j,µ2=a2+b2i+c2j是两个三元联系数,则他们的乘积是一个三元联系数µ=a+bi+c j,记作 式中:a=a1a2+c1c2,b=b1a2+b2a1+b1b2+c1b2,c=a1c2+b1c2+a2c1,示性系数i,j在以上运算过程中的规则是ii=i,ij=j,j j=1。 从定义6 看出,三元联系数的乘法运算满足交换律,对于三个和更多个三元联系数相乘满足结合律。 定义7一个不等于零的实数k(k≠0)与三元联系数 µ=a+bi+cj相乘,其积仍然是一个三元联系数。记作 1)将决策者对各方案在每个属性下的评价值进行数学表达形式转换。应用式(2~5)把专家给出的各属性评价值犹豫模糊元转换成三元联系数形式。 2)利用式(6),即三元联系数 µ=a+bi+cj的势函数 shi(µ)计算公式,计算1) 中得到的各三元联系数的势函数值。 3)利用基于离差的属性权重计算公式计算各属性权重: 4)利用综合加权求和计算公式计算各评价对象的综合三元联系数: 5)犹豫性分析。利用犹豫示性系数i,j取不同值时各评价对象的三元联系数值,讨论犹豫性对初排序的影响。 6)给出决策建议。根据以上5 步结果,提出决策建议,说明在何种犹豫模糊条件下的最优方案及其他方案的优劣排序。 为便于作对比分析,以下用2 个实例来验证本文前述模型的有效性。其中实例1 取自文献[6],实例2 取自文献[27]。 实例1某企业为选拔一重要部门优秀管理人员,需要作多属性决策。企业负责人根据2 位专家的建议,从5 位备选管理人员u1~u5中根据专业技能c1、理性技能c2、人际交往技能c3和设计技能c4四个方面选择1 位部门经理。各个考核准则权重未知。一方面,由于两位专家来自不同部门,对各个备选人员在不同属性上的模糊评判可能不同,即产生犹豫模糊判断值;另一方面,可能有专家对部分备选人员在一些属性上的表现把握不准或了解不够,从而出现不能给出模糊值的情况,如人力资源部门的管理人员对备选人员u1的人际交往技能c3方面了解不够,因此未做出评价,仅有本部门2 个评估专家给出的模糊判断值0.5。2 位专家对备选人员的判断评价信息如表1 所示。试给出5 个排序对象的优劣次序。 1) 根据式(2)、(3)、(4)、(5) 把表1 中的各个犹豫模糊元改写出成三元联系数的形式,得表2。 表1 犹豫模糊决策系统Table 1 Hesitant fuzzy decision making system 表2 用三元联系数表示的犹豫模糊决策系统Table 2 Hesitant fuzzy decision making system expressed TCN 2) 利用三 元联系 数 µ=a+bi+c j的势函 数shi(µ)计算公式式(6),计算表2 中各三元联系数的势函数值,得表3。 表3 一个犹豫模糊决策系统三元联系数的势函数Table 3 Potential function of TCN in a hesitant fuzzy decision making system 3)利用式(7),得到各属性权重为 4)利用式(8),计算得u1、u2、u3、u4、u55 个评价对象各自的综合三元联系数: 5)犹豫性分析。 分别考察犹豫示性系数i、j取不同值时的5 个评价对象的三元联系数值,并给出优劣排序,结果见表4。 表4 优劣排序比较Table 4 Comparison of ranking 6)决策建议。 首先,从表4 看出,无论是在哪一种犹豫情况下,u4最好。其次,由表4 看出,5 个评价对象在i=0,j=0 时的排序与文献[6]得到的5 个评价对象排序相同,提示文献[6]所用到的算法并没有从实质上计及决策者的犹豫模糊性;表4 第3 列到第7 列在计及决策者的犹豫模糊性之后,显示出这5 个评价对象的优劣排序跟随犹豫强度变化而变化,这符合犹豫模糊决策实际。 实例2某企业董事会的5 名成员计划制定未来5 年内的战略计划。假设有4 种可能的方案Yi(i=1,2,3,4)要进行评估。选择其中最重要的项目,并从其重要性的角度进行排序,考虑如下4 个属性:G1财务支出,G2客户满意度,G3内部业务流程,G4学习与成长前景。企业董事会成员对各方案在不同属性下的评估值如表5 所示。 表5 犹豫模糊决策信息表Table 5 Hesitant fuzzy decision information table 1)根据式(2)~(5)将表6 中专家对各个属性的评估值改写出成三元联系数的形式,得表6。 表6 用三元联系数表示的犹豫模糊决策信息表Table 6 Hesitant fuzzy decision information table expressed by TCNs 2)利用三元联系数的势函数 shi(µ)计算公式,计算表6 各三元联系数的势函数值,得表7。 表7 犹豫模糊决策信息中三元联系数的势函数Table 7 Potential function of TCN in hesitant fuzzy decision making information 3)根据式(7)计算得各属性权重为 4) 利用式(8) 计算出各方案的综合三元联系数: 5)犹豫性分析。 计算犹豫示性系数i,j取不同值时4 个方案的三元联系数值,并给出优劣排序,结果见表8。 表8 4 个方案的优劣排序比较Table 8 Comparison of the ranking for four schemes 6)决策建议。从5)中看出,当4 个方案联系数中的i和j同步取值时(同步犹豫),Y4最好。这与文献[27]中的决策建议一致。但是不同步取值(不同步犹豫)时,每个方案都有可能成为最优。 本文把集对分析中的三元联系数用于属性权重未知的犹豫模糊多属性决策研究,核心工作是把犹豫模糊元转换成三元联系数 µ=a+bi+cj,继而利用三元联系数的势函数 shi(µ),按“离差最大法”计算得到各属性的权重,为处理未知属性权重的犹豫模糊多属性决策问题提供了一个新途径。实例应用表明,这一新思路可行且有效,其有效性首先源自把犹豫模糊元hA(x)转换成三元联系数µ=a+bi+ci的过程,较为系统地保留了的犹豫模糊信息;其次是建立基于三元联系数的犹豫模糊多属性决策模型;三是从不同角度和不同算法提取三元联系数的系统信息;四是就各方案的各属性加权综合后的三元联系数 µ(uk)作不同犹豫模糊强度下的不确定性分析,在数值上重现出犹豫模糊不确定性在决策空间中的真实犹豫模糊图景,从而保证了模型计算结果对各种犹豫模糊情况的总体覆盖,保证了犹豫模糊不确定性决策建议的客观合理性和科学性。从系统科学的角度看,本文介绍的基于三元联系数 µ=a+bi+c j的属性权重未知的犹豫模糊多属性决策模型,其有效性来自三元联系数系统地利用了问题给出的犹豫模糊结构信息。 犹豫模糊条件决策是本文提出的一个新概念。从数学的角度看,犹豫模糊多属性决策是一类在犹豫模糊空间中展开的决策,这个空间本身具有犹豫模糊性,犹豫模糊多属性决策系统是该空间中的一个有限子空间,这个有限子空间与周围的空间有着信息的交换,所有这些信息构成了犹豫模糊决策条件集;显然,在犹豫模糊空间中展开的犹豫模糊决策,本质上离不开这些犹豫模糊条件的约束,这是犹豫模糊条件决策的空间几何解释。本文给出的基于三元联系数的犹豫模糊多属性决策模型则是犹豫模糊条件决策的一种简化了的数学模型,模型中的犹豫模糊示性系数i、j如实地把不同犹豫模糊条件下的犹豫模糊强度信息传递给有关决策参数,化解了由“犹豫”和“模糊”两类不确定因素叠加而致的复杂性,在保证模型计算结果客观合理的同时又让算法具有经济性、简明性和实用性。 另一方面,“犹豫模糊条件决策”也将是一个会引发争鸣的概念。因为,从犹豫模糊多属性决策文献[4-10]和文献[27]看,这些文献介绍的工作都是通过某种算法得到唯一确定的计算结果,进而给出基于这一确定的计算结果的决策建议。由此引出一个值得深思的问题:面对一个犹豫模糊多属性决策问题,研究结果是给出一个唯一确定的决策建议好,还是给出不同犹豫模糊强度条件下的决策建议集好。这需要有关犹豫模糊决策研究人员深思,也需要大量的决策实践检验。 本文把集对分析中的三元联系数用于属性权重未知的犹豫模糊多属性决策研究,发现基于三元联系数的属性权重未知的犹豫模糊多属性决策模型的计算结果中,不仅包括了同一个属性权重未知的犹豫模糊多属性决策问题用粒计算得到的结果,还得到其他的方案优劣排序,真实地映照出属性权重未知的犹豫模糊多属性决策系统在犹豫模糊多属性决策空间中与犹豫模糊环境进行犹豫模糊信息交换,影响到决策结果的真实图景;文章对犹豫模糊环境中的“犹豫模糊条件决策”概念作出了几何解释和数量化解释;还介绍了三元联系数经典势函数 shi(µ)的扩展公式,使得本文给出的模型有更好的适用性;当然,作为一种新的属性权重未知的犹豫模糊多属性决策方法,仍然需要有更多的实例验证和决策实践检验,也需要在形式化和程序化处理上作进一步研究,以便于用计算机处理此类问题,这也是下一步的工作。








2.2 三元联系数的运算



3 算法步骤

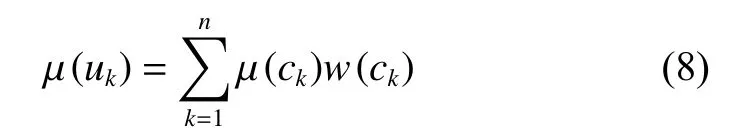
4 应用实例












5 讨论
5.1 模型的有效性
5.2 关于势函数


5.3 关于犹豫模糊条件决策
6 结束语

