串联工业机器人两级定位误差标定方法研究

乔贵方，田荣佳，张 颖，王保升，宋光明，宋爱国

(1. 南京工程学院自动化学院，江苏 南京 211167; 2. 东南大学仪器科学与工程学院，江苏 南京 210096;3. 南京工程学院 智能制造装备研究院，江苏 南京 211167)

0 引 言

《中国制造2025》以智能制造为主攻方向，该计划中指出将大力推动机器人和高档数控机床等重点领域的发展[1]。工业机器人作为智能制造装备的代表，其应用领域也随着技术的快速发展而逐渐扩展。丁汉院士团队[2]及廖文和教授团队[3]等近些年将工业机器人应用于大型复杂曲面叶片智能磨抛作业以及大型复杂零件制孔、铆接、装配等高端制造领域。欧洲的COMET项目指出工业机器人的绝对定位误差需优于 0.05 mm才能够满足机械加工作业的精度要求[4]。2017年科技部实施的“智能机器人”重点专项中指出工业机器人的绝对定位误差在叶片磨抛、飞机钻铆等作业中应优于0.05 mm，而目前工业机器人绝对定位精度仍无法满足该要求。

机器人标定技术是目前用于提升工业机器人绝对定位精度的主要手段之一[5-6]。机器人的关节误差、运动学模型误差、变负载情况下的刚度误差以及关节迟滞等误差因素均影响其精度性能。根据是否建立误差模型，将机器人标定方法分为模型标定法和非模型标定法[7]。其中模型标定法又分为轴线测量法和误差模型法。轴线测量法通过逐一旋转机器人关节，并使用激光跟踪仪等设备测量机器人的关节旋转轴线，进而建立关节坐标系，最后计算得到运动学模型参数。J. Santolaria等基于轴线测量法将KUKA KR-5 机器人的位置误差从0.40 mm降低为0.11 mm[8]。误差模型法的基本步骤分为误差建模、误差测量、参数辨识和误差补偿。目前机器人的运动学模型主要有经典的DH模型[9]、M-DH模型[10]、POE模型[11]、零参考模型[12]等。目前常用的误差测量设备有视觉测量[13]和激光跟踪仪[14]等。根据误差模型所包含信息不同，主要分为位置误差模型、位姿误差模型和距离误差模型[7]，其中距离误差模型无需进行参考坐标系转换，但从精度性能的提升效果上，基于位姿误差模型的提升效果最好。乔贵方等基于位姿误差模型将TX60机器人的位置误差从0.54 mm降低到0.08 mm[15]。与轴线测量法相比，误差模型法的标定精度更高，但具有区域性。温秀兰等结合了轴线测量法和误差模型法，将埃夫特ER10L-C10机器人的平均定位误差从2.068 mm降低至0.236 mm[16]。

基于非模型的误差标定方法无需建立机器人误差模型，主要是通过插值或神经网络等方法进行位姿误差拟合和预测。相比于基于模型的误差标定方法，基于非模型的误差标定方法能够更好地处理一些无法建模的误差因素。李宇飞等提出了基于反距离加权的空间插值方法，将机器人绝对定位误差由1.307 mm降低为0.156 mm[17]。Bai Y等通过模糊插值方法将PUMA 560机器人的误差降低了98%[18]。Cai Y等利用克里金插值算法将KR210机器人的最大位置误差从1.307 3 mm降低为0.314 8 mm[19]。Li B等提出GPSO优化的BP神经网络预测工业机器人定位误差，将空载机器人的定位误差降低了77.6%[20]。

本文针对串联型工业机器人的精度性能提升方法展开研究，提出了一种融合误差模型标定方法和基于RBF神经网络拟合的两级标定方法，并通过实验验证了该标定方法的性能。

1 工业机器人标定平台构建

本文采用激光跟踪仪Leica AT960和串联工业机器人Staubli TX60构建串联工业机器人标定平台如图1所示。激光跟踪仪Leica AT960的测量不确定度为±(15 μm+6 μm/m)，待标定的工业机器人Staubli TX60的重复定位精度为±0.02 mm，激光跟踪仪的测量靶标T-MAC通过转接板安装在工业机器人Staubli TX60的末端法兰盘上，激光跟踪仪与被测靶标的测量距离小于2 m，配套使用的测量分析软件为Spatial Analyzer。其名义DH模型的参数值如表1所示。

图1 串联工业机器人标定平台

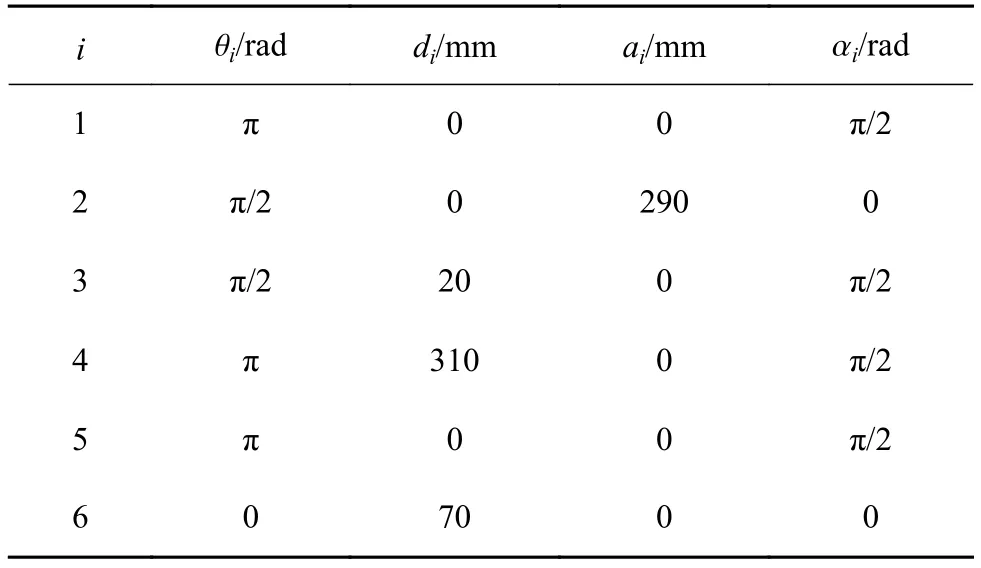
表1 Staubli TX60机器人DH运动学模型参数的名义值

本文依据ISO 9283及GB/T 12642—2013标准实施Staubli TX60机器人的末端定位误差测量[21]。以机器人的基坐标系作为参考坐标系，以坐标值(550，0，550)为中心点，在机器人的前方运动空间内随机选择1 000个测量点用于本文的运动学参数标定和方法效果验证。

2 基于位姿误差模型的工业机器人运动学参数辨识

2.1 基于M-DH的运动学误差模型建立

DH 模型利用运动学参数ai、di、αi和 θi描述了机器人构型，关节i的齐次变换矩阵如下式所示：

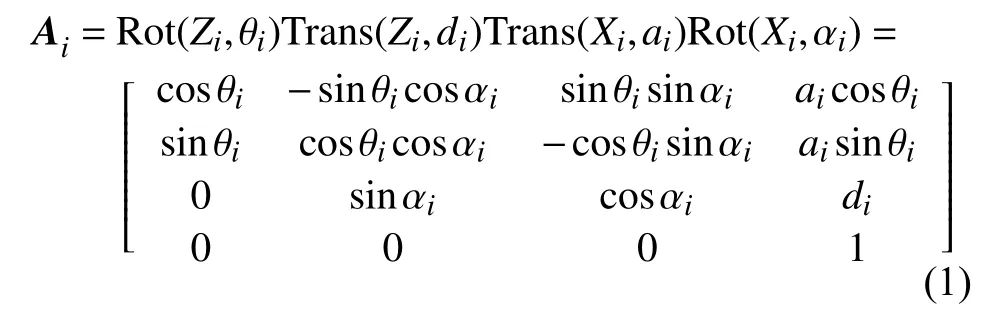
其中i为机器人的关节序号，i=1,2 , ···,6。

当工业机器人的相邻两轴平行或接近平行时，DH模型存在奇异性问题，S. Hayati等提出在DH模型基础上添加一个绕Y轴旋转的关节扭角βi描述相邻平行轴的位置关系[10]，如图2所示。机器人关节i的齐次变换矩阵变为式(2)。由于关节2与关节3的轴线向量理论上是平行关系，因此，运动学参数d2=0，β2=0，其余关节的运动学参数βi均为0。

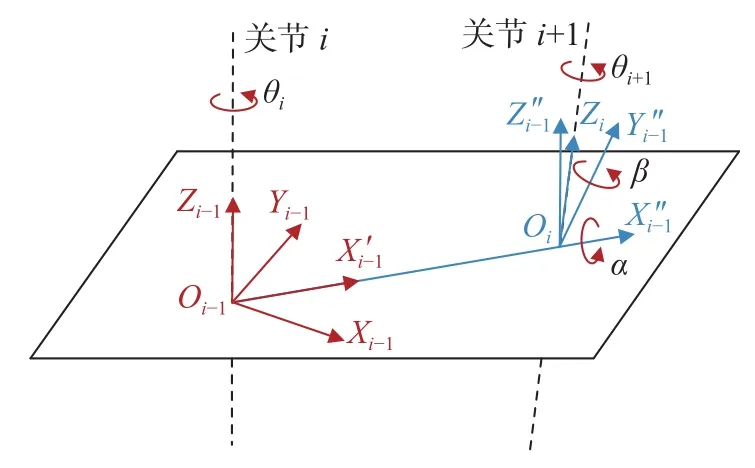
图2 基于M-DH的机器人平行关节转换关系

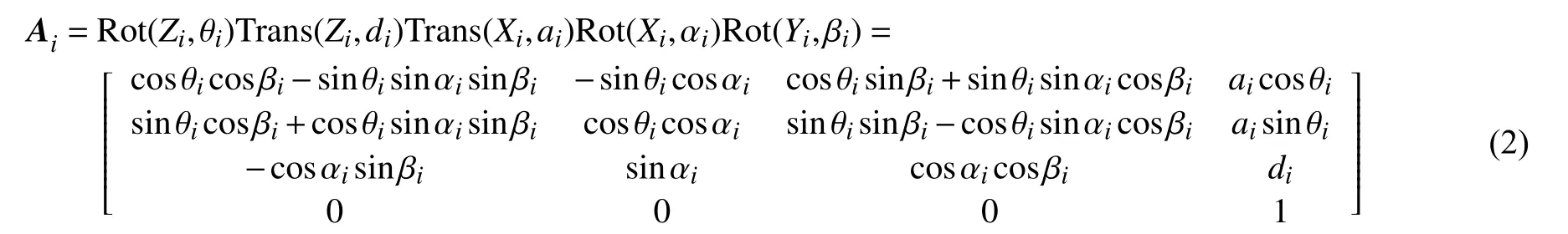
2.2 基于DE算法的运动学参数辨识

当位姿误差模型中的雅克比矩阵H存在线性相关的情况，会导致优化算法的辨识精度较差。为避免该问题，本文基于QR分解的方法分析M-DH位姿误差模型的冗余参数。根据QR分解的结果可知，运动学参数 β1，d2，β3，β4，β5，β6不需要辨识，因此待辨识参数的个数为24。

差分进化算法(differential evolution, DE)是由Storn R.和Price K. 于1995年提出一种基于群体差异的启发式随机搜索算法，该算法主要用于求解实数优化问题，具有容易实现、收敛快速、鲁棒性强等特点。DE算法主要分为初始化、变异、交叉和选择四项基本操作。在参数辨识的过程中将长度参数ai、di的误差上下限定义为0.05 mm，而角度参数αi、θi的误差上下限定义为0.01 rad。DE算法优化的目标函数如式(6)所示。f是运动学参数误差(Δai，Δdi，Δαi，Δθi，Δβi)的函数，经 DE 优化算法搜索机器人运动学参数误差值，使得适应度函数f最小，具体的运动学参数辨识流程图如图3所示。

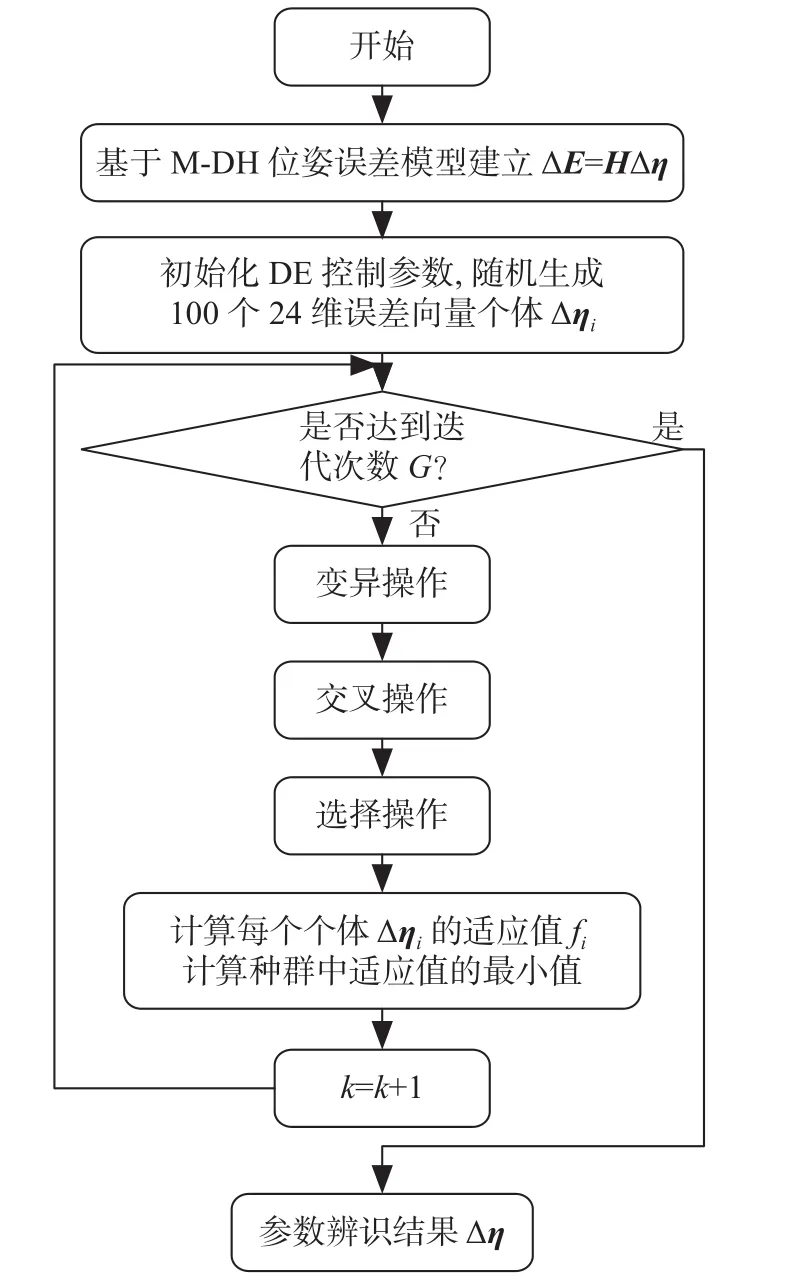
图3 DE优化算法的流程图

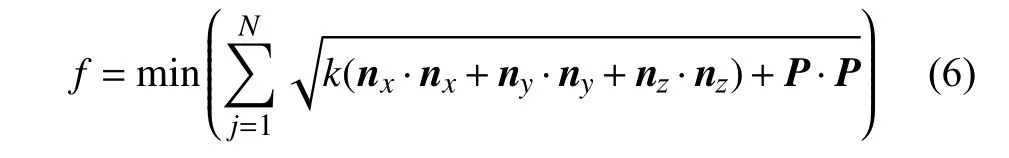
其中N为标定点数目，本文中取N=50；由于位置误差和姿态误差向量的量纲不同，本文利用调节因子k平衡位置误差向量和姿态误差向量在目标函数中的权重，本文中取k=30。

经过DE算法优化获得的M-DH参数误差值如表2所示，本文为衡量运动学参数误差的辨识效果，定义平均综合位置误差(average comprehensive position error，ACPE)和平均综合姿态误差(average comprehensive attitude error，ACAE)的计算如下：

表2 Staubli TX60机器人M-DH运动学模型参数的误差

式中：M——数据集中定位点的数目；

Δx，Δy，Δz——x，y，z轴向上的位置误差；

Δδ，Δφ，Δγ——x，y，z轴向上的角度误差。

辨识前后的机器人位置误差和姿态误差分别如图4和图5所示。辨识集的50个测量点的平均综合位置/姿态误差分别从(0.559 2 mm，0.152 2°)降低为(0.118 8 mm，0.077 2°)。为验证辨识后的M-DH模型精度效果，本文计算验证集的950个测量点的平均综合位置/姿态误差分别从(0.536 8 mm，0.174 5°)降低为 (0.177 2 mm，0.087 5°)。从以上结果可以看出经过基于位姿误差模型标定后的TX60机器人的精度性能得到了较大程度的提升。辨识数据集和验证数据集的位置误差和姿态误差相差不大，说明辨识得到的运动学模型具有较好地泛化能力。但基于位姿误差模型的机器人标定效果受限于标定点的空间分布，机器人的精度性能在未进行标定点测量的运动空间内相对较差，因此，具有较强的区域性。

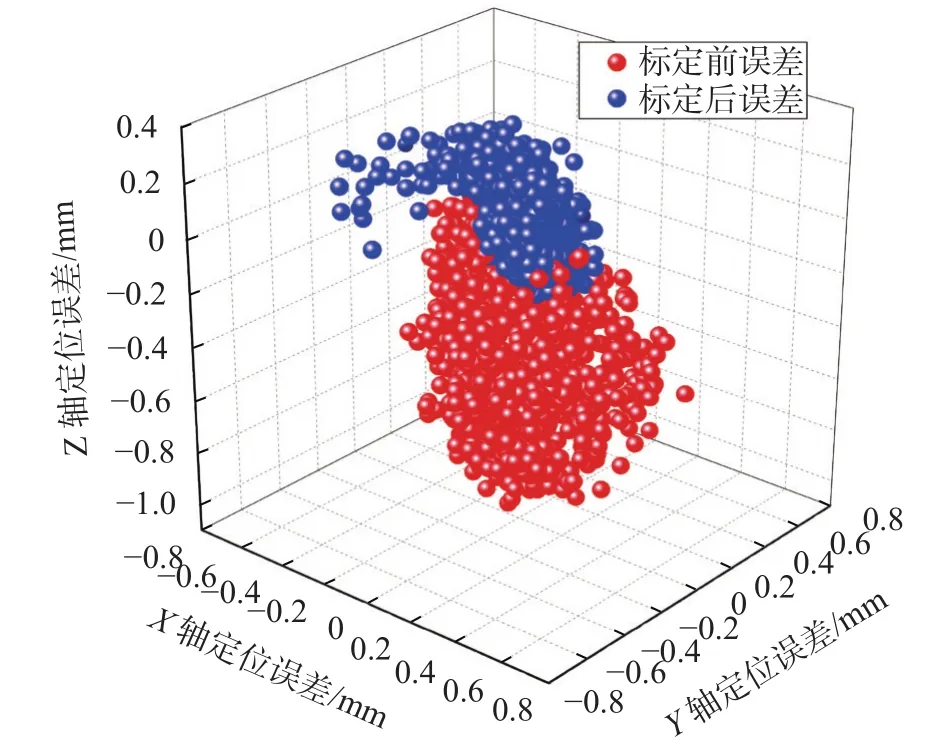
图4 标定前后的机器人平均综合位置误差

图5 标定前后的机器人平均综合姿态误差

3 基于RBF神经网络的工业机器人剩余误差拟合预测

经过以上运动学参数误差补偿后，机器人仍存在一定位置和姿态误差。文献[22]中表明，工业机器人的绝对定位误差可以达到重复定位误差水平。为进一步提升工业机器人精度性能，本文利用径向基函数（RBF）神经网络对剩余误差进行拟合预测。

RBF神经网络是一种局部逼近的神经网络，该网络能够以任意精度逼近任何连续函数。其网络结构与多层前向网络类似，是一种三层前向网络，如图6所示。该神经网络的第一层为输入层，该层的输入信号为机器人的关节向量 θ=[θ1, θ2, θ3, θ4, θ5,θ6]；第二层为隐含层，该层采用高斯函数作为激活函数；第三层为输出层，该层的输出信号为机器人末端的位姿误差向量 [Δx, Δy, Δz, Δδ, Δφ, Δγ]，该误差向量为经过位姿误差模型标定后的剩余误差。

图6 径向基神经网络结构

本文将1 000个测量点分为两个数据集，其中训练数据集包含700个测量点，验证数据集包含300个测量点，RBF神经网络的训练目标精度设置为 0.000 1，经过 Matlab nntool工具箱训练后的RBF神经网络的隐含层神经元个数为550，该RBF神经网络对TX60机器人位姿误差的预测结果如图7和图8所示。从图中可以看出训练集中的测量点误差得到较大程度的降低，训练数据集的平均综合位置/姿态误差从 (0.159 8 mm，0.088 1°)降低为(0.040 3 mm，0.017°)。测试数据集的测量点误差并未像训练数据集一样得到相同程度地改善，测试数据集的平均综合位置/姿态误差从(0.217 8 mm，0.086 3°)降低为 (0.104 4 mm，0.041 1°)。但相比于单一的基于位姿误差模型标定法，本文提出的两级误差补偿方法的精度提升效果更优。

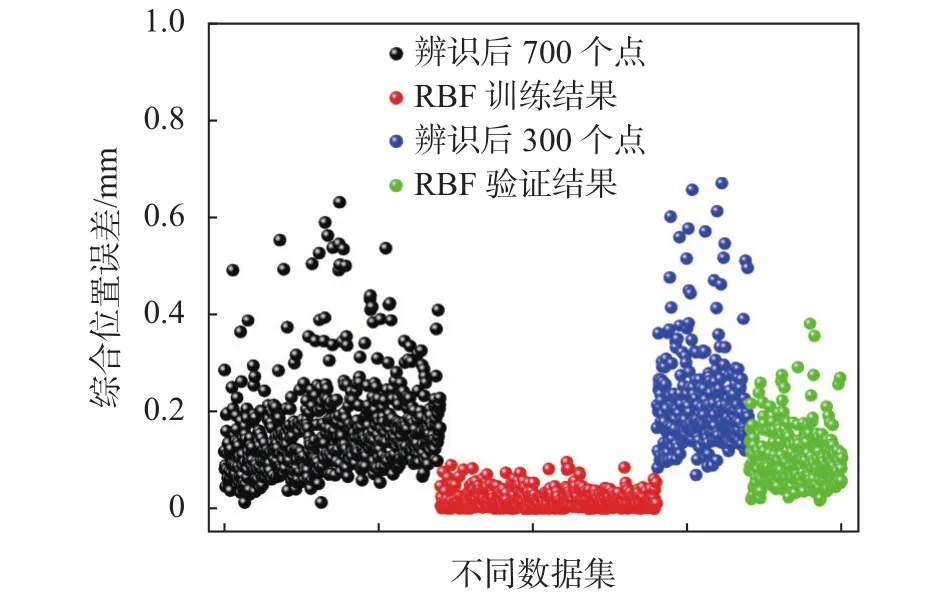
图7 基于径向基神经网络的工业机器人综合位置误差预测

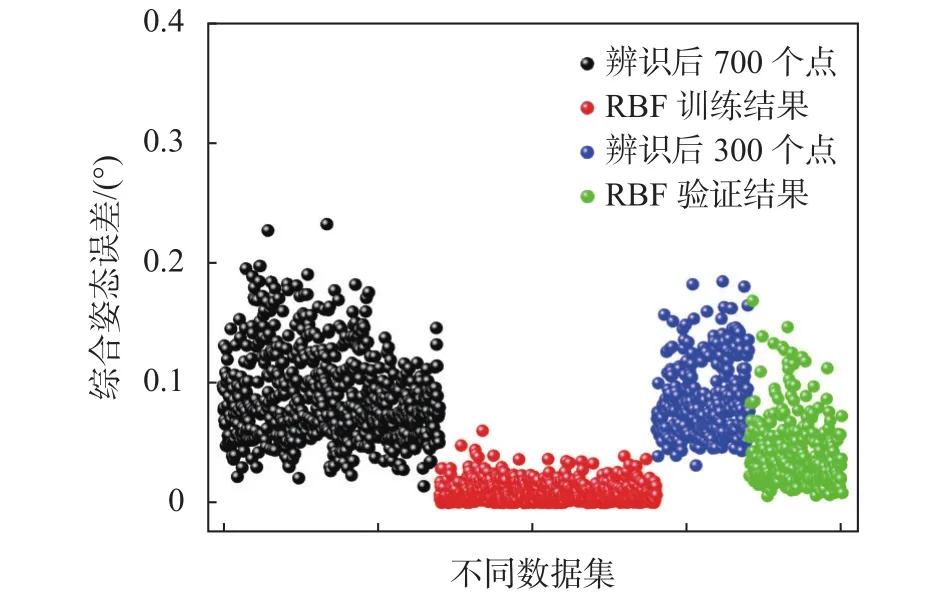
图8 基于径向基神经网络的工业机器人综合姿态误差预测

为进一步验证本文提出的两级误差标定方法的性能，本文将相同结构的RBF神经网络直接用于TX60机器人的位姿误差拟合，该RBF神经网络的隐含层神经元个数为550，其输出层的输出信号为机器人末端的位姿误差向量 [Δx, Δy, Δz, Δδ, Δφ,Δγ]，该位姿误差向量为测量得到的位姿误差向量，并未经过运动学参数误差补偿，所采用的训练数据集和验证数据集与之前采用的数据相同，两种方法的对比结果如图9所示。从图中可以看出，在采用相同的RBF神经网络结构时，基于两级标定方法的机器人精度性能提升效果要优于基于RBF神经网络的标定方法，其中验证数据集的平均综合位置误差相差0.005 4 mm，平均综合姿态误差相差0.007 2°，提升比例分别是4.9%和14.9%。

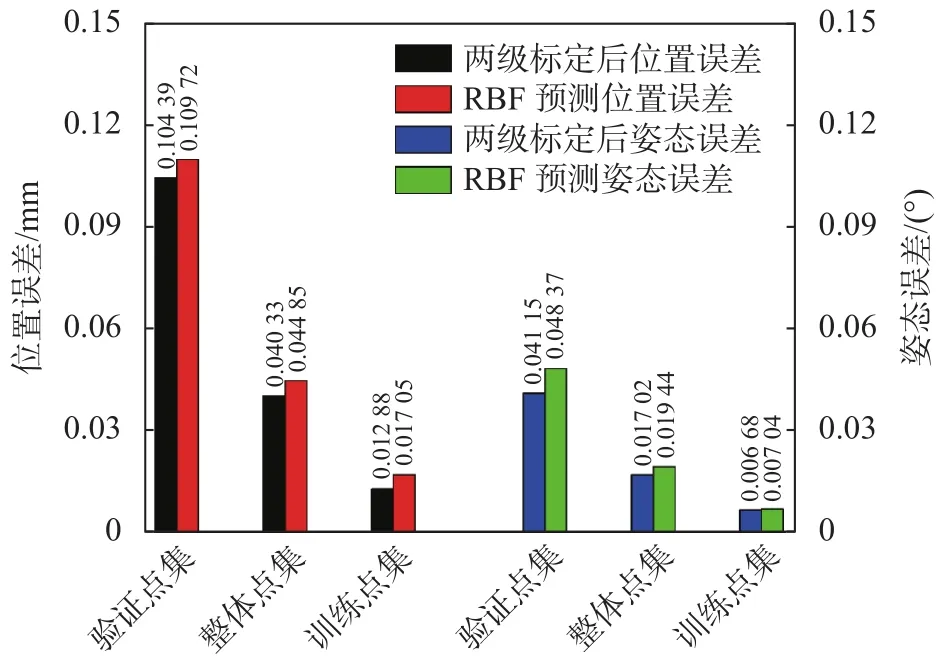
图9 基于径向基神经网络的工业机器人综合姿态误差预测

综上所述，本文提出的两级误差标定方法的机器人精度性能提升效果优于基于位姿误差模型标定方法和基于RBF神经网络标定方法。

4 结束语

针对串联型工业机器人的精度性能提升方法展开研究，本文提出了一种两级误差标定方法，该方法有机地融合了误差模型法和基于RBF神经网络的非模型标定方法。首先，基于M-DH运动学模型建立了串联型工业机器人的位姿误差模型，并基于DE优化算法实现了M-DH运动学参数误差的辨识，将TX60机器人的平均综合位置/姿态误差从(0.536 8 mm,0.174 5°)降低为 (0.177 2 mm, 0.087 5°)。其次，为了进一步提升机器人的精度性能，本文利用RBF神经网络拟合预测TX60机器人的剩余误差，该方法将机器人测试集的平均综合位置/姿态误差从(0.159 8 mm,0.088 1°)降低为 (0.040 3 mm, 0.017°)。将验证集的平均综合位置/姿态误差从(0.217 8 mm, 0.086 3°)降低为(0.104 4 mm, 0.041 1°)。从而证明了本文提出的两级误差标定方法能够有效地提升机器人的精度性能，并且精度优化效果优于单一的基于误差模型的误差标定方法。最后，为了进一步验证本文提出的误差标定方法的有效性，本文直接利用RBF神经网络拟合机器人的定位误差，结果表明，基于两级误差标定方法的精度提升效果要优于单一的基于RBF神经网络的误差标定方法。研究表明工业机器人的精度性能具有明显的区域性，本课题组后期将重点研究工业机器人全运动空间的精度提升方法，从而保证工业机器人的通用性。