基于活动发生关系重要系数的流程模型相似性度量
王倩倩, 邵叱风, 王 颖
(安徽科技学院 信息与网络工程学院,安徽 凤阳 233100)
对于一个组织或者企业来说,业务流程是其重要组成成分。现今社会,业务流程为适应时代的变化,满足各种需求,也在不断变化。如果每次变化都从头开始进行构建业务流程是非常耗时间的。为了重建业务流程,一般采用流程聚类、流程查询等先进技术,这些技术的前提是计算流程相似性。
对于相似性的计算方法,有不少学者做了相关的研究。文献[1]通过计算2个流程之间的距离来度量流程模型相似性,这种距离度量可以用作过程挖掘、流程合并和流程聚类中的定量和定性工具,最终它可以减少或最小化工作流系统的设计、分析和演化所涉及的成本。但是只能定量的测量,没有考虑变量约束。文献[2]考虑可变时间约束,提出时间依赖图(TDG)的概念,通过计算两个TDG的距离来表示流程之间的相似性。但此计算方法的前提是节点标签相同,而现实情况是节点标签不一定相同。文献[3]提出一种基于节点标签的相似性度量。虽然它的计算速度很快,但忽略流程的行为特征会导致结果不准确。文献[4]提出了一种基于变迁邻接关系集(TAR)的业务流程之间的相似性度量,该度量忽略了变迁邻接关系的重要性,使得顺序关系与循环结构不易区分。之后,文献[5]添加了变迁邻接关系的重要性,提出了基于变迁邻接关系重要性的相似性算法TAR++,可有效区分顺序关系与循环结构。文献[6]对邻接关系进行扩展提出行为轮廓(BP)概念,用BP计算流程一致性,并与迹等价的概念下的一致性对比,凸显出行为轮廓计算相似性的优越性。文献[7]阐述了一种在不同视角下的应急处置流程相似性计算方法。该方法是在应急处置活动流程化的基础上,将各部门之间的联动模式分为以下几种类别:活动同步、活动选择、讯息传播,并建立四个试图,进而以四个视图为基础,给出了不同视图表示下应急处置流程的相似度计算方法。文献[8]概述了有关业务流程模型相似性度量的最新技术,旨在分析存在哪些相似性度量、它们如何表征以及通常应用哪种计算来确定相似性值。最后,通过对 123 个相似性度量的分析,提出对相似性度量进行比较分析,研究人类输入与相似性度量的整合以及作为未来研究机会进一步分析相似性度量使用场景需求的建议。文献[9]提出基于LBP的相似性度量算法,但是一旦缺少日志,算法则不可行。
综合上面的分析,在文献[6]的启发下,提出一种基于活动发生关系重要系数的流程模型相似性度量方法。首先给出活动间的3种发生关系,并考虑其重要系数,给出重要系数的计算方法,然后基于活动发生关系及其重要系数给出了计算流程模型行为相似性的方法,最后验证方法的有效性。
1 预备知识
定义1[4](Petri网)Petri网是一个元组(P,T,F)
1)P是有限库所集;
2)T是有限变迁集,P∪T≠ø,P∩T=ø;
3)F⊆(P×T)∪(T×P)为流关系,将P和T连接。
定义2[4](工作流网)Petri网WN=(P,T,F)是一个工作流网,当且仅当:
1)PN具有一个源库所i:·i=φ;
2)PN具有一个汇库所o:o·=φ;
3)如果添加一个变迁t*到PN,连接库所i和o,即·t*={i},(t*)·={o},导致Petri网是强连接的。
定义3(活动发生关系)WN=(P,T,F)是一个工作流网,Σ为所有可能发生序列的集合,t1和t2为活动,且t1,t2∈T
1)因果关系:若t1发生可使t2发生,则t1和t2之间存在因果关系,记作t1→t2或t2←t1(即逆序关系),如图1a;
2)并行关系:若t1发生可使t2发生,同时t2的发生可使t1发生,则称t1和t2之间存在并行关系,记作t1‖t2或t2‖t1,如图1b;
3)互斥关系:t1和t2不能同时发生,则称t1和t2之间存在互斥关系,记作t1#t2或t2#t1,如图1c。
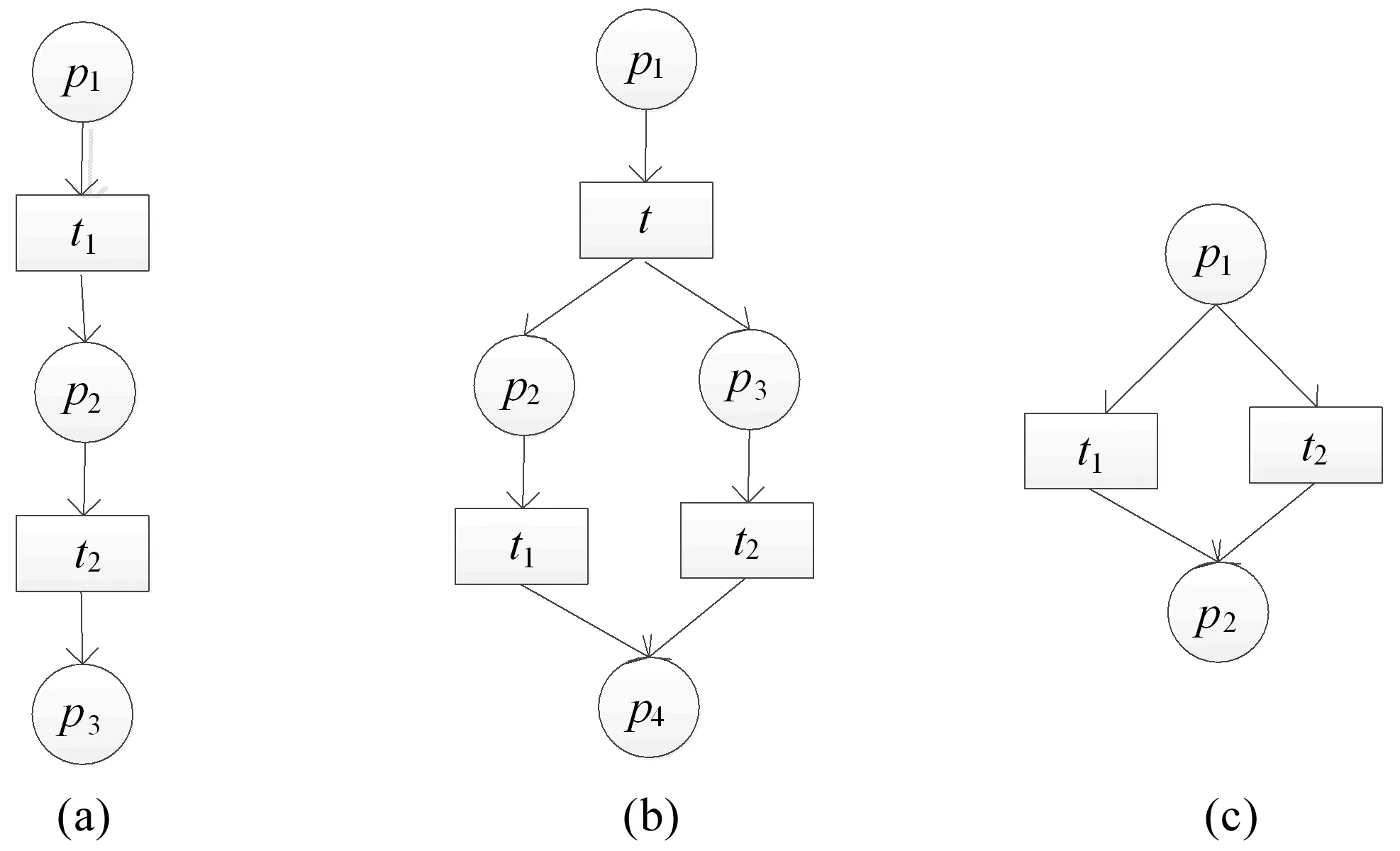
图1 活动发生关系图
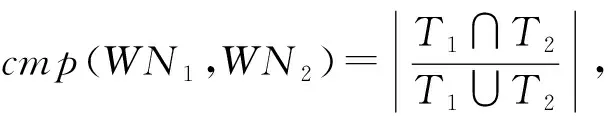
比较两个工作流网之间的相似性的前提是它们是σ-兼容的。如果它们不σ-兼容,那么认为它们不相似,不需要继续比较它们。
在图2中,给出了3个工作流网g0,g1和g2,来说明如何比较工作流网间的兼容性。

图2 兼容性示例
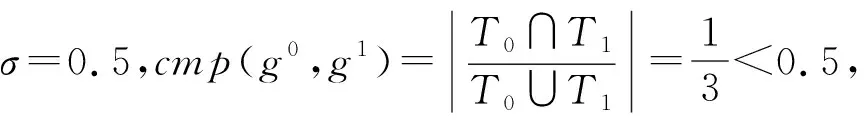
定义5(活动关系矩阵)令WN=(P,T,F)为一个工作流网,WN的活动关系矩阵M定义如下:
定义6(活动关系重要系数)给定两个工作流网WN1=(P1,T1,F1),WN2=(P2,T2,F2),则因果关系重要系数、并行关系重要系数、互斥关系重要系数分别为I1,I2,I3
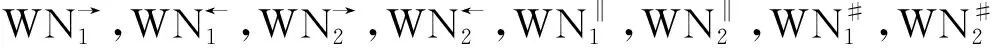
定义7(活动关系相似性)令WN1=(P1,T1,F1),WN2=(P2,T2,F2)为两个工作流网,因果关系、并行关系,互斥关系的相似性分别为sim→(WN1,WN2),sim‖(WN1,WN2),sim#(WN1,WN2)
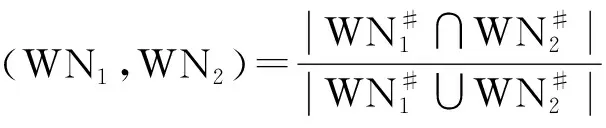
定义8(WN相似性)令WN1=(P1,T1,F1),WN2=(P2,T2,F2)为两个工作流网,因果关系、并行关系,互斥关系的相似性分别为sim→(WN1,WN2),sim‖(WN1,WN2),sim#(WN1,WN2),则WN1与WN2的相似性为
sim(WN1,WN2)=I1×sim→(WN1,WN2)+I2×sim‖(WN1,WN2)+I3×sim#(WN1,WN2)
2 工作流间的相似性计算
本文提出的基于活动发生关系重要系数的流程模型相似性度量方法即算法1工作流间的相似性计算,首先分析两个工作流网之间是否兼容,兼容则可计算相似性,然后计算因果关系、并行关系、互斥关系的相似性,最后计算完整的两个工作流网的相似性。
算法1工作流间的相似性计算
输入:工作流网WN1与WN2
输出:WN1与WN2的相似性
Step1:输入两个工作流网WN1与WN2;
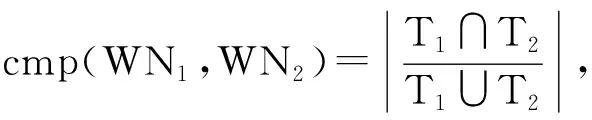
Step3:遍历WN1与WN2的所有活动,根据活动发生关系的定义,确定所有活动相互之间的关系,即t1→t2或t2←t1或t1‖t2或t2‖t1或t1#t2或t2#t1;
Step4:根据定义5列出WN1与WN2的活动关系矩阵M1,M2;
Step5:计算WN1与WN2的所有活动关系的重要系数I1,I2,I3
Step6:利用定义7计算WN1与WN2中因果关系、并行关系、互斥关系的相似性sim→(WN1,WN2),sim‖(WN1,WN2),sim#(WN1,WN2),
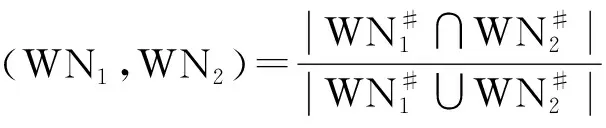
Step7:根据定义8计算WN1与WN2的相似性
sim(WN1,WN2)=I1×sim→(WN1,WN2)+I2×sim‖(WN1,WN2)+I3×sim#(WN1,WN2)
Step8:算法结束。
3 实例分析
本文引用文献[10]的两个工作流网来验证算法的可行性,即通过算法1来计算两个工作流网的相似性,工作流网如图3。
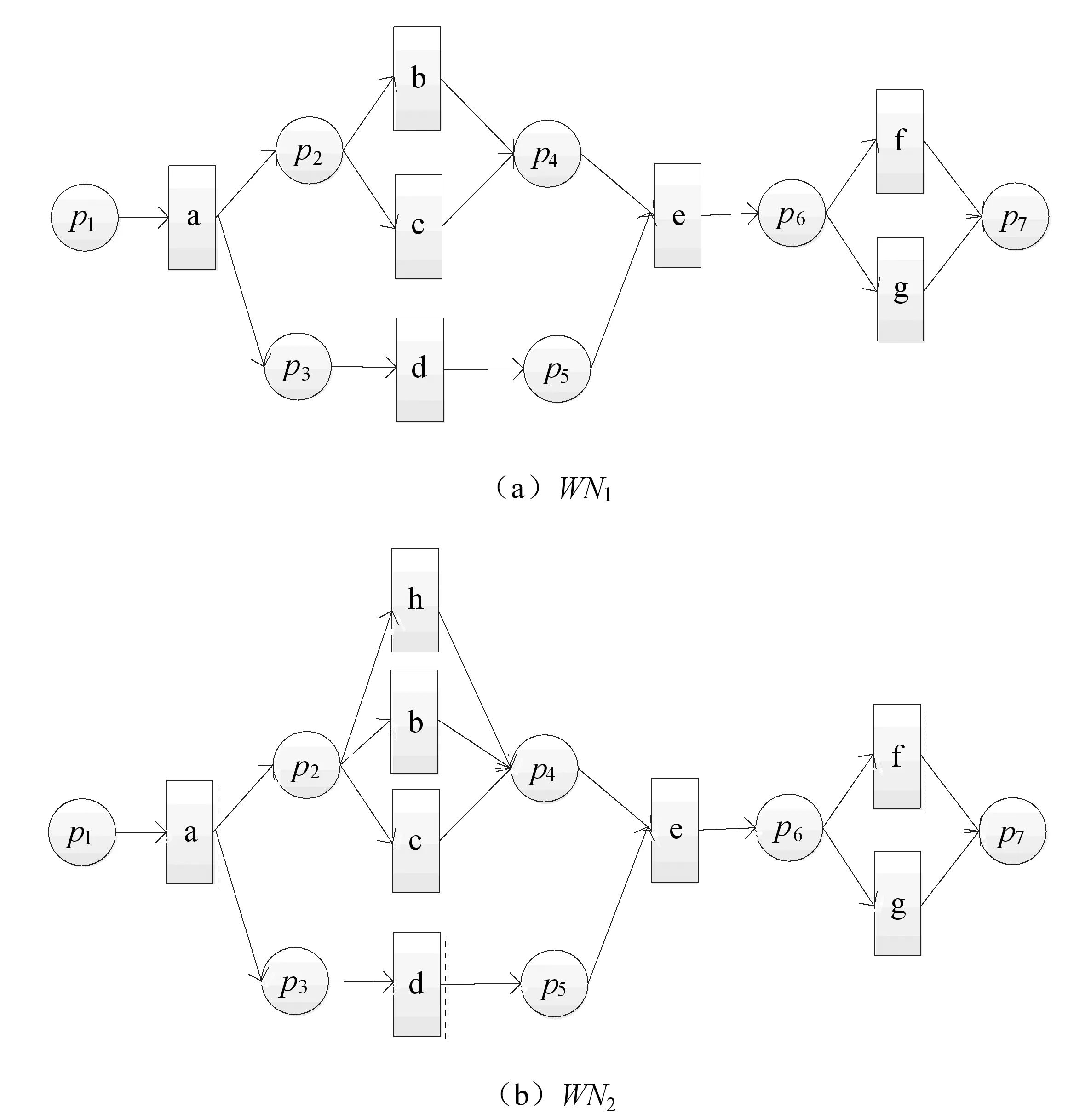
图3 工作流网WN1和WN2
运行Step3~4,输出WN1与WN2的活动关系矩阵M1,M2:
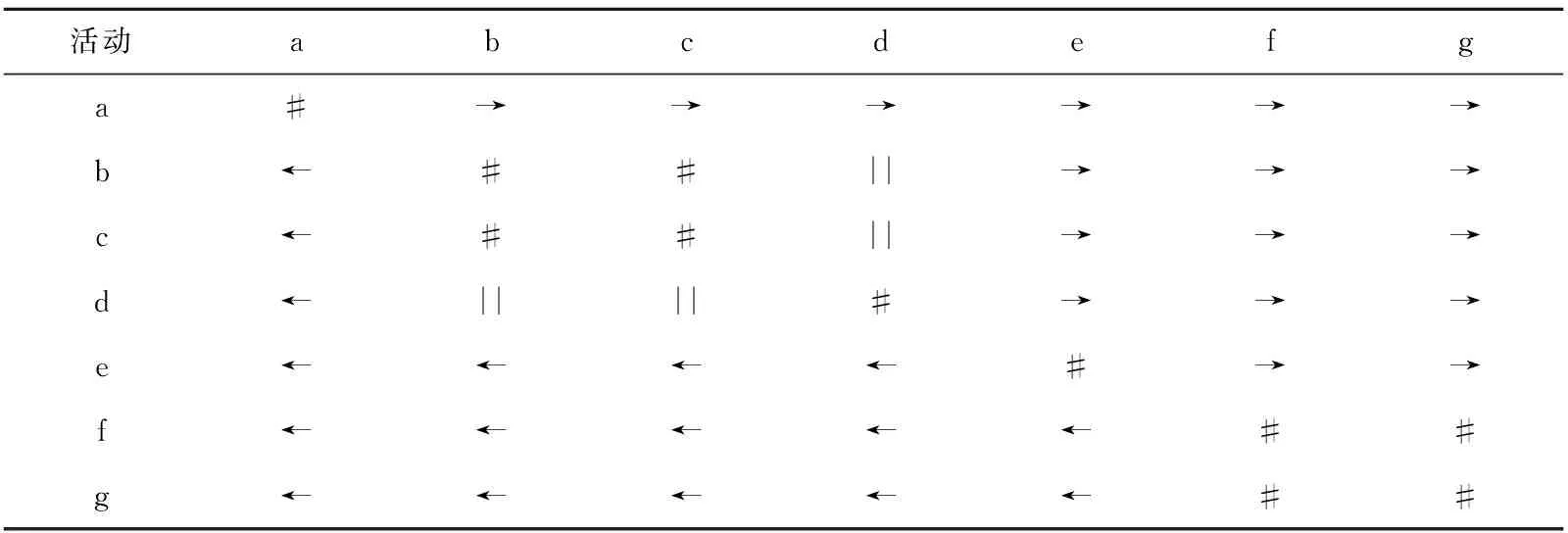
表1 活动关系矩阵M1
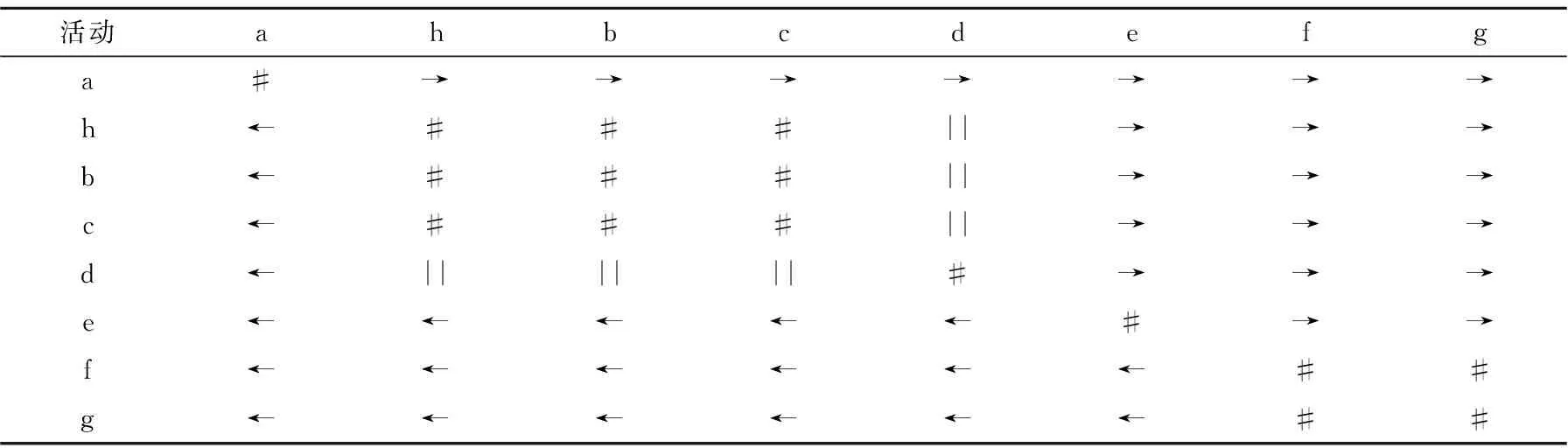
表2 活动关系矩阵M2
运行Step5,计算活动关系的重要系数I1,I2,I3,由表2~3可知,
(d,d),(e,e),(f,f),(f,g),(g,g),(g,f)}
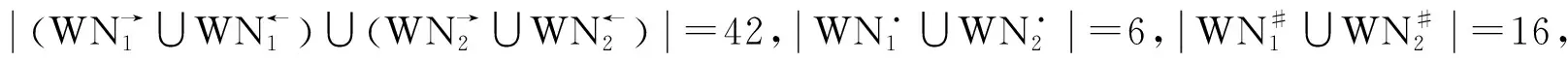
运行Step6,计算每个活动关系的相似性:
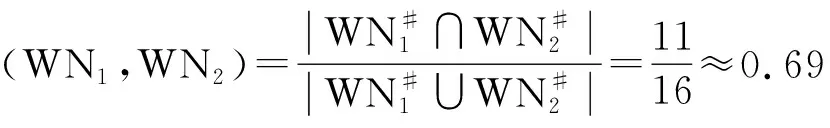
运行Step7,计算WN1与WN2的相似性:
sim(WN1,WN2)=I1×sim→(WN1,WN2)+I2×sim‖(WN1,WN2)+I3×sim#(WN1,WN2)=0.66×0.81+0.09×0.67+0.25×0.69≈0.77
根据算法1计算WN1与WN2的相似性为0.77。表3展示了用其他算法计算WN1与WN2的相似性。

表3 算法结果比较
由表3结果对比可知,算法1与其他算法结果接近,说明算法1的可行性。
4 结论与讨论
计算流程之间的相似性是在涉及业务流程管理的广泛应用中执行的任务。相似性度量可在简化更改、合并流程、促进重用、流程检索等方面应用。为了简化管理并促进流程变量的重用,提出了基于活动发生关系重要系数的流程模型相似性度量方法。首先判断两个工作流网的兼容性,其次计算两个工作流的活动关系矩阵,并计算两个工作流网的3种活动关系的相似性,然后将重要系数分配给对应的活动关系相似性,最后计算完整的两个工作流的相似性。算法对比结果也说明此算法的可行性。未来的工作将解决实际流程之间的相似性度量的其他开放问题,例如具有不同标签字母的过程和以及基于距离度量的过程模型聚类等。