基于深度神经网络EikoNet 走时计算方法及应用

姚 时，侯 爵3,，黄跃鹏，徐 涛，白志明，高正辉

1 中国科学院地质与地球物理研究所 岩石圈演化国家重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 中国地震局地球物理研究所，北京 100081

4 中国科学院地球科学研究院，北京100029

5 吉林大学地球探测科学与技术学院，长春 130026

0 引 言

地震波走时计算在层析成像（徐涛等, 2014,2015; Liang et al., 2016; 张明辉等, 2019; 林吉焱等,2020）、偏移成像（Gray and May, 1994; Sun, 1998;刘国峰等, 2009）和微震定位（Ben-Zion et al.,2015; Inbal et al., 2015）中都发挥着重要的作用. 目前走时计算的方法可分为射线追踪类（Julian and Gubbins, 1977; 徐涛等, 2004; Xu et al., 2006; Rawlinson et al., 2008; 李飞等, 2013）和程函方程数值求解类（Vidale, 1988, 1990; Sethian, 1996, 1999; Rawlinson and Sambridge, 2004; Zhao, 2005; Qian, 2007a,2007b; Treister and Haber, 2016）. 射线追踪类方法需要先计算射线路径，然后沿着射线路径计算走时，在检波点较多的情况下计算效率较低，且在模型复杂时会出现阴影区等问题（Xu et al., 2010, 2014）.程函方程数值求解类方法有效避免了上述问题，此类方法中最常用的是快速推进法（fast marching method, FMM）和快速扫描法（fast sweeping method, FSM）. FMM （Sethian, 1996, 1999; Rawlinson and Sambridge, 2004; Treister and Haber, 2016）是一种基于网格的差分数值计算格式，主要包括利用迎风差分格式求解局部程函方程获取走时和利用窄带技术模拟波前的传播过程两个步骤. FSM（Zhao, 2005; Qian et al., 2007a, 2007b）是一种利用Gauss-Seidel 或者Gauss-Jacobi 迭代格式进行迎风差分求解程函方程的迭代方法，首先基于因果关系将走时场传播的方向分成有限数量的组，对于每一组分别利用选定的迭代方法求解非线性逆风差分格式离散化后的方程组. FMM 和FSM 对速度变化很大的非均匀介质依然有很好的稳定性和适用性，均可以准确地计算地震波走时（兰海强等，2012）. FMM 和FSM 都属于有限差分类方法，在计算走时的过程中需要求解由每一个震源激发的走时场，而走时的计算是一个消耗时间和存储空间的过程，因此，计算走时的时间和内存消耗都会随着震源和网格数量的增加而增加.

深度学习是一种以神经网络为架构、对数据进行表征学习的算法（Hinton et al., 2006; Goodfellow et al., 2016），目前，深度学习方法在许多地震学问题中已经开始发挥较大的作用（杨旭等，2021），包括以速度模型为输入预测介质的声波响应（Moseley et al., 2018）、提高黏弹性模拟的速度（DeVries et al., 2017）、使用无监督神经网络解决偏微分方程的正反演问题（Bar and Sochen, 2019）、利用卷积神经网络进行地震波走时层析成像（Fan and Ying, 2019）、地震波形反演（Sun et al.,2020）、利用卷积神经网络进行地震波形自动分类与识别（赵明等，2019）和地震数据随机噪声去除（韩卫雪等，2018）等. 此外，还可以向网络中加入数学物理定律等先验知识构建基于物理信息高效的神经网络，以解决更复杂的物理问题（Raissi et al., 2019）. Smith 等（2020）提出了一种名为EikoNet的使用深度神经网络求解程函方程的方法. EikoNet方法在给定速度模型和其中任意两点的情况下可以无网格地快速确定两点之间的走时. 该方法通过在三维空间中采样生成训练样本，以给定的速度模型为标签实现训练过程中对网络的优化. 并且，在训练过程中，空间梯度都是利用神经网络的可微性解析计算的. 此外，EikoNet 可以大规模并行、训练和预测都可以在GPU 上进行，这样就使得其计算效率显著提高，并同时大大降低其在内存上的消耗.

本文使用EikoNet 方法和FMM 在均匀速度模型、块状速度模型、层状速度模型和棋盘格速度模型上进行了实验，对比了二者的效率和精度.

1 方法原理

1.1 EikoNet

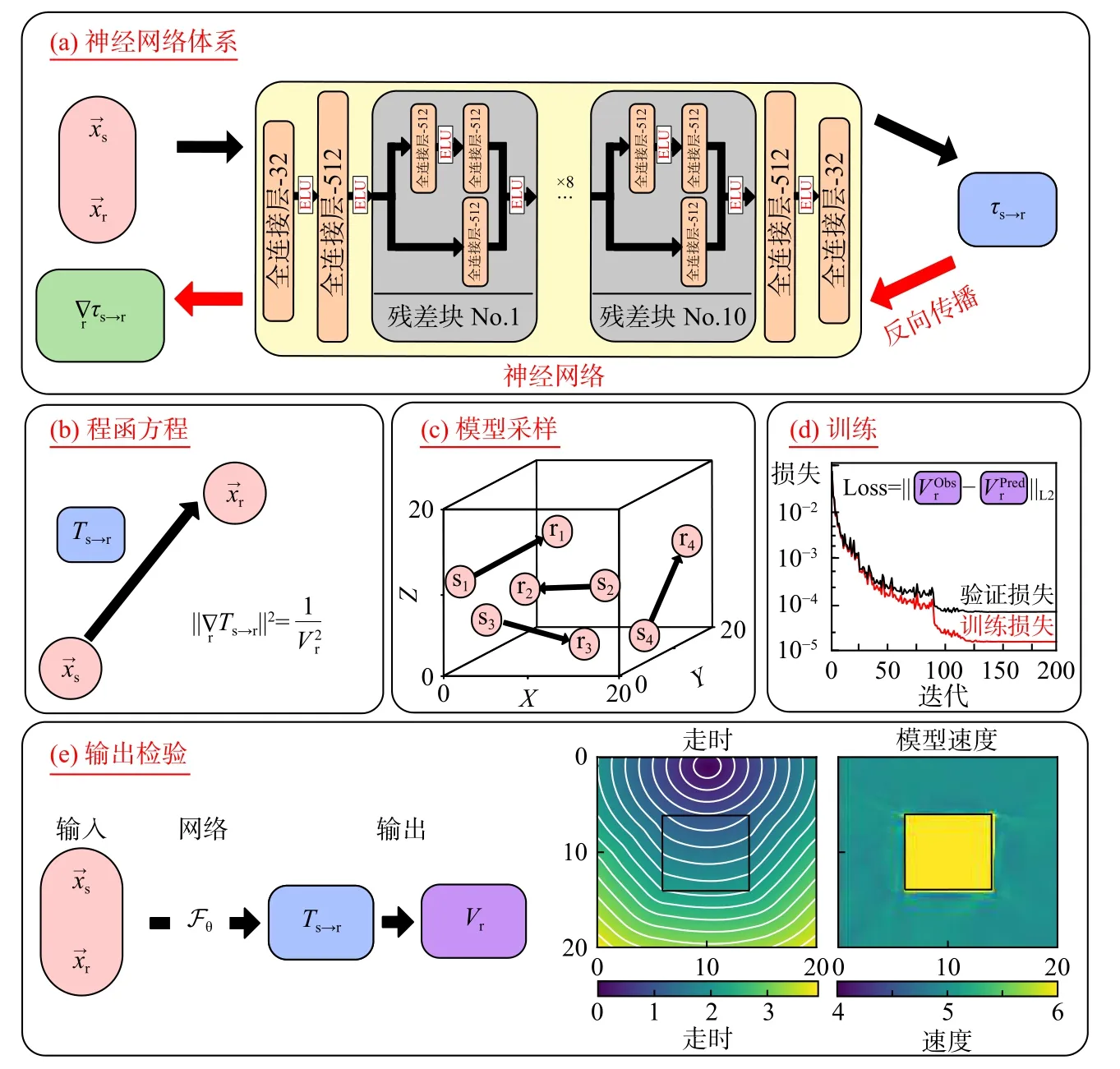
图 1 处理工作流概述.（a）由全连接层和残差块组成的神经网络体系结构，每个残差块由3 个全连接层组成，有512 个神经元，ELU 激活应用于所有隐藏层.（b）T s→r 和 Vr的程函方程总结.（c）在整个三维空间采样源-接收对构建训练数据集.（d）通过最小化与预测和已知速度值相关的损失函数进行网络训练.（e）通过传递用户定义的源-接收对检查神经网络输出（修改自Smith et al., 2020）Fig. 1 Overview of the processing workflow. (a) Neural network architecture composed of fully connected layers and residual blocks. Each residual block is composed of three fully connected layers with 512 neurons. ELU activations are applied on all hidden layers. (b) Summary of Eikonal equation for Ts→r and Vr. (c) Sampling of source-receiver pairs across the 3-D volume to build the training data set. (d) Network training through the minimization of loss function relating predicted and observed velocity values. (e) Inspection of neural network outputs by passing user-defined source-receiver pairs (modified from Smith et al., 2020)

如图1 所示，EikoNet 是一个多层的前馈神经网络，由一系列全连接层组成的残差块和其后的非线性单元构成，使用pytorch 深度学习框架搭建，不同的残差块可以使用跳层连接的方式实现，缓解了在深度神经网络中增加深度带来的梯度消失问题，并解决了深度神经网络的退化问题，并且可以通过增加一定的深度来提高神经网络计算的准确率.

EikoNet 的输入是6 维的数据，输出是一维的数据，其输入和输出结构各由两个线性层组成，维数变化分别为 6 →32 →512和 512 →32 →1. 其实现大致可分为以下四个步骤：

（1）模型采样

使用加权随机采样的方法从连续的三维介质中随机采样源点和接收点，权值通过网络预测的速度和真实速度的相对误差来定义，并将每个点的速度标注在接收点的位置来建立训练数据集.

采取的样本形式为 (

x

,

y

)

，

x

是源点和接收点坐标的集合，

y

为接收点处的速度.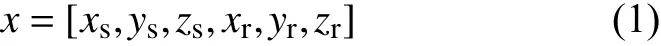

式中，

x

,

y

,

z

表示源点和接收点的坐标，下标s 和r分别代表源点和接收点.

（2）正向传播

源点和接收点之间经分解的走时可以表示为:

式中，

T

=‖→

x

-→

x

‖，表示接收点到源点之间的距离函数； τ是实际走时和

v

=1的均匀速度模型走时的偏差.

程函方程是一个非线性的一阶偏微分方程，其一般形式为：

式中，

s

和

v

分别代表慢度和速度.

将式（3）代入（4）并展开可以得到因式程函方程：

训练一个深度神经网络

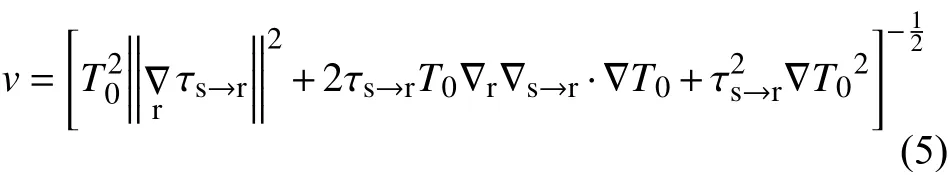
f

来预测输入源点和接收点之间的走时偏差. 走时偏差可以表示为：

开始训练之前 τ是未知的，我们可以赋予 τ一个初始值，利用式（5）可以计算得到速度，将此速度定义为预测速度

v

ˆ，此过程中涉及到的空间梯度都可以利用神经网络的可微性进行计算.

（3）反向传播

利用

v

ˆ 和 已知的速度

v

可以定义一个均方误差损失函数：

将计算得到的失配函数反向传播梯度到神经网络的参数，通过迭代更新每个神经元的参数来最小化目标函数，在此过程中就达到了优化网络的作用.

（4）结果输出

针对每一个速度模型都需要进行一次神经网络的训练，在本文中设置网络训练的迭代次数为200，每次训练大约需要2～3 个小时. 神经网络训练完成后，只需要保存90 M 左右的神经网络模型，在三维速度模型中给定一定数量的源点和接收点就可以快速输出预测的走时场.

1.2 快速推进法（FMM）

本文使用快速推进法（FMM）计算走时，主要用于与EikoNet 方法的计算结果进行对比，FMM 方法求解的是一般形式的程函方程式（4）.首先，我们可以使用迎风差分格式近似程函方程的时间梯度项，基于网格的数值格式求解局部程函方程获取走时.

随后，使用窄带技术模拟波前的传播过程，如图2a 所示，窄带技术将计算区域内所有网格节点分为走时计算已完成的完成点（黑色）、已计算走时但还未确定最小值的窄带点（灰色）和未进行走时计算的远离点（白色）. 图2b 展示了窄带技术从源点向外拓展的几个步骤，重复此过程可以计算得到所有网格点的走时.

1.3 快速扫描法（FSM）

本文使用精细网格因式分解的FSM（周小乐等，2020）计算走时，主要用作参考解对比EikoNet方法和FMM 方法的精度.

图 2 （a）窄带技术原理示意图. （b）从源点开始的窄带拓展示例（修改自Rawlinson and Sambridge, 2004）Fig. 2 (a) The principle of the narrow-band method. (b) Example of how the narrow band evolves from a source point(modified from Rawlinson and Sambridge, 2004)

快速扫描法主要有两个步骤，首先，给所有的网格点赋初始走时值，后续计算时会被更新；在交替的4个方向上，使用Gauss-Seidel 型迭代法求解离散的非线性方程组，分别按4 个方向扫描.

2 数值模型实验

2.1 精度效率对比方法

2.1.1 精度对比方法

本文在不同模型下分别设置了走时解析解和精细网格下计算的走时数值解作为走时参考解，通过计算EikoNet 方法和FMM 与走时参考解的相对误差来衡量精度.

（1）均匀速度模型的走时参考解

在均匀速度模型中，我们使用程函方程的解析解作为走时参考解.

（2）其他速度模型的走时参考解

对于块状速度模型、层状速度模型和棋盘格速度模型，则使用1.3 节中提到的因式分解的FSM来计算程函方程走时作为走时参考解.

我们采用以下步骤确定其走时参考解：

①给定一个初始的网格间距，使用上述方法计算走时场并保存走时计算结果；

②不断缩小网格间距，在每一个网格间距下分别计算一次走时场，将每一次的走时计算结果与上一次的走时计算结果进行对比计算误差；

③如果误差不再发生较大变化，我们就将此网格间距下的走时计算结果当作走时参考解，否则，重复步骤②.

最终，我们选择了0.05 km 的网格间距下得到的走时计算结果作为走时参考解.

（3）走时场相对误差

设走时参考解为

t

，使用EikoNet 计算得到的走时为

t

，使用FMM 计算得到的走时为

t

，EikoNet的计算误差为

P

，FMM 的计算误差为

P

，

P

和

P

的表达式分别定义为：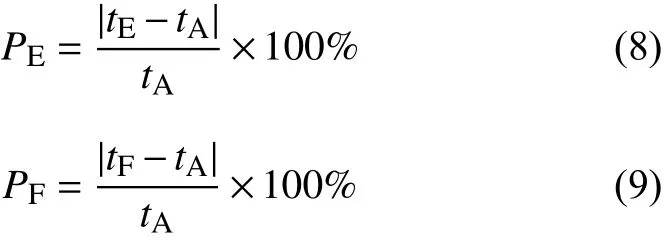

2.1.2 效率对比方法

在进行走时场计算的过程中，分别记录EikoNet方法和FMM 的计算耗时来衡量两种方法的效率.EikoNet 方法的走时计算是在Nvidia GeForce RTX 2080 Ti 上进行的，FMM 的走时计算是在Intel Core i9-9900K 上进行的.

2.2 计算实例

本文设置了四种速度模型，均为

X

×

Y

×

Z

=20 km×20 km×20 km 的三维模型，设置了两种震源位置以验证EikoNet 方法在不同的震源位置均具有较高计算精度，均匀速度模型、块状速度模型和层状速度模型分别对应于均匀介质、速度异常体和层状介质三种实际地质情况，棋盘格速度模型则是用来检验EikoNet 方法在计算过程中适应正负速度异常的能力，此外，使用FMM 进行计算时将网格间距设置为0.1 km.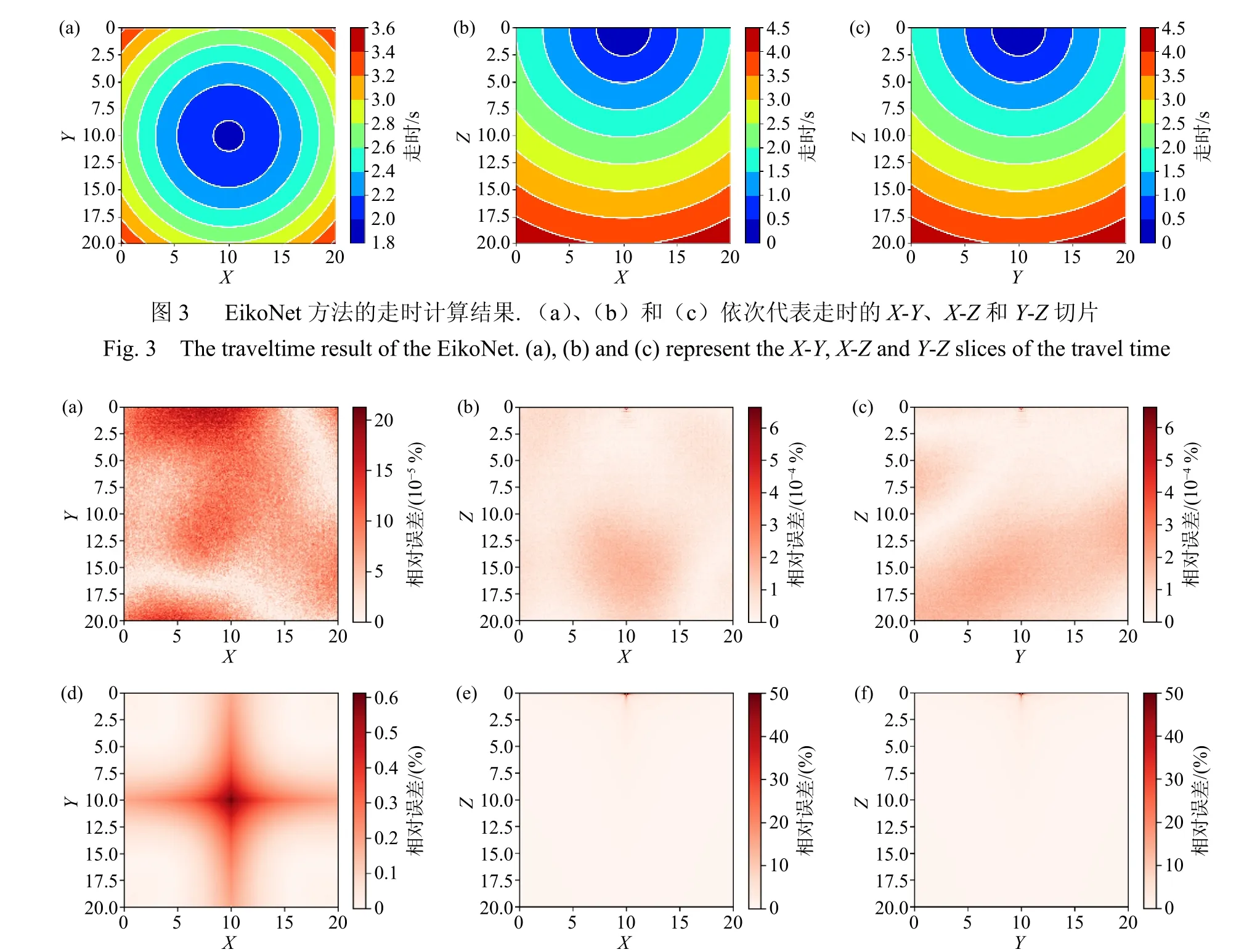

图 4 均匀速度模型走时计算相对误差. （a）、（b）、（c）和（d）、（e）、（f）依次EikoNet 走时计算相对误差和FMM 走时计算相对误差的X-Y、X-Z 和Y-Z 切片Fig. 4 The relative error of the traveltime calculation of the homogeneous model. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices of the relative error of the EikoNet and the relative error of the FMM

EikoNet 神经网络使用学习率为5×10的Adam优化算法，残差元数量为10，训练集样本数量为10，批尺寸为752，每个批次的数据尺寸为[752, 6]，每次学习迭代200 次，此外，针对每个速度模型都需要进行一次训练.

（1）均匀速度模型

设置模型的速度为5 km/s，震源放置在（10 km, 10 km, 0.1 km），EikoNet 方法的走时计算结果如图3 所示. 由图4 可以看出EikoNet 方法的走时计算相对误差基本为0，而FMM 则因为求解的是未经因式分解的程函方程，故而存在点源奇异性造成了误差值达到50%左右的近源误差，其相对误差平均值为0.34%. 此外，EikoNet 方法和FMM 的计算耗时分别为5.97 s 和27.53 s，效率比为4.61.

（2）块状速度模型

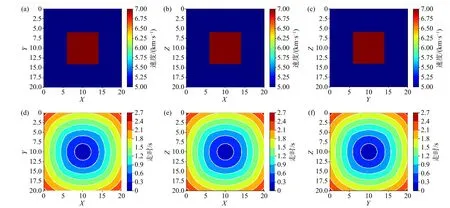
图 5 EikoNet 方法的走时计算结果. （a）、（b）、（c）和（d）、（e）、（f）依次代表速度模型和走时的X-Y、X-Z 和Y-Z 切片Fig. 5 The traveltime result of the EikoNet. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices of the velocity modeland the the travel time

图 6 块状速度模型走时计算相对误差. （a）、（b）、（c）和（d）、（e）、（f）依次代表EikoNet 走时计算相对误差和FMM 走时计算相对误差的X-Y、X-Z 和Y-Z 切片Fig. 6 The relative error of the traveltime calculation of the block model. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices of the relative error of the EikoNet and the relative error of the FMM

设置模型的背景速度为5 km/s，在模型的正中心增加了一个大小为8 km×8 km×8 km、速度为7 km/s的块体，震源放置在（10 km, 10 km, 10 km），EikoNet 方法的走时计算结果如图5 所示. 如图6 所示，EikoNet 方法出现了一些较小的误差，相对误差平均值为0.097%，而FMM 除近源误差外，在三维空间还存在着一些数值误差，相对误差平均值为0.74%. EikoNet 方法和FMM 的计算耗时分别为5.99 s 和28.51 s，效率比为4.76.

（3）层状速度模型

层状速度模型共有5 层，每层的深度均为4 km，1—5 层的速度依次为3 km/s、4 km/s、5 km/s、6 km/s和7 km/s，震源放置在（10 km, 10 km, 10 km），EikoNet 方法的走时计算结果见图7. 如图8 所示，EikoNet 方法在

Z

方向速度间断面上存在一定的误差，相对误差平均值为0.078%，FMM 除源点附近的误差外，在其他区域内也分布着一些比EikoNet方法更大的误差，相对误差平均值为0.84%. EikoNet方法和FMM 的计算耗时分别为6.09 s 和30.64 s，效率比为5.03.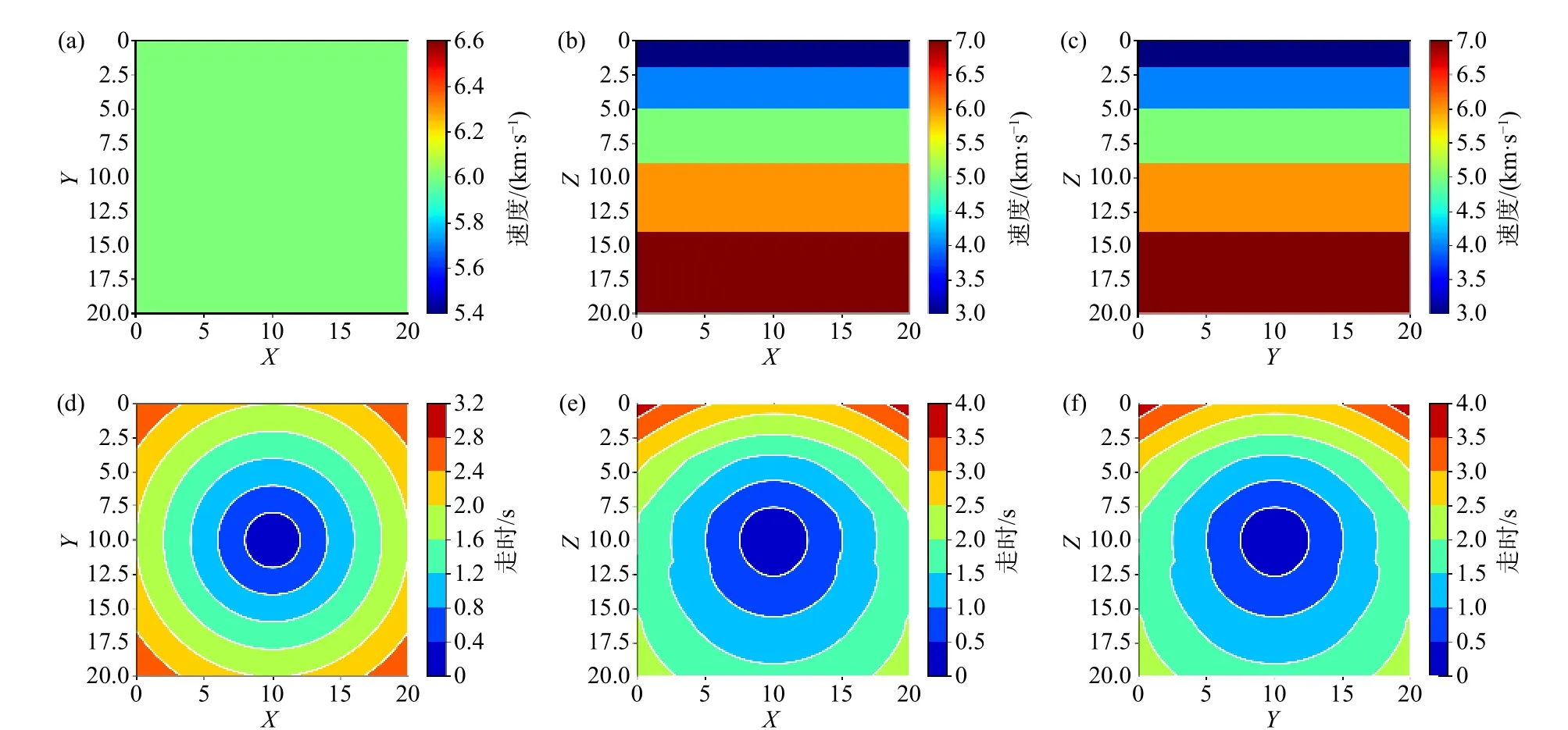

图 7 EikoNet 方法的走时计算结果. （a）、（b）、（c）和（d）、（e）、（f）依次代表速度模型和走时的X-Y、X-Z 和Y-Z 切片Fig. 7 The traveltime result of the EikoNet. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices of the velocity model and the travel time

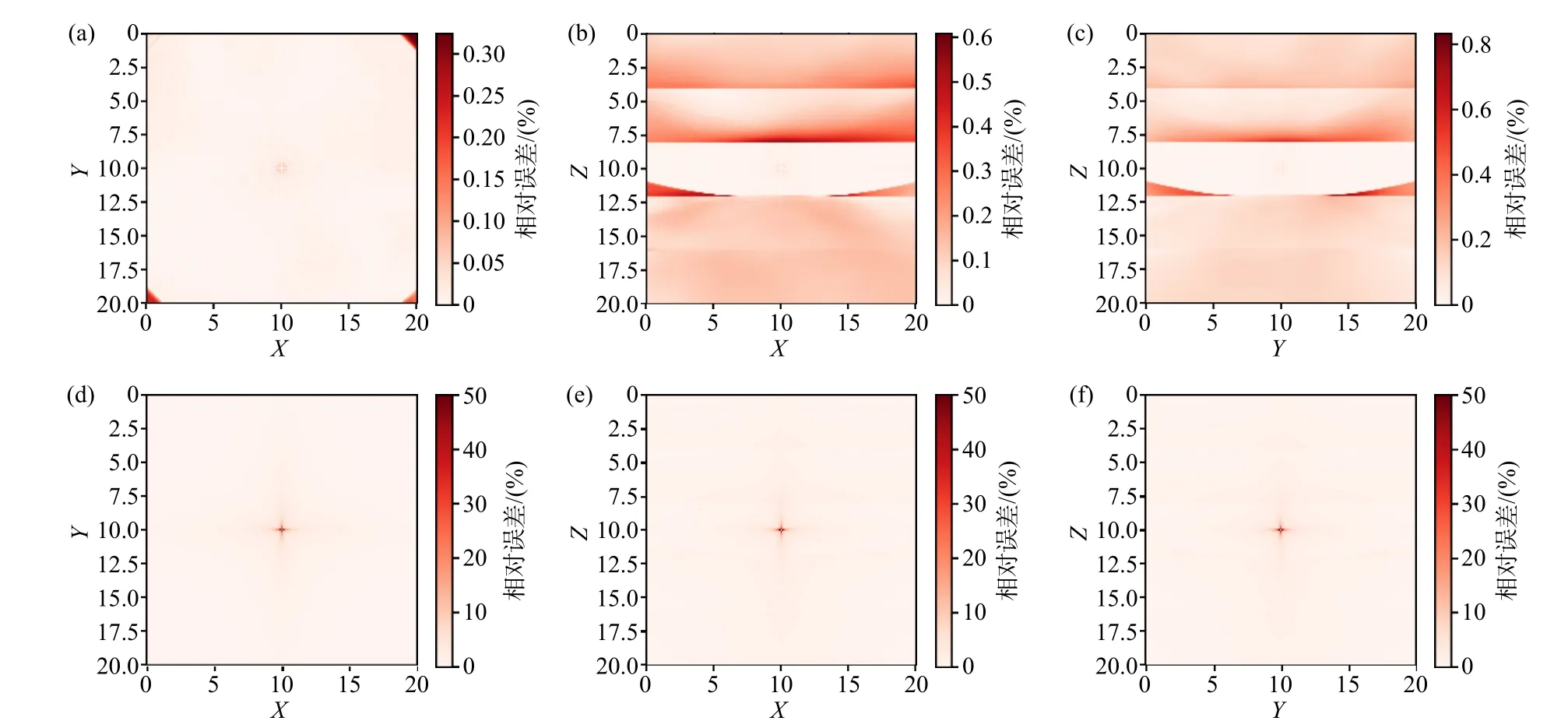
图 8 层状速度模型走时计算相对误差. （a）、（b）、（c）和（d）、（e）、（f）依次代表EikoNet 走时计算相对误差和FMM 走时计算相对误差的X-Y、X-Z 和Y-Z 切片Fig. 8 The relative error of the traveltime calculation of the layered model. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices ofthe relative error of the EikoNet and the relative error of the FMM

（4）棋盘格速度模型

设置模型的背景速度为5 km/s，在其中增加了速度扰动，扰动的振幅为1 km/s，模型的速度在4～6 km/s 之间变化，震源放置在（10 km, 10 km,0.1 km），图9 以二维切片的形式展示了EikoNet的走时计算结果. 从图10 可以看出，即便在速度正负变化较多棋盘格速度模型中，EikoNet 方法也较好地控制了误差，相对误差平均值为0.31%，FMM 误差分布则与前几个模型类似，相对误差平均值为0.58%. EikoNet 方法和FMM 的计算耗时分别为6.06 s 和31.70 s，效率比为5.23.

3 结 论

本文引入了基于深度神经网络进行程函方程走时计算的EikoNet 方法，通过速度模型实验，将其与快速推进法（FMM）进行了计算精度和效率的对比，结果表明：

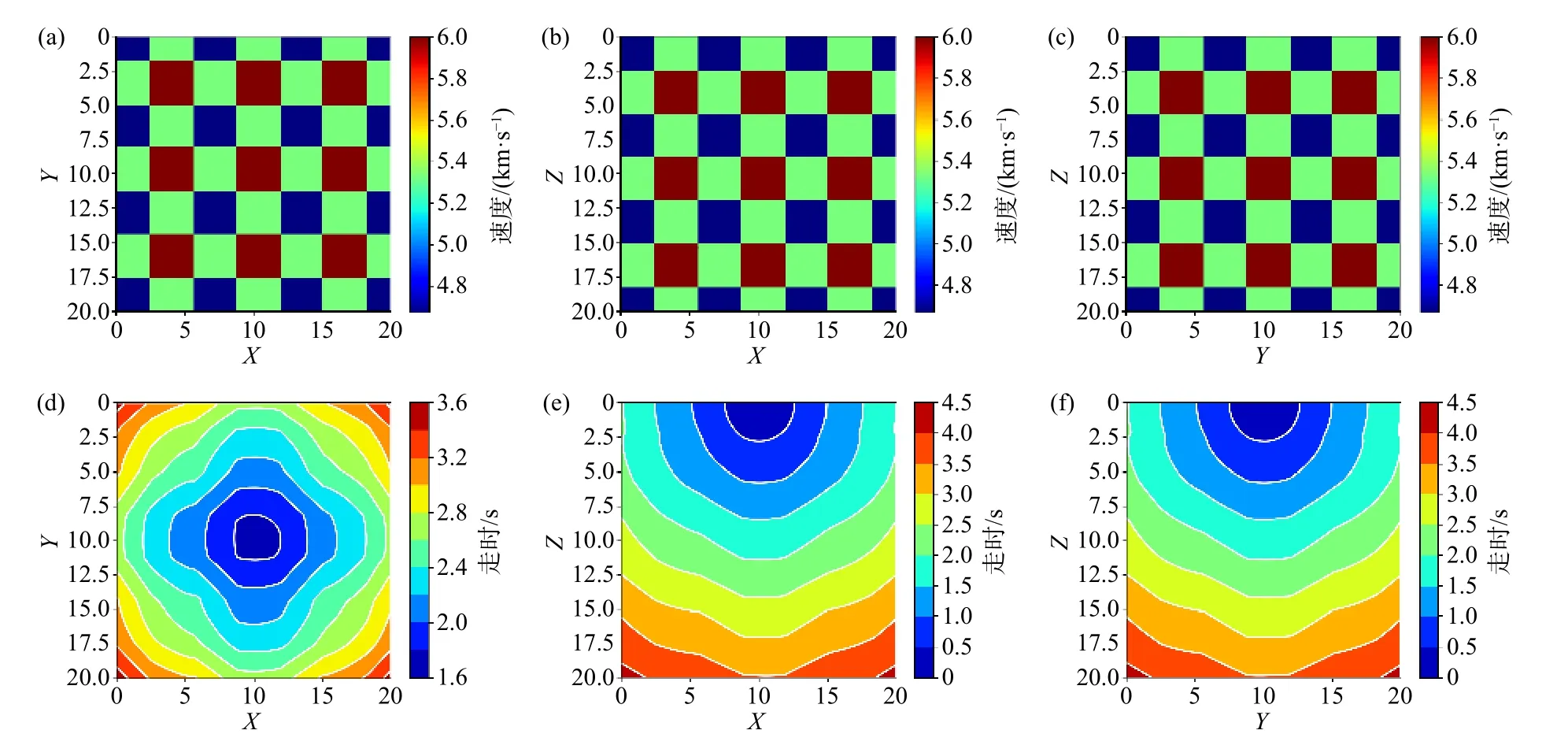
图 9 EikoNet 方法的走时计算结果.（a）、（b）、（c）和（d）、（e）、（f）依次代表速度模型和走时的X-Y、X-Z 和YZ 切片Fig. 9 The traveltime result of the EikoNet. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices of the velocity model and the travel time

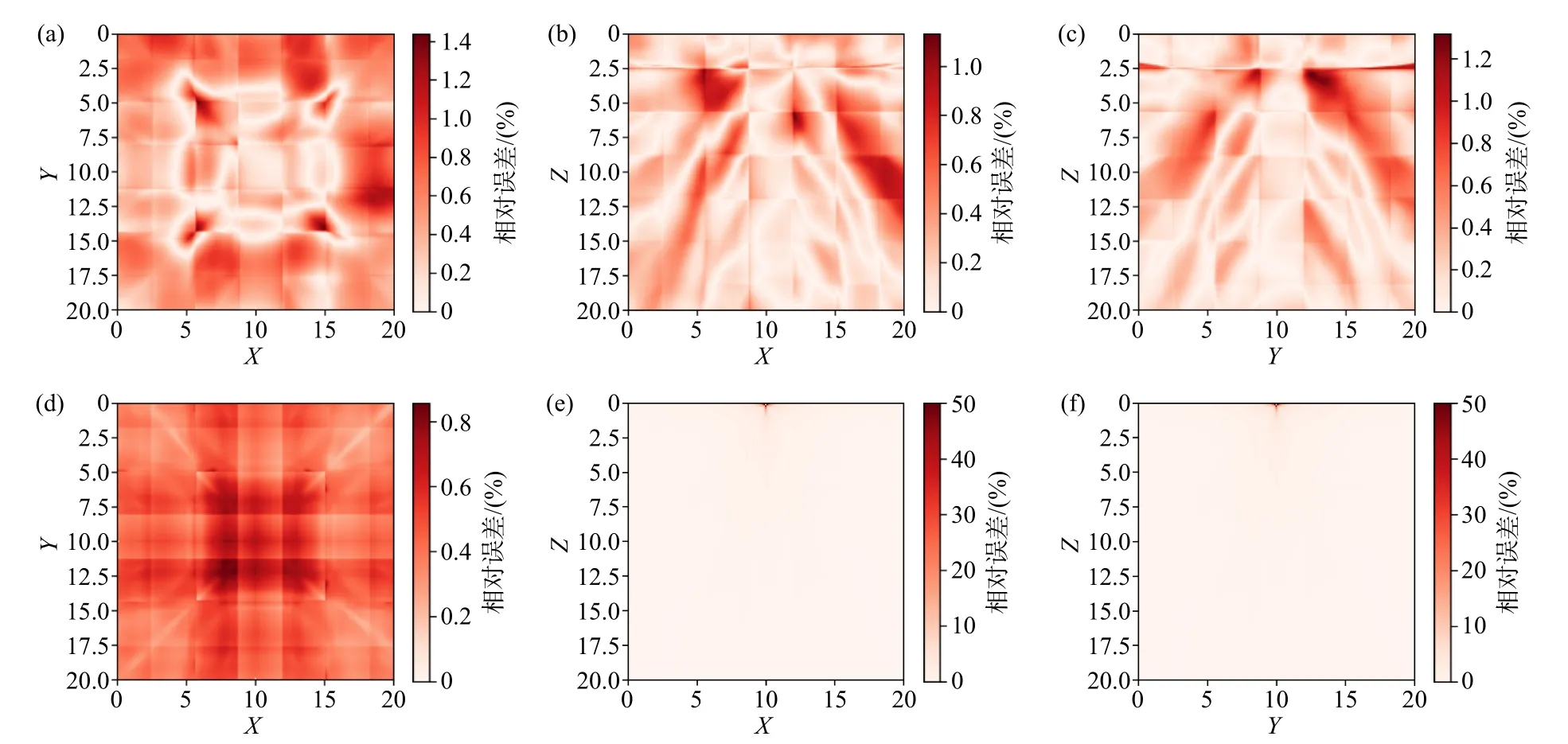
图 10 棋盘格速度模型走时计算相对误差. （a）、（b）、（c）和（d）、（e）、（f）依次EikoNet 走时计算相对误差和FMM 走时计算相对误差的X-Y、X-Z 和Y-Z 切片Fig. 10 The relative error of the traveltime calculation of the checkerboard model. (a), (b), (c) and (d), (e), (f) represent the X-Y, X-Z and Y-Z slices ofthe relative error of the EikoNet and the relative error of the FMM from top to bottom

（1）EikoNet 方法可以无网格地快速确定三维空间内任意两点之间的走时，计算速度是FMM 的4～5 倍，计算精度也相对更高.

（2）EikoNet 方法的训练和预测都是大规模并行的，计算走时只需要加载训练好的神经网络参数即可，无需存储模型的速度文件，大大降低了内存空间.

但是，文中仅使用EikoNet 方法在几种简单的速度模型上进行了尝试，在起伏界面等较为复杂的速度模型上的适用性还需要进一步研究.

致谢

感谢中国科学院地质与地球物理研究所兰海强副研究员和周小乐博士提供的因式分解程函方程走时计算结果. 感谢中国地震局地球物理研究所李永华研究员、张风雪研究员以及刘有山副研究员的建设性意见. 感谢三位匿名审稿人的宝贵建议，对稿件质量提升帮助很大.

附中文参考文献

韩卫雪，周亚同，池越. 2018. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探，57（6）：862-869.

兰海强，张智，徐涛，等. 2012. 地震波走时场模拟的快速推进法和快速扫描法比较研究[J]. 地球物理学进展，27（5）：1863-1870.

李飞，徐涛，武振波，等. 2013. 三维非均匀地质模型中的逐段迭代射线追踪[J]. 地球物理学报，56（10）：3514-3522.

林吉焱，唐国彬，徐涛，等. 2020. 钦杭—武夷山成矿带上地壳速度结构与基底特征: 万载—惠安宽角反射/折射地震剖面约束[J].地球物理学报，63（12）：4396-4409.

刘国峰，刘洪，李博，等. 2009. 山地地震资料叠前时间偏移方法及其GPU 实现[J]. 地球物理学报，52（12）：3101-3108.

徐涛，徐果明，高尔根，等. 2004. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报，47（6）：1118-1126.

徐涛，张明辉，田小波，等. 2014. 丽江—清镇剖面上地壳速度结构及其与鲁甸

M

6.5 级地震孕震环境的关系[J]. 地球物理学报，57（9）：3069-3079.

徐涛，张忠杰，刘宝峰，等. 2015. 峨眉山大火成岩省地壳速度结构与古地幔柱活动遗迹: 来自丽江—清镇宽角地震资料的约束[J].中国科学：地球科学，45（5）：561-576.

杨旭，李永华，盖增喜. 2021. 机器学习在地震学中的应用进展[J].地球与行星物理论评，52（1）：76-88.

张明辉, 刘有山, 侯爵, 等. 2019. 近地表地震层析成像方法综述[J].地球物理学进展, 34(1): 54-69.

赵明，陈石，Yuen D. 2019. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报，62（1）：374-382.

周小乐，兰海强，陈凌，等. 2020. 曲线坐标系因式分解程函方程及其走时计算[J]. 地球物理学报，63（2）：638-651.