基于IWOA-FLN的风电功率区间预测方法

张德望，陈智耿，张志超 ，周裕

（1.海南师范大学信息科学技术学院，海南 海口 571158；2.华能海南清洁能源分公司，海南 海口 572000）

随着全球能源互联网战略的快速高效实施，我国风电、光伏等可再生能源发电规模和消纳能力不断增加。近年来，能源消耗以及环境污染等问题的关注度越来越高，加快新能源发电技术的发展势在必行。风能作为一种清洁能源已成为各国最受关注的可再生能源之一。风力发电的出力受外界环境影响较大，当风电场大规模接入电网时，容易给电网频率调节和功率平衡带来不利影响。目前，国内外的学者对风电功率预测已开展了大量的研究，主要的预测方法包括时间序列模型、人工神经网络、支持向量机、灰色理论等[1-6]。这些预测方法通常用于输出功率点的预测，由于风力时间序列具有非平稳性、随机性的特点，输出功率点的预测误差难以完全消除。

功率区间预测可以量化不确定因素引起的误差，预测值以一定的概率落在预测区间内，根据预先制定的置信度以及预测区间的带宽可以有效地评价预测区间的准确性和可靠性。常用的区间计算方法包括回归分析理论、贝叶斯方法和Bootstrap等。文献[2]使用点回归分析理论，通过支持向量机自适应地选取回归函数，建立风电功率分位点回归模型，实现了对未来时刻风电功率的波动区间分析。文献[3]提出了基于朴素贝叶斯的正态指数平滑法和混合滑动核密度估计的组合风电功率区间预测方法。文献[4]提出了基于极端学习机（extreme learning machine，ELM）和Paris Bootstrap的预测模型，上述方法计算量大，模型较为复杂。文献[5]提出了基于神经网络的上下限估计（lower upper bound estimation，LUBE）区间预测方法。文献[6]提出一种基于双向长短期记忆网络和Bootstrap的组合预测模型，从网络结构上进行了改进。

快速学习网（FLN）是一种新型双并联前馈神经网络，FLN的输出层神经元不仅可以接收来自隐藏层神经元的信号，还可以从输入层神经元获得相关的信息[7]，具有更好的学习能力。针对神经网络模型参数的优化方法，典型的群智能优化算法包括粒子群算法（particle swarm optimization，PSO）、蚁群优化算法、人工鱼群优化算法、萤火虫算法等。鲸鱼优化算法（WOA）是2016年Mirjalili等学者受到座头鲸捕食行为的启发提出的一种元启发式智能寻优算法，该算法根据座头鲸捕食时的行动策略，利用包围猎物、随机搜索和螺旋包围3种方式来更新每头座头鲸的位置，从而包围猎物[8]。针对WOA容易陷入局部最优、收敛速度慢等问题，文献[9]通过柯西变异算子提高了鲸鱼算法的全局搜索能力，并加入自适应权重提高局部搜索能力。文献[10]通过正态变异算子和自适应惯性权重提高算法的寻优能力。文献[11]使用混沌反向学习策略初始化种群，在每代最优个体的基础上进行混沌搜索，对收敛因子进行改进并加入了惯性权重以提高算法的寻优能力。文献[12]使用非线性惯性权重，并对鲸鱼螺旋包围公式进行改进，采用差分变异微扰因子增加种群多样性。在前人的基础上，本文采用非线性收敛因子，并加入自适应惯性权重和混沌搜索策略对原算法进行改进，提出了改进型鲸鱼优化算法（improved whale optimization algorithm，IWOA）。

结合FLN的学习能力，本文提出基于改进型鲸鱼优化算法和快速学习网的风电功率区间预测模型IWOA-FLN。首先针对WOA的共性问题，提出了改进型鲸鱼优化算法，然后使用IWOA优化FLN模型参数以得到最终的预测区间。为验证IWOA-FLN预测模型的有效性，最后以海南某风电场为例，通过Matlab进行仿真实验，实验结果验证了本文所提方法的有效性。

1 基本鲸鱼优化算法

鲸鱼优化算法中每头鲸鱼的位置都代表着一个可行解，座头鲸捕食的行为轨迹则为相应可行解的更新方式，主要分为3步：包围猎物、随机搜索以及螺旋包围。

1.1 包围猎物

1.2 随机搜索

座头鲸在搜索猎物时会根据其他座头鲸的信息进行移动，故其随机搜索的数学模型与包围猎物的数学模型类似，即

式中：Xrand(t)为第t次迭代时随机选取的一头座头鲸。

根据包围猎物和随机搜索的迭代公式，A的取值受α影响，随机从2线性减小至0。当|A|≥1时，迫使座头鲸远离猎物并随机选择一头座头鲸进行跟随；当|A|＜1时，座头鲸向当前最优个体靠近。迭代初期A在[-2，2]区间内随机产生，随着迭代次数增加，A的取值逐渐减小至0。

1.3 螺旋包围

座头鲸在捕食期间以螺旋前进的方式包围猎物，其数学模型为

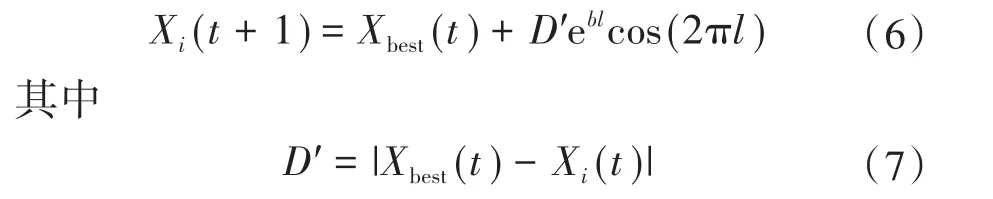
式中：b为螺旋包围常数；l为(-1,1)之间的随机数；D′为当前个体到最佳个体的距离。

在捕食过程中，座头鲸螺旋前进包围猎物，因此收缩包围和螺旋包围两种情况同等概率发生，故以p=0.5为概率阈值来决定个体下一次的迭代公式。

2 改进型鲸鱼优化算法

2.1 非线性收敛因子

鲸鱼个体搜索和包围猎物的过程很大程度依赖于参数α的变化，其决定了鲸鱼个体靠近最优个体的步长，较大的α会使个体在算法前期能更快地靠近最优解，但会在最优解附近来回震荡，而较小的α则使得算法收敛速度过慢。在基本鲸鱼优化算法中，当||A≥1时，鲸鱼个体可能远离猎物，保持较好的全局搜索能力；当||A＜1时，鲸鱼个体靠近最优个体实现更高的寻优精度，提高局部搜索能力。

原算法使α从2线性减小至0，该线性变化使得算法收敛速度过慢，不能完全体现鲸鱼优化算法的寻优能力。本文借鉴Sigmoid函数的变化特性，重新定义非线性收敛因子，使算法能够快速收敛，从而改善鲸鱼优化算法的寻优精度，非线性收敛因子α定义为

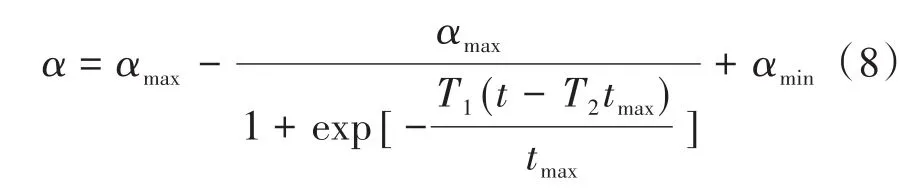
式中：αmax，αmin分别为收敛因子的最大值和最小值；T1，T2为大于零的常数，用于控制收敛因子减小的时间。

图1为改进前后α的取值波形，可见通过不同的T1，T2取值能够调整算法的收敛速度和收敛时间。经过多次测试，本文设置αmax=2，αmin=0.05，T1=20，T2=0.1。

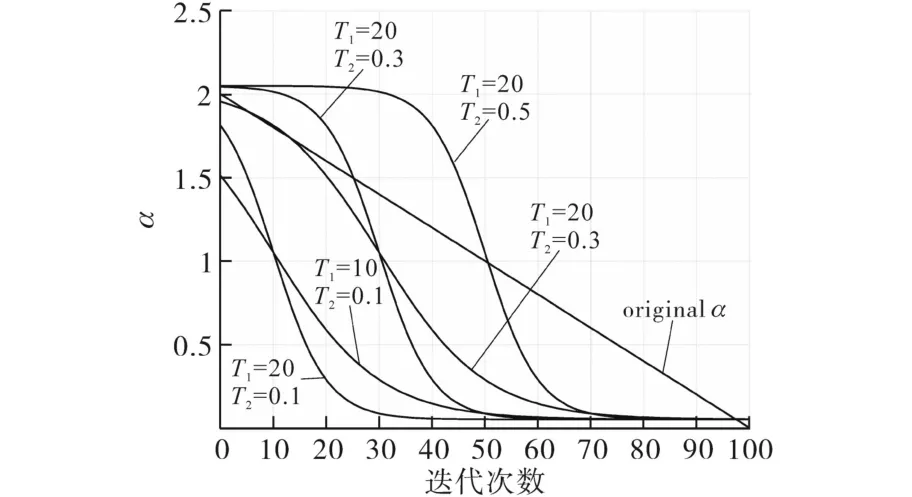
图1 α取值对比Fig.1 Comparison of the value of α

2.2 自适应混沌搜索策略

2.2.1 混沌搜索策略

混沌策略表现出了很强的随机性，可以利用该特性提高算法中种群的多样性，使得鲸鱼个体能够摆脱局部最优解。常用的混沌搜索策略有Logistic映射和Tent映射，Tent映射比Logistic映射有遍历更均匀的特性。鲸鱼算法在随机搜索时会随机挑选一个鲸鱼个体向其靠近，当种群出现“早熟”现象时原算法的随机搜索也很难跳出局部最优解，因此本文使用Tent映射替代原算法中的随机搜索，Tent映射函数表达式为

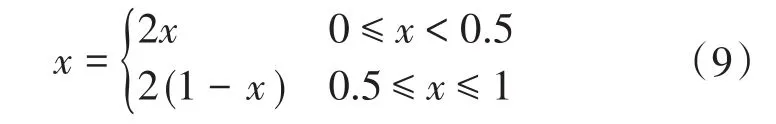
迭代开始前随机生成一个鲸鱼个体Xc，该个体不跟随种群进行捕猎，而是通过Tent映射随机搜索。当种群中的鲸鱼个体进行随机搜索时不再随机选择种群中的某一个体，而是改向Xc靠近，以此提高算法的种群多样性，提高跳出局部最优的概率，因此将式（6）修改为

式中：F为一个常系数，其作用是增大步长以便于鲸鱼个体跳出局部最优，本文设置F=30。

2.2.2 搜索概率自适应调整

在2.1节中，通过修改收敛因子使得算法能够快速收敛，但容易出现“早熟”现象，因此，本文采用自适应搜索概率，其表达式为

式中：k为正整数，用于调节搜索概率，本文设置k=3；fi为当前第i个个体的适应度；fmin，fmax分别为当代种群中最优个体和最劣个体的适应度。

Pc的大小和个体适应度相关，因此在整个迭代过程中使得优质个体能以较大的概率继续向最优个体靠近，而劣质个体则以较大的概率向Xc靠近，从而增加种群多样性。

2.3 自适应惯性权重

惯性权重是粒子群算法（PSO）的重要参数，当惯性权重较大时表征粒子具有更大范围的搜索能力；当惯性权重较小时，则表征粒子小范围搜索能力强，算法后期可以有效提高寻优精度。本文借鉴PSO算法加入自适应惯性权重，分为线性权重和自适应权重两部分，其表达式为

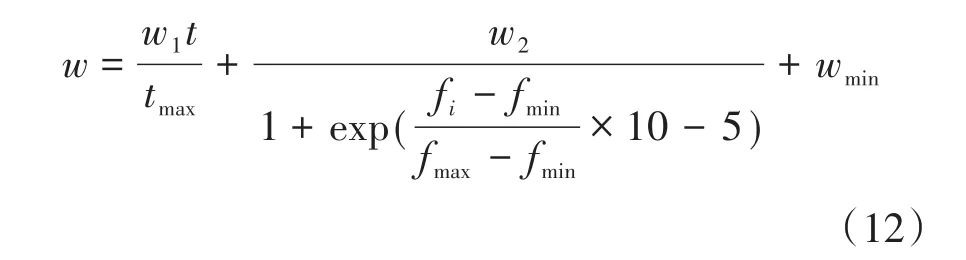
式中：w1为线性权重的最大值；w2为自适应权重的最大值；wmin为最小惯性权重。

与粒子群算法不同的是，鲸鱼优化算法的位置更新公式是以最优个体为基础，因此自适应惯性权重加在最优个体上。线性部分的权重随着迭代次数增加由0线性递增至w1；自适应部分的权重则根据当前个体适应度进行计算权重，当前个体适应度越小，则对应的自适应部分的权重越大，反之则自适应部分的权重较小。在算法前期，由于线性部分的权重较小，使得鲸鱼个体能够与最佳个体保持一定的搜索距离以避免过早陷入局部最优；在算法后期，线性部分的权重逐渐增大，同时离最佳个体较近的鲸鱼个体自适应部分的权重也较大，从而使其能够在最佳个体附近进行搜索，提高寻优精度。加入自适应惯性权重后的位置更新公式为

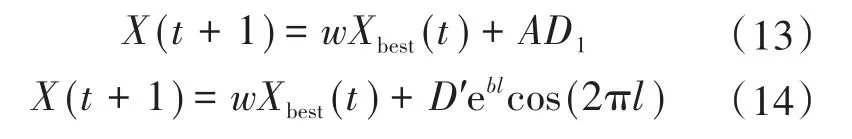
2.4 改进型鲸鱼优化算法执行流程

综上所述，改进型鲸鱼优化算法（IWOA）流程如图2所示。

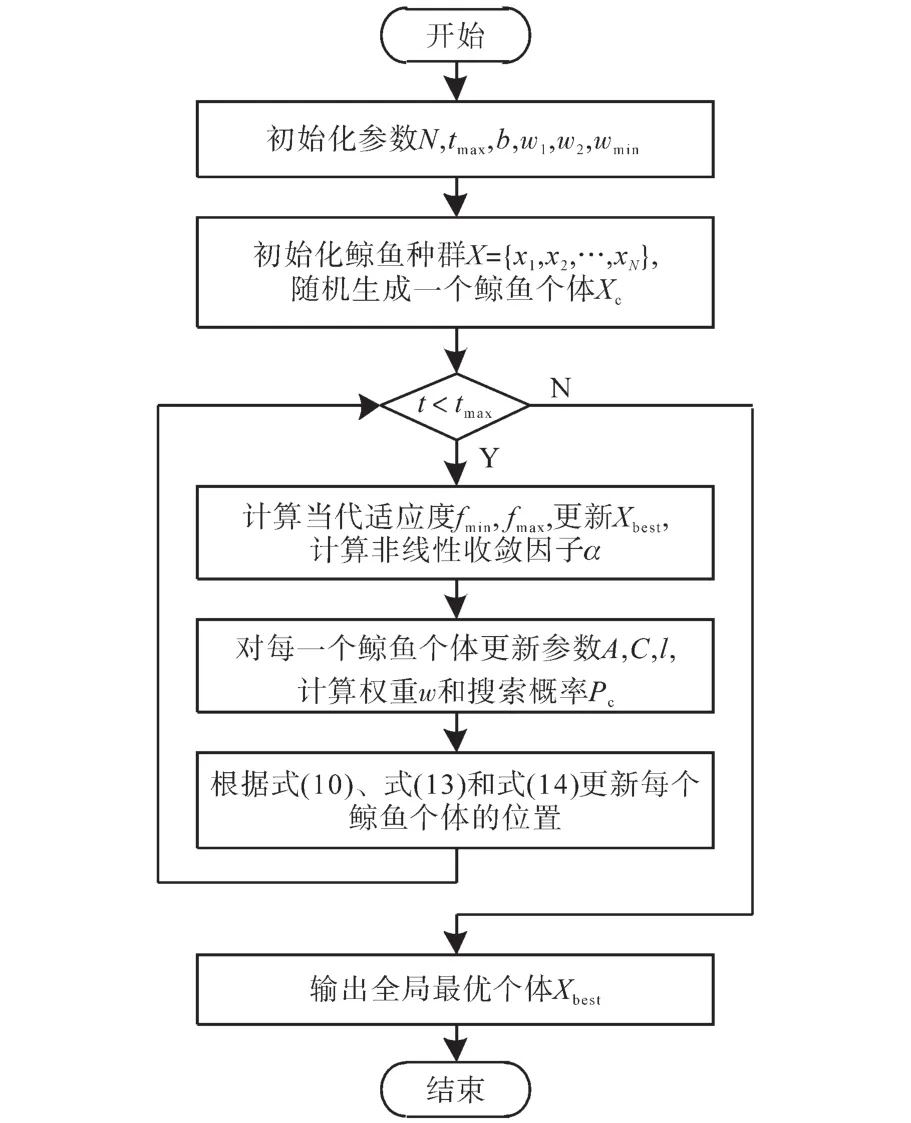
图2 IWOA算法流程图Fig.2 Flow chart of improved whale optimization algorithm

2.5 改进型鲸鱼优化算法（IWOA）测试

为验证IWOA的性能，本文使用6组常用的测试函数进行测试，测试函数如表1所示，结果对比如表2所示。文献[10]已经验证了基本鲸鱼算法要优于粒子群算法、引力搜索算法和差分进化算法，本文不再重复。仿真使用Matlab 2013b进行编程，计算机操作系统为Win10操作系统，CPU为I5-6300H，内存为12 G，主频为2.3 GHz。

表1 测试函数Tab.1 Test functions

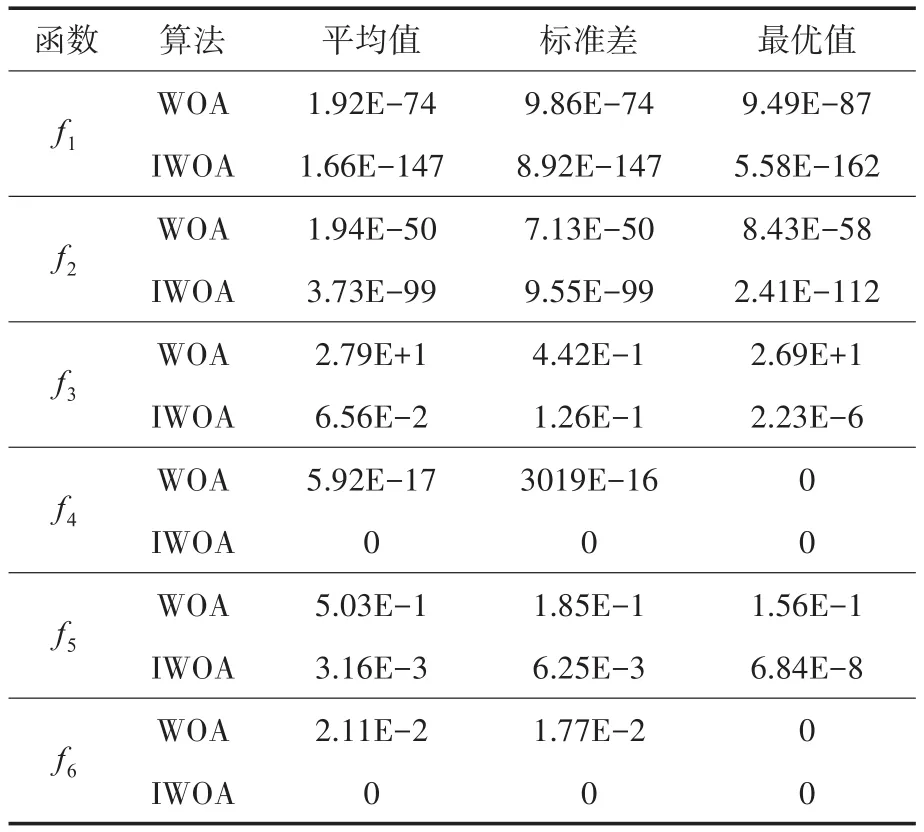
表2 测试结果对比Tab.2 Comparison of test results

种群规模N=30，迭代次数tmax=500，IWOA基本参数设置为：b=1，w1=w2=0.4，wmin=0.2。测试函数维度均为30，独立运行50次，计算运行结果的平均值、标准差和最优值。

从表2可以看出，本文所提的IWOA算法在6种函数的寻优过程中表现均好于WOA算法。对于f1，f2，f3和f5来说，虽然未达到理论最优值，但相较于WOA在寻优精度上有了很大的提高；对于f4和f6来说，50次独立实验均能收敛至理论最优值，表示IWOA算法有较高的寻优效率和较好的鲁棒性。

3 IWOA-FLN风电功率区间预测模型

3.1 基于LUBE的FLN模型

上下限估计方法是一种直接构造预测区间的非参数方法，使用双输出的网络模型，两个输出分别对应区间的上界和下界。本文基于LUBE上下限估计法，采用FLN快速学习网构造预测模型，如图3所示。

图3 基于LUBE的FLN模型Fig.3 The model of FLN based on LUBE

图中，xi为1×n的矩阵，表示输入向量；wih为n×m的矩阵，表示输入层神经元与隐含层神经元之间的权重；b为1×m的矩阵，表示隐含层神经元的偏置；who为m×2的矩阵，表示隐含层神经元与输出层神经元之间的权重；wio为n×2的矩阵，表示输入层神经元与输出层神经元之间的权重；yU，yL分别为输出的上界和下界。FLN的输出函数可描述为

式中：g(·)为隐含层神经元的激活函数。

其中，输入层神经元与隐含层神经元之间的权值win和偏置b在训练前随机生成，在之后的训练过程中作为常数不再更新。

3.2 预测区间目标函数

预测区间的构造是在一定置信度下估计区间的上界和下界，表明该区间的评价需要从准确性和质量两个方面考虑[13]。为评价区间的准确性，引入预测区间覆盖率（predict interval coverage probability，PICP），定义为

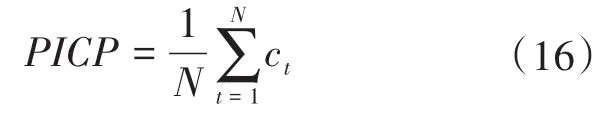
式中：N为预测点总数。当实际目标值处于预测区间内时ct=1，否则ct=0。PICP∈[0,1]，越接近1，表明区间准确率越高，反之越低。

为评价预测区间的质量，引入预测区间均方根带宽（predict interval normalized root-mean-square width，PINRW），定义为

式中：yUt，yLt分别第t个预测点预测区间的上界和下界；R为目标值的变化范围，用于平均带宽的归一化处理，当区间覆盖率一定时，平均带宽越接近0，表明区间预测质量越高，反之越低。

文献[14]提出了一种综合覆盖率和区间带宽的覆盖宽度准则（coverage width-based criterion，CWC），将复杂的多目标问题转化为单目标问题，定义为

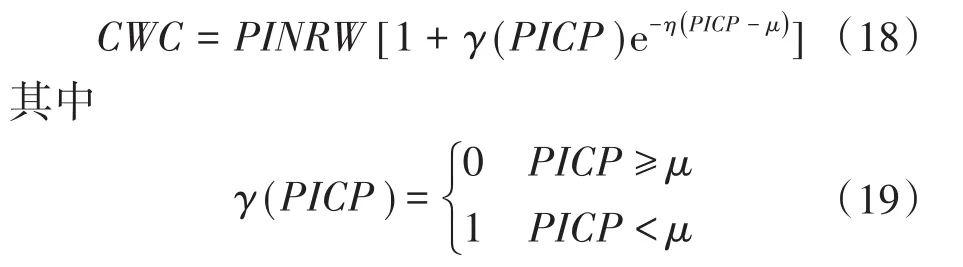
式中：μ为规定的置信度；η为覆盖率小于置信度时的惩罚系数。

CWC兼顾了覆盖率和区间带宽，但并没有对实际功率曲线在预测区间的位置进行评价，因此本文加入预测区间偏差（predict interval deviation，PID）指标，定义为

将预测区间偏差PID加入原CWC，重新定义目标函数为

式中：η1为覆盖率小于置信度时的惩罚系数；η2为预测区间偏差的惩罚系数。

当输出的预测区间满足规定的置信水平时，式（21）中第1项为0，此时优化目标为PINRW和PID；若不满足置信水平，则相应的个体在训练过程中由于较大的惩罚系数的作用会被舍弃。新的目标函数F不仅能兼顾覆盖率，同时也兼顾了预测区间的带宽和偏离情况，提高预测区间的质量。

3.3 优化区间预测模型步骤

IWOA-FLN的风电功率区间预测模型步骤如下：

1）数据预处理。去除数据集中的停机点，将数据归一化至[0,1]，避免不同量纲的数据造成的误差。

2）构造训练样本集合。设定输入数据为X={x1,x2,x3,x4,x5,x6}，其中x1～x4为前4个时刻的风电功率数据，x5，x6分别为预测点的温度和风速。

3）构造区间预测模型。确定隐含层神经元节点数量，随机生成FLN模型输入层神经元到隐含层神经元的权值和偏置，构造待优化参数向量。

4）优化预测模型。使用IWOA算法优化模型参数，即隐含层神经元到输出层神经元的权重和输入层神经元到输出层神经元的权重构成的向量。

5）计算预测区间。使用优化后的模型参数进行计算，从而得到预测区间。

4 仿真及结果分析

以海南某风电场为例，该风电场使用机型为1.5 MW双馈异步风机，实测数据间隔为10 min，共选取5 000个数据点，使用实测数据的90%作为训练集，10%作为测试集。为验证本文所提预测模型的有效性，使用PSO，WOA和IWOA对FLN模型进行优化，3种算法分别对同一模型和训练集独立运行10次，最后将最优的参数用于测试集进行测试。FLN模型设置输入层6个神经元，隐含层10个神经元，输出层2个神经元，使用Sigmoid函数作为隐含层的激活函数。因风电输出功率区间的非负性，因此使用ReLU函数对输出层神经元进行激活。迭代次数M=300，种群规模N=50，惩罚系数η1=100，η2=0.2。

图4为置信度为90%时PSO，WOA和IWOA优化FLN模型的适应度收敛曲线。从图中可以看出PSO在60代左右时便收敛到了局部最优解。WOA未陷入局部最优，但其收敛速度较慢。IWOA在非线性收敛因子的作用下能够快速收敛，同时由于加入了自适应惯性权重和混沌搜索策略，使得IWOA能够很容易跳出局部最优解。

图4 置信庞为90%的适库庞收敛曲线Fig.4 Convergence curves of fitness value for 90% confidence

表3给出了三种模型在相同数据集下，置信度为90%和80%的各项指标。从测试指标来看，三种模型的PICP指标均高于规定值，这是因为FLN具有较好的泛化能力，以及在优化模型参数时由于PID指标的存在使得预测区间中点尽可能接近实际的输出功率值，因此即使输出功率和预测区间中点有所偏差也能大概率落在预测区间内。对比分析置信度为90%时IWOA-FLN的PICP指标仅比PSO-FLN和WOA-FLN低了0.7%和0.6%，置信度为80%时IWOA-FLN的PICP指标比PSO-FLN高了0.8%，而比WOA-FLN仅仅低了1.4%，同时PINRW和PID指标都低于其它两者，说明IWOA-FLN在满足规定置信度的前提下，具有更窄的预测区间带宽以及实际输出功率偏移预测区间中心点的程度最低。

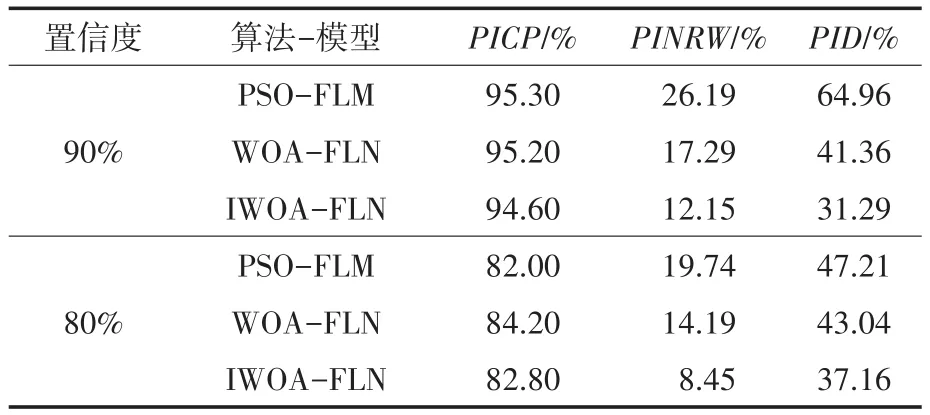
表3 3种模型的评价指标Tab.3 Evaluation index of 3 models

置信度为90%的前提下，三种模型输出的预测区间如图5～图7所示。

图5 置信庞为90%的PSO-FLN预测区间Fig.5 Prediction interval of PSO-FLN for 90% confidence

图6 置信庞为90%的WOA-FLN预测区间Fig.6 Prediction interval of WOA-FLN for 90% confidence

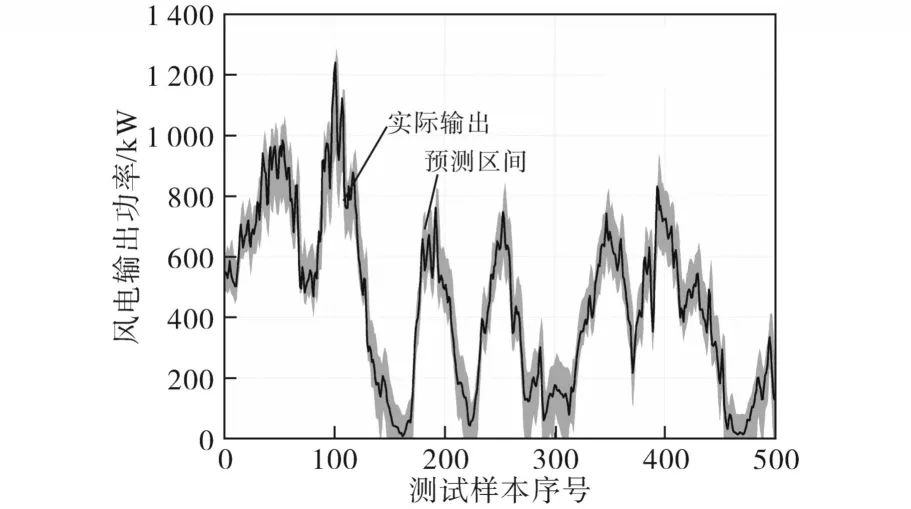
图7 置信庞为90%的IWOA-FLN预测区间Fig.7 Prediction interval of IWOA-FLN for 90% confidence

在三种预测模型的仿真结果中，图5的纵坐标数值范围大于图6和图7的数值范围，易于看出PSO-FLN的预测能力最差。对比图6和图7可以看出在置信度为90%的前提下IWOA-FLN预测模型输出的预测区间带宽更窄，实际输出功率基本落在预测区间内。由于预测区间偏差项PID指标的存在，即使实际输出功率落在预测区间外也不会偏移过远。从整体来看，本文所提IWOAFLN模型的预测效果更佳，对决策者的分析和操作具有一定的指导意义。

5 结论

本文针对基本鲸鱼算法的缺点进行了改进，很大程度上提高了鲸鱼优化算法的寻优能力。构建了基于快速学习网的风电功率区间预测模型，改进区间预测目标函数，提高预测区间的质量。通过本文所提的改进鲸鱼优化算法来优化区间预测模型中的参数，并在测试集中验证了IWOA-FLN的预测能力。