蓝宝石超精密研磨工艺决策支持系统的研发
何勇,万林林
(湖南科技大学 a. 智能制造研究院, b. 难加工材料高效精密加工湖南省重点实验室,湖南 湘潭 411201)
0 引言
绿色制造是综合考虑资源消耗和环境保护的现代制造模式[1]。制造工艺决策技术以及工艺数据库作为绿色制造领域的关键技术,受到了国内外众多学者的持续关注。李联辉等[2]提出了基于可拓分析及D-S理论的工艺规划方案评估方法,并运用实例对该方法进行了验证。LV L等[3]提出机床工艺参数多目标决策方法,并通过磨削实验验证了该方法的有效性。伍晓榕等[4]运用决策试验与评价实验室方法确定指标权重,并采用VIKOR方法对绿色工艺参数进行选优。钟君焐等[5]建立了基于BP神经网络算法的加工方法和刀具选择决策模型,并通过实验验证了该模型的有效性。何彦等[6]开发了面向绿色制造的工艺规划支持系统,该系统能实现工艺要素选择、工艺优化及工艺绿色性能评价等功能。赵曦[7]开发了热处理工艺评价系统,构建了面向热处理工艺的基础数据库,并通过神经网络对模型进行训练和验证。钟健[8]开发了面向低碳制造的数控滚齿工艺参数决策支持系统,该系统可降低数控滚齿加工过程的碳排放量,并提高工艺参数决策效率与精度。
从以上文献可以看出:1)工艺决策技术的研究在指标赋权方面有所欠缺,大都只偏向于主观权重或客观权重,没有将其综合考虑在内;2)综合考虑制造资源环境属性指标的工艺数据库研究较少,特别是对于蓝宝石企业,缺乏有效的、能对蓝宝石超精密研磨工艺资源环境属性数据进行科学分析及工艺方案决策选优的数据库系统,这是亟待解决的问题。
鉴于此,本文设计了一种主客观综合赋权的工艺方案多属性决策方法,并通过实验验证了该方法的正确性。在此基础上,设计研发了一套蓝宝石超精密研磨工艺决策支持系统,存储工艺方案的资源环境属性等基础数据,并实现对有限工艺方案的多属性决策的选优,为企业提供合理、绿色高效的加工工艺方案,助力企业绿色制造水平的提升。
1 决策指标赋权
指标权重直接关系到指标对总体的重要度大小,因此,确定指标权重,是实现科学决策的前提。本文针对制造过程中各指标存在较强相关性且指标易存在特殊数据这一特点,提出CRITIC法与层次分析法综合主客观权重的分析方法。CRITIC法确定指标客观权重;层次分析法确定指标主观权重,以此修正指标特殊数据导致的客观权重偏差(因层次分析法使用较为普遍,故本文省略其计算步骤);采用线性加权法对主观及客观权重进行综合,获得指标综合权重。
1.1 CRITIC法客观赋权
CRITIC法是由DIAKOULAKI D等[9]最先提出的一种考虑指标间相关性的客观定权法。该方法通过指标内的对比强度和指标间的冲突性来综合判定指标的客观权重。对比强度指同一指标不同方案的取值差异,用标准差来表示;指标间冲突性则基于指标间的相关性。CRITIC法进行客观赋权的步骤为:
1)构造原始数据矩阵X
X=[xij]m×n
(1)
式中:xij为X各元素;m(i=1,2,…,m)为工艺方案数;n(j=1,2,…,n)为指标数。
2)对X进行标准化
(2)
式中xjmax与xjmin分别为第j个指标的最大值及最小值。
3)计算指标标准差σj和相关系数Rkj
4)确定指标的信息量Cj
(3)
5)确定指标客观权重θj
(4)
1.2 指标综合赋权
主客观综合赋权法是定量与定性相结合的权重分析法,既能减少决策者的主观随意性,又能弥补客观赋权法的不足。令层次分析法求解的主观权重为λj,则指标综合权重ωj可以用如下公式进行求解:
ωj=μλj+(1-μ)θj
(5)
式中μ(0≤μ≤1)反映决策人员对权重的偏好,μ越大表明决策人员越倾向于主观权重。
2 加权TOPSIS法决策模型
指标赋权后,就可基于此采用合适的决策方法对各方案的指标值进行综合,进而对各工艺方案进行决策选优。TOPSIS法是典型的有限方案多属性决策法,该法计算简便、评估结果较合理、应用较为灵活[10]。因此,本文在获得指标权重基础上,运用TOPSIS法建立加权TOPSIS模型,实现对有限工艺方案的多属性决策,实现步骤如下:
1)对原始数据矩阵X进行向量规范化处理
(6)
2)构造加权规范化决策矩阵H
(7)
式中:hij为H各元素;ωj为指标综合权重。
3)确定正、负理想参考序列
(8)
(9)
(10)
(11)
4)分别计算各方案与正、负理想参考序列的距离Di+、Di-
(12)
5)计算各方案与正理想参考序列的相对贴近度Di,其值越大表明方案越优
(13)
3 蓝宝石超精密研磨工艺实验
为了验证所提出的工艺方案多属性决策方法的有效性,本研究开展了蓝宝石超精密研磨工艺实验,在采集各方案指标数据的基础上,采用该多属性决策方法对数据进行决策,进而选出最优方案。
3.1 实验方案设计
需选取的工艺参数有:研磨盘转速(r/min)、游星轮转速(r/min)、研磨时间(min)、研磨液流量(mL/min)。在YH2M8164B单面研磨机上进行实验,实验材料为直径49mm、厚度2mm的A向蓝宝石晶片及W-14-PC研磨液。采用万分之一克电子天平获取原材料消耗(g)、数字功率计并通过计算获取机床加工能耗(kWh)、流量计获取研磨液消耗(mL)、噪声测定仪获取噪声分贝数(dB)。公式计算获取材料去除率大小(nm/min),表面粗糙度仪获取蓝宝石表面粗糙度值(μm)。机床及关键设备如图1所示。

图1 机床及关键设备
3.2 实验数据处理与分析
按照前文所述实验方案,在单面研磨机上进行蓝宝石超精密研磨实验,采集各工艺方案的资源环境属性数据,见表1。
1)依据CRITIC法,求解得到指标客观权重:
θj=(0.13,0.13,0.14,0.17,0.20,0.23)
2)依据层次分析法,确定指标主观权重:
λj=(0.177,0.145,0.205,0.151,0.169,0.153)
3)取偏好系数μ=0.5,得指标综合权重:
ωj=(0.154,0.138,0.172,0.160,0.184,0.192)
4)计算各工艺方案到正、负理想参考序列的贴近度及相对贴近度:
Di=(0.645,0.814,0.767,0.378,0.486,0.397,0.541,0.54,0.566)
根据各方案的相对贴近度结果进行排序,排序结果见表1。
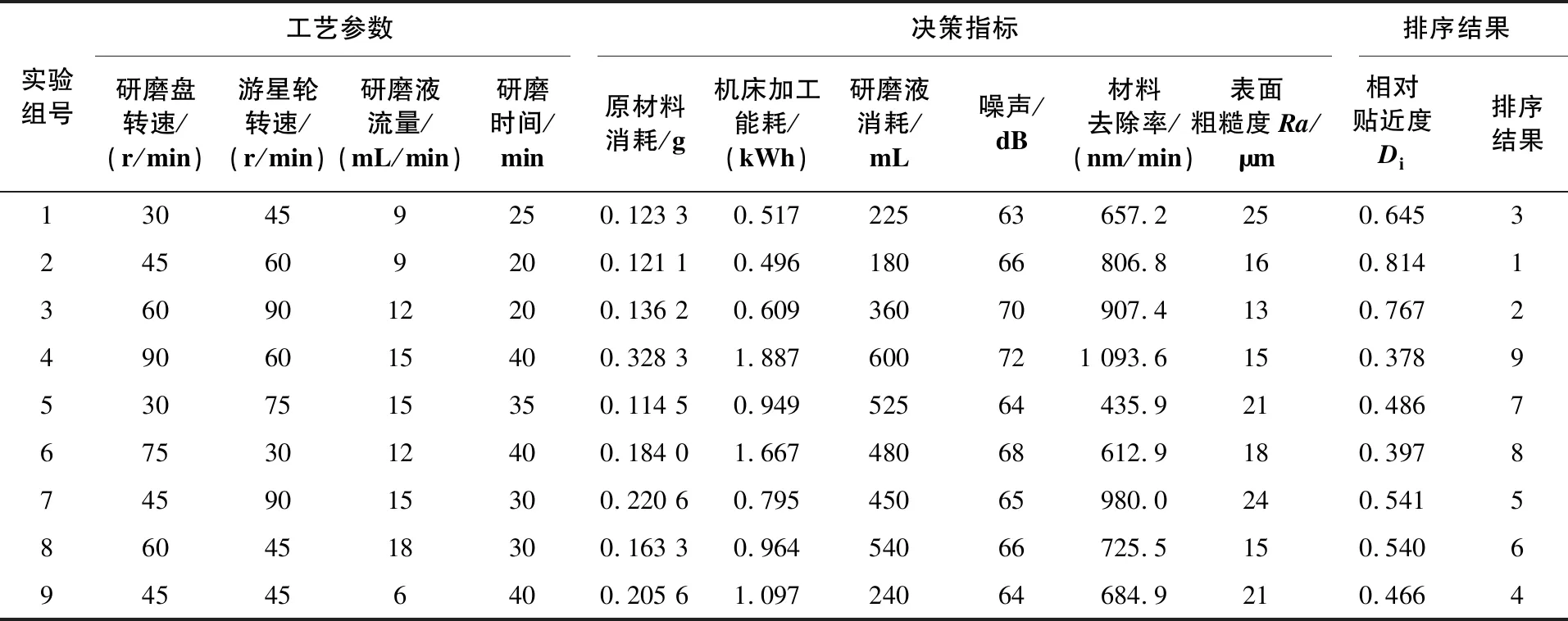
表1 工艺资源环境属性数据及方案排序结果
根据表1可知,第2组工艺方案为决策选优方案,其对应的原材料消耗为0.121 1 g、机床加工能耗为0.496kWh、研磨液消耗为180mL、噪声为66dB、材料去除率为806.8nm/min、表面粗糙度Ra为16nm。由此可知该决策方案在保证较大材料去除率及较低表面粗糙度的前提下,达到了减少原材料消耗、能耗、研磨液以及资源环境排放的目的,实现了制造业传统指标与资源环境属性指标的多目标优化,可为企业工艺决策人员的生产实践提供指导。
4 蓝宝石超精密研磨工艺决策支持系统结构设计
基于前文所设计的多属性决策方法,并经实验验证其科学性后,以快速准确地辅助工艺人员决策为出发点,设计并开发了蓝宝石超精密研磨工艺决策支持系统。
4.1 系统功能设计
该工艺决策支持系统主要包括基础数据库模块与工艺方案决策选优模块。基础数据库模块可以对研磨工艺资源环境属性等信息进行添加、删除、修改、查询。决策选优模块可以对研磨工艺方案实例进行决策,优选出最好方案以指导生产实践。系统结构体系如图2所示。

图2 决策支持系统的结构体系
4.2 系统运行流程
围绕此决策支持系统的两大功能模块,建立了此系统的工作流程,如图3所示。具体流程为:1)用户进入系统主界面;2)选择研磨工序;3)进入方案选优模块,通过权重模块和决策模块实现对研磨工艺方案的选优及排序;4)决策结果显示。

图3 系统运行流程图
4.3 系统运行效果
系统的主界面如图4所示。工具栏包含了各基础数据库,方便用户对各数据库进行相关操作。在工作区域,用户可通过选择超精密研磨工序,进入具体的功能界面。
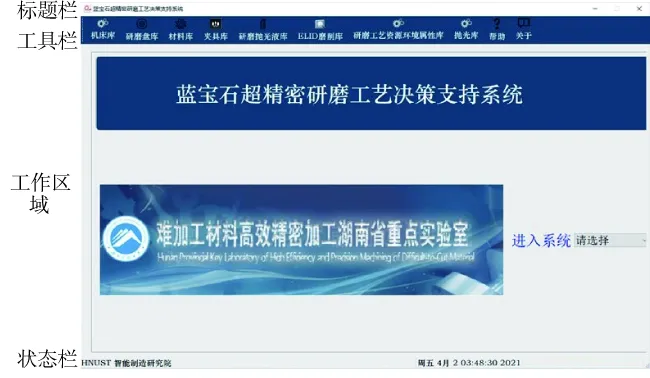
图4 决策支持系统主界面
工艺方案决策选优的主要操作界面如图5所示。系统录入了各研磨工艺方案的资源环境属性数据,通过系统的权重计算模块及多属性决策模块对各方案进行排序,并将结果进行显示。如图5所示,第2组工艺方案为最优工艺方案,其对应的工艺参数为:研磨盘转速45r/min,游星轮转速60r/min,研磨液流量9mL/min,研磨时间20min。可知该系统满足实际决策效果,减少了工艺决策的时间,提高了企业的工作效率。

图5 工艺方案决策选优界面
5 结语
1)将CRITIC法与层次分析法相结合进行指标赋权,决策结果既能体现主观信息,又能体现客观信息;在指标赋权基础上引入TOPSIS法建立多属性决策模型,通过蓝宝石超精密研磨实验,其模型可行性得到了验证,且该模型有一定的推广价值。
2)以设计的多属性决策方法为支撑,以蓝宝石超精密研磨作为研究对象,开发了蓝宝石超精密研磨工艺决策支持系统。该系统存储了蓝宝石超精密研磨各工艺方案的基础库信息及资源环境属性信息,可以实现对研磨工艺方案的决策选优,能够有效解决制造过程各指标的多目标优化问题,对企业绿色制造水平的提升有一定的辅助作用。

