基于时间序列神经网络的河流水位预测
刘 达,罗维平
基于时间序列神经网络的河流水位预测
刘 达,罗维平*
(武汉纺织大学 机械工程与自动化学院,湖北 武汉 430200)
针对我国每年频繁发生的洪涝灾害及河流航道通行困难等问题,构建了一个基于时间序列神经网络的高精度的河流水位预报模型,该模型能够有效预测河流水位值,进而及时做出应急处理,减少对生命财产造成的损失。该模型采用湖北省武汉市某水位站2019年7月29日至2020年5月28日的逐时水位时间序列作为训练样本进行训练, 2020年5月29日至2021年8月28日的逐时水位组成的500个数据为测试样本进行检验。该模型的预测水位值与真实水位值之间的平均绝对误差为0.00663,均方根误差为0.08143,平均绝对百分比误差为0.23785%,预测精度极高,具有较强实际应用前景。
BP神经网络;时间序列;水位预测
0 引言
我国洪涝灾害频发,2018年至2020年年均出现了34次暴雨天气过程[1-3],极易引发洪涝灾害,对社会秩序、经济发展、生命财产安全以及生态系统等方面造成极大的破坏,对受灾地区造成深远影响[4]。在此背景下,对经常遭受洪涝灾害地区主要河流的水位进行预测,在水位超过警戒值后进行预警就显得极为重要。河流水位数据是分析受灾流域范围的重要数据,提前进行河流水位的预报,能够及时有效的对汛情进行处置,做出提前进行人员转移、加固河堤等工作安排,保护人民的生命财产安全。河流水位预测也不仅仅只是用于防汛工作,对水路运输的安全通航也有着重大指导意义,航道尺度的大小取决于水位数值的高低,精确的水位预测可以进一步提升航道综合服务能力,提高航道通行能力,保障船舶安全航行等[5]。目前,航道部门通过设置水位观测站等方式,可以获取大量的水位数据。本文基于这些数据,建立一个时间序列的神经网络模型对河流水位进行预测研究。
1 研究现状
BP神经网络及其改进算法目前大量应用于水文信息预测研究。刘光星等[6]利用粒子群算法优化的BP神经网络对地下水位进行预测,该模型相比BP神经网络具有更好的收敛性,全局寻优能力更强,预测精度更高,其模型的平均绝对百分比误差为3.89%。马辉等[7]将灰色模型与BP神经网络进行组合对赣江外州水文站的水位进行预测,其平均误差为0.37%。韩卓慧等[4]将主成分分析法(Principal Component Analysis,PCA)引入基于遗传算法(Genetic Algorithm,GA)的BP神经网络构成PG-BP神经网络模型,将该模型对大沽河流域的汛期水位进行预测,其拟合精度较高,具有一定适用性,但得到的均方根误差仍为0.15。以上这些研究方法均存在精度低、误差大等不足。
针对上述问题,本文采用湖北省武汉市某水位站的历史数据作为数据集,采用MATLAB软件选取不同结构参数的神经网络模型,对其进行分析,从而选择最优的网络结构建立时间序列神经网络模型。利用该模型对2020年5月29日至2021年8月28日的逐时水位进行预测,验证模型的有效性和准确性,达到对河流水位的精确预测。
2 时间序列神经网络
要对河流水位进行精确的预测,就必须找到一个最恰当的函数对历史数据进行拟合分析,寻找这个函数的方法就是建立一个时间序列模型[8]。
BP(Back Propagation)神经网络是一种按误差逆传播算法进行训练的多层前馈网络,也是目前应用最广泛的一种神经网络模型[9, 10],由输入层、输出层以及两者之间的隐含层三部分组成[11]。其特点为信号前向传播,而误差反向传播。信号经过逐层处理到达输出层时,发现结果未达到期望值,于是原路返回进行反向传播,同时对各层权重等值进行修正,调整误差,直至输出结果为期望值[12]。
BP算法计算流程如下:
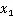
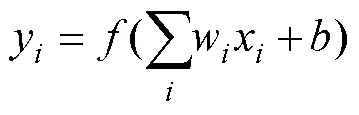
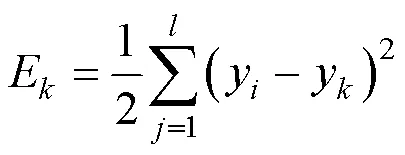
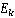
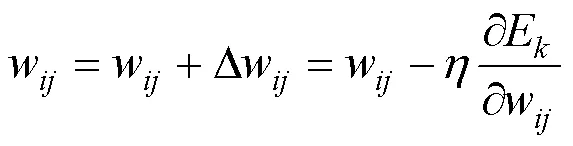
(4)设定迭代终止条件,当输出误差小于一定值或学习次数达到要求时,算法终止,输出结果。
假设神经网络隐含层的神经元数量为任意个数,其特性函数任意阶可导,则构建的3层BP神经网络模型可任意精度逼近任意连续函数[13]。因此选取合理的结构参数就能够利用神经网络推导出最优的非线性函数。
3 建立模型
3.1 数据集的来源
本文的数据来源于武汉市公共数据开放平台(http://data.wuhan.gov.cn/page/data/data_set_details.html?cataId=4d6ac7b12a024aad83fb5e4968e1eb5b),收集采用了位于湖北省武汉市某水位站2019年7月29日至2021年8月29日的逐时水位时间序列作为数据集。
3.2 生成样本集
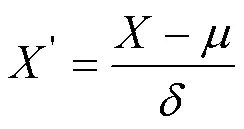
3.3 结构参数的设置
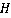
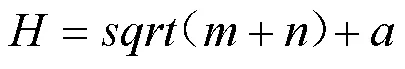
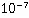
3.4 模型评价指标
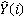
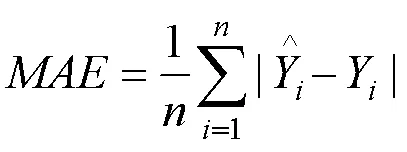
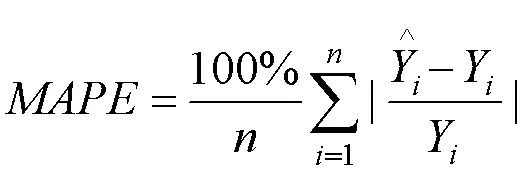
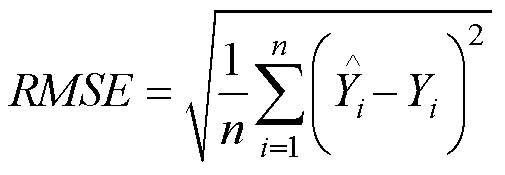
4 模型验证及结果分析
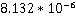
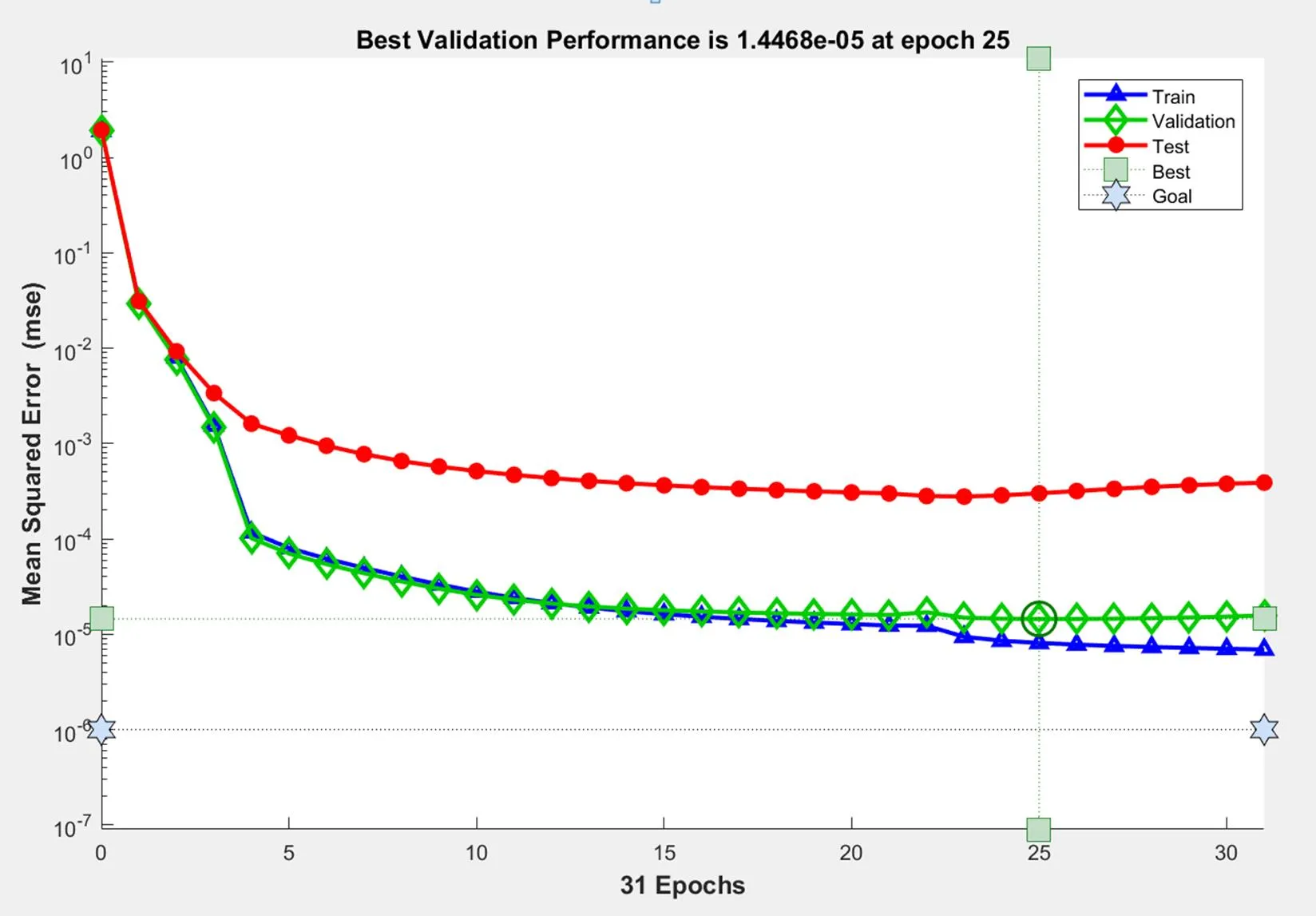
图1 训练曲线图
由于神经网络容易出现过拟合现象,因此,需要分别对训练集的预测值与真实值,验证集的预测值与真实值和测试集的预测值与真实值进行线性拟合,拟合结果如图2所示。训练集的拟合系数R=0.99998,极为接近1,说明此模型的训练效果极好,预测精度极高。验证集的拟合系数R=0.99997,测试集的拟合系数R=0.99941,同样极为接近1,说明该模型在测试集中同样具有极高的预测精度。对整个模型综合验证回归参数如图2所示,所得拟合系数R=0.99993,拟合效果极好。综上所述,该时间序列神经网络模型准确率高,具有良好的可行性。
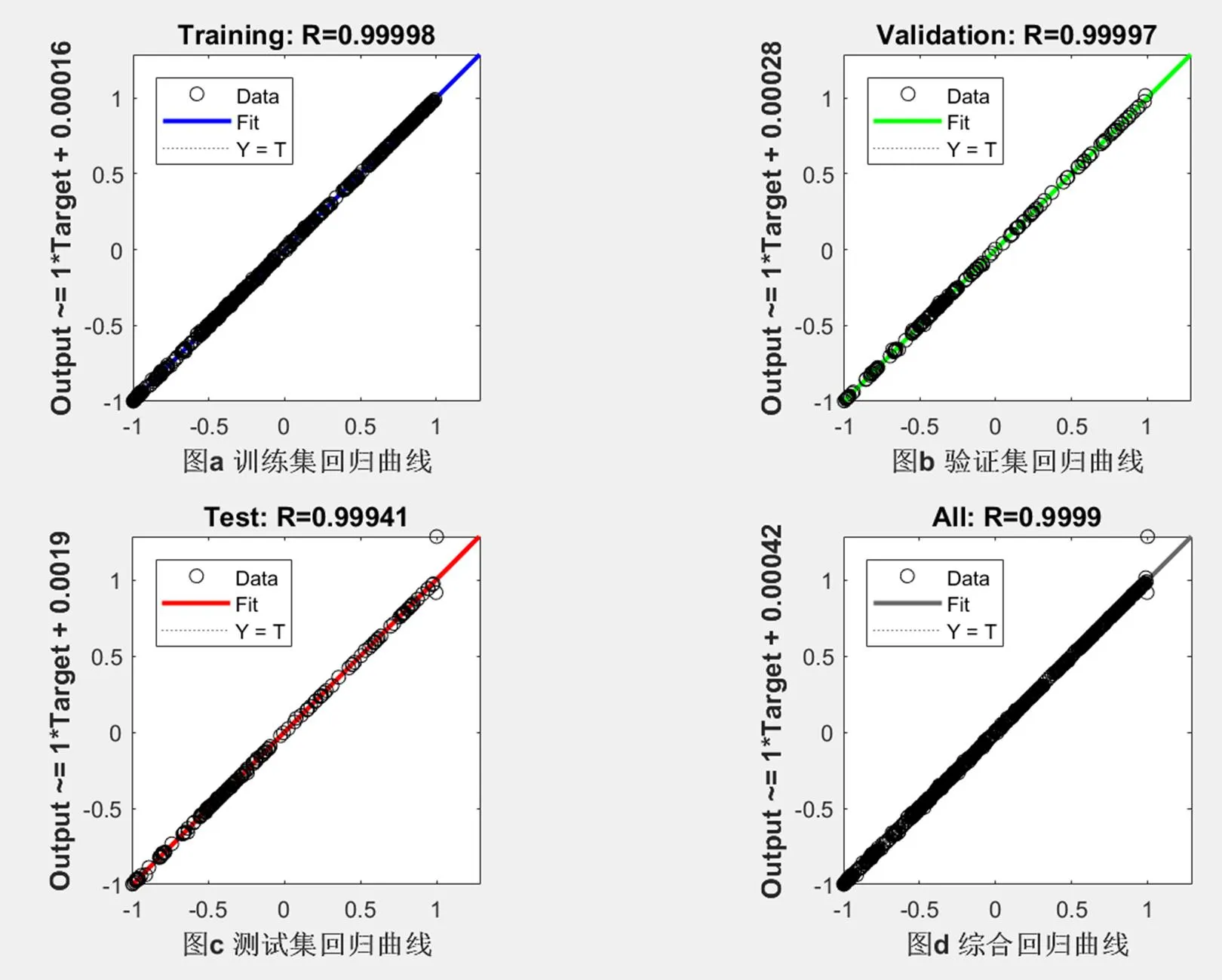
图2 训练集、验证集、测试集和综合验证的回归曲线
该时间序列神经网络模型对500个测试样本的检验对比结果如图3所示,预测值与真实值极为接近,离群点极少,预测精度极高。预测误差如图4所示,神经网络预测的水位值与真实水位值的误差绝对值绝大部分小于0.2,最大相对误差为0.3543,平均绝对误差0.00663,均方根误差0.081434,平均绝对百分比误差0.23785%,在水位达到极值附近预测值的误差波动相对较大,其他时刻误差极小,说明该时间序列神经网络模型预测精度极高,对河流水位的预测有着重要参考意义。
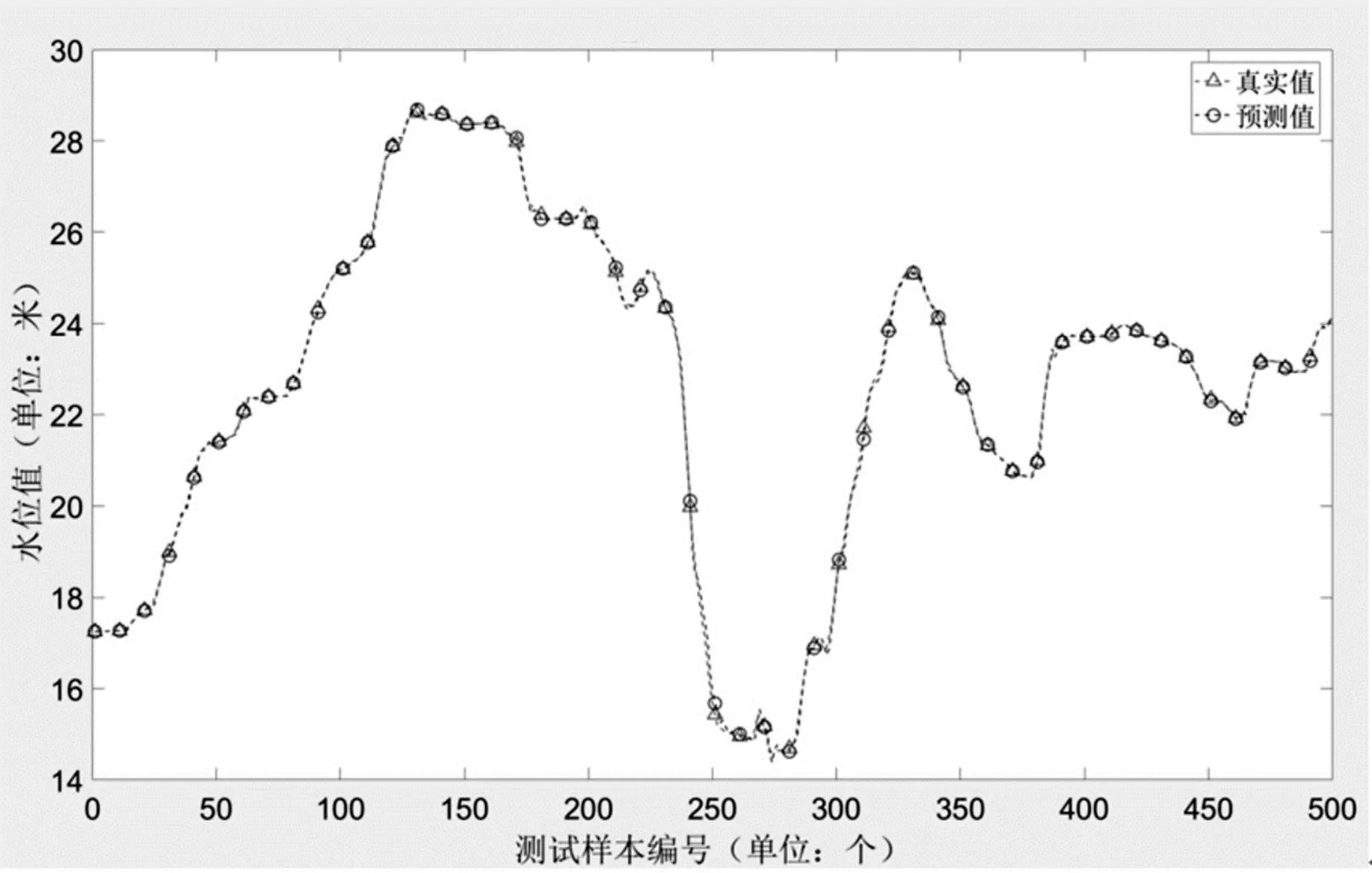
图3 测试集真实值和预测值的对比
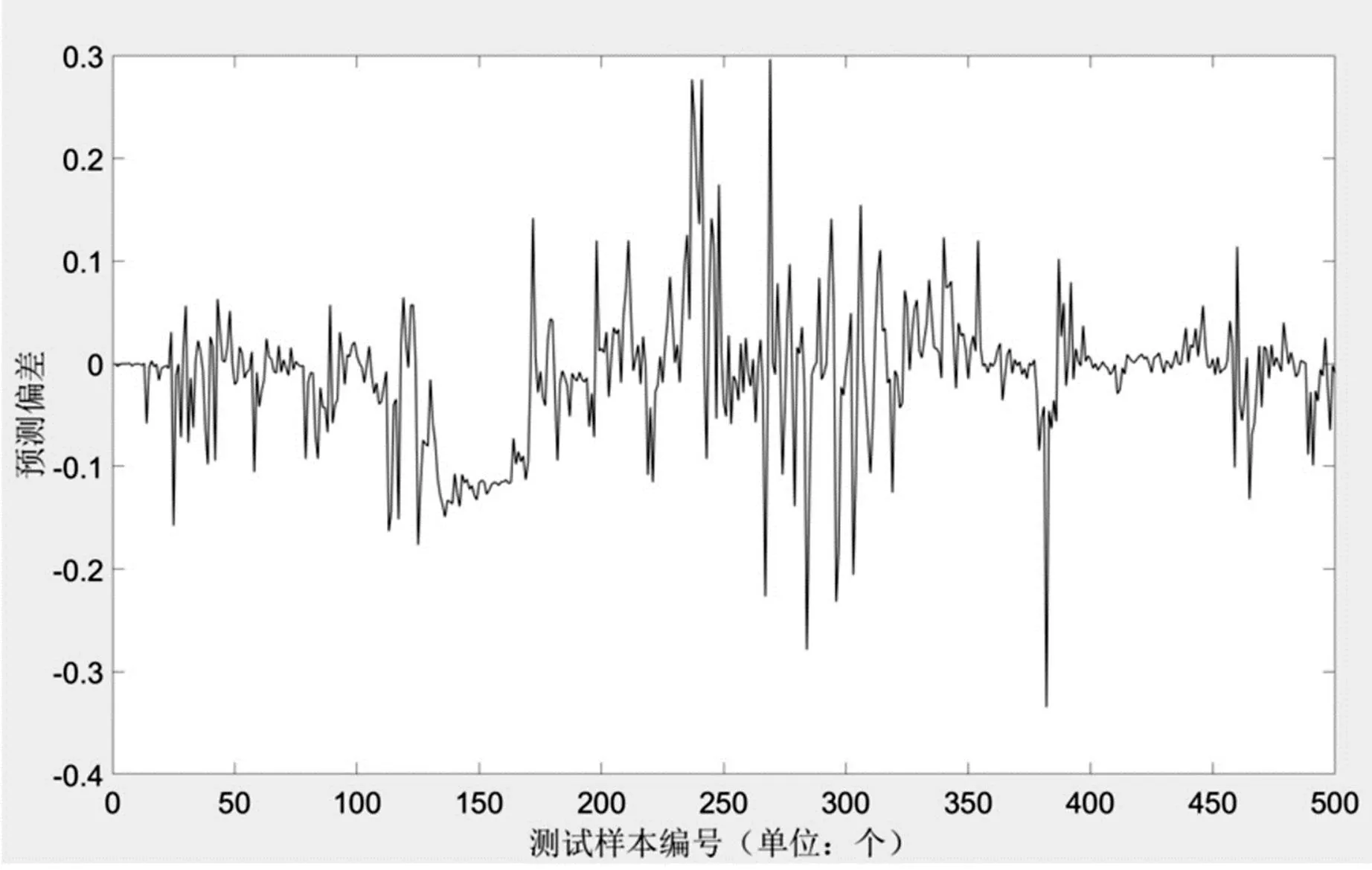
图4 测试集的预测误差
5 结语
本文采用了湖北省武汉市某水位站2019年7月29日至2021年8月29日的逐时水位时间序列作为数据集,使用MATLAB软件建立了一个基于时间序列神经网络的水位预测模型,该模型的平均绝对误差0.00663,均方根误差0.08143,平均绝对百分比误差0.23785%,精确预测了武汉某水位站2020年5月29日至2021年8月28日的逐时水位,能够为河流防汛预警工作和航道综合通行能力等方面提供参考。
[1] 周星妍,曾红玲,王遵娅,等. 2018年中国气候主要特征及主要天气气候事件[J]. 气象,2019, 45(04): 543- 552.
[2] 李莹,曾红玲,王国复,等. 2019年中国气候主要特征及主要天气气候事件[J]. 气象,2020, 46(04): 547-555.
[3] 代潭龙,王秋玲,王国复,等. 2020年中国气候主要特征及主要天气气候事件[J]. 气象, 2021, 47(04): 478- 487.
[4] 韩卓慧,闫长青. 基于PG-BP神经网络的流域洪涝预测及仿真[J]. 软件导刊,2021, 20(05): 50-55.
[5] 卞宁. 改进型灰色系统在航道水位预测中的应用[J]. 中国水运.航道科技,2018, (05): 75-80.
[6] 刘光星,李巧花. 基于粒子群算法的BP神经网络在地下水位预测中的研究[J]. 电子测试,2019, (07):51-52.
[7] 马辉,孙颍桃,肖艳,等. 基于灰色-BP神经网络组合模型的水位预测案例[J]. 人民黄河, 2016, 38(12):89-92
[8] 田铮. 时间序列的理论与方法[M]. 北京:高等教育出版社, 200l. 355-357.
[9] 钟颖, 汪秉文. 基于遗传算法的BP神经网络时间序列预测模型[J]. 系统工程与电子技术, 2002, (4): 9-11.
[10] 丛爽. 面向MATLAB工具箱的神经网络理论与应用[M].合肥: 中国科学技术大学出版社, 1998.
[11] 郑君里,杨行峻. 人工神经网络[M]. 北京:高等教育出版社,1992. 15-30.
[12] 王小川, 史峰, 郁磊,等.MATLAB神经网络43个案例分析[M]. 北京:北京航空航天大学出版社, 2013. 344-345.
[13] 黄俊,周申范,唐婉莹. TNT生化降解时间序列的人工神经网络预报模型[J]. 环境科学研究, 2000, (2): 3-5.
Based on Time Series Neural Network Prediction of River Water Level
LIU Da, LUO Wei-ping
(School of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan Hubei 430200, China)
In view of the frequent flood disasters and difficulties in the passage of river waterways in China every year, a high-precision water level prediction model based on time series neural network is constructed, which can effectively predict the water level of the river, and then it makes emergency treatment in time to reduce the loss of life and property. The model uses the hourly water level time series of a water level station in Wuhan City, Hubei Province from July 29, 2019 to May 28, 2020 as training samples for training, and the hourly water level time series from May 29, 2020 to August 28, 2021. The data of 500 samples composed of the time water level are tested as the test sample. The average absolute error between the predicted water level value and the real water level value of the model is 0.00663, the root mean square error is 0.08143, and the average absolute percentage error is 0.23785%. The prediction accuracy is extremely high and has strong practical application prospects.
BP neural network; time series; water level prediction
TP275
A
2095-414X(2022)04-0043-05
通讯作者:罗维平(1967-),女,教授,研究方向:检测技术与智能控制、信号与信息处理.

