基于Friis传输公式的RSSI测距模型研究
徐文染,陈燚涛
基于Friis传输公式的RSSI测距模型研究
徐文染,陈燚涛*
(武汉纺织大学 机械工程及自动化学院,湖北 武汉 430200)
基于弗里斯(Friis)传输模型,给出了一种基于RSSI的RFID阅读器与无源标签通信时的理论测距模型,并通过实验数据对标签进行标定,得到每个标签最终的测距模型,并与常用的对数阴影模型进行对比,实验结果表明,本文的模型有相对较高的测距精度。
室内定位;RFID;RSSI;测距模型
0 引言
随着物联网的飞速发展,越来越多的服务需要基于室内定位[1]。常见室内定位技术有磁导航、惯性导航、激光定位导航、蓝牙导航、超声波定位、RFID等[2]。其中RFID技术凭借非接触、非视距、时延短、高精度以及成本低等优点在室内定位系统中得到了广泛的应用[3]。利用RFID做室内定位的方法主要分为两大类[4]:基于测距法和基于非测距法。非测距的定位算法无需获取两节点间的距离或角度信息,只需根据被测目标当中的连通性来对距离进行推算,定位精度较于测距法而言较低。常用的测距方法包含信号到达时间(TOA)、信号到达时间差(TDOA)和信号接收强度(RSSI)[5]。其中RSSI测距算法难度较低,易于实现,不需要额外增加硬件设施,是大多数室内定位系统的首要选择[6]。RSSI测距定位的主要缺点在于传播信号易受环境干扰,导致信号强度产生不同程度的衰变,影响测距精度[7]。
为了解决此问题,已有诸多学者提出了相应的解决方法,其中一些改进方式集中在改善RSSI数据可靠度上面,如文献[8]~[11]所列,其中文献[8]采用粒子滤波模型对RSSI值进行处理以获得更为可靠的强度值。文献[9]采用了一种基于狄克逊检验法滤波RRSI的高斯牛顿定位算法,对观测信号进行高斯均值滤波剔除异常值。文献[10]提出基于RSSI高斯滤波的人工蜂群定位算法,采用高斯滤波对收集的RSSI值进行处理,保留精度较高的RSSI值。文献[11]提出一种混合滤波法。这些策略采用对测得RSSI值进行滤波处理的方法,并没有修正RSSI的测距模型,对测距精度的提升有限。还有一些改进策略集中在定位算法上面,如文献[12]提出先建立符合实际环境的基于RSSI-距离区间映射的数据库,再采用加权质心算法确定具体位置。文献[13]提出基于RSSI修正和集员法的节点定位算法,通过修正RSSI测距,利用集员法估计节点位置。文献[14]给出了一种室内的基于RSSI的加权四角质心定位法。这些策略理论上能在一定的程度上提高定位精度,但是其默认了RSSI测距是精确的,在实际室内环境中,由于信号的不稳定性,会导致测距精度的丢失,最终影响定位算法的准确性。
根据现有解决方案存在的问题,本文根据天线发射电磁波的特点以及电磁波在空间中传播的特性,利用发射功率密度与接收天线的有效接收面积的乘积来获取信号传播的理论模型。考虑到室内复杂环境造成的电磁波反射、散射、绕射等影响,在此理论模型的基础上添加一个室内修正函数并对每个标签进行标定,最终得到本文的信号能量传播模型。通过实验验证,本模型在室内测距中有较高的精度,相较于传统的对数正态阴影模型,测距精度有了较大提升。
1 RFID系统组成及RSSI原理
1.1 RFID系统组成
如图1所示。一套完整的RFID系统包括RFID阅读器、天线、RFID电子标签和电脑终端系统。RFID阅读器用来读取和修改标签所存储的信息,天线用来接收和发射电磁波信号,标签则负责储存特定的目标信息。工作时,标签通过阅读器发射的电磁辐射获得能量,获取到信息提取指令后,将自身存储的信息以电磁波的形式发送出去,阅读器获取到标签的信号时,除了能读取到标签自身存储的信息外,还会获得一个信号能量信息,最后根据能量的传播模型来确定阅读器与标签的距离。

图1 RFID工作原理
1.2 基于弗里斯(Friis)的无线信号传播模型
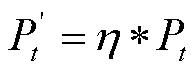
那么距离发射天线距离为R处的辐射功率密度为:
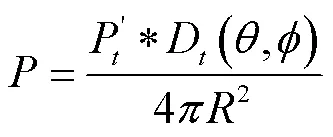
其中Dt为发射天线在方向(θ,φ)的方向系数,一般情况下,发射和接收天线均以最大增益方向对准。接收天线的接收功率Pr为:
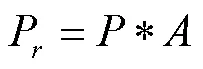
其中A为天线接收等效面积,与天线增益和波长有关。
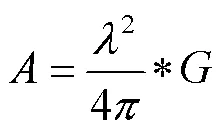
G为天线增益,与天线的方向系数相比,天线增益考虑了天线的能量转换效率。即:
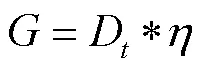
将(1)(2)(4)(5)式带入(3):
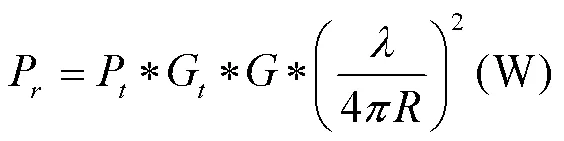
可将RFID阅读器与无源标签之间的通信过程看成是两段发射机与接收机的信号传递过程。如图2所示。第一段将RFID阅读器看成是发射机,标签为接收机。第二段,将标签看成是发射机,RFID阅读器作为接收机,将标签的接收功率作为发射机的输入功率,那么第二段接收机的接收功率则为RFID阅读器理论上最终获取的功率。式(6)计算出的Pr为第一段标签所接收到的功率。第二段则是将Pr作为发射天线的输入功率,得到接收机所得到的接收功率Py为:
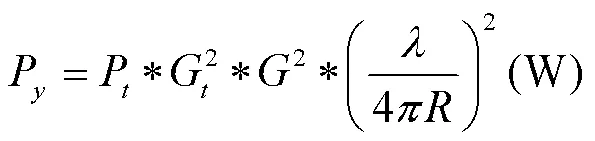
RFID实验设备测得的信号强度均是以dBm表示,故将(7)式单位转换为dBm,则变为:
HPLC分别检测脂质体制备前混合物与脂质体制备后超滤所收集的未包封药物,根据HPLC峰面积计算包封率=[(Wa-Ws)/Wa]×100%(Wa:初始投药量;Ws:上清液中含药量)。结果显示,脂质体制备前后HPLC结果图(见图3制备前,图4制备后滤液)三个峰依次为异烟肼、吡嗪酰胺及利福平,包封率分别为异烟肼90%、吡嗪酰胺37%及利福平88%,见图 3~4。
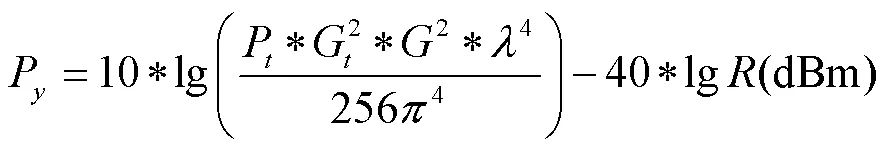
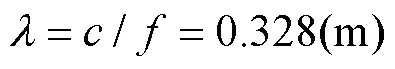
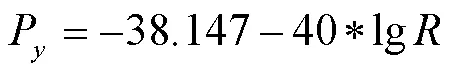
但是,电磁波在室内传播时,由于环境的复杂性,会产生反射、绕射和散射现象,会产生多径效应,会使电磁波能量的传播与理论信号传输模型产生一定的偏差。为了考虑复杂的室内环境的影响,在式(9)的理论传播模型基础上添加一个室内修正函数f(R),综合考虑到计算的复杂性与修正的准确度,将f(R)设定为一个与传播距离相关的二次多项式,最终通过实际的实验数据拟合出来。最终本文的信号能量传输模型为:
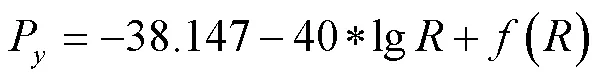
2 实验分析
2.1 RSSI测距实验
实验是在教学楼楼道中进行的。实验通过调整RFID阅读器与无源标签之间的距离,记录RFID阅读器接收的信号强度RSSI随着距离R变化的关系。使用的RFID设备是四川睿频科技有限公司的RP26模块接口板,支持ISO18000-6C与EPC C1G2协议,功耗低、体积小。工作温度为-25℃~+80℃,发射功率可在-9dBm~26dBm之间自由调整,工作频率在840MHz~960MHz之间,通过USB接口与上位机进行通讯。阅读器天线为圆极化天线,增益为9dBi。实验中,将RFID阅读器发射功率固定为26dBm,设置在915MHz频率下工作。
实验过程中将阅读器的天线固定,然后通过移动标签的位置来调整阅读器与标签之间的距离,在0.3m~4.2m的范围,每隔0.3m记录5组数据。为了减小偶然因素对实验数据造成影响,取五组数据的平均值作为当前标签在当前距离的RSSI值。记录10个标签的数据,最后取10个标签在同一距离处的均值作为最终的实验数据,得到的实验数据如(图3)。
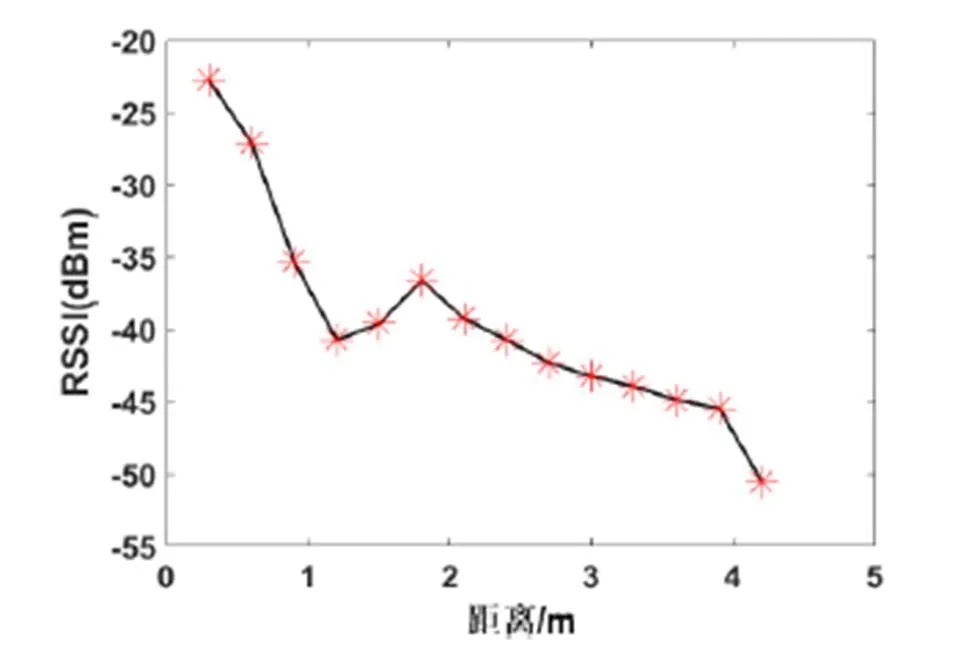
图3 距离与信号强度数据
根据实验数据,通过MATLAB对(10)式进行拟合分析,拟合得到修正函数f(R )的参数后,就得到了本文经过修正后的信号传播模型:
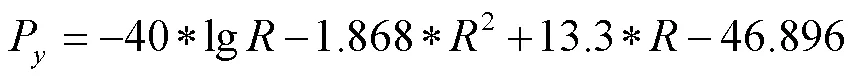
拟合后的图形如图4(a)所示:从图可以看出,随着距离的增加,RSSI逐渐递减,且变化的趋势逐渐平缓。在1.5m之前,RSSI随着距离的增加衰减较快,此后逐渐平稳。从数据的贴合度来看本文信号传输模型有一定的准确性。
2.2 标签标定
虽然实验使用的都是同种型号的标签,但是由于制造误差,每个标签的测量数据都不尽相同,故单一的信号传输模型难以描述所有标签的RSSI与距离的关系,因此需要对每个标签进行标定,针对性的提高测距模型的定位精度。标定完成后,对于每个标签都有其单独的信号传输模型。对标签进行标定时,取几组标签的实验数据,综合考虑计算复杂度与精度在本文模型的基础上添加一次项标定函数。本文对1~3号标签进行标定,标签数据如表1:

表1 标签标定数据
标定之后得到的三个标签的信号传输模型分别为:
标签1:
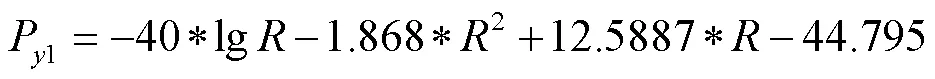
标签2:
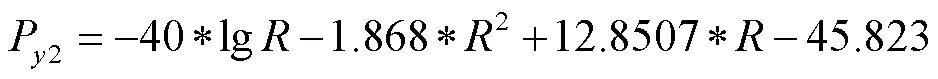
标签3:
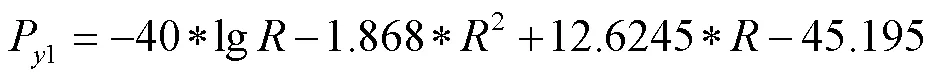
与标定模型对应的图形如图4(b)、4(c)、4(d)。
从图4可以看出,经过标定后的信号传输模型与标签的数据更加贴合。
3 模型验证
为了测试本文提出的传输模型的优劣,将本文标定后的信号传输模型与经典的对数正态阴影模型进行测距精度对比。对数正态阴影模型是目前利用RSSI进行室内定位中使用最多的模型。无线信号在复杂的室内传播时,由于反射、散射、衍射等各种因素的叠加影响。在传播过程中的能量损耗较大。相对于自由空间衰减模型、地面反射模型及对数路径损耗模型,对数正态阴影模型考虑了室内传播过程中路径损耗问题[15],弥补了对数距离损耗模型没有考虑测距值变化的情况[16],该模型的信号传输公式如下:
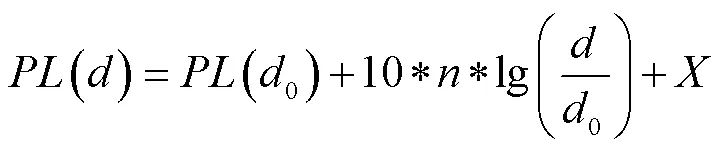
式中,各参数的含义为:d接收机和发射机之间的距离;d0为基准距离(m),通常取1m;PL(d)表示接收机和发射机距离为d时接收机所接收到的信号功率;PL(d0)表示基为d0时,所接收的信号功率;X为一高斯随机变量,其均值为0;n为信号衰减因子,与具体的室内环境有关,范围一般为2~4。在实际应用中,简化对数正态阴影模型[17]为:W
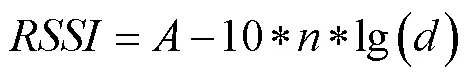
根据实验数据,利用MATLAB将(16)式进行拟合分析,得到的对数正态阴影模型为:
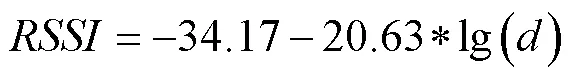
得到的函数图形如图5(a)所示,将其与标签1、2、3的实验数据进行比较,分别得到图5(b)、5(c)、5(d)所示图形。
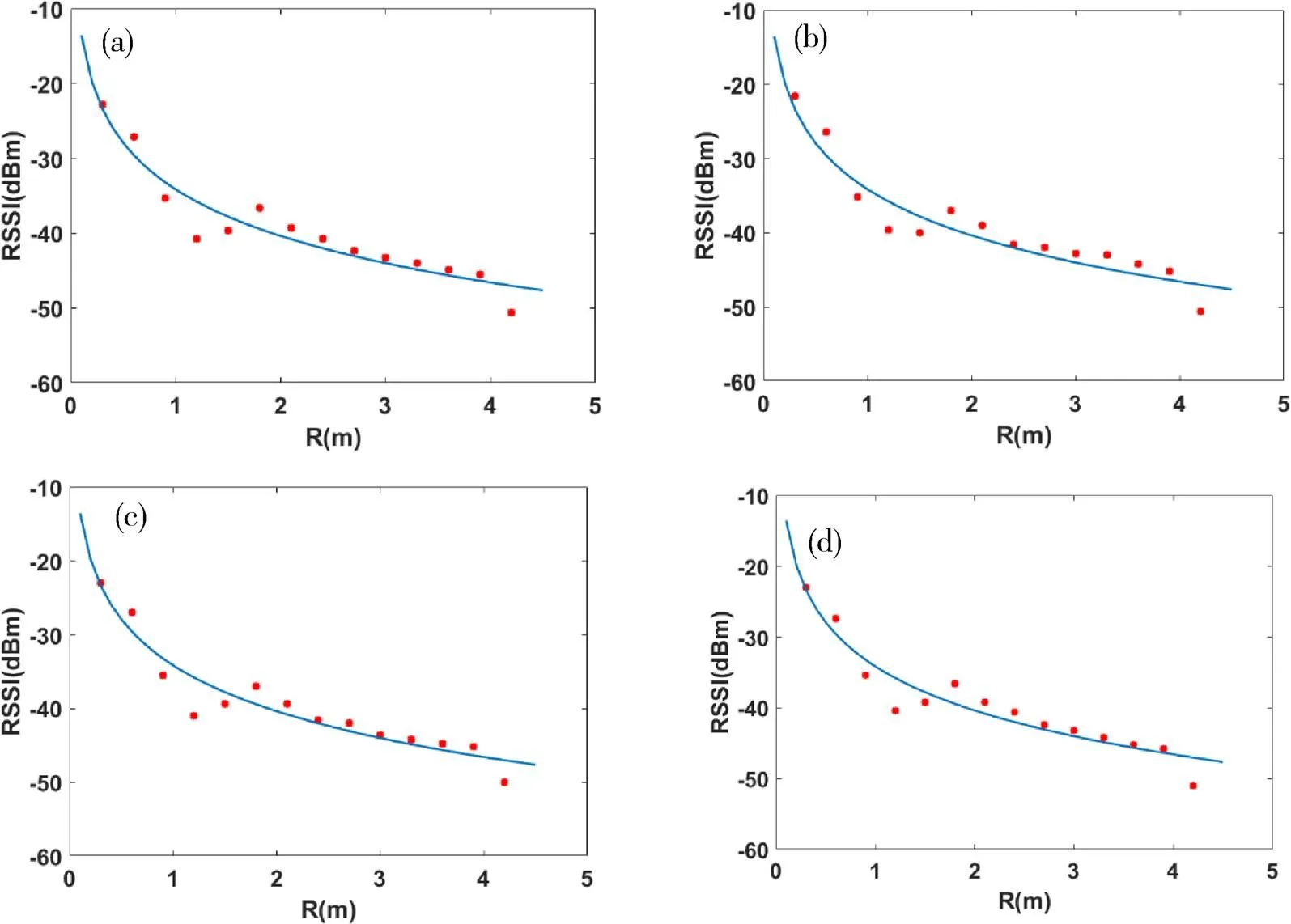
图5 对数正态阴影模型
图4(a)和图5(a)分别是本文修正模型和对数正态阴影模型拟合出的图形。从图中可以看出本文模型与对数正态阴影模型均能较好的表示RSSI与距离d的变化趋势,通过观察图4(b、c、d)和图5(b、c、d)可看出两种模型在2.1m~4.2m处与实验数据的贴合程度最高,故将2.1m~4.2m作为本文的数据有效区间。表2给出了标签1~3在两种模型的有效区间中的平均误差及均方差,由表2中的结果可见,本文提出的模型无论是测距的平均误差还是均方差都比对数正态阴影模型的误差要小,测距精度有了很大的提高。因此可将本文标定后的信号传播模型应用于RSSI测距工作。
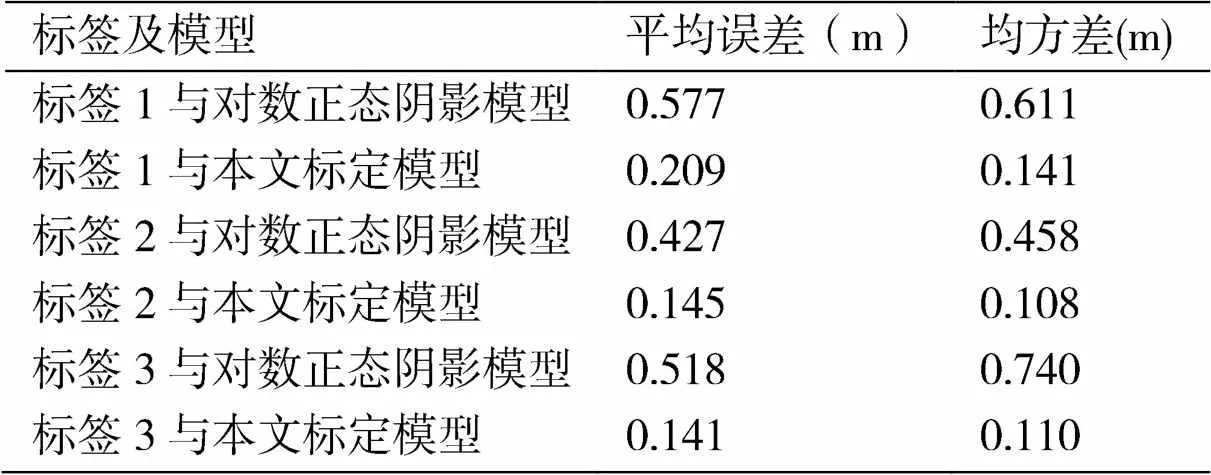
表2 两种模型误差度对比
4 结语
本文在弗里斯(Friis)传输公式的理论基础下,通过理论分析,推导出了RFID阅读器与无源标签进行通信时电磁信号在空间中的理论传播模型,为了将室内影响因素考虑进模型,在理论模型的基础上添加了一个室内修正函数。通过实验,记录了在室内中RSSI与距离d的实验数据,然后通过MATLAB对模型进行拟合,得到本文的传输模型,利用此模型与标签的数据对标签进行标定,最后通过与对数正态阴影模型相比较,通过实验数据看出,本文的模型能大幅提高测距精度。
[1] 刘晨. 基于角度补偿的RSSI测距系统设计与实现[D]. 南京:东南大学, 2019.
[2] 邓照群. 基于RFID的室内定位技术研究[D]. 长春:长春理工大学, 2017.
[3] Sarkka S. Phase-Based UHF RFID Tracking With Nonlinear Kalman Filtering and Smoothing[J]. IEEE Sensors Journal, 2012, 12(5): 904-910.
[4] 吴王润. 基于改进LANDMARC 算法的RFID室内定位系统研究与实现[D]. 长沙:中南大学, 2014.
[5] 邹东尧, 陈鹏伟, 刘宽. 一种改进的RSSI测距定位算法[J]. 电讯技术, 2019, 59(10): 1191-1196.
[6] 蓝芳萍, 张文锦, 殷旭东. 基于ZigBee和RSSI测距算法的室内定位系统设计[J]. 软件导刊, 2018, 17(2): 110- 113.
[7] 石琴琴, 徐强, 张建平, 等. 基于RSSI测距的室内目标定位方法[J]. 电子测量与仪器学报, 2018, 32(2): 86-91.
[8] 赵珊, 付敬奇. 基于粒子滤波模型的RSSI测距优化研究[J]. 电子测量技术, 2016, 39(03): 122-126.
[9] 王建强, 代阳, 雷倩芳. 狄克逊检验法滤波RSSI的室内定位算法[J]. 传感技术学报, 2021, 34(1): 118-123.
[10] 单好民, 陈才学. 基于RSSI高斯滤波的人工蜂群定位算法[J]. 传感技术学报, 2021, 34(7): 979-983.
[11] 郑志浩, 李雷, 李国逢, 等. 一种基于RSSI混合滤波和分段式拟合测距模型的室内定位方法[A]//第十二届中国卫星导航年会论文集——S09 用户终端技术[C]. 2021. 133-141.
[12] 沈田, 温斌. 基于RSSI-距离区间映射的加权质心定位算法[J]. 电子测量技术, 2015, 38(05): 42-44+61.
[13] 房亚群, 安进. 基于RSSI测距修正和集员法节点定位算法[J]. 计算机工程与设计, 2018, 39(2): 463-467.
[14] 余泳. RFID信号强度和惯性测量室内融合定位[D]. 合肥:安徽理工大学, 2020.
[15] 杨丽. 基于RSSI的RFID标签定位算法研究[D]. 南京:东南大学, 2019.
[16] 周二林, 王冠凌. 基于RSSI测距的室内定位研究[J]. 重庆理工大学学报(自然科学), 2014, 28(09): 98-101+121.
[17] Brooks R R, Ramanathan P, Sayees A M. Distributed Target Classification and Tracking in Senson Networks[A].In Proceeding of the IEEE[C]. Cambridge: Cambridge University Press, 2003. 271-310.
Research on RSSI Ranging Model based on Friis Transmission Formula
XU Wen-ran, CHEN Yi-tao
(College of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan Hubei 430200, China)
Based on Friis transmission model, a theoretical ranging model for RFID reader communication with passive tags based on RSSI is proposed. The final ranging model of each label is obtained by calibrating the label with experimental data, and compared with the commonly used logarithmic shadow model. The experimental results show that the model in this paper has relatively high ranging accuracy.
indoor positioning; RFID; RSSI; ranging model
TP273
A
2095-414X(2022)04-0038-05
通讯作者:陈燚涛(1972-),男,教授,研究生导师,研究方向:基于RF1D的室内定位.

