某机型消音板等效简化及其特性分析

武东旭，林金保

(太原科技大学 应用科学学院，太原 030024)

普惠公司曾在2017年对于LPT3级叶片断裂事件的一份调查中指出，异物打伤是造成LPT3级叶片断裂的直接原因，即发动机气流通道上游的部件脱落打伤下游的LPT叶片[1]。飞机高速飞行或飞行状态发生改变时，消音板表面空气动力与消音板自身弹性作用下保持原来形态的相互作用，促使消音板振动，发生脱胶、分层，一些小块甚至整块材料飞脱掉入进气道之后贴在OVG(出口导向叶片)上，造成发动机喘振[2]。

乔海涛对飞机发动机进气道口消音蜂窝结构的制备工艺和降噪效果进行了分析[3]。侯鹏对声衬(消音板组合件)的结构形式、装配位置进行了介绍[4]。张丽娜对蜂窝夹层结构消音板进行了压缩试验研究，建立了蜂窝结构消音板的压缩应力—应变曲线[5]。目前，对于蜂窝芯子的等效模型简化理论已经比较成熟[6]，多孔面板的动力学等效也有研究人员进行探索[7]，而针对飞机进气道消音板的动力学分析比较少。了解结构的振动特性是结构优化设计的基础，因此，对于飞机进气道消音板的振动特性即模态分析是十分有必要的。本文简单介绍了蜂窝芯、多孔面板的简化方法，选取合适模型针对某机型消音板主要结构即多孔薄板、蜂窝夹芯分别进行简化，最后对简化之后的消音板模型进行动力特性分析并给出优化建议。

1 某机型消音板结构

某机型进气道消音板由三块独立的曲面消音板拼接成筒形铺设在发动机进气道，拼接缝分别位于两点钟、六点钟、十一点钟，每块消音板的结构从内到外构成依次为2024-T3铝合金多孔面板、内层5052铝合金蜂窝芯、声学隔膜、外层5052铝合金蜂窝芯、2024-T3铝合金实体背板，这五部分由胶接的方式组成一个整体刚性结构，其中多孔面板上分布着大量的声学微孔，在每6.45 cm2面积上冲出24个直径为1.96 mm的孔，结构如图1所示。

图1 进气道消音板结构Fig.1 Structure of inlet cowl inner barrel acoustic panel

2 消音板模型简化

2.1 蜂窝芯简化

蜂窝夹层结构是一种复杂的结构形式，具有比强度高、质量轻、比刚度大、隔振隔热性能优越等优点，被广泛应用于航空航天领域[8]。目前，三明治夹芯板法、Hoff等刚度法、改进的Allen法是最常用的蜂窝夹层板等效简化方法。在工程实际应用中，按照尺寸比例可将板结构分为薄板(厚度/边长<0.01)、中厚板(0.01<厚度/边长<0.1)和厚板(厚度/边长>0.1)，本文所研究机型进气道消音板(厚度/边长=0.071)属于中厚板。陈昊[9]采用数值模拟与实验相结合的方法研究了以上三种等效方法对于不同厚度蜂窝夹层板的适用性，对于蜂窝夹层薄板，采用三种等效建模方法获得的分析结果均具有较高的准确性，与精细有限元模型的计算结果相比，误差均小于5%，与试验结果相比，误差均小于 4%.对于蜂窝夹层中厚板和厚板，Hoff 等刚度法以及改进Allen 法误差过大，其适用性已经变差，而三明治夹芯板法仍然具有较高的准确性，如图2所示。本文采取三明治夹芯板法对于该机型进气道消音板进行等效简化。

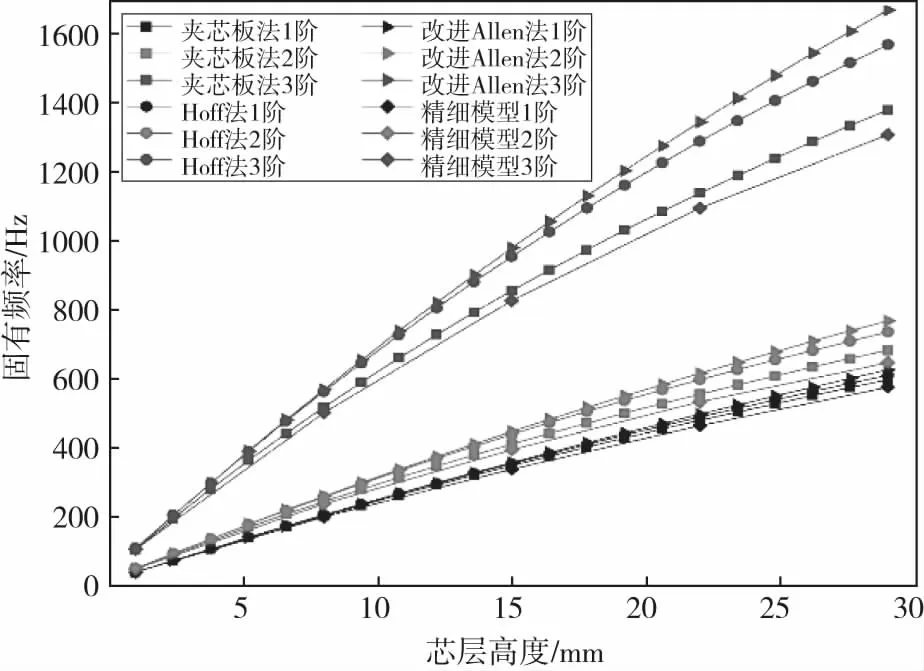
图2 三种等效方法与精细模型求解结果比较[9]Fig.2 Three equivalent method comparing with the refined model

三明治夹心板法是由Gibson理论衍生出的，采用 Kirchhoff板理论建立了面板的分析模型，采用均质正交异性材料本构模型作为芯层材料的本构模型，使蜂窝芯层等效为均质的厚度不变的正交异性层，即蜂窝芯子等效厚度与原厚度一致。相对于 Hoff 等刚度法和改进 Allen法，三明治夹芯板法考虑了更多的建模细节，尤其更深入的考虑了芯层不同方向的剪切刚度，因此更适用于分析蜂窝夹层中厚板和厚板。三明治夹芯板法将上下面板和芯层分开进行建模，重点在于计算蜂窝芯层的等效材料参数。由于该机型消音板内两层蜂窝芯与声学隔膜是胶接在一起的刚性体，且声学隔膜的厚度极小，所以忽略声学隔膜将两层蜂窝芯视为一个整体的蜂窝结构进行简化，即图3所示蜂窝夹层板示意图，其中H为蜂窝夹层板总厚度，h为两层蜂窝芯的高度之和，t为面板厚度，δ为蜂窝胞元的壁厚，l为六边形蜂窝外接圆半径，该机型蜂窝夹心层的具体尺寸见表1，由于该机用消音板蜂窝芯为正六边形结构，所以本文仅给出三明治夹心法简化正六边形蜂窝芯的等效材料参数计算公式(1)如下[10]：

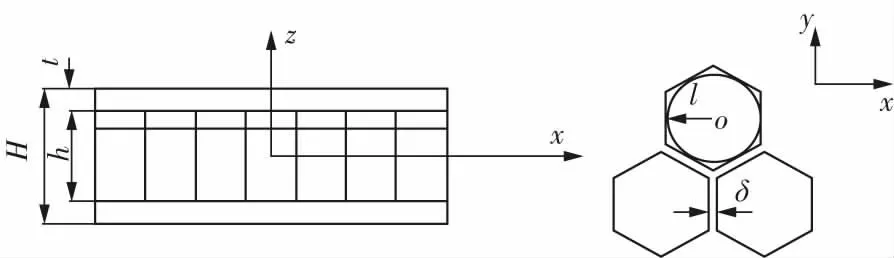
图3 蜂窝夹层板示意图Fig.3 Schematic diagram of honeycomb sandwich structure

表1 蜂窝夹芯层几何参数

(1)

式(1)中ρs、ES、GS、μs分别为蜂窝芯材料的密度、弹性模量、剪切模量、泊松比；Ecx、Ecy、Ecz为三个方向的等效弹性模量；Gcxy、Gcxz、Gcyz为三个坐标面内的等效剪切模量；ρc为等效密度；μc为等效泊松比；式中γ为修正系数，理论值取1，一般取0.4～0.6，本文取0.5.计算得到蜂窝芯等效材料参数见表2.

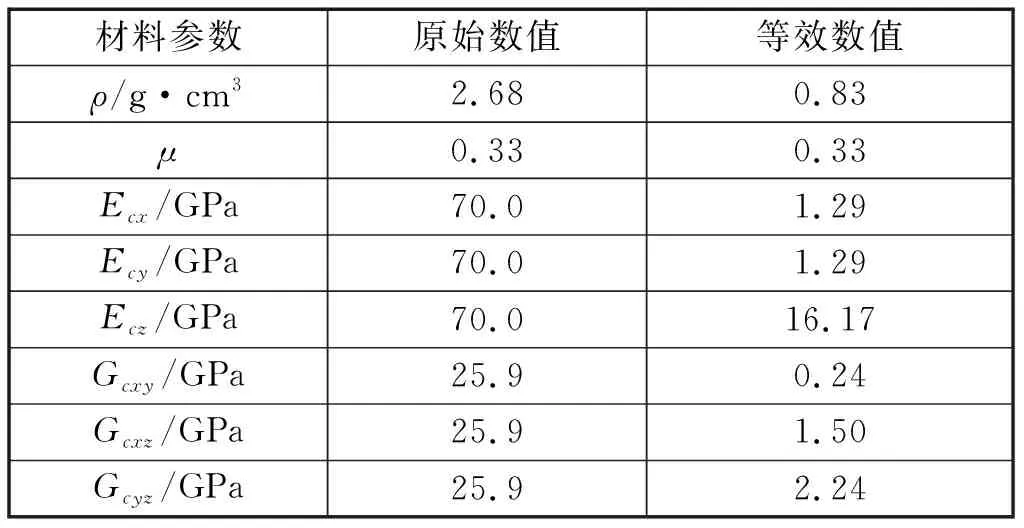
表2 蜂窝芯等效材料参数Tab.2 Honeycomb equivalent material parameters

2.2 表层多孔面板的简化

目前，对于多孔板的动力学等效模型研究较少，Myung Jo Jhung[11]针对多孔板提出一种简化方法，由图4可知，使用该方法得到的等效模型计算结果与精细模型计算结果十分接近。由于动力学特性只和质量、刚度相关，设定目的等效模型的轮廓尺寸、密度均与多孔板一致，则只需找到使得目的等效模型与多孔板原始模型动力等效的弹性模量关系即可满足等效简化，通过有限元数值模拟的方法将目的等效模型计算结果与实际模型计算结果进行横向对比，处理数据后得到等效模型与实际模型弹性模量的关系式(2)、(3)，分别是冲孔分布为三角形和正方形的多孔板等效弹性模量计算公式：

图4 实际模型与等效模型固有频率结果比较[11]Fig.4 Comparison of results between the actual and equivalent model[11]

2.2733η3-1.1471η4

(2)

2.4894η3-1.3499η4

(3)

其中E为多孔板材料的弹性模量，Eeq为等效实体板的弹性模量，η为两相邻冲孔最近距离与圆心距离的比值，使用公式(3)计算得到消音板表面多孔板等效弹性模量为68.01 GPa.

3 消音板的模态分析

结构的振动特性是结构动力分析优化设计的基础，分析其它动力学问题的首要步骤需要进行模态分析[12]。根据上文等效材料参数在有限元软件ANSYS中建模，根据消音板实际工况对其进行约束后选取Lanczos法对消音板等效模型进行模态分析，图5为前五阶模态振型图，消音板前五阶仿真模态频率及振型描述如表3所示。

图5 消音板模态振型云图Fig.5 Acoustic panel modal vibration contour

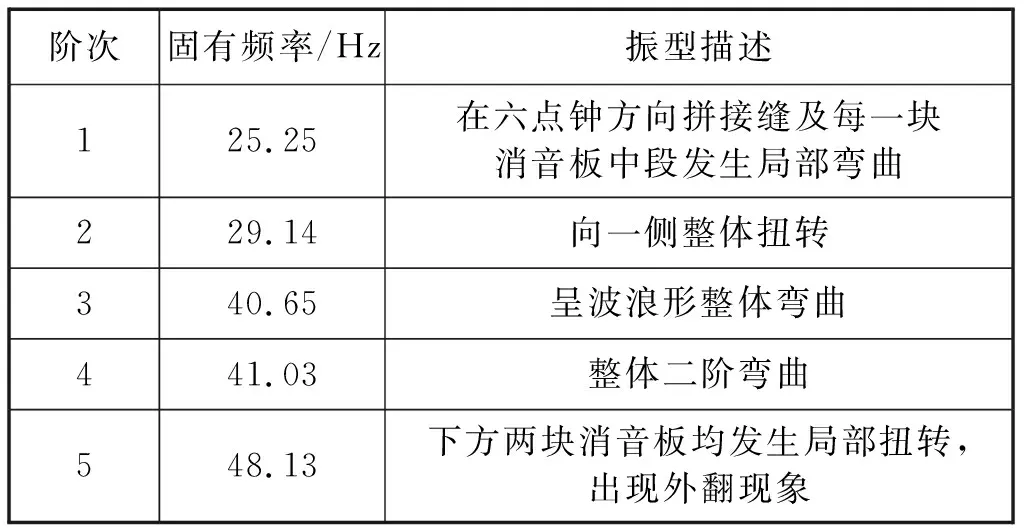
表3 消音板前五阶模态频率及振型描述

结合图5和表3可以看出，该机型消音板第一阶固有频率为25.25 Hz，主要在六点钟方向的拼接缝以及每块消音板的中段位置发生局部弯曲；第二阶固有频率为29.14 Hz，是消音板整体一阶扭转模态，其中，振动幅度大的部位在下方两块消音板的中段位置；第三阶固有频率为40.65 Hz，是整车的一阶弯曲模态，消音板整体发生对称的弯曲振动，其中两点钟和十一点钟位置的拼接缝以及下方两块消音板的中间部位振动幅度最大；第四阶固有频率为41.03 Hz，消音板整体发生二阶弯曲模态，振型不再对称，振动幅度最大的位置离开拼接缝处，向消音板中间移动；第五阶固有频率为 48.13 Hz，模态振型为局部模态，下方两块消音板发生局部扭转，出现侧翻现象。

已知涡扇航空发动机的固有频率在150 Hz左右[13]，而此消音板的前五阶固有频率均在50 Hz以下，远低于发动机的一阶固有频率，可有效避免与发动机共振现象的发生。通过模态振型图5可知，该机型进气道消音板的低阶模态振型大部分属于整体模态振型即整体弯曲和扭转。特殊情况下，可能因为消音板局部主要是拼接缝处刚度偏低，在低频范围内也存在局部振型与整体模态振型一起出现。由消音板前五阶振型云图可知，该机型消音板的六点钟方向拼接缝是该消音板结构的最薄弱位置，需进行结构优化。

4 结论

本文通过理论分析和有限元仿真相结合的方式对某机型飞机进气道消音板主要部件，即表面多孔板和蜂窝芯分别进行动力学等效简化，得到各自等效弹性模量、等效密度，并对其进行了模态分析，提取了前五阶固有频率与模态振型，分析后得到以下结论：

(1)该消音板前五阶固有频率均在50 Hz以内，远低于发动机的一阶固有频率，不会有共振现象发生，可在安全性能的前提下发挥消音隔振的作用。

(2)该机型消音板前五阶振型基本属于整体振型，满足结构可靠性需求，但同时也伴随局部振型，需要对六点钟拼接缝处进行加强，进一步提高结构安全性。

本文的研究方法对于飞机进气道消音板及其他面板为多孔板的蜂窝夹层结构的动力学分析具有一定的指导意义。