乘用车轮毂性能试验仿真方法综述

孙 娜，孙华文，张振伟，冯 源，张士岩，范晓文

（1.天河超级计算淮海分中心，山东 临沂 510623； 2.临沂科技职业学院，山东 临沂 276000）

1 前言

乘用车轮毂是整车的重要组成部件、功能部件及安全部件，在乘用车行驶过程中，轮毂会承受各种动载荷和冲击载荷，其断裂会对车内乘客带来极大的生命危险。因此，在轮毂设计阶段，需严格保证其使用寿命及结构强度满足国标试验要求。轮毂的国标性能试验主要包括轮毂动态弯曲疲劳试验、径向载荷疲劳试验及13°冲击试验三种，国内外均对三种试验做出了详细的技术要求，可充分保证轮毂在乘用车行驶过程中不会因外部循环动态载荷或冲击载荷而发生疲劳断裂或强度断裂。

对于三种轮毂性能国标试验，许多传统生产轮毂的企业，其试验人员仅依靠试验室实际试验来检验轮毂是否合格，导致轮毂研发周期长、成本高，难以适应乘用车行业快速的发展需求。随着有限元方法和仿真技术的日渐成熟，越来越多的轮毂研发工程师运用有限元分析软件对轮毂进行有限元建模、应力应变分析及疲劳寿命预测，并通过与轮毂试验结果对比，验证了仿真分析结果的可靠性。多年来，国内外研究人员通过有限元仿真分析方法，快速的预测轮毂在三种国标试验工况下的作业性能，进而预先对轮毂进行优化设计，极大缩短了轮毂研发周期，降低了研发成本。

综上，本文通过简述轮毂动态弯曲疲劳试验、径向载荷疲劳试验及13°冲击试验仿真方法的研究进展，对轮毂三种性能仿真试验的前处理方法进行总结，为提高轮毂性能试验仿真结果的准确性提供参考。

2 轮毂基本结构及性能要求

轮毂，也称轮圈，主要由轮辋和轮辐两部分组成，其余结构还包括气门孔、轮缘、槽底、偏距与胎座等。轮辋用于支撑轮胎并承受轮胎气压和径向作用力，轮辐用于保护轮圈和加强轮毂强度，气门孔用于伸出轮胎气门，轮缘用于支撑轮胎并承受轮胎侧向力，槽底用于装卸轮胎，偏距用于提高整车制动稳定性，胎座用于轮胎转弯横向力和防止轮胎从轮圈中脱出。

轮毂通过螺栓与乘用车传动轴连接，发挥承重、牵引及缓冲等作用，主要承受整车的重力、车轮转弯的扭转力矩及来自外界的冲击力。随着汽车行业对轻量化、高速化要求的不断提升，轮毂在保证轻量的同时，还需具备足够的刚度、强度及抗疲劳损伤性能。因此，轮毂应满足国标中所设定的弯曲疲劳寿命、径向载荷疲劳寿命及抗冲击强度要求。

3 铝合金轮毂性能试验仿真方法

3.1 动态弯曲疲劳试验

轮毂动态弯曲疲劳试验用于模拟轮毂在乘用车行驶过程中因受弯曲力矩而发生疲劳失效的场景，其试验方法如图2所示，使用螺栓将轮毂与载荷施加杆连接，通过夹具将车轮轮辋固定在试验台上，试验时在载荷施加杆底端施加按固定频率旋转的弯矩。

图2 动态弯曲疲劳试验加载装置示意图

试验中，施加在加载杆上的弯矩值为

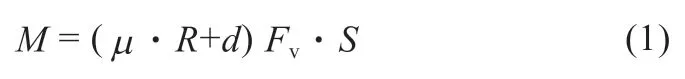
式中，μ为乘用车轮胎与公路间的摩擦系数；R为轮胎静负荷半径；d为车轮的内偏距或外偏距；F为车轮最大额定负荷；S为强化试验系数。其中，μ和S的取值见表1。

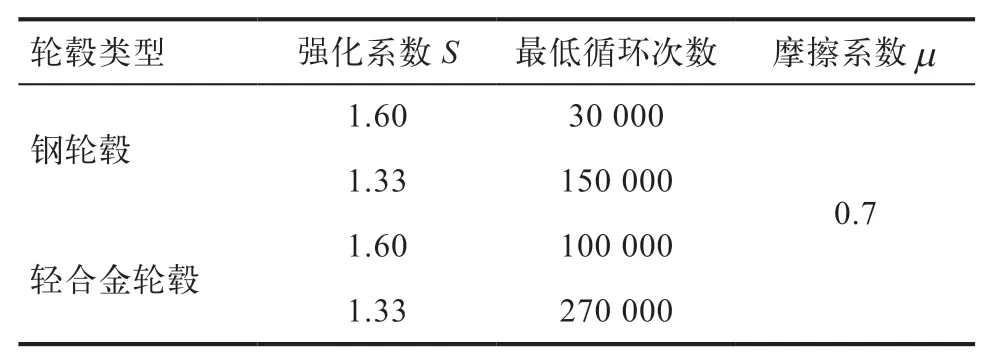
表1 轮毂动态弯曲疲劳试验要求

20世纪60年代，国内外研究者用“有限元法”开展了大量轮毂动态弯曲疲劳试验仿真研究工作。为研究各仿真模型的计算结果差异，文献[13]考虑了螺栓预紧力及轮毂与加载力臂材料不同对模拟试验的影响，建立了3种轮毂弯曲试验分析模型：①轮毂及加载力臂一体且材料相同的线弹性模型；②轮毂及加载力臂材料不同的线弹性模型；③考虑螺栓预紧力与接触关系的非线性模型，通过对比仿真结果与试验结果，模型1、2适用于易在轮辐处发生疲劳破坏的轮毂的分析，而模型3适用于易在法兰盘螺栓孔处发生破坏的轮毂的分析，且模型3最接近实际试验结果。

文献[7, 14-25]建立了包含轮毂、加载力臂、加载盘及螺栓在内的有限元模型，如图3所示，对各元件分别赋予了材料特性，建立了各元件间的装配及接触关系，约束了轮辋与夹具接触位置节点的6个自由度，在加载力臂远端施加了试验扭矩，得到了轮毂的应力云图结果。

图3 轮毂动态弯曲疲劳试验有限元模型

其中，文献[14-17]在加载力臂远端每隔一定角度θ依次加载了数个方向的垂直于加载力臂的静载荷，如图4所示，以模拟试验中载荷的周期变化，得到了轮毂的最大应力结果。

图4 弯曲载荷加载角示意图

文献[7,17]将轮毂上的装饰槽、圆角及气门孔等特征删除，以节省计算时间。文献[7,14-21]将轮毂静力分析结果带入材料S-N疲劳寿命曲线，预测了轮毂的动态弯曲疲劳寿命。文献[21-22]在轮辋和轮辐相连处添加了点焊缝模型，以更真实地模拟轮毂结构。文献[23]将加载力臂、加载盘及螺栓合并为一体，与轮毂建立装配及接触关系来减少接触对数量以使计算易于收敛，基于静力分析结果，使用软件ANSYS workbench中Fatigue疲劳分析模块预测了轮毂疲劳寿命。

为进一步简化仿真模型，加快计算速度，文献[26]仅建立了轮毂弯曲试验简化模型，在轮毂下轮缘处施加全自由度约束，将轮毂法兰螺栓孔与参考（RP）点耦合，在参考点上施加垂直于轮毂轴线方向的载荷，如图5所示，通过改变参考点载荷的方向来等效实际试验中的载荷变化，得到了轮毂4个受载方向的瞬态应力结果。

图5 弯曲载荷耦合加载示意图

3.2 径向载荷疲劳试验

轮毂径向载荷疲劳试验用于模拟汽车在非平整路面行驶时，汽车轮毂受到车身自重和来自垂直地面方向冲击力而发生疲劳失效的场景，其试验方法如图6所示，使用螺栓将汽车轮胎及轮毂固定在转动盘上，通过试验机中旋转的转鼓驱动车轮转动，并对车轮施加径向的 压力。

图6 轮毂径向载荷疲劳试验示意图

试验中，施加在车轮上的径向载荷值为

式中，F为径向载荷；F为车轮最大额定载荷（由车轮或轮毂制造厂规定）；K为强化试验系数，其值见表2。

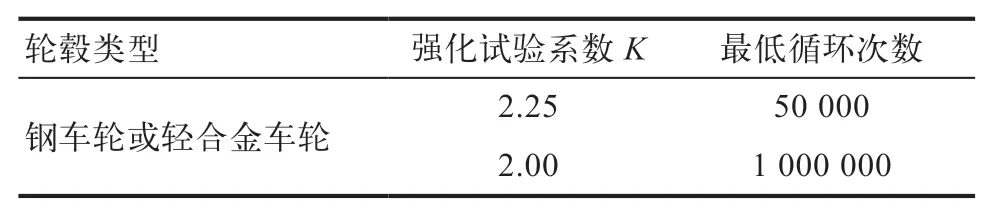
表2 轮毂动态径向疲劳试验要求

21世纪初，文献[27]研究了铝合金汽车轮辋应力及位移分布后发现，在轮毂动态径向疲劳试验中，轮胎压力对轮辋的作用可等效替换为施加在轮辋上的径向分布力W，如图7所示，径向分布力按余弦特征作用在轮辋上，其范围约为40°，径向分布力的值从轮毂中线至两侧20°角度逐渐减小。

图7 轮毂所受径向载荷等效替换作用力示意图

定义车轮所受最大径向分布力W，则车轮径向分布力W的表达式为

式中，θ为加载偏转角；θ为最大加载偏转角。

则车轮所受径向力的合力F的表达式 (4) 为

式中，b为轮胎座受力宽度；r为轮胎座半径。

实际试验中，需对轮胎充加大于轮胎使用气压的试验气压。文献[28]在研究导致车轮动态径向疲劳失效的原因时发现，轮胎的气压对轮毂承受径向载荷的疲劳寿命有很大的影响。文献[29]通过分析轮胎气压对轮辋的作用效果发现，轮胎气压以两种方式作用于轮辋：①以法向力均匀作用于整个轮辋外表面；②以侧向力均匀作用于整个轮辋两侧内环面。

轮胎气压对轮辋侧向作用力W的表达式为

式中，p为轮胎试验气压；r为轮胎充气后内面半径。

而轮辋单侧受到的侧向力约为W的1/2，所受的侧向载荷p表达式为

式中，s为单侧轮辋与轮胎外侧的接触面积。

文献[29-34]建立了轮毂的有限元模型，将轮胎气压等效替换为表面压力施加在轮毂轮辋的外表面，将轮胎对轮辋的径向作用力采用余弦函数的方式施加于轮胎圆心与转鼓圆心连线双侧40°范围内，如图8所示，并将轮毂所有螺栓孔的6个自由度进行全约束，通过静力学分析获得仿真结果，最后基于材料的S-N疲劳寿命曲线来预测车轮在径向动态载荷作用下的疲劳寿命。

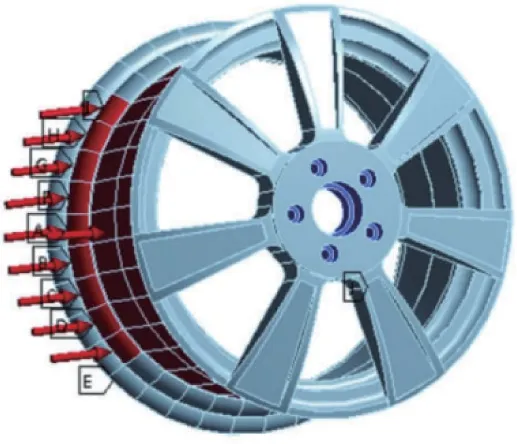
图8 轮毂径向载荷施加示意图

其中，文献[29]考虑了轮胎侧向力对轮毂轮辋的作用，在轮辋两侧施加了侧向载荷，得到了更为准确的分析结果。文献[30]选取了轮毂上3个特殊位置点进行静力学应力分析，使径向载荷作用效果更接近实际工况。文献[31]在获得轮毂静力分析结果后，运用nCode Design Life软件进行了疲劳分析，预测了车轮疲劳寿命。

文献[31，33-34]为模拟出车轮转动时受径向力作用的效果，假设了车轮静止不动，而载荷围绕车轮圆周旋转。通过多个载荷步的方法，使径向分布力依次转过一定角度，获得了轮毂各个方向承受径向力的应力结果，以确定整个轮毂上最大的应力点。

3.3 13°冲击试验

轮毂冲击试验用于模拟汽车在行驶过程中，轮毂受到轴向冲击载荷而发生失效的场景，冲击角度包括13°、30°及90°三种，多选择13°，使用螺栓将汽车车轮安装在与冲头垂直下落方向成13°夹角的固定架上，冲击块底面位于车轮轮辋轮缘最高点2 302 mm处，其冲击面与轮辋的重叠范围为25 mm，长度与宽度分别应大于375 mm、125 mm。

试验中，车轮所受的冲击载荷为

式中，D为冲头质量；W为轮毂最大静载荷。

文献[35-42]建立了包括冲击块、车轮总成和试验台在内的有限元模型，如图9所示，考虑了冲击力对材料性能的影响，模拟了冲击试验的全过程，得到了冲击块在冲击过程中的动能、冲击力、能量变化曲线及轮毂的应力分布云图，预测了轮毂可能发生失效的位置。

图9 轮毂13°冲击试验有限元模型

其中，文献[35-37]等在建立轮胎模型时采用了Mooney-Rivlin 模型描述轮胎橡胶部分的超弹性非线性特征，考虑了轮毂、轮胎材料的不同属性，并讨论了轮毂网格最小尺寸与仿真最大时间步长的关系，Mooney-Rivlin模型表达式为

式中，E为修正的应变能；C和C为待定的材料参数；I和 I为第一和第二Green应变量。

文献[38-39]考虑了轮毂安装的预应力，并将橡胶支座采用弹簧-阻尼单元进行模拟，对轮胎和轮毂贴合处进行钢化处理，通过试验结果验证了方法的合理性。文献[40]采用梁单元对轮胎帘线和钢丝建模，在轮辋外表面及轮胎内表面施加面载荷以模拟胎压。文献[41]将轮毂总体塑形功作为失效判据，将最大应变能密度与之比较，来预测轮毂失效点。文献[42]在轮胎、轮毂、试验台间设置罚函数接触类型，以模拟各结构的实际接触情况。

文献[43-44]仅建立了轮毂、轮胎和冲击块的模型，通过在轮毂螺栓孔处施加全约束以固定轮毂，设置了接触条件及轮胎胎压，得到的仿真结果与实际试验结果一致。其中，文献[43]通过仿真结果得到了轮毂应力集中的主要时间段，并确定了冲击块下落至最低位置时，轮毂所受应力最大。文献[44]将冲击块底端调整至紧挨轮胎顶端，如图10所示，根据下落高度计算出冲击块初始速度值，大大节省了仿真时间。

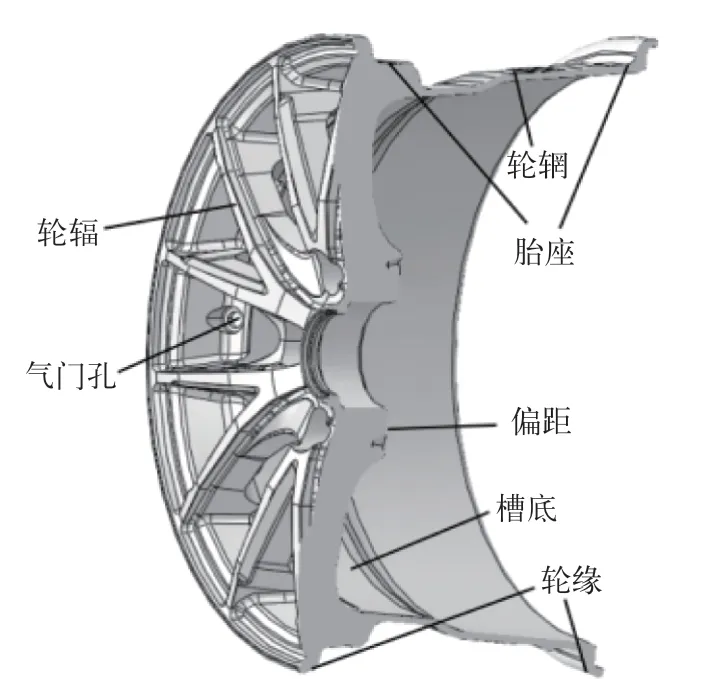
图1 轮毂基本结构示意图

图10 冲击块底端紧挨轮胎顶端示意图

文献[45]在上述研究方法基础上，仅建立冲击块和轮毂的有限元模型，引入轮胎吸能系数η（通过试验确定其值约为20%），计算出系数影响下冲击块与轮毂接触的瞬时速度v，其表达式 (9) 如下，将冲击块设置于轮毂顶端，并将瞬时速度v作为初始条件施加于冲击块，进一步简化了轮毂动态冲击过程，缩短了仿真时间。

式中，g为重力加速度；H为冲头底端距离轮胎顶端的高度差。

以上研究者采用的仿真方法，尽管其数值结果比较接近真实试验结果，但要求设置模型的材料、摩擦系数等基本参数较多，且非线性动力学计算时间过长，因此将冲击动力学问题转化为结构静力学问题，是解决上述问题的有效方法。

文献[46]通过试验发现轮毂受到的冲击载荷值可近似以正弦激励函数表述，其表达式为

式中，t为冲击力作用时间；F为冲击过程中轮胎所受最大冲击力，其表达式为

通过上述简化，只需获取冲击过程中冲头和车轮的接触时间，即可将瞬态冲击动力学问题转化为静力学问题，从而将冲头冲击轮胎的动态模拟转化为冲击载荷作用于轮毂的静态力学分析。

文献[47-48]采用静力学分析法，仅建立轮毂有限元模型，不考虑轮胎对轮毂产生的影响，将冲击峰值载荷加载到轮毂受冲击位置，如图11所示，即冲头与轮缘边25 mm的区域，将胎压载荷施加在轮辋表面，对轮毂法兰螺栓施加全固定约束，结果表明，仿真结果与试验结果相吻合。

图11 轮毂13°冲击载荷简化加载方式示意图

4 总结

1）在进行轮毂弯曲疲劳试验仿真研究时，首先建立轮毂及试验设备的有限元装配模型，轮毂上圆角、气门孔等特征可删除，并在模型各元件之间添加接触关系。然后对轮毂及其他试验元件赋予材料特性，在加载力臂远端每隔一定角度依次施加数个垂直于加载力臂轴线的载荷，然后约束轮辋与夹具接触位置节点全部的自由度，以获得轮毂在静态弯曲载荷作用下的应力分析结果。最后基于应力结果和轮毂材料S-N疲劳寿命曲线，采用疲劳分析软件，预测轮毂在弯曲载荷下的疲劳寿命。

2）在进行轮毂径向载荷疲劳试验仿真研究时，首先建立轮毂的有限元模型，在轮毂轮辋的外表面施加等效替换轮胎气压的表面压力，在轮胎圆心与转鼓圆心连线双侧40°范围内对轮辋施加余弦函数方式的径向作用力，然后在轮毂所有螺栓孔节点处施加6个自由度的全约束，以获得轮毂在静态径向载荷作用下的应力分析结果。最后基于应力结果及轮毂材料的S-N疲劳寿命曲线，采用疲劳分析软件，预测车轮在径向动态载荷作用下的疲劳寿命。

3）在进行轮毂13°冲击试验仿真研究时，可选用动态模拟方法：建立包括冲击块、车轮总成在内的有限元模型，考虑轮毂、轮胎及其他元件的材料异同，同时考虑轮毂安装预应力和轮胎胎压，然后在轮毂螺栓孔处施加全约束，并给予冲击块初始速度，冲击轮毂轮缘边25 mm的区域，以模拟13°冲击试验的全过程，得到轮毂应力分布云图，预测轮毂发生失效的位置。

也可选用静态模拟方法：仅建立轮毂有限元模型，不考虑轮胎对轮毂的影响，将峰值冲击载荷加载到轮毂受冲击位置，即冲头与轮缘边25 mm的区域，在轮辋表面施加胎压载荷，在轮毂螺栓孔处施加全约束，以获得轮毂在静态冲击载荷作用下的应力分析结果，预测轮毂发生失效的位置。