重载铁路列车载荷下埋地管道力学行为研究
余鹏,韩金刚,杨建平,欧东方
眉山中车制动科技股份有限公司,四川 眉山 620010
近年来,随着轨道交通的大规模建设和各城市地下管线的增多,地下空间越来越拥挤。轨道交通线路与埋地管道靠近或交叉的现象越来越普遍[1]。列车轨道与地下管道交叉处的管道载荷主要包括重力、土压力等静载荷和车辆通行载荷、地面堆载、温度载荷以及管道内压等活载荷。在车辆交通载荷中,列车载荷是影响埋地管道的重要载荷类型。随着中国经济的发展,铁路运输的载荷和速度不断增加[2],从而导致地表在列车载荷作用下产生的变形的情况越来越普遍[3]。虽然列车不会直接在管道上滚动,但滚动载荷通过地面和土壤的传递最终会影响管道的安全运行。因此,对重载列车载荷作用下埋地管道进行力学分析具有重要的工程实践意义。
已有一系列文献对交通载荷作用下埋地管道的力学性能进行了分析。Wang等[4]建立了一个二维有限元模型来模拟交通载荷作用下聚乙烯管道的性能,并研究了一些参数对管道弯矩的影响。Fang等[5]采用有限元方法研究了交通载荷不同工况下承插式混凝土排水管,探讨了载荷类型、载荷位置和埋深对管道力学响应的影响。Xi等[6]利用数值模拟方法分析了交通载荷作用下燃气聚乙烯塑料(Polyethylene,PE)管的可靠性,并用交通载荷的单随机变量计算了埋地管道的应力分布。Alzabeebee等[7]利用有限元模型研究了埋置混凝土管道在英国标准交通载荷下的响应,给出了管径和回填高度对管壁弯矩和管道周围土压力的影响。
此外,在交通载荷方面也有一些类似的研究。Xia等[8]进行了铁路列车诱发振动对周围地面及附近建筑物影响的试验研究,得到了列车速度、车辆载荷等关键参数的影响。Bucinskas等[9]提出了车-桥-土耦合系统的计算模型。Zhai等[10]提出了基于车-轨耦合动力学和有限元法的车-轨-地综合动力学模型,并介绍了列车诱发地面振动的现场试验。Yang等[11]采用有限元/无限元方法,参数化研究了地基土性质对高速列车振动传递的影响。
以往对管道力学行为的研究主要集中在土体变形下的管道。如Vazouras等[12]研究了埋地X65和X80 管道穿越走滑断层的力学行为,讨论了穿越角度对几种土和管道参数的影响。Zeng等[13]提出了一种管道应变和变形的分析方法,在数值模型中使用等效弹簧来研究管道力学性能的影响。Kouretzis等[14]提出了一种分析方法,用于估算地下管道在永久性地面沉降和隆起作用下的内力和应变。Demirci等[15]建立了一个新的实验来研究逆断层作用对埋地管道的影响,并将实验结果与有限元分析结果进行了对比,以验证有限元模型。
虽然交通载荷方面已有大量的研究工作,但对重载列车载荷作用下埋地管道的力学行为研究较少,对埋地管道进行应变分析十分重要。埋地管道的弯曲变形是由土压力引起的非线性问题,弯矩沿管道轴向分布不均匀,土-管相互作用是一个不容忽视的重要问题。基于此,本文研究了重载列车载荷作用下埋地管道的力学行为,建立了关于列车载荷、列车轨道、轨枕和管道的有限元模型,采用接触算法精确地考虑了管道与土的相互作用。在数值模型的基础上,选取典型参数对管道进行力学性能分析,结果可为管道在工程实践中的应用提供理论参考。
1 有限元模型的建立
1.1 材料属性
本文中管道采用线性各向同性应变硬化模型,管道钢级为X65 钢管:屈服强度为448.5 MPa[16],杨氏弹性模量为210 GPa,泊松比为0.3,密度为7 800 kg/m3。土和道砟采用Mohr-Coulomb 模型:密度为ρ,内聚力为c,摩擦角为f,杨氏弹性模量为E,泊松比为μ。文中假设土体的膨胀角为0[12],同时假定土体和道砟为各向同性材料,不含砾石或孔隙。列车轨道和轨枕采用线弹性模型[17],轨道为75 型重型轨道,轨枕采用Ⅲ型钢筋混凝土。详细参数见表1[17-19]。
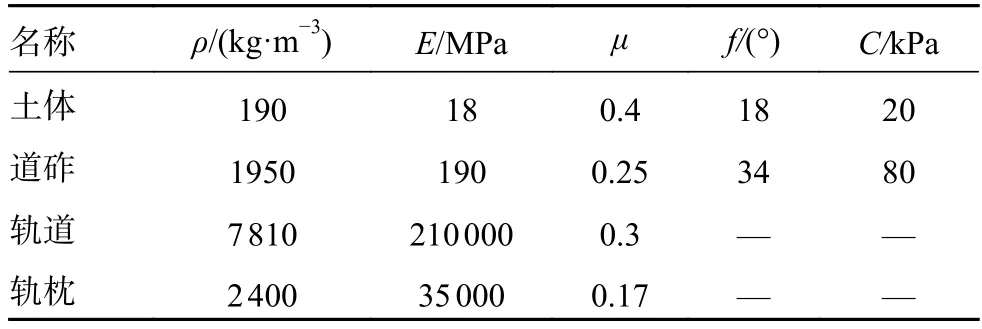
表1 材料参数
1.2 有限元模型
列车运行过程中产生的载荷主要来自轮轨相互作用。本文以设计轴重300 kN 的C80 型运煤重载列车为研究对象,采用竖向载荷对埋管进行力学性能分析。
采用通用非线性有限元软件建立有限元模型,管径为660 mm、管道壁厚8 mm。管道周围土体与管道长度相同,整体土体模型设定为16 m×8 m×5 m。管道中心距地面1.5 m。列车轨道横截面简化为矩形,横截面宽15 cm、高15 cm[17]。轨距采用标准轨距1.435 m[20]。轨枕截面简化为长方体,长2.5 m、宽0.3 m、高0.23 m。轨枕沿轨道的纵向间距为0.6 m[17]。几何模型示意如图1所示。
在有限元模型中,列车施加的载荷与空间上的车轮相对应,因此可以在轮轨接触点施加集中力来描述轮轨间的相互作用力[17]。列车的移动载荷可等效为静载荷,根据规范规定的列车轴重计算车轮静载,再乘以系数,约为最大静载的1.3 倍用来模拟列车载荷[18,20]。以相邻2 节车厢连接位置为例,在车轮和载荷密集分布的位置,共有4 组车轮,如图1 所示,同一车厢内相邻2 个车轮之间的距离为1.8 m,不同车厢内相邻2 个车轮之间的距离为1.5 m[17,20]。

图1 几何模型示意
考虑到载荷和几何结构的对称性,有限元模型采用1/2 模型计算[21]。在数值分析中,土体的xy和y-z表面在z方向和x方向分别采用法向约束。土体的底面(底部x-z平面)在x、y、z方向均受到约束,上部x-z面为自由面[21],在对称平面采用对称约束。采用Dynamic/Explicit 分析方法模拟加载过程,数值分析分3 步进行:重力加载步、内压加载步和列车载荷加载步。在重力加载步骤中,重力加载应用于整个模型;在内压加载阶段,内压作用于管道内表面;在列车载荷步骤中,列车载荷沿y方向施加在列车轨道上。有限元模型如图2 所示。采用表面接触算法模拟土与管道的相互作用,该算法可以实现土与管道的分离。采用摩擦系数来描述界面摩擦,摩擦系数等于0.3[16]。

图2 有限元模型
土体、轨枕和列车轨道均采用八节点减缩积分单元(C3D8R)模拟,管道采用四节点壳单元(S4R)模拟。为了得到合适的网格划分方法,进行了结果收敛性研究,如图3 所示。因此,本研究中使用的网格方法如下:在管道的圆周方向,将其离散为40 个等尺寸的连续单元。在管道纵向上,对列车轨道下方管道轴向1.25 m 长的管段进行网格细化(40 个等尺寸元件),而管道末端采用较粗的网格。

图3 网格敏感性分析
2 计算结果分析
当管径和壁厚分别为660 mm 和8 mm、施加的列车载荷为300 kN 时,图4 所示为管道的Von Mises 应力分布。结果表明,高应力区出现在管道中部,位于列车两轨道中间,高应力区的形状为椭圆形。此外,在距列车轨道中间约3 m 的距离处也存在高应力区域,但比管道中部的高应力区域小。在管的顶部,管中间的内表面(B 点)的应力大于外表面(A 点),但在管的末端是相反的。在管道的底部,管中间的外表面(E 点)的应力大于内表面(F 点),管道内外表面的应力相差较小。在管道侧面,内表面(D 点)的应力比外表面(C 点)的应力较大。

图4 管道Von Mises 应力分布
图5 所示为管道的轴向应变分布及管道中部截面应变曲线。结果表明,高应变区和高应力区的位置基本一致。在管道顶部,由于列车载荷,管道中部受到压缩,管道末端受到拉伸;管底情况与管顶情况相反,管内外表面应变相差较小,仅在管道中间有略明显的差异,且外表面应变较大。其主要原因是在列车载荷作用下,土体沉降引起的管道弯曲变形首先作用在管道外表面。

图5 管道轴向应变分布
图6 所示为管道的位移分布。管道的横截面仍然保持为圆形,最大竖向位移在管顶,最大水平位移在管侧。因为管顶主要承受列车载荷引起的土体沉降压力大于管底所致。

图6 管道位移分布
3 影响因素分析
3.1 列车载荷影响
重载列车作用在管道上的载荷在真实情况下是随机的。本节研究了不同列车载荷作用下埋地管道的力学性能。图7 为不同列车载荷下管道的Von Mises 应力分布。随着列车载荷的增加,高应力区沿管道轴向扩展,管道内外表面最大应力增大,变化率明显增大。内表面应力较大,最大应力位于管顶内表面。当列车载荷从150 kN 增加到350 kN 时,最大应力增加约60 MPa。因此,当列车载荷较大时,埋地管道可能存在危险。
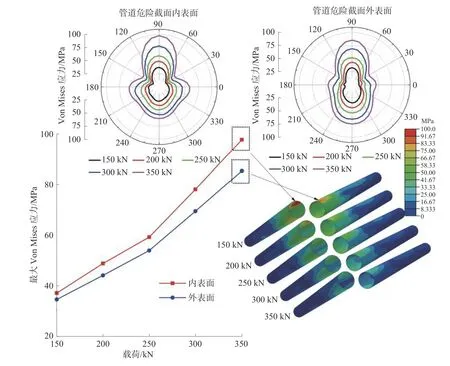
图7 不同列车载荷下管道应力分布
图8 为不同列车载荷下管道的轴向应变分布。随着列车载荷的增加,管顶和管底最大应变增大,变化率基本不变。在管道中部,管顶仍处于受压状态,管底处于受拉状态。另外,列车载荷为150 kN 时,管端轴向应变很小,管道弯曲程度较小。

图8 不同列车载荷下管道轴向应变分布
图9 为不同列车载荷下管道的位移。当列车载荷从150 kN 增加到350 kN 时,最大水平位移略有增加,而最大垂直位移明显增加,由6.4 mm增加到11.5 mm。随着列车载荷的增加,管道的横截面呈略微的椭圆形。管顶竖向位移大于管底,由于列车载荷主要由管顶承受,管道的周向变形较为均匀。另外,随着列车载荷的增加,管顶竖向位移明显增大。

图9 不同列车载荷下管道位移
3.2 管道埋深影响
在列车载荷传递到管道之前,管道周围土体首先发生变形,因此周围土体的变形能力会对管道产生影响,列车载荷引起的附加力随着埋深的增加而逐渐减小。本节考虑了埋深为0.5~3 m 的管道,研究埋深对列车载荷作用下管道力学性能的影响。列车载荷为300 kN,管径660 mm,壁厚8 mm。图10 所示为不同埋深管道的Von Mises应力分布。随着埋深的增加,管内外最大应力减小,变化率减小。当埋深大于2.5 m 时,内外表面差异很小。因此,对于承受列车载荷的管道,应增加埋深。

图10 不同埋深下管道应力分布
图11 所示为不同埋深下管道的轴向应变分布。随着埋深的增加,管道的最大应变减小。管顶轴向应变呈线性变化,管底轴向应变变化率减小。当埋深大于2 m 时,管端轴向应变很小。

图11 不同埋深下管道轴向应变分布
图12 所示为不同埋深管道的位移。埋深从0.5 m 增加到3 m 时,埋深对管道竖向位移的影响更为明显。埋深大于2 m 时,最大水平位移略有减小,变化率较小;随着埋深的增加,管道横截面椭圆度减小。这是因为当埋深较大时,列车载荷引起的管道周围土体变形较小,使得整个管道承受的载荷较小。
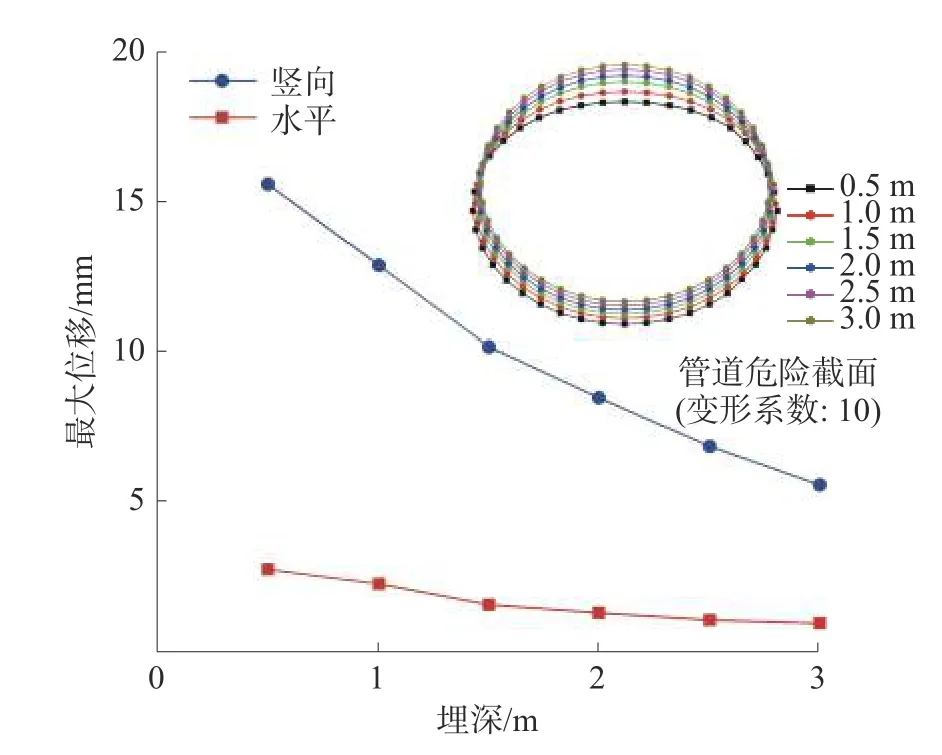
图12 不同埋深下管道位移
3.3 管道内压影响
内压是管道的一个重要工作载荷,在实际应用中,管道的输送压力会有所不同。因此,本节考虑了0~5 MPa 的内压。假设列车载荷300 kN,管道埋深1.5 m,管径660 mm,管厚8 mm。图13所示具有不同内压的管道的Von Mises 应力。管道最大应力变化明显,随着内压从0 MPa 增加到5 MPa,最大应力从78 MPa 增加到250 MPa。当内压大于2 MPa 时,整个管道有大面积的高应力区。因为当内压较大时,列车载荷对管道应力的影响小于内压的影响。因此,在列车载荷作用下,压力管道比无压力管道危险。

图13 不同内压下管道内表面应力分布
图14 为不同内压下管道的位移。当内压由0 MPa增大到5 MPa 时,竖向位移由10.2 mm 减小到8.4 mm。水平位移的变化率小于竖向位移。随着内压的增大,管道横截面椭圆度减小。这是因为内压能使管道产生较高的刚度,它能抵抗列车载荷在竖向方向引起的管顶变形。

图14 不同内压下管道位移
4 结论
本文研究了重载列车载荷作用下埋地管道的力学性能。建立了考虑列车载荷、列车轨道结构和土管相互作用的有限元模型。研究了列车载荷、埋深和内压对管道受力的影响。主要结论如下:
1)管道高应力区位于列车轨道下方,高应力区形状为椭圆形。在管顶,管内表面的最大应力大于管外表面的最大应力。在管道底部,管道外表面的最大应力较大。在轨道下方的管段中,管顶受压,管底受拉。管道内外表面的应变相似。管道的横截面可以保持圆形。管道最大竖向位移和水平位移分别位于管道顶部和侧面。
2)管道的最大von-Mises 应力、轴向应变和位移随列车载荷的增大而增大,随埋深的增大而减小。内压会增加管道的von-Mises 应力,但位移会减小。

