桥梁冲刷计算公式的应用分析

曾桂华，程素珍，张庆丽

（1.山东省水利科学研究院，山东 济南 250014；2.山东省科源工程建设监理中心，山东 济南 250014）

1 概述

随着我国经济的高速发展和建筑水平的快速提高，跨河桥梁的建设数目越来越多，规模越来越大，部分墩台不可避免地位于河道的行洪断面内，在一定程度上阻碍河道行洪，改变局部河道水流流态，对河道行洪安全造成一定影响，桥墩部位的冲刷，在一定程度上也影响桥梁自身安全。为了河道的行洪安全和桥梁自身运行安全，对桥梁墩台进行冲刷分析计算是必要的。冲刷深度计算公式的选择正确与否、成果是否合理，会直接影响到评价结论，也是水行政主管部门对桥梁建设方案进行审查的重点内容之一。

1.1 河床自然演变冲刷

1）纵向冲刷。纵向冲刷计算公式规范一般采用一维河床冲淤数学模型进行计算，采用上下断面河道含沙量的变化推算一般冲刷深度。受目前理论研究水平的制约，根据理论公式计算的天然河道挟沙能力成果，存在较大偏差，对设计人员来说确定纵向冲刷成果难度较大。

2）横向冲刷。横向冲刷是河槽横向变动引起的自然演变冲刷，对于天然河道，横向冲刷是不可避免的，但考虑到在山东地区，按地貌大体分为黄泛平原区和山丘区。对于黄泛平原区，基本以淤积为主，对于山丘区，由于局部侵蚀基准面抗冲刷能力较强，短期的自然演变冲刷也比较小，因此，考虑到目前计算方法不太可靠，且短时间变化很小，在冲刷计算中，一般不再考虑河床自然演变冲刷对墩台的影响。

1.2 桥下一般冲刷

因桥梁墩台的修建，压缩了河道的行洪断面，致使桥孔上游水流急剧集中流向桥孔，河床切应力迅速加大，在桥下河床断面内发生的冲刷称为桥下一般冲刷，随着其冲刷发展桥下段面逐渐增大，流速降低，至泥沙输送和交换达到暂时的平衡状态时，一般冲刷便趋于停止。通过计算某一设计频率洪水冲刷后的最大水深计算桥下一般冲刷深度，一般采用《公路工程水文勘测设计规范》（JTGC30－2015）中推荐的公式进行计算。

河床土质类别直接决定一般冲刷公式的选择，所以进行桥下一般冲刷计算时，首先根据河床的实际土层情况，区分河床是非粘性土还是粘性土，然后对河槽和河滩部分分别采用规范推荐的公式进行计算。

1.3 墩台局部冲刷

墩台对水流的干扰造成的局部冲刷是一个非常复杂的动力过程，影响冲刷坑的深度和大小的因素较多，墩前行近流速、桥墩宽度、墩体形状、床沙粒径、河流水深、水流交角等都是密切的影响因素。桥墩影响下的紊流是产生局部冲刷的内因，但紊流冲刷问题目前没有具体的计算理论，《公路工程水文勘测设计规范》（JTGC30-2015）中局部冲刷计算公式综合考虑了影响桥台局部冲刷的外部因素，并进行了水槽模拟试验验证，其计算结果基本可靠、合理。

2 工程实例

2.1 工程概况

故献大桥位于高密市故献村东南的胶河中泓线桩号K43+595 处，为原址拆除重建，桥梁全长125 m，跨径组合6×20 m，共有7 个桥墩，其中5 个桥墩布置在河槽内，2 个桥台位于河滩上，桥墩直径均为1 500 mm。上部结构采用预应力混凝土空心板，桥面连续；下部结构采用U 型桥台扩大基础，柱式墩扩大基础。

桥址处河道为复式断面，河槽底宽102.68 m、底高程24.3 m，边坡1∶2，河滩宽度6 m、滩顶高程29.39 m，两岸岸顶高程31.59 m。河道设计洪水标准为20 年一遇、设计流量680.00 m3/s、设计洪水位为30.49 m，故献大桥设计洪水标准为100年一遇、设计流量2 218 m3/s、设计洪水位为31.69 m。

经对河槽地层岩性的综合分析，故献大桥处地层性质判别为粉土，冲刷计算时按非粘性土公式进行，故献大桥的冲刷计算时分别按64-2 简化式和64-1 修正式进行计算。为节省篇幅，只对河槽进行一般冲刷计算和分析。

2.2 非黏性土河槽一般冲刷计算

本次计算工况采用20 年一遇洪水的设计流量，根据《公路工程水文勘测设计规范》（JTGC30-2015） 中推荐的两个非黏性土河槽一般冲刷公式分别进行计算，用《堤防工程设计规范》（GB50286-2013）推荐的计算公式进行验证。1

）64-2 简化式。

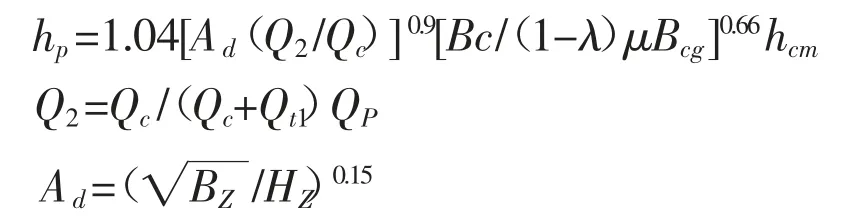
式中：hp为一般冲刷后的桥下最大水深，m；QP为相应计算频率的河道设计流量，m3/s；Qc为未建桥天然河槽设计流量，m3/s；Q2为相应计算频率的桥下河槽设计流量，m3/s；Qt1为未建桥天然桥下河滩设计流量，m3/s；Bz为造床流量时的河槽宽度，m，123.04 m；Bcg为设计桥长范围内河槽的宽度，m，取123.04 m；μ 为桥墩对水流的侧向压缩系数，μ 取值为0.97。

经计算hp为1.43 m。

2）64-1 修正式

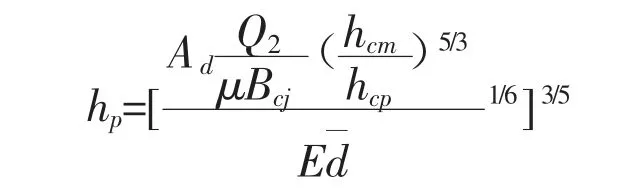
式中：Bcj为河槽部分的过水净宽，m，项目中采用与平滩水位相应的宽度作为造床流量时的河槽宽度，即123.04 m；hcq为河槽部分的平均水深，m；d 为河槽部位泥沙的平均粒径，mm，根据地质资料，本项目取0.08 mm；E 为和汛期河流含沙量相应的系数，根据河道的含沙量，项目取0.66；其余符号含义同前。经计算hp为1.77 m。

根据对本工程的实际冲刷的跟踪测量调研，反推出的一般冲刷值为1.51 m，64-2 简化式计算成果与实际测量值的误差为17.22%；64-1 修正式计算成果与实际测量值的误差为5.30%，可见64-1 修正式计算成果更接近于实际。

2.3 非黏性土河槽一般冲刷计算公式的由来及存在的不足

当桥梁上游天然断面来沙量G 大于桥下冲刷区排出沙量G 时，床面则淤积；来沙量小于排沙量时，床面则冲刷；来沙量与排沙量相等时，冲淤平衡。推移质运动是产生河槽冲刷的主要因素，根据推移质输沙量平衡条件，导出桥下河槽断面64-2 一般冲刷计算公式。1964 年中国土木工程学会“桥梁冲刷计算学术会议”把“64-2 计算式”作为推荐的桥下一般冲刷计算公式之一写入规范，由于其计算考虑影响因素较多，计算繁琐，1985 年西安公路学院对“64-2 计算式” 进行简化，即为“64-2 简化式”，计算简便且其精度与“64-2 计算式” 相当。它是依据河槽输沙平衡理论建立的公式，并参照外国相应同类公式和我国多年桥梁洪水冲刷实测观测资料进行了验证修正，具有丰富的实践基础和坚实理论，其计算成果比较符合桥下河流一般冲刷深度的实际情况。

64-1 修正式也是1964 年中国土木工程学会在会议上推荐的桥下一般冲刷计算公式，《公路桥位勘测设计规范》（JTJ062-91）对64-1 计算式作了局部修正，即为64-1 修正式。

这两个公式的建立都是依据水力学连续性原理，依据冲止流速的概念建立的适合非黏性土河槽的一般冲刷计算公式。在山东省水利厅2021 年度重点调研课题“涉河、涉水建筑物对洪水的影响以及防护措施落实、运行情况的调研报告”中，对已竣工的山东省境内20 个涉河建设项目、50 个单项工程为对象进行了修建涉河项目的河槽实际冲刷情况调研得知，对非黏性土河槽，泥沙平均粒径对计算成果影响较大，公式64-1 修正式更接近于实际情况。

3 结论及建议

1）桥梁墩台冲刷是一个复杂河槽再造过程，是水流、结构物和泥沙之间三维的相互作用问题，目前尚无符合计算精度要求的单一公式，只能将复杂的冲刷过程分解为河床自然演变冲刷、桥下一般冲刷、墩台局部冲刷三个相对独立部分，并假定三部分冲刷过程依次进行，采用不同公式分别计算，将三部分计算结果相加，作为桥梁墩台的最大计算冲刷深度。对于不同条件下的桥梁墩台冲刷机理尚有待进一步研究。

2）桥下冲刷计算公式形式较多，各行业根据冲刷影响因素的侧重均相应提出了本专业的计算方法，但所有公式的理论基础均来自国外的同一参考资料，虽进行了几十年研究，理论上缺少创新，当代跨河建筑物的形式和结构都发生了较大变化，需要开展桥下冲刷计算理论研究。

3）由于计算理论和方法的局限性，应进一步加强在役工程冲刷观测，积累工程经验，为今后类似工程项目冲刷计算提供更加可靠的依据。