并网逆变器早期故障诊断

魏胜风， 帕孜来·马合木提， 樊鹏帅

(新疆大学 电气工程学院， 乌鲁木齐 830047)

0 引 言

大功率并网逆变器作为风电、光伏系统等电能转换与电网衔接的核心设备，其结构复杂，工作环境恶劣，具有极快的模式切换，它们是电力系统中较薄弱的部分且具有较高的维护投入。电力电子电路中存在多种非线性元件，电路的工作状态是离散的，是一个典型的混杂系统[1]。多电平并网逆变器较广泛的应用于高压、大功率和高品质的电力系统中，虽然效率不断提高，但大量的元器件难免增加了故障发生的概率[2]。逆变器的早期故障诊断对于确保电力系统能安全且稳定的运行具有重要的现实意义。

NPC型逆变器是电力系统中应用广泛的电力电子转换器之一，例如：不间断电源、静止无功补偿器、有源电力滤波器等。然而，其常工作于较高的频率、电压及恶劣环境下，会发生偏离标称值的早期故障，为避免逆变器可控开关器件由参数偏移引起的软故障逐渐转化为不可逆的具有破坏性的硬故障，所以对早期参数性故障诊断非常重要。本文引入了基于GARRs的BG诊断方法在NPC型逆变器中的应用设计，运用反应模式及参数等信息的GARRs对该逆变器进行早期参数性故障诊断。通过20-sim BG软件仿真研究，该方法能检测、定位出IGBT元件的早期参数性故障，为后续该领域的研究提供相关参考。

1 参数性故障

参数性故障是指元件参数值较标称值产生较大偏移而引起的一类故障模式[3]，元件的参数性故障表现在其出厂服役后，当其处于快切换系统中或者工作环境又处于高温、高压等恶劣环境所造成的其参数会偏离标称值一定范围的参数性退化，即早期参数性故障。相对于结构性故障，参数性故障更难诊断，在实际中数据集也很难以测量。IGBT参数性故障表现为键合线老化、焊料层、铜基板、硅脂等多层结构受热应力扭曲形变等，导致集电极和发射极压降等发生变化，虽然短时间内是不会造成系统功能的丧失，但伴随着程度的加深，会影响整个并网逆变器的输出[4]。因此，开展逆变器关键元器件的早期参数性故障诊断的研究有利于避免严重事故的发生。

文献[5]比较功率管发生开路故障时逆变器输出三相电流真实值和估计器比较得到残差，通过对残差分析实现硬故障诊断，但无法实施早期参数性故障诊断。文献[6]基于模糊逻辑的策略，依据隶属度函数和模糊关系矩阵将故障和征兆二者联系起来，完成早期故障检测。参数设置具有较强的主观性，阈值仅为常数阈值。文献[7]首次引入增量BG以进行早期故障诊断方法研究，以Boost电路进行验证，但若扩展到多电平逆变器则十分困难；文献[8]使用基于支持向量机的自适应阈值研究，以伺服系统进行仿真，但不能适用于具备极快切换开关模式的系统中。

2 键合图理论

BG理论是Paynter教授于1961年提出的，它是基于能量守恒原理，可对具有不同物理性质的系统(机械，电气，液压，气动等)进行建模，是一种基于功率流图形化表达的系统动力学仿真方法[9]。BG建模主要由键合图元和键组成。键合图元包括: 势源(Se)、流源(Sf)、容性元件(C)、惯性元件(I)、耗能元件(R)、调制器(MTF)，回转器(GY)以及连接图元的共流节点(1)和共势节点(0)等[10]。键则表征键合图元连线间的功率流动。

3 基于全局解析冗余关系的故障诊断

GARRs是通过系统的自组织使系统稳定，通过实际系统与故障模型的系统输出比较得到系统的残差以反映故障信息[11]。其一般表达式为

ri(u,αi,θi,…,Dei,Dfi)=0

(1)

式中：u为系统的输入，i为从DHBG推导的GARRs数量；αi为系统的模式,θi为系统元件参数，Dei、Dfi是系统的势及流传感器的测量值。当元件无参数性故障时，残差应为零或近似零值；当元件有故障时，残差值会随之偏离零值进行响应。最后，通过具有参数及模式信息的 GARRs导出反映故障与残差关系的矩阵即FSM，从而提取故障特征，便于故障检测(Db)与隔离(Ib)。基于BG的GARRs的故障诊断方法关键是在BG模型加入势(流)传感器搭建出DHBG，可使用覆盖路径法或因果法分析DHBG以生成理论的FSM，然后再与标称、参数变化时的系统比较所产生的FSM再次对比，以验证该方法的有效性。GARRs不仅有助于发现故障，而且有助于定位系统的有缺陷部分[12]。能快速检测出逆变器关键元器件的早期故障，然后可通过更换相关组件来有效避免对电力系统有害故障的产生。其系统诊断的具体流程如图1所示，残差测量时势、流传感器的转化分别如图2、3所示。

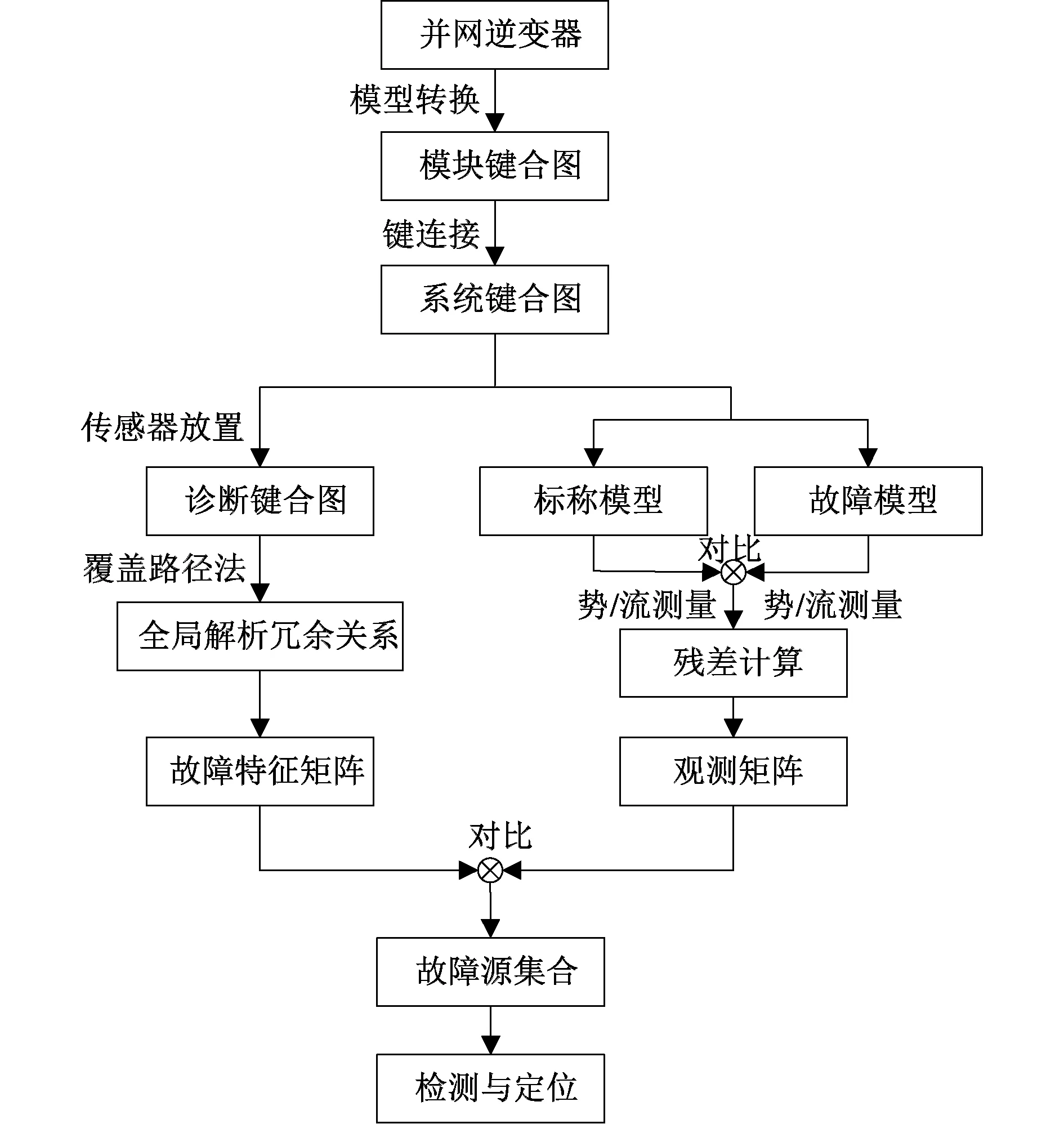
图1 基于GARRs的诊断流程

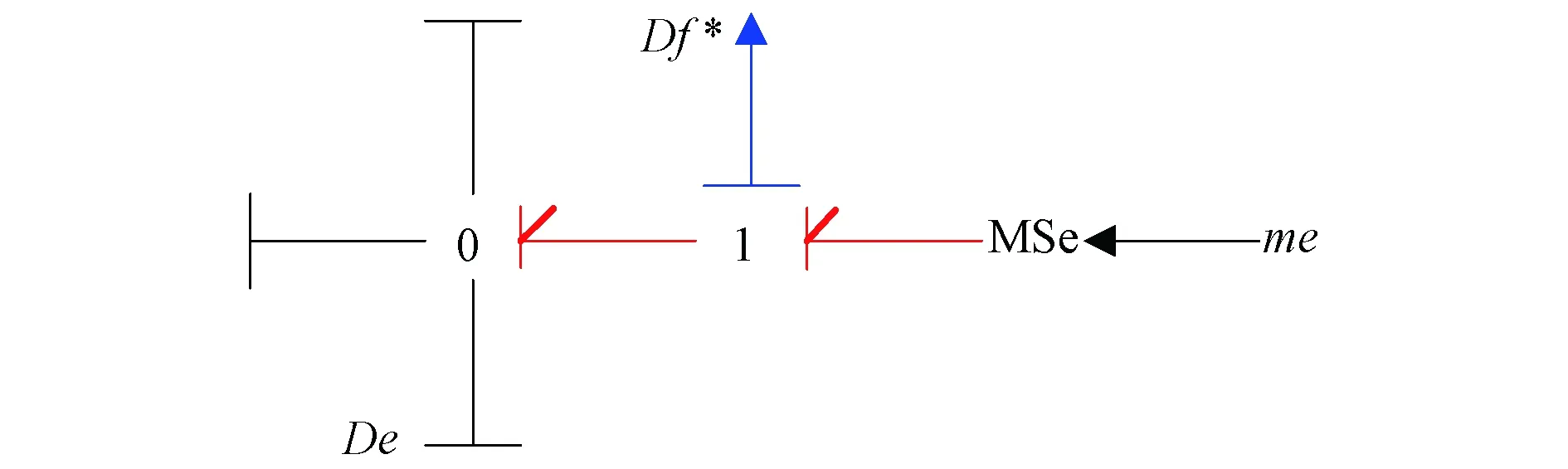
图2 势传感器的转化

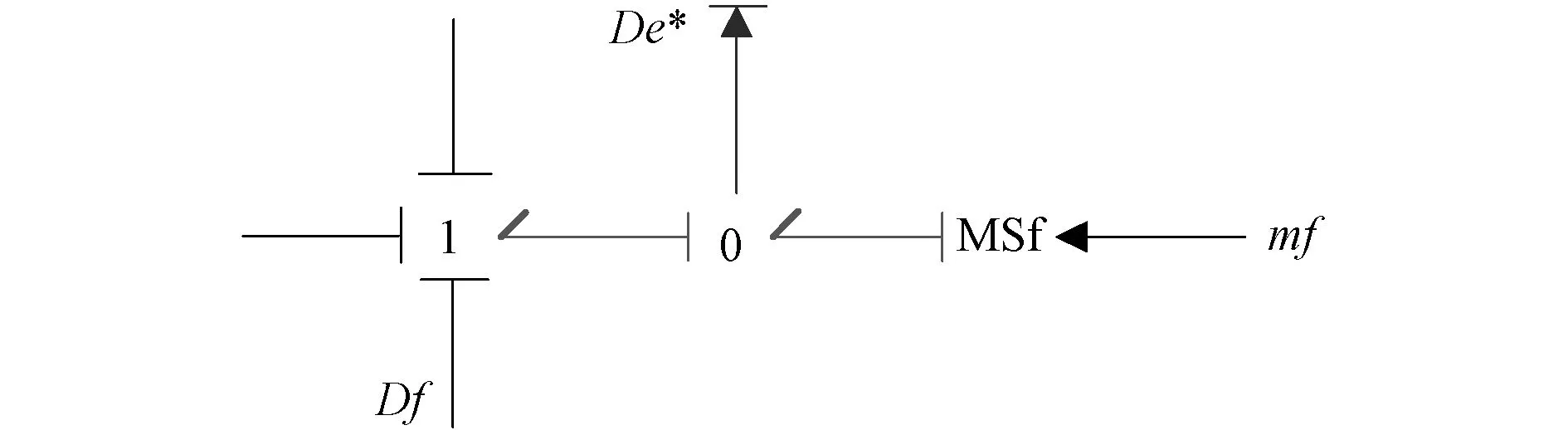
图3 流传感器的转化

4 NPC逆变器的早期故障诊断

4.1 NPC逆变器键合图建模

NPC型三电平逆变器的拓扑如图4。以NPC型逆变器单相为例，开关S1和S3、S2和S4分别是互补工作的，该并网逆变器是具备快切换的开关模式，因此可忽略模式过渡阶段，每相能产生三个电平状态：+Ud/2、0、-Ud/2，即每相的输出可有正(P)、零(0)、负(N)三个开关模式，其电压输出及开关状态如表1所示。

图4 NPC并网逆变器拓扑

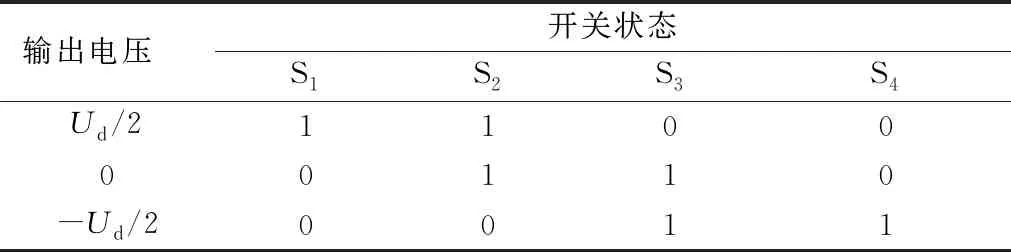
表1 NPC逆变器开关模式

依据BG理论及IGBT工作原理，使用节点法推导的等效电路如图5所示，SWi断开时，Roffi为关断内阻，SWi闭合时，等效内阻Reqi为导通内阻。SWi开关具有开和关两种状态，它是Roni与可调制变换器MTF构成的封装模块然后与Roffi构成整个IGBT键合图模块。由单个IGBT等效电路进而得到半桥BG模型，半桥BG及SWi模型如图6所示，再通过半桥BG的组合，最终得到NPC型并网逆变器的BG模型如图7所示，其中等效内阻Roni=1 Ω，Roffi=1 MΩ，i={1，2，…，12}。限于篇幅，仅考虑Roni在0.02 s时注入10%(5%以内为正常)的参数性故障，即Roni发生10%的参数性退化Roni=1.1 Ω，在0～0.02 s设置为标称值Roni=1 Ω、0.02～0.5 s内处于早期故障状态。系统各元件参数如表2所示。

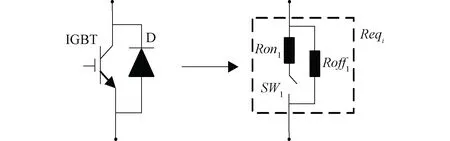
图5 IGBT/Diode及其等效电路

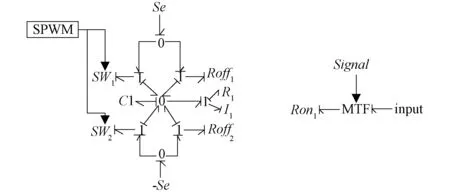
图6 IGBT半桥BG及开关模型

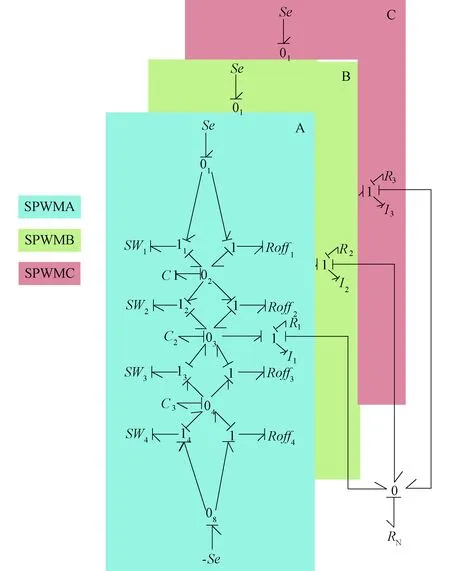
图7 NPC逆变器BG模型

表2 BG模型参数表

此外，通过添加虚拟传感器De、Df，将BG模型转换成DHBG模型，如图8所示，开关元件使用上述开关SWi模拟，开关键合图元件SWi的特性方程如下所示：f=αi2(1/Roni)e[13]。

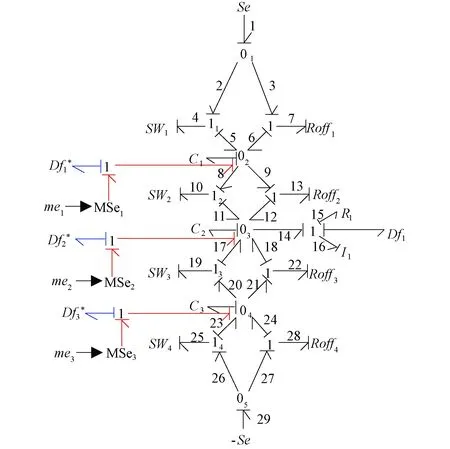
图8 NPC型逆变器A相DHBG模型

本文采用专业BG仿真平台20-sim，只需将本文推导的BG模型通过多通口元件0和1、双通口元件变换器MTF、以及消耗元件R、存储元件C、惯性元件I等基础元件，逐次连接起来进行系统表述，系统自动分配因果关系。对于复杂系统BG模型可能出现代数循环,会使得系统出现紊乱，可添加趋于零值的辅助Ci元件消除，对系统并无影响，在GARRs推导流程中可将其忽略。本文利用覆盖路径法先将搭建好的BG模型依次编键号，通过列写各节点的特性方程用已知量表示出未知量，最后可得所测节点的GARRs式，进而表征出可控性元件出现参数性故障时的残差响应。

4.2 基于GARRs的NPC逆变器故障诊断

本文中SWi的受控节点{11，12，13，14，15，16，17，18，19，110，111，112}对应的布尔变量为{α1，α2，α3，α4，α5，α6，α7，α8，α9，α10，α11，α12}。等效开关由SWi和Roffi组成i={1，2，…，12},Dei、Dfi分别为势、流传感器的测量值。DHBG如图7，以A相的各半桥节点为例，即02，03，04节点的GARRs如下所示，De1，De2，De3为上述各节点势传感器的测量值。准确的NPC逆变器BG及DHBG模型是基于GARRs早期故障诊断的重要条件，测量信号仅通过放置与GARRs式数量一致的势传感器测量单相各半桥节点的势即可。以覆盖路径法列写的特性方程及GARRs式如下。

特性方程为

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

GARRs式为

r1=f5+f6-f8-f9

(10)

r2=f11+f12+f17+f18-Df1

(11)

r3=f23+f24-f20-f21

(12)

(13)

(14)

(15)

FSM是由GARRs推导出的矩阵，以此反映残差集合与故障集合的关系，每行可看成一个二进制向量即一致性向量C=[CK1,…，CKl][14]。

(16)

式中:ri为第i解析冗余关系式；i=1,2,…，l；θj为第j个故障参数；j=1,2,…，k；K为诊断元件的个数。

NPC型逆变器具备不同的工作模态，每个运行模态都对应不同的拓扑，需对每种工作模态进行分析，由于逆变器开关管是在极快模式切换下工作的，则可用或关系合并每个运行模式的FSM，便能对该逆变器系统所有故障进行特征提取。本文合并后的FSM如表3所示，0、1分别代表正常和故障。可看出残差r1对SW1敏感，残差r1与r2对SW2敏感，残差r2与r3对SW3敏感，残差r3对SW4敏感。而且每个元件故障时残差随之响应且FSM具有唯一性，说明该故障是可检测、可隔离，可隔离又指可定位，若FSM不可定位还需开发隔离算法进行参数辨识。所以，当SWi开关中内阻Roni发生早期参数性故障时，根据GARRs推导的FSM可以得出残差对所测元器件的敏感性，元件的可检测性、可隔离性。

表3 合并后的A相FSM

4.3 残差评估的自适应阈值设计

全局解析冗余关系如下式：

GARRs:r(θi)=0

(17)

式中：ri是残差，θi为元件参数，Si为残差灵敏度，表示GARRs对参数的偏导数。

(18)

式中：Δri为残差的偏移量,Δθi为参数的偏移量，因为Roni=1 Ω,设偏差不大于5%的参数性退化为正常范围，考虑BG中Roni类型都一致，所以Δθi=0.05。

Δri=SiΔθi

(19)

实际系统的每个部件都会受到参数不确定性的影响，这些不确定性使参数存在一定的偏差，不再是标称值，暂且不影响元件的正常使用，也不会对系统造成硬性损伤。残差偏移量通式Δri为

(20)

为保证残差评估的鲁棒性，偏移量加入绝对值得

(21)

(22)

<Δri<

(23)

因此，残差的偏移量可表示为

经过上述几个步骤的讲解及Matlab演示之后，学生就比较容易将书中的卷积及差方程求解的理论原理，与应用Matlab进行运算分析的方法联系起来，并且通过数据分析，理解并掌握两个函数的应用方法，从而进一步理解应用卷积求系统输出的方法。

Δrimin<Δri<Δrimax

(24)

偏移量的上下限Δrimax、Δrimin分别为

Δrimin=

(25)

Δrimax=

(26)

rinorm为正常时的残差，因此，自适应阈值Ti为

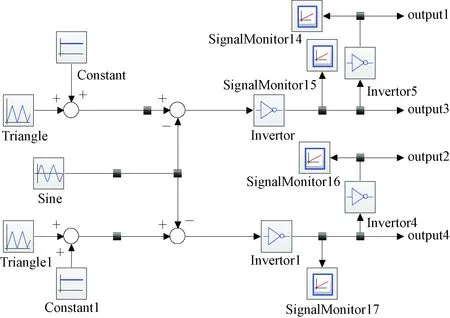
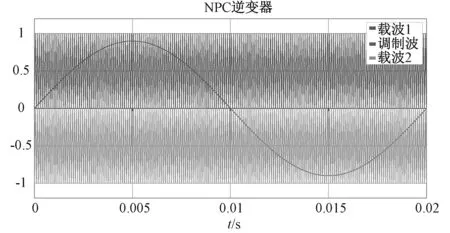
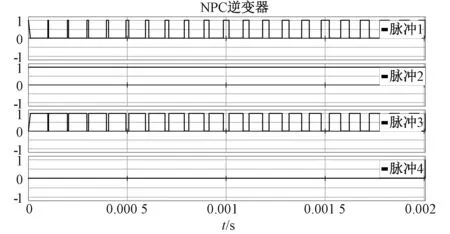
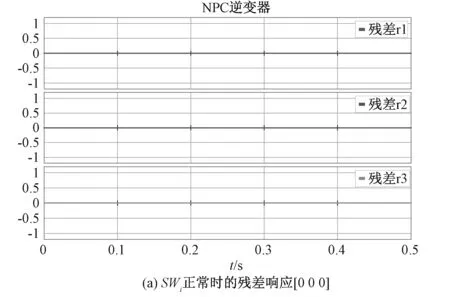
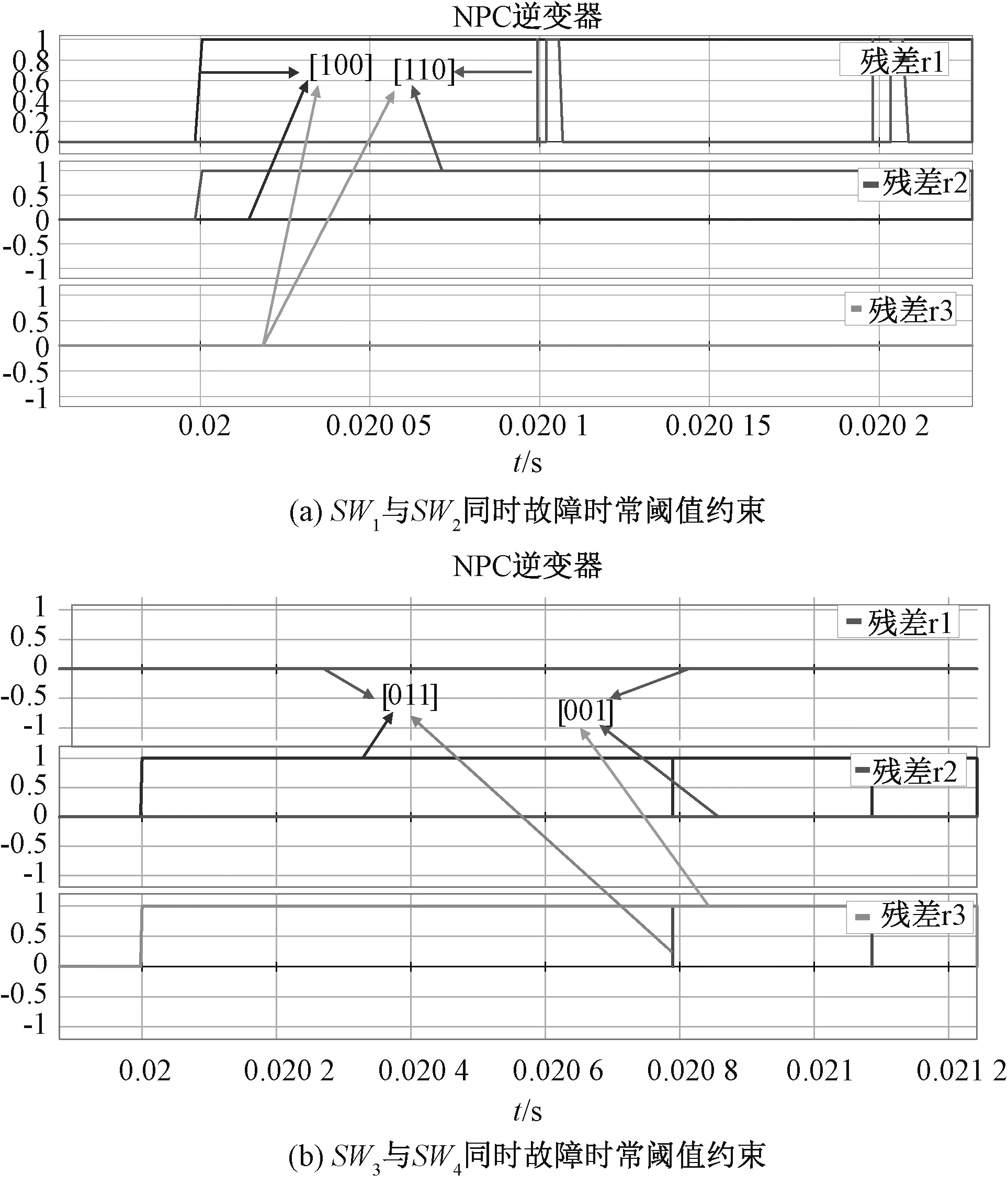
rinorm+Δrimin

(27)

5 仿真验证

调制策略采用的是同相载波层叠[15]，即SPWM来控制NPC型逆变器中IGBT模型，该逆变器调制策略如图9、10所示，驱动信号如图11所示。本文在20-sim BG平台模拟了该逆变器发生参数性故障的特征，当发生早期故障后，逆变器的输出局部电压微小畸变波形如图12所示。逆变器元器件发生参数性故障，输出电压畸变较不明显，所以通过相应残差进行响应，对参数敏感的残差会偏离正常的响应趋势，进行故障报警指示。

图9 20-sim中搭建调制策略

图10 载波层叠调制

图11 产生的驱动脉冲

图12 早期故障时的负载相电压

在20-sim中编写的常阈值残差评估结果能看出，正常状态下的残差响应为[0 0 0]如图13(a)，当SW1在0.02～0.5 s发生10%的参数性故障时，残差响应为[1 0 0]如图13(b)，因其是快切换的系统，为观测自适应阈值评估过程，会使常数阈值约束的残差响应变得密集；SW2发生10%的参数性故障时，残差响应为[1 1 0]如图13(c)；SW3发生10%的参数性故障时，残差响应为[0 1 1] 如图13(d)；SW4发生10%的参数性故障时，残差响应为[0 0 1]如图13(e)。该诊断结果与上文基于GARRs推导的FSM完全匹配，准确反映了残差对所测元器件的敏感性且Db=1、Ib=1，即A相所有SWi早期参数性故障可快速准确检测、定位。

图13 A相单个SWi故障仿真结果

但凭经验的常数阈值存在的弊端是容易造成错误报警，即阈值过大会造成漏报警、过小造成误报警。举例的常阈值设置如下，当残差偏移零值认定为故障报警，即ri大于1或ri小于-1时∣ri∣=1其余情况为0。自适应阈值则可以大大减少这种现象，因其包含了模式信息，能跟随模式不断变化。即使残差幅值很大，也即处在敏感性程度较高时，只要残差不超过阈值上下限，则认为还处于正常的工作状态，反之进行报警。由图13中(b)～(e)中故障指示器的各自适应阈值的约束结果能够看出，依据上文Roni注入10%的早期参数性故障后，自适应阈值的区间会伴随模式等进行变化，残差逐渐超过了自适应阈值进行故障报警。由上文FSM可知每个SWi故障都能够可隔离(定位)，所以多故障也是可以区分的。以SW1、SW2与SW3、SW4双管故障为例进行验证，常阈值约束的局部报警指示如图14(a)中残差响应确实对应FSM中[1 0 0]、[1 1 0]矩阵。自适应阈值是对元件的唯一的动态约束，只要标称值参数偏移过度就会进行报警，多故障时的残差评估过程仍可参考图13。限于篇幅仅给出了部分故障时的自适应阈值约束，相对于常数阈值能有效减少残差评估中的误报现象，残差响应也与FSM相匹配。

图14 A相两个SWi故障仿真结果

6 结 论

本文首先对中点钳位型逆变器工作原理分析的基础上使用节点法建立了准确的BG模型，然后通过加入De、Df传感器搭建出其DHBG模型；其次运用基于BG的GARRs的故障诊断方法快速、准确的得到了全部待测IGBT元件发生早期参数故障时的FSM，进而得到元件的可检测性和可隔离性；最后基于BG残差灵敏度设计的自适应阈值，减少了由于常规经验设置的常数阈值在残差评估过程中所导致的错误报警现象，上述已在20-sim仿真平台得到了验证。

若FSM出现一致，说明故障未全部隔离，还需进一步辨识研究；基于BG的自适应阈值中各项采用了绝对值相加，未考虑参数不确定性间的累加或消除现象，可能会导致阈值过宽，降低了检测的灵敏性，后续需做进一步优化。