用于变压器端部垫块脱落故障识别的时间序列频谱熵稳定度算法

刘云鹏， 周旭东， 王博闻， 严才鑫， 刘嘉硕， 来庭煜

(1.河北省输变电设备安全防御重点实验室(华北电力大学)，河北 保定 071003；2.华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

随着电力系统容量不断提升，变压器作为最重要的变电设备，承担着整个电网的电能转换作用，因此对变压器运行状态的检测和运维工作变得更加重要。研究得知，变压器铁心和绕组在运行时受到硅钢片磁致伸缩和漏磁场的影响产生振动信号，振动信号反映了变压器内部状态信息。当内部发生故障缺陷导致变压器不稳定运行时，会存在不同于工况运行时的噪声信号，靠人耳听声很难辨别，更无法判别变压器的故障类型，一旦发生严重事故，电力系统稳定性和人员安全均造成巨大破坏和威胁。因此，变压器声纹信号的状态监测研究得以迅速发展。

目前，对于变压器声纹监测方法主要有深度学习和特征信号分析法[1，2]。深度学习具有强大的特征学习能力，能够从原始数据中抽离出对象的本质，并完成数据的识别和分类。对于变压器故障识别而言，负载大小，测点位置和变压器连接结构的变化均会导致声纹信号的改变，要实现深度学习的商业模式，需要更完备的样本数据集。特征信号分析法更注重于绕组、铁心的机械状态对振动信号的影响，描述两者之间的底层联系，因此近两年来得到了学者的广泛关注。

油浸变压器振动信号传递到油箱表面的途径主要有两种，一是通过连接组件，二是通过变压器油，并以声波的形式在空气传播[3]。目前，已有学者从现场采集和实验模拟的角度出发，对变压器振动信号特征提取展开研究工作：刘云鹏、王博闻等选取主频、振动熵、50 Hz奇偶次倍频比、奇频比重、高低频比五项典型特征对现场信号进行预警阈值分析[4]；汲胜昌、张凡等构建了绕组两体振动模型，推导出了绕组多倍频振动产生条件，为变压器绕组故障诊断和抗短路能力设计提供参考依据[5，6]；马宏忠等以100 Hz为分析对象，有限元分析了变压器振动信号随预紧力变化规律，达到判断绕组松动程度的目的[7]；王丰华等从垫块非线性角度出发得到绕组正常和松动状态下振动特性，找到绕组松动程度与振动信号中100 Hz倍频分量之间的关联关系[8]。现有关于绕组机械特性和频谱的研究都是基于稳态振动信号，对于不稳定信号而言，频谱分布和幅值大小随时间序列变化较大，因此需要一种新的方法对信号稳定程度进行判别。

本文从某变压器绕组端部垫块脱落故障出发，首先以“质量-弹簧-阻尼”模型[9]为基础分析了端部垫块脱落状态下绕组振动模式随时间序列发展过程，发现传统信号特征提取方法并不适用于信号瞬态的情况。因此，本文构建了一种时间序列频谱熵信号稳定度算法，描述振动信号在动态变化时声纹时频谱的混乱程度。为了验证算法识别端部垫块脱落故障的可靠性，计算河北省电力有限公司管辖的24座500 kV超高压、1 000 kV特高压变电站共162台变压器的声纹数据集和190组实验条件下铁心松动故障声纹数据集的稳定度，划定两种运行状态下的稳定度阈值范围。端部垫块脱落案例的稳定度在阈值范围之外，从而完成该故障的声纹识别工作。

1 绕组端部垫块脱落振动故障分析

1.1 绕组振动分析

变压器绕组是由绝缘圆导线或扁导线绕制而成，构成变压器的磁路部分，其振动是由线饼受到电磁力的作用而产生的，绕组中流通的交流电流形成空间磁场，载流导体在空间磁场受到电磁力的作用，故绕组产生受迫振动[10]。如果绕组发生变形、位移或者崩塌，线饼之间的压紧力不够从而使绕组安匝不平衡加剧，产生的漏磁造成轴向力加大，从而使绕组振动加剧。

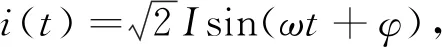
fk(t)=Fk[1-cos(2ωt+2φ)]

(1)

式中：ω为电流角频率，φ为电流相位角。可以证明线圈上的电磁力与电流的平方成正比。

绕组所受到的电磁力在实际工程应用中分解为轴向力和径向力两个分量，垫块脱落故障致使绕组压紧力不足，主要影响轴向电磁力大小。本文只分析轴向电磁力对振动的影响，表达式为

(2)

式中：by为绕组轴向所受电磁力系数；Im为变压器负载电流的最大幅值。

根据绕组的结构特点，可以把单层线圈等效为一个集中的质量块，将绝缘垫片等效为一个弹性元件，浸泡在绝缘油中的绕组受到轴向电动力的作用时的受迫振动实际上是线饼与绝缘垫块、铁轭夹件以及绝缘油相互作用的结果，因此绕组受迫振动被等效为“质量-弹簧-阻尼”的动态等效模型，该模型能够较好地表示绕组的固有振动特性，如图1(a)所示。

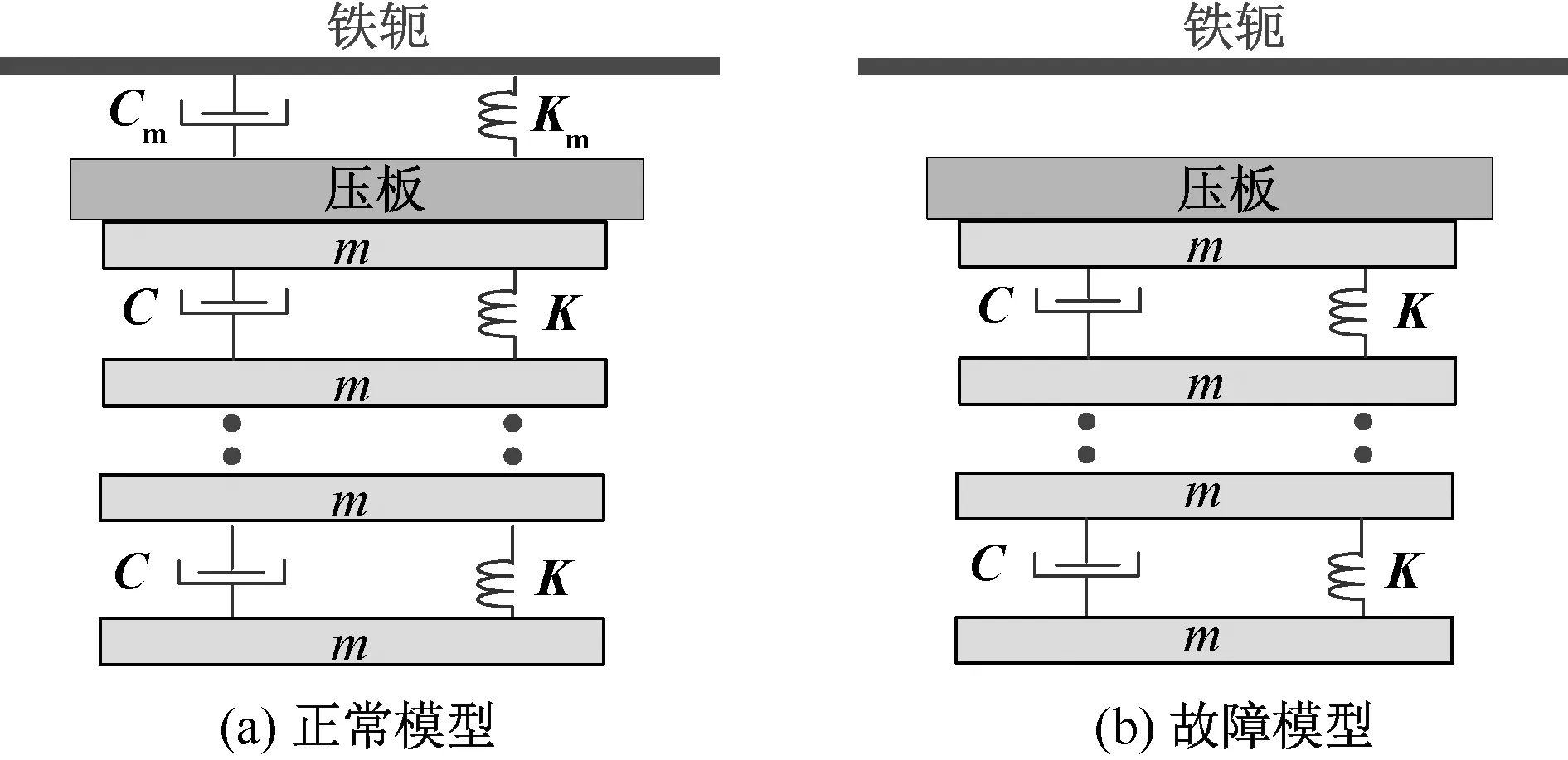
图1 “质量-弹簧-阻尼”等效模型

根据达朗贝尔原理(D.Alembert principle)，线圈单元的动力学方程表示为

(3)

式中：m为线圈单元质量；c为阻尼系数；k为弹簧的弹性系数；xn为第n个单元线圈相对于本身原先位置的位移；Fy为轴向电动力。

本文为了更深入地探究端部垫块脱落情况下绕组的振动响应，将顶层线圈简化为一个单自由度系统[11]。此外，弹簧被看成一个线性系统，工况下与线圈质量相互平衡，为方便计算，将(2)式电动力简化为外部激励Fy0与两倍电网频率的余弦函数相乘的形式，顶层线圈的动力学方程表示为

(4)

根据常微分方程理论，该非齐次线性方程的通解由齐次方程的通解和非齐次方程的特解组成。已知绕组无阻尼振动下的固有频率ω0及相对阻尼系数ζ分别表示为[12]

(5)

则齐次方程的通解可以写成：

(6)

列出其特征方程，得到绕组阻尼振动的特征根。在不考虑电动力的作用下，绕组呈欠阻尼振动，振动幅值表示为

A(t)=e-ζω0t(c1cosωdt+c2sinωdt)

(7)

式中：ωd表示绕组有阻尼固有频率，c1和c2是由绕组初始条件决定的。

通解描述了系统的暂态过程，式(7)表明绕组做振幅逐渐衰减的阻尼振动。考虑非齐次方程特解的情况，首先引入变量S：

(8)

式中：ωF表示绕组受到外部激励的频率，由于电动力为2倍的电网频率，故ωF为固定值100 Hz。

通过数学变换得到振幅放大因子β(s)和相位差θ(s)的表达式：

(9)

最终得到顶层线圈在电动力作用下绕组受迫振动的振幅表达式为

(10)

根据电动力激励下绕组产生受迫振动的响应分析，可知顶层绕组振动幅值呈周期性变化规律，振动频率为100 Hz，在外部激励不变的情况下，振幅x(t)收受到振幅放大因子β(s)的影响。

1.2 端部垫块脱落振动分析

1.1小节研究了工况下绕组振动幅值的数学表达式及影响因素，本小节将从某变电站端部垫块脱落故障出发，理论分析该状态下振动幅值x(t)的变化情况。油浸变压器在拆解之后的现场图如图2所示。

图2 变压器绕组端部垫块脱落现场图

变压器在正常运行时，顶层线圈上放置绝缘压板，为提升预紧力在压板与上铁轭之间加垫了绝缘垫块，脱落时压板与上铁轭之间形成一个很小的缝隙。考虑到绝缘压板系木质结构，密度较小，故在数学分析时不考虑压板的质量，该故障状态下线饼的动态等效模型如图1(b)所示。

线饼之间的绝缘垫块是一种非线性材料，刚度随着预紧力的变化发生改变。文献[14]通过大量实验，认为绝缘垫块所受应力与弹性模量之间的关系表示为

(11)

式中：σ、ε分别表示绝缘垫块的应力和应变；ɑ=1.05×103kg/cm2，b=1.75×104kg/cm2；A为绝缘垫块与线饼的接触面积；h为绝缘垫块高度。

由于变压器发生端部垫块脱落故障，垫块与线饼的接触面积为A为零，导致垫块弹性系数km减小。式(5)中固有振动频率ω0减少，在电网频率不变时，式(8)中变量S增大，根据图3[13]中的响应曲线可以判断β(s)不断增大，式(10)中顶层线圈的振动呈过阻尼振动模式，幅值增大。考虑到绕组压板为非线性材料，与铁轭产生非弹性碰撞，绕组振动幅值减小，并重新积蓄能量，循环往复。

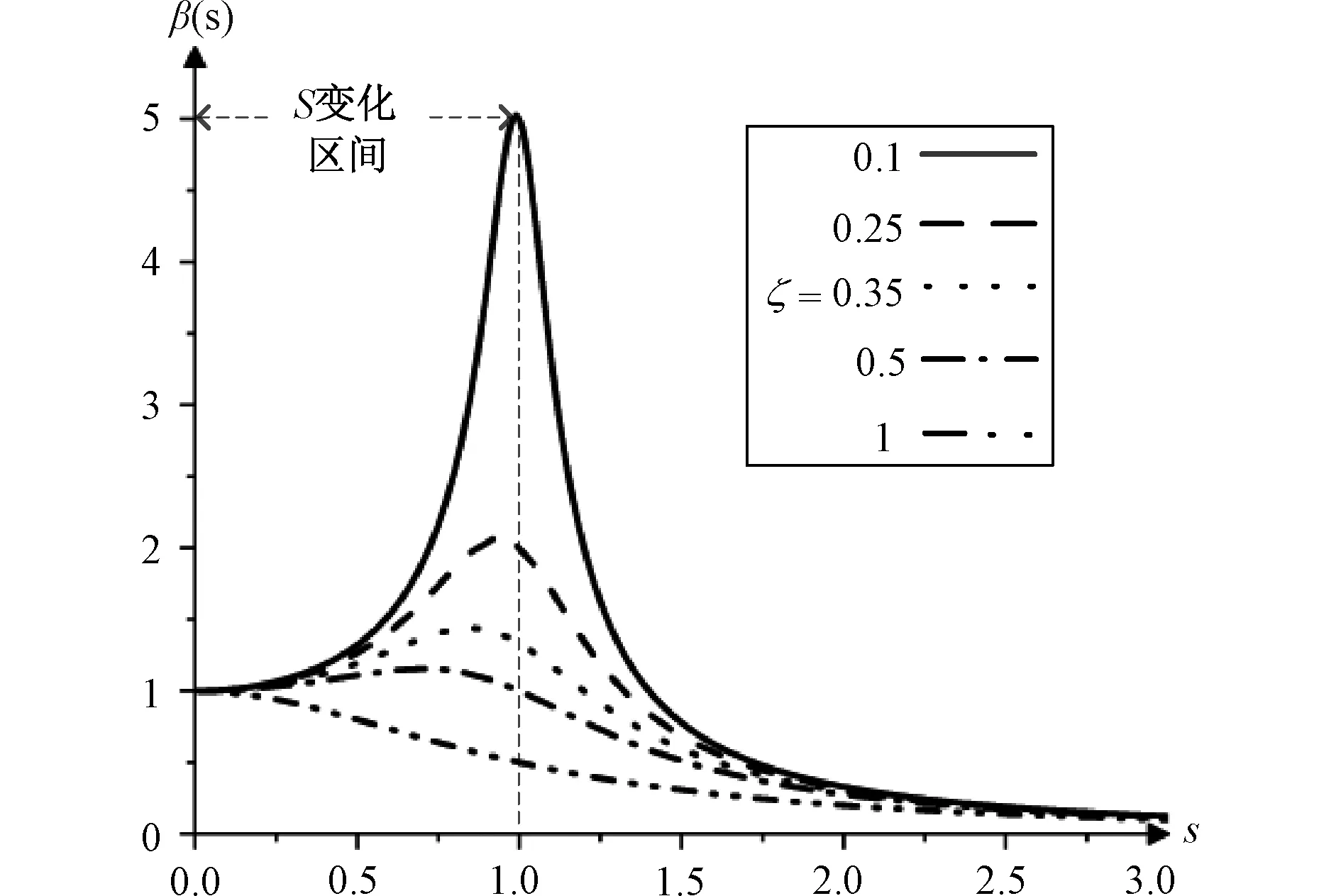
图3 振幅放大因子稳态响应曲线

为验证数学模型，利用文献[15]中变压器二维模型参数计算得到绕组振动的固有频率范围和振幅放大因子大小，假设现场压板与铁轭之间的空隙为0.01 m，得到顶层绕组振幅随时间的变化规律如图4所示。

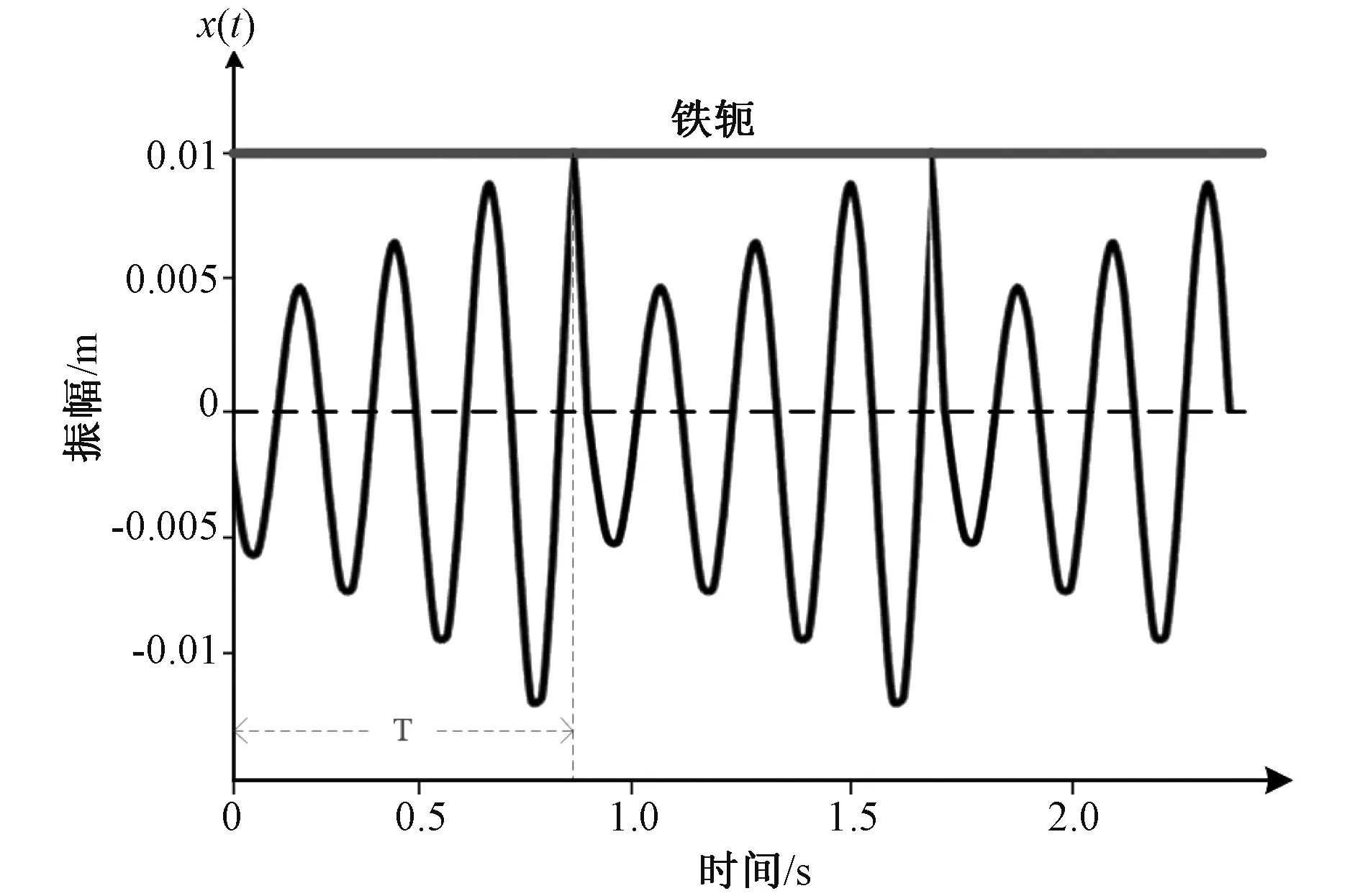
图4 绕组振幅变化规律

综上，端部垫块脱落故障导致线饼呈过阻尼振动，振幅增加并与铁轭反复发生碰撞，要实现该类故障的识别，要利用其动态变化的特点，为后文声学指纹稳定度判别提供理论依据。

2 声纹信号处理与压缩感知

本节将对端部垫块脱落故障现场采集的声纹信号进行频谱变换和特征提取。首先将时域信号转换为声纹时频谱图，其次构建24个Mel滤波器，将声纹时频谱转化为Mel时频谱，实现声纹的压缩感知。

2.1 声纹信号处理

截取4 s垫块脱落故障下的变压器声纹信号，考虑到声纹信号在在短时间内平稳的特性，对信号进行分帧、加窗，对每一帧信号计算短时傅里叶变换(Short-time Fourier transform，STFT)[16]。信号的采样频率fs=48 000 Hz，设置帧长和帧移分别为采样频率的0.1倍和0.02倍，频谱分辨率f0=10 Hz。为了有效减少信号频谱泄漏和信号失真的情况，利用Blackman-Harris窗函数对帧长信号进行处理，Blackman-Harris窗公式为

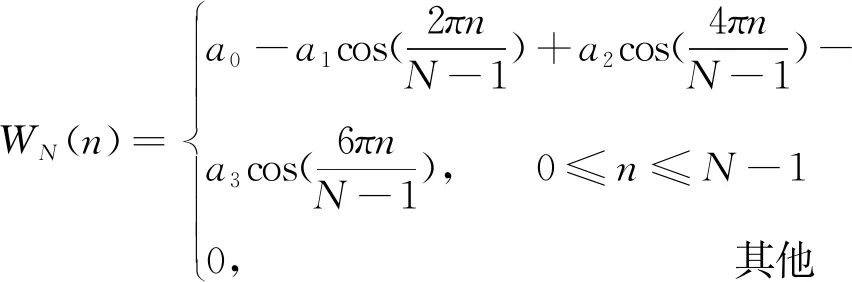
式中:a0=0.358 75，a1=0.488 29，a2=0.142 8，a3=0.011 68;N为信号长度。

时域信号转化为声纹时频谱信号，并按照时间维度堆叠成的声纹时频谱图，该图像包含信号三种信息：时间、频率和信号强度，由此可见声纹时频谱图是一种集合了时域频域及图像特性的特殊数据表示方式。本文只考虑5 000 Hz范围内的频谱分量。

经过对时域信号的预处理和短时傅里叶变换后，得到的声纹信号时频谱矩阵大小为[501×196]，其中501描述了频谱从0～5 000 Hz频率范围内的信号频谱，196表示在信号在4 s内拆分成196个时段，每个时段持续时间为0.02 s，矩阵的数值表示声纹信号对应频谱和时间的强度，在这里用dB表示。信号的声纹时频谱如图5(a)所示。此外，对时域信号进行快速傅里叶变换得到50 Hz及其倍频的频谱分布情况如图5(b)所示。

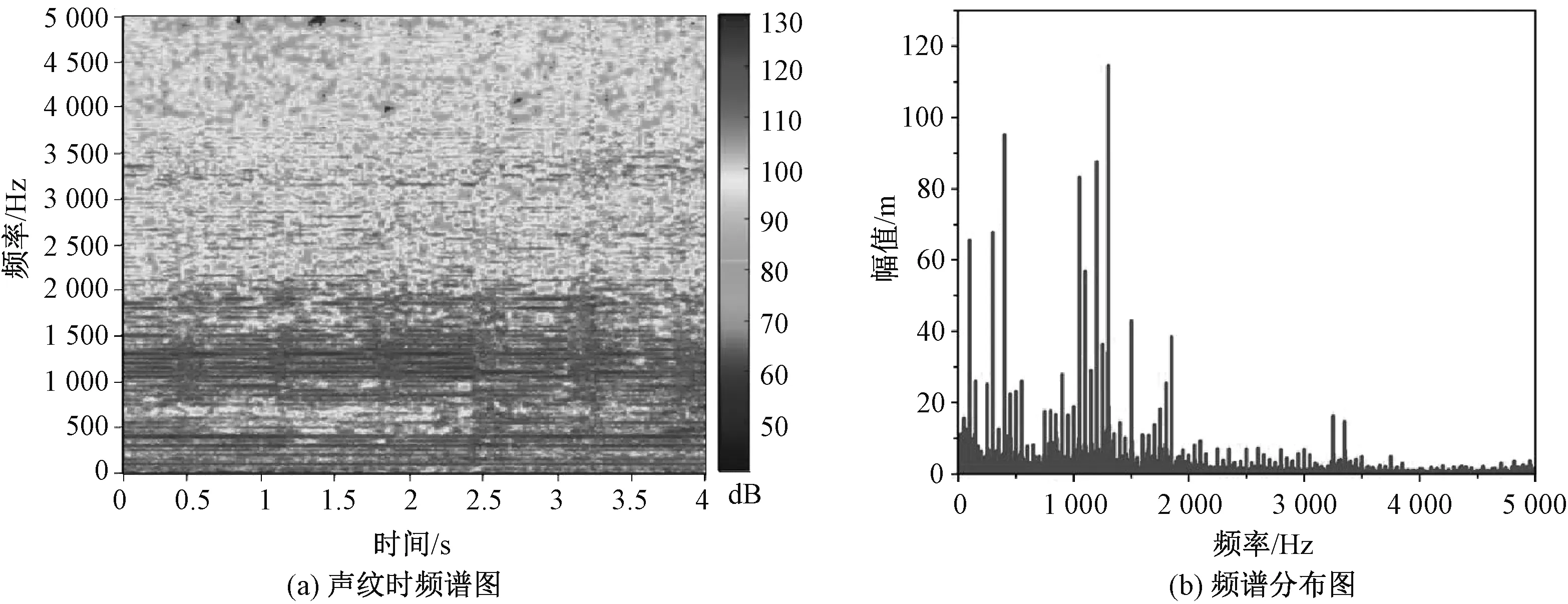
图5 声纹时频谱图和频谱分布图

图5分析可知垫块脱落状态下的频谱分布区间较广，且能量主要集中在0～500 Hz以及1 000～1 500 Hz范围内，主频分量为1 300 Hz。声纹呈波纹状分布特点，为瞬态分布特征。

2.2 声纹压缩感知

考虑到人耳对于可听声范围内标度的感知是非线性的，期望能获得更好的语音特性之余，对信号进行频谱压缩，为声纹在线监测提供便利[17]。本文引入Mel滤波器组(Mel filter group)对声纹时频谱信号降维处理，降低干扰频段的权重。实际频率与Mel感知频率之间的对应关系表示为[18]

Mel(k)=2 595lg(1+f/700)

(13)

Mel-1(f)=700×(10(1+k/2 595)-1)

(14)

式中：f为正常标度的频率，0≤f≤5 000；k为Mel感知频率，单位均为Hz。

(15)

式中：p=2×{f(m)-f(m-1)}，q=2×{f(m+1)-f(m)}，m表示每个滤波器，0≤m<24，f(m)表示滤波器组的中心频率，表达式为

(16)

式中：fmax，fmin分别表示滤波器范围的最大值和最小值，本文取fmax=5 000 Hz，fmin=0。

将式(15)中传递函数进行归一化处理，得到Hm的相对幅值如图6所示。

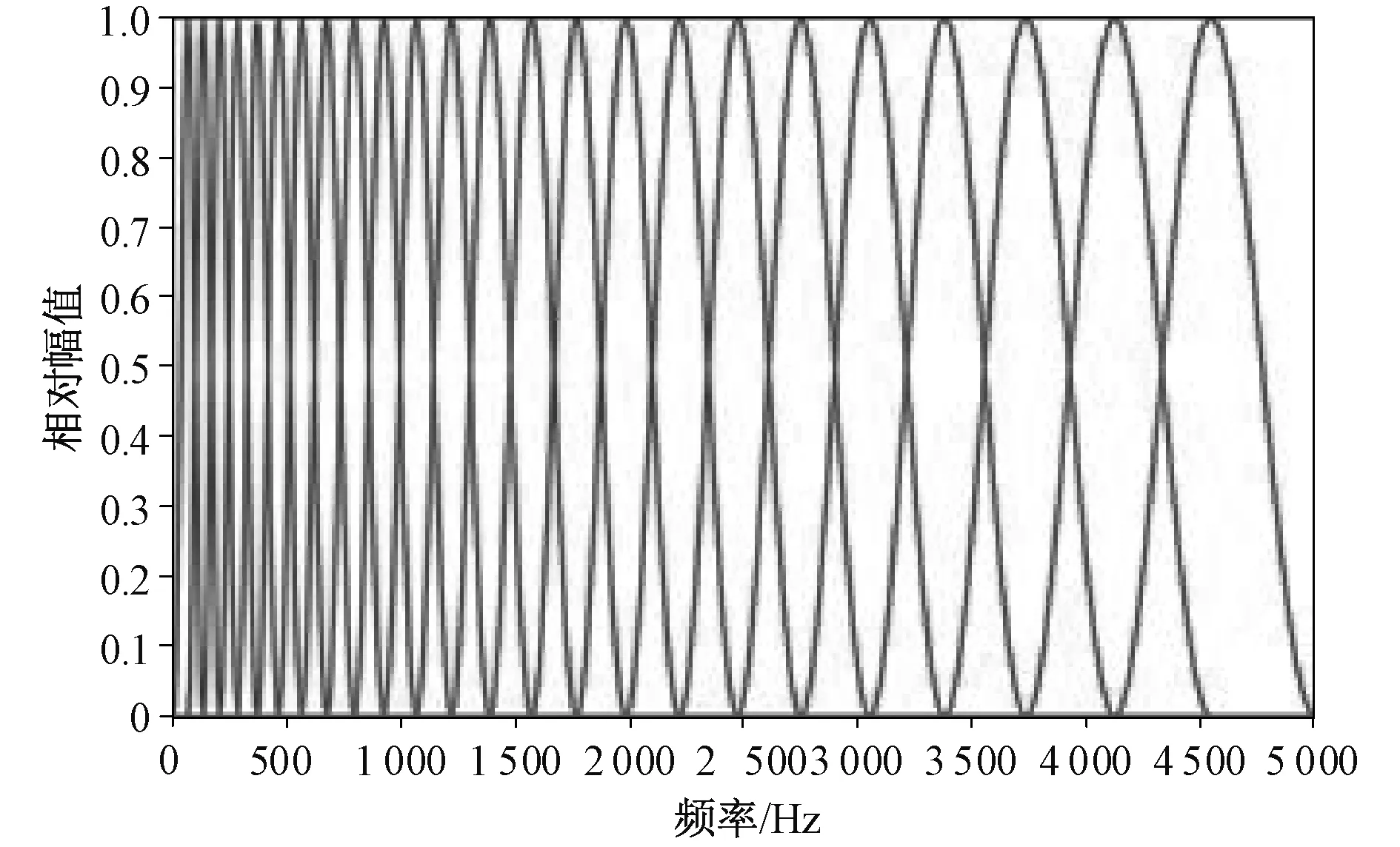
图6 24个Mel滤波器传递函数

图6中设计的Mel滤波器组在5 000 Hz频率范围内传递函数矩阵大小为[24×501]，将Mel滤波传递函数矩阵与声纹信号时频谱矩阵相乘，最终得到Mel标度下的时频谱矩阵。图7描述了垫块脱落声纹时频谱矩阵转化为Mel时频谱矩阵的具体流程。

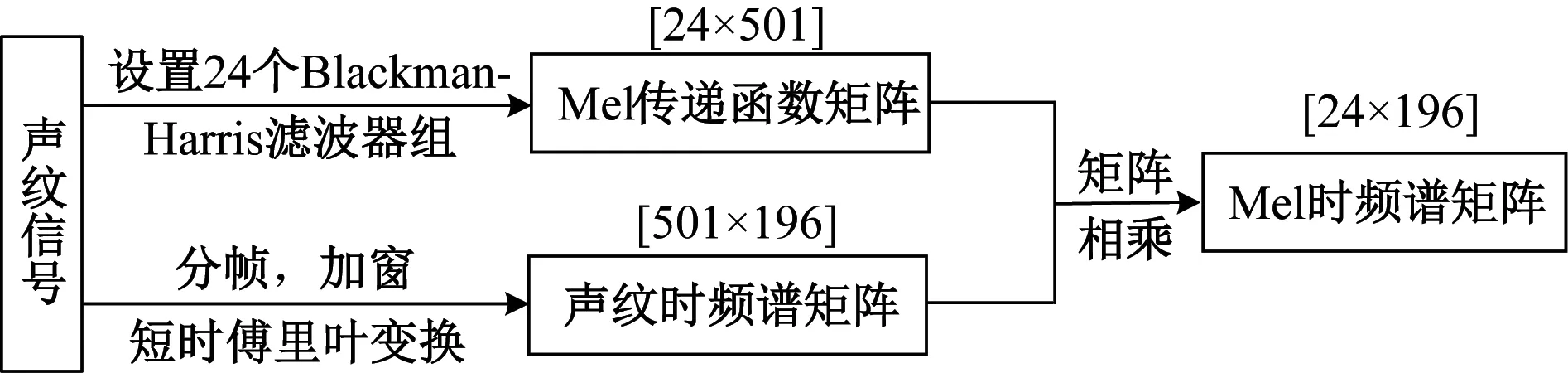
图7 Mel时频谱计算流程

声纹时频谱矩阵转化成Mel时频谱矩阵，在保留原有信号特征的同时消除了噪声信号的影响，矩阵大小由原来的[501×196]压缩成[24×196]，下降了一个数量级，降低了后续稳定度计算的运算复杂度，更加高效地处理数据样本。

3 时间序列频谱熵稳定度算法

本节考虑端部垫块脱落声纹瞬态分布特点，引入了一种利用时间序列频谱熵计算稳定度的算法来描述声纹信号频谱的混乱程度。以下为稳定度计算流程。

3.1 稳定度计算流程

首先，提取Mel时频谱矩阵的每一帧向量，该列向量长度[24×1]。其次，对相邻帧向量作频谱差，计算频谱差向量的时间序列谱熵值，按照时间排列成一个新的时间序列频谱熵横向量[1×195]。最后，计算时间序列频谱熵的均方根值，得到整个声纹时频谱的稳定度。计算方法如图8所示。

图8 时间序列稳定度计算方法

3.2 稳定度表达式

本小节介绍时间序列频谱熵稳定度的计算表达式。

1.保持良好的精神状态。党员领导干部是上级决策部署的执行者，是本单位、本部门干部风气和干事氛围的影响者和引领者。其精神状态如何，直接影响到员工的工作状态，反映出队伍的作风形象，决定着工作的效率质量，关乎事业的起伏兴衰。要始终保持对工作的热情、激情，要有一种不怕困难、不怕挫折的勇气，一种敢闯敢干、敢为人先的锐气，一种勇往直前、勇立潮头的豪气，切实坚定理想信念，不断提升思想境界和工作水平。

3.2.1 Mel时频谱相邻帧向量频谱差

计算Mel标度下相邻帧向量频谱差值，并随时间排列为一个新的频谱差向量：

Xi=xi+1-xi,(1≤i≤T-1)

(17)

式中：T表示将时频谱帧向量数，本文算例中取196。

3.2.2 时间序列频谱熵算法

计算Mel时频谱熵特征矢量[19]：

(18)

式中：M表示Mel时频谱谱线数，本文算例中取24，sgn函数公式如下：

(19)

然后，对特征矢量进行归一化：

(20)

3.2.3 稳定度计算

计算频谱熵序列Z的均方根得到稳定度：

(21)

该算法表征了声纹信号频谱能量集中度的变化情况。当信号瞬态分布时，相邻频谱序列的频谱熵值构成的特征向量相差越大，其自相关性越弱，计算得到的K值越小。相反，K值越接近1则表示信号相关性越强，稳定度越高。因此，可以根据K值的大小判断信号的稳定度。

4 数据集稳定度计算与算法对比

本节计算端部垫块脱落故障稳定度K值，划定现场工况数据集和铁心松动数据集K值阈值范围，达到该故障在变压器不同运行状态时的辨识效果。为了体现算法的有效性，采用传统的距离测度作对比验证。

4.1 数据集稳定度计算

分别对2种不同运行状态下的变压器声纹数据集和端部垫块脱落故障进行稳定度计算，稳定度算法除时间序列频谱熵外，采用欧氏距离和余弦距离作对比。

第1组数据集(现场工况)为河北省24座500 kV变电站共162台变压器2个时段共324组声纹数据；第2组数据集(铁心松动)为试验状态下采集的190组铁心松动故障声纹数据。端部垫块脱落与2组数据集的声纹时频谱图和Mel时频谱图对比如图9所示。与端部垫块脱落故障相比，变压器工况运行和铁心松动故障除了频谱分布有差异之外，时频谱呈现稳态分布特征。

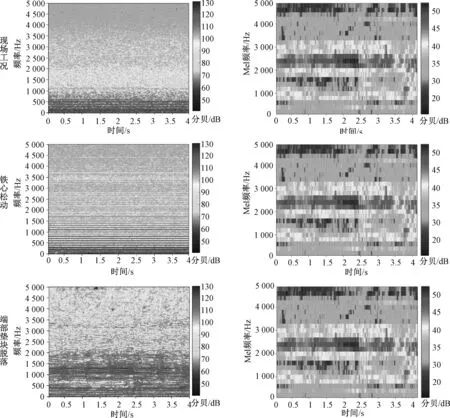
图9 3种运行状态时频谱分布图

两数据集的稳定度分布统计结果如表1所示。可以看出，欧氏距离、余弦距离和时间序列频谱熵满足正态分布或对数正态分布，变压器工况运行状态下由于自相关距离样本集中在零点附近，分布状态呈指数分布规律。

表1 3种算法稳定度分布状态与分布参数

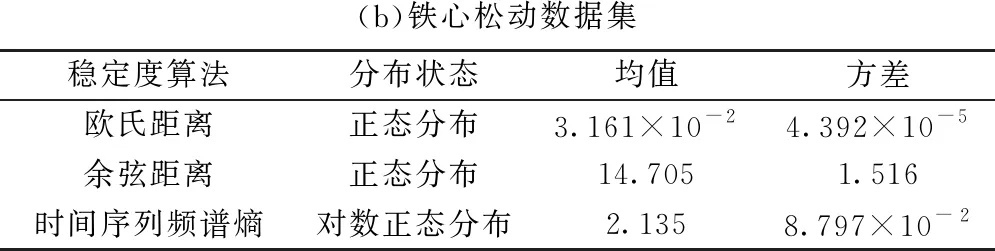
(b)铁心松动数据集稳定度算法分布状态均值方差欧氏距离正态分布3.161×10-24.392×10-5余弦距离正态分布14.7051.516时间序列频谱熵对数正态分布2.1358.797×10-2

4.2 算法对比

为比较3种稳定度算法在垫块脱落故障识别方面的有效性，本文对各稳定度计算结果进行横向对比，结果如图10所示。

图10 变压器工况、铁心松动、端部垫块脱落运行状态下稳定度分布情况

(1)欧氏距离稳定度：现场数据集的稳定度分布范围较广，其中1%～99%分位线数值为4.01×10-3～8.039×10-2，相比而言，铁心松动故障稳定度分布总体趋势增加不明显，其中1%～99%分位线数值为1.707×10-2～4.886×10-2，端部垫块脱落稳定度数值为5.25×10-2，因此该算法计算的稳定度无法区分端部垫块脱落故障。

(2)余弦距离稳定度：该算法下的现场数据集和铁心松动数据集有明显差异，稳定度分布范围在1%～99%区间分别是3.461～10.303与11.659～17.715，但端部垫块脱落稳定度在铁心松动稳定度区间内，其数值为14.777 3，因此该算法无法区分端部垫块脱落故障。

(3)时间序列频谱熵稳定度：该算法从频谱信号能量的分布均匀程度来计算稳定度，稳定度数值为1.252 7，低于两类数据集的1%分位线。现场和铁心松动数据集稳定度计算结果1%～99%分位线分别为1.532 1～3.113 0和1.359 4～2.899，可以看出，该方法在区分端部垫块脱落故障方面具有良好效果。

综上，与欧氏距离和余弦距离相比，时间序列频谱熵稳定度算法能保证端部垫块脱落故障的K值在两数据集1%～99%分位线之外，从而实现该类故障识别的效果。

5 结 论

本文以变压器垫块脱落故障为出发点，从机理和声纹的角度分析该故障的振动过程，针对该故障声纹时频谱信号混乱程度较高，引入了稳定度计算公式，为变压器稳态运行和非稳态运行时的判别提供了参考价值。本文所得的主要结论如下：

(1)针对发生端部垫块脱落故障的变压器声纹信号的分析发现变压器工作模态并不稳定，建立绕组“质量-弹簧-阻尼”等效模型，利用电磁-振动力学分析理论模型分析了变压器状态变化过程，解释了该模态下绕组的振动过程；

(2)采用Mel滤波器组对声纹时频谱信号进行数据压缩感知，在保留信号原有特征的同时，将数据量减小了一个数量级，为后续的特征提取和稳定度计算提供支撑；

(3)针对目前常用的特征提取方法，还没有用来描述信号混乱程度的评价方案。本文利用时间标度下频谱熵算法引入了稳定度计算思路，与传统的距离测度直接计算稳定度相比，更能区分时频谱信号的混乱程度，并实现了垫块脱落故障的识别工作。