基于单类支持向量机的工业控制系统入侵检测

张子迎， 潘思辰， 王宇华

(1.嘉应学院 计算机学院，广东 梅州 514015； 2.哈尔滨工程大学 计算机与科学技术学院，黑龙江 哈尔滨 150001)

入侵检测是工业控制系统(industrial control system，ICS)安全防御中关键的一环，通过对系统中关键数据的收集分析，实时检测出系统内外的异常行为并采取相应的保护措施，可有效地增强系统的攻击检测及预警能力。

单类支持向量机(one class support vector machine，OCSVM)[1]因其特有的优势，成为入侵检测中最为常用的方法之一，并已经取得了一定的成果。Kim等[2]首先基于C4.5决策树算法对数据进行分解，然后构造多个OCSVM模型对分解后的数据集进行训练，该方法可以利用异常和正常这2种行为信息，但是忽略了各数据集合之间的联系；Nguyen等[3]针对高维数据集提出了一种基于自动编码器的单类支持向量机的入侵检测方法，利用随机梯度下降来获得端到端的训练，检测性能明显增强但是训练速度较慢。秦济韬[4]首先利用变分自编码器(variational auto-encoder,VAE)对样本进行低维编码并将模型重构误差输入到分类器中，然后利用随机傅里叶特征(random Fourier features,RFF)和Hinge loss目标函数对OCSVM进行优化。该方法对异常样本具有较好的检测能力，但是对时序情况下和非结构化数据的检测效果不佳。王华忠等[5-6]在主成分分析(principle component analysis，PCA)方法对入侵数据进行降维的基础上，利用粒子群算法对支持向量机参数进行优化，以获得较优的入侵检测模型。但上述研究没有考虑工业控制系统中数据纬度高、非线性等特点及粒子群算法容易陷入局部极小值等问题。

针对以上问题，本文在核主成分分析(kernel principle component analysis，KPCA)的基础上引入Fisher-Score，综合考虑样本的类别信息和特征信息总量，实现对工业数据的特征提取；其次采用分层协同免疫粒子群(hierarchical collaborative immune particle swarm optimization，HCIPSO)算法对OCSVM参数进行寻优，克服了基本粒子群易早熟陷入局部收敛等问题；最后基于优化后的OCSVM算法构建入侵检测模型，应用密西西比大学公开的工控入侵检测数据集进行仿真对比实验验证。

1 工业数据的特征提取

本文采用了一种基于Fisher特征选择的改进KPCA方法(kernel principal component analysis method based on fisher feature improved selection,FKPCA)，首先基于Fisher-Score筛选出最利于分类的特征，再对特征进行KPCA降维，实现数据的特征提取。

将Fisher-Score引入KPCA，根据类内和类间聚散度这2项指标来计算特征的类别信息量，提取特征和类别空间中的非线性信息[7]，并选择对分类贡献度大的特征建立新的数据子集进行核主成分分析，具体实现步骤如下：

1) 输入工业数据集[x1,x2,…,xN],其中xi=[x1ix2i…xLi]T，xi∈R，i=1,2,…,N，L为样本总个数，N为数据特征维数。可将样本划分为e类，每类样本个数li。

2) 计算各特征的Fisher-Score：

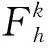
3) 选择类间距离大而类内距离小的特征建立特征子集，将特征按Fk从大到小排序，选择前M个特征建立新的数据集ULxM。

4) 输入新的数据集ULxM；根据核函数K(xi,xj)，计算核函数矩阵K：

K=[Ki,j]L×L=K(xi,xj)=

式中：I为L×L的矩阵，且满足Iij=1/L。

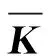
7) 将λ降序排列并计算累积贡献率，选出满足式(1)的前m个非线性主成分：

(1)

8) 计算样本数据的非线性主成分Y,实现工业数据的降维：

选出前m个非线性主成分累计方差贡献率超过90%的特征向量，输出降维后的样本数据YLxm，实现对工业数据的降维。

2 基于FKPCA-HCIPSO-OCSVM的工业控制系统入侵检测

2.1 HCIPSO算法

在OCSVM入侵检测算法中，分类决策函数核参数g和权衡参数v设置不当，会造成模型计算复杂度过大或者过拟合等问题。因此，本文将免疫克隆选择和协同进化策略引入粒子群算法(particle swarm optimization,PSO)，提出一种分层协同免疫粒子群(hierarchical collaborative immune particle swarm optimization，HCIPSO)参数优化算法。该算法模型采用层状结构。普通层各子群的独立搜索和复合进化模式扩大了解空间搜索范围，自适应层种群通过与普通层粒子进行交流快速地向全局最优解靠近,保证了算法的收敛性，精英层种群则进行全局指导，提升整体检索性能，加强信息交流和各种群间协作，增强算法收敛性能。HCIPSO算法流程如图1所示。

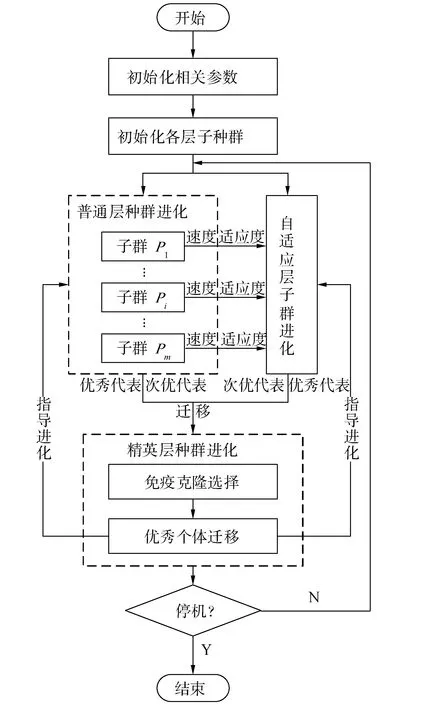
图1 分层协同免疫粒子群算法(HCIPSO)流程图Fig.1 Flow chart of hierarchical collaborative immune particle swarm optimization (HCIPSO)

整个粒子簇由N个在D维搜索空间中移动的粒子构成，粒子i(i=1,2,…,N)的位置和速度为Xi={Xi1,Xi2,…,Xid}、Vi={Vi1,Vi2,…,Vid}，粒子位置为参数最优问题中的一个可行解，通过目标函数计算得到度量该解的适应度值fiti(t)。

2.1.1 普通层免疫粒子群算法

普通层种群Pi(t)=(P1,P2,…,Pi,…,Pm)，位于模型的底层，其中Pi代表第i个普通子种群。普通子种群中粒子速度和位置的更新方式与标准粒子群相同，具体进化步骤如下：

1) 精英保留：根据适应度从大到小对粒子进行排序，选择前k个优秀粒子复制至下一代。

2) 次优变异：在k个精英粒子中随机选择一个粒子和次优的m个粒子执行Cauchy免疫变异操作，将精英粒子的优秀抗体基因注入次优粒子中，具体变异操作为：

Pg(t+1)=Pg(t)-r1(Pg(t)-Ph(t))+

r2CauchyPg(t)

(2)

式中：r1、r2是0～1上的随机数；Pg、Ph分别表示次优粒子和精英粒子；CauchyPg(t)为密度函数。

3) 末位淘汰：选择末位的L个粒子执行初始化操作，增强种群活性。

2.1.2 自适应层免疫粒子群算法

自适应层种群Psa(t)位于模型的中间层，其种群内粒子数量和下层子种群相同。该层种群综合全局的速度和适应度信息自适应地对飞行方向和速度进行调整。粒子的速度更新方式为：

(3)

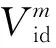
自适应层第i个粒子的位置更新方式为：

(4)

式中：δ1、δ2、δ3为影响因子，并满足δ1+δ2+δ3=1。

2.1.3 精英层免疫粒子群算法

精英层种群Pe(t)=(P1j,P2j,…,Pij,…,Pmj,…,Psaj)位于模型的顶层，其中Pij为第i个子种群的第j个粒子。每一代种群更新之后，在普通层各子群中选取一个最佳粒子，在自适应层中随机选取一个次佳粒子提呈至精英层，采用免疫克隆算子引导精英粒子进行进化，进化完毕则选择优秀个体迁移回普通层和自适应层。进化步骤如下：

1) 将精英层的每个粒子看作是抗体，根据各抗体的亲和度大小对其进行排序并进行免疫克隆操作生成临时种群，克隆倍数Nc与该抗体的亲和度有关。

式中：fi表示粒子的适应度，D表示精英层种群规模，∂表示0～1的克隆系数。

2) 对扩增后的临时种群执行变尺度的高频变异操作，在维持解的多样性的同时实现局部微调，变异算子为：

Pid(t+1)=

ρ(t)=1-r[1-(t/T)]2

(5)

式中：ρ(t)表示变异尺度；T表示总进化代数；r和u(0,1)为0～1随机数。由式(5)可知，对于较小的r，在进化初期λ(k)接近于1，变异能力强；在进化后期λ(k)接近于0，变异强度减弱，实现了对局部范围的精细搜索。

3) 克隆选择，从变异后的群体中选择最优秀的个体进入下一代。

2.1.4 HCIPSO算法执行步骤

HCIPSO算法具体实现步骤如下:

算法HCIPSO

输入：vi和wi;

输出：Wi=[Wi1Wi2…WigWiv…Wid]T。

1)初始化HCIPSO，子群Pi、Psa、Pe，种群规模N，D维空间粒子随机速度Vi=[Vi1Vi2…Vid]T,位置Wi=[Wi1Wi2…Wid]T、及参数ω、δ、∂、c1、r1、c2、r2等；

2)While 未达到终止条件 // 最优解或者最大迭代次数；

IfT≥1 // 迭代次数大于1；

For EachK∈Pido

CalculateVid(t+1)、Wid(t+1)、fiti(t)//更新普通层种群Pi(t)=(P1,…,Pi,…,Pm)各粒子速度和位置；计算粒子适应度值；

If fiti(t) ∉末位Lthen

CalculatePg(t+1) // 按式(2)随机选择一个粒子和次优的m个粒子执行Cauchy免疫变异操作；

Else deletePi(t) // 末位淘汰；

End if

3)For EachK∈Psado

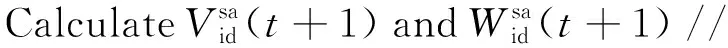
4)For EachK∈Pedo

CalculatePe(t+1) // 各子群的一个最佳和随机一个次佳粒子提呈至精英层，并执行免疫克隆操作实现精英层的种群进化；

5)Calculate fite(t)// 计算精英层粒子的适应度，选取部分优秀粒子迁移回普通层和自适应层；

Else

返回2)

End while

6)输出最优位置和速度。

该方法引入人工免疫思想促使粒子群跳出局部极值点，通过对普通层进行混合免疫操作保证种群的多样性和算法的全局寻优能力；同时自适应层的粒子根据普通层信息进行自适应迭代以增进种群间的信息交流；而精英层进行免疫克隆选择操作可以增强种群的进化速度和算法的寻优性能。因此多群体的协同进化使算法的局部和全局搜索能力得到有效平衡，更加适用于复杂问题。同时，群体间的信息交互和共享可以降低算法的冗余，提高收敛速度。

2.2 FKPCA-HCIPSO-OCSVM入侵检测算法

本文使用FKPCA算法对工控系统的数据进行特征提取，同时引入HCIPSO算法对OCSVM模型的参数进行寻优，在减少检测模型训练时间的同时提升对入侵行为的检测准确度，进一步满足工业控制系统(industrial control system,ICS)对安全防护能力和入侵检测相关指标的要求[8]。FKPCA-HCIPSO-OCSVM入侵检测算法流程如图2所示。

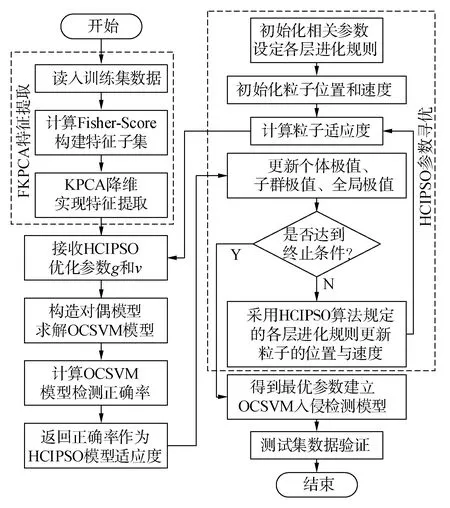
图2 FKPCA-HCIPSO-OCSVM入侵检测流程Fig.2 FKPCA-HCIPSO-OCSVM algorithm flow chart

算法分为4个阶段:

1) 数据预处理：首先利用Fisher-Score对原始工业数据集进行特征选择以构建新的特征子集，然后采用KPCA方法对该子集进行降维，建立新的入侵检测数据集。

2) OCSVM模型建立：利用特征提取后的数据集建立OCSVM入侵检测训练模型，确定入侵检测模型的验证规则。

3) OCSVM参数寻优：初始化粒子群，利用粒子群传递的参数g和v构造OCSVM模型并进行训练，其中各粒子的位置和速度为Xi=[xigxiv]、Vi=[vigviv]，代表入侵检测模型中需要进行寻优的2个参数g和v，设置参数范围[Xmin,Xmax]、[Vmin,Vmax]，然后返回OCSVM模型的入侵检测准确率作为粒子适应度，采用HCIPSO算法对粒子群进行进化更新，获得最优参数，构建最终的OCSVM入侵检测模型。

4) OCSVM模型验证：首先采取与训练集相同的方法对测试集进行预处理，然后利用上述训练好的OCSVM入侵检测模型对该数据集进行检测，通过评价指标验证该模型的入侵检测效果。

3 实验及结果分析

3.1 数据集与评价指标

本文采用密西西比大学公开的基于Modbus Tcp协议的工控入侵检测数据集，该数据集包含反映网络流量、过程控制和过程测量功能的特征[9]；主要分为：恶意响应注入攻击、恶意命令注入攻击、拒绝服务攻击、侦察攻击[10]4类。将“Nomal”类的正常数据样本标记为+1类，其余类别均当作异常数据样本标记为-1类。随机选取6 000条样本，包括4 800条由正常数据样本构成的训练集和1 200条由正常数据样本和异常数据样本构成的测试集，通过实验验证该方法的性能。同时，将通过准确率(accuracy,ACC)、精确率(Precision)、误报率(false negative rate,FNR)、异常样本精确率(true negative rate,TNR)、漏报率FPR和F1分数这几种评价指标来衡量该模型的检测性能。

3.2 特征提取与参数优化

3.2.1 FKPCA特征提取

随机选取2 000条既有正常数据又有异常数据的样本集，对样本集进行特征选择，计算每个特征的Fisher-Score并从大到小排列，采用基本OCSVM作为分类器，依次选取特征训练模型并计算特征综合贡献度。

如图3所示，添加至第15个特征时，综合贡献度达到峰值，此时入侵检测模型性能最好。后续特征对模型的影响很小，说明其相关性较差且无益于后续入侵检测的分类识别，因此选择前15个特征为最终的特征子集。

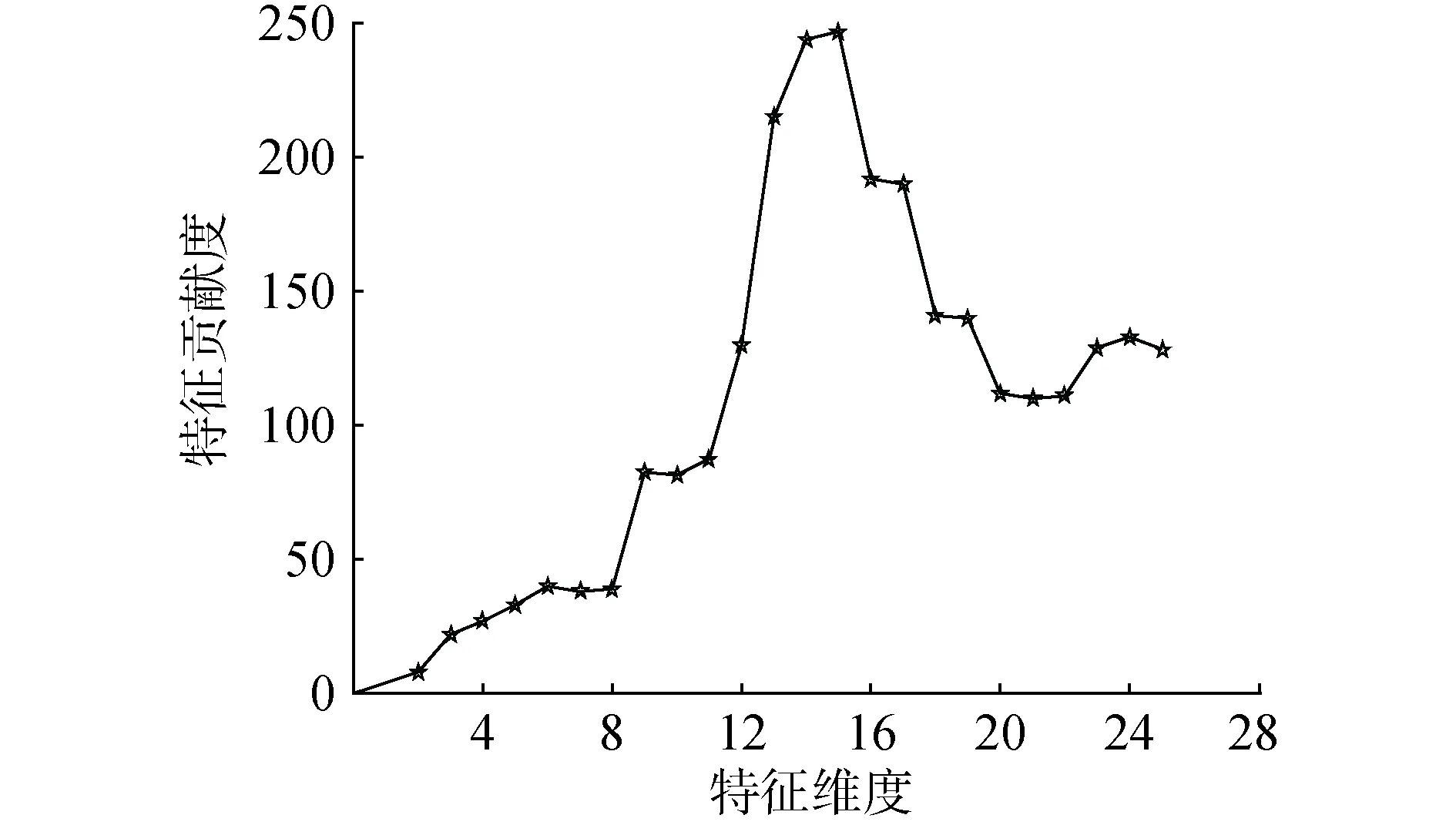
图3 特征综合贡献度变化曲线Fig.3 Variation curve of feature comprehensive contribution

经过Fisher特征选择之后，采用KPCA方法对新特征子集进行降维。降维结果如图4所示，根据特征值累积贡献率超过90%的标准，选取前8维主成分信息组成新数据集。

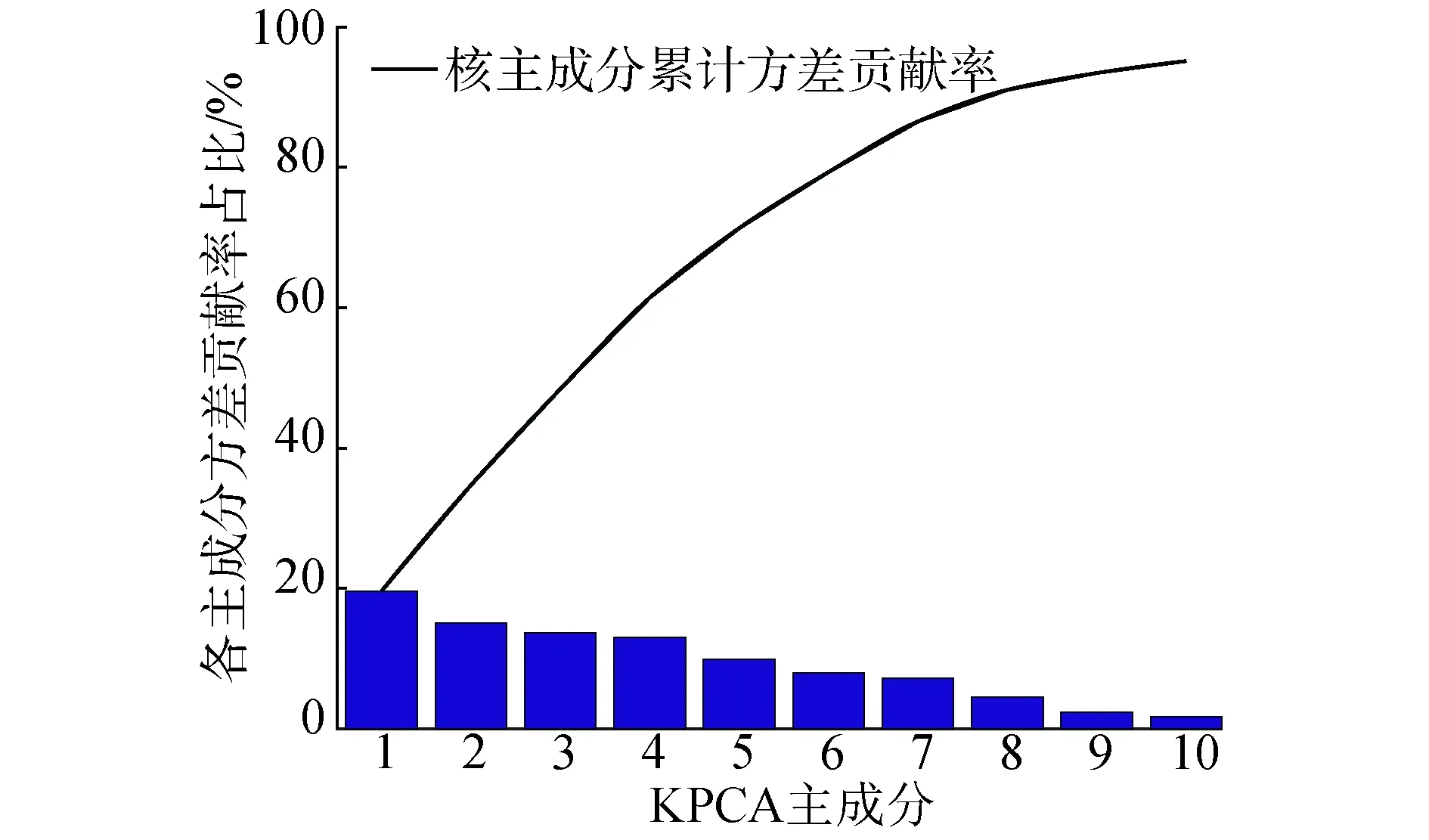
图4 KPCA降维结果Fig.4 KPCA dimensionality reduction results

而表1中，基于FKPCA的入侵检测算法在3个评价指标上有不错的表现，不仅提升了识别准确率、降低了异常样本漏报率而且缩短了训练时间。

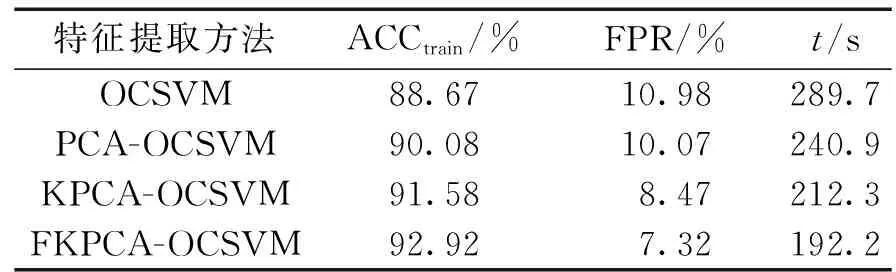
表1 特征提取效果对比Table 1 Comparison of feature extraction effects

3.2.2 HCIPSO参数优化

为了验证HCIPSO参数优化方法对OCSVM入侵检测模型的优化效果，本文将HCIPSO、免疫粒子群(immune particle swarm optimization,IPSO)、粒子群(genetic algorithm,PSO)、遗传算法(GA)对OCSVM参数寻优的结果进行比较，c1=1.7，c2=1.5，ω=0.9，其中迭代次数为50。

HCIPSO普通子群数为3，子群规模为10，其余粒子群算法种群规模为50，GA算法染色体数量为50。经过多次仿真实验，各代的训练适应度迭代曲线如图5，模型的训练时间和训练准确率如表2。

由图5和表2可以看出HCIPSO算法对OCSVM的寻优效果最好，准确率达到了98.86%;PSO的优化效果最差，只有94.58%；IPSO的收敛速度最快，12代左右就能达到最优值；HCIPSO仅次于IPSO，在第15代左右收敛至最优；GA收敛速度最慢但准确度略高于PSO。从图5中可以看出，结合了人工免疫思想的PSO优化算法全局寻优能力有所提升，HCIPSO算法虽然比IPSO算法的收敛速度稍慢一些，但在整体寻优效果上仍具有一定的优势。同时，相比于PSO算法，IPSO和HCIPSO的训练时间有所增长，这是由其在寻优过程中的选择、克隆和变异等操作引起的。但是其训练时间分别只增长了5.4 s和8.9 s，并不会影响检测模型的实际应用。

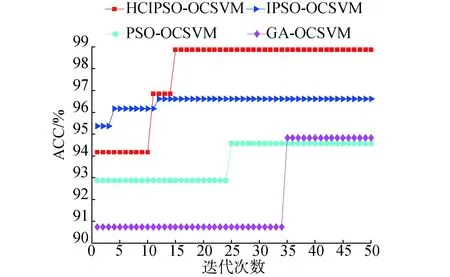
图5 不同算法优化OCSVM的训练准确率对比Fig.5 Comparison of training accuracy of OCSVM optimized by different algorithms

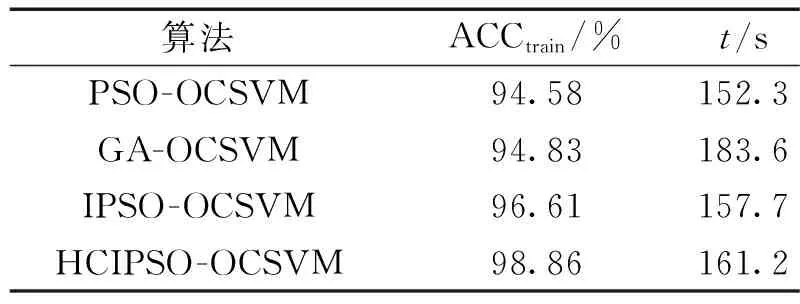
表2 优化算法训练时间和训练准确率对比Table 2 Comparison of optimization algorithm training time and training

3.3 测试结果分析

本文使用1 200组测试数据集来测试训练所得到的OCSVM模型，因为实验数据集为不平衡数据集，除ACC和Precision以外，还使用误报率FNR、漏报率FPR及F1指标来综合评价算法的检测识别性能，具体测试结果如表3。

由表3可知，使用HCIPSO优化的OCSVM入侵检测模型的检测准确率最高，达到了98.58%，相比于训练集准确率只减少了0.28%，而GA算法测试集检测准确率比训练集明显下降。HCIPSO-OCSVM的精确率达到98.82%。同时，其漏报率和误报率明显低于其他算法优化后的模型。另外，从整体来看，本文算法的F1-score要比其他方法更高，对工控网络数据更有效，有一定的实用价值。

表3 各优化算法入侵检测结果对比Table 3 Comparison of intrusion detection results of various optimization algorithms

以上指标大多是对正常样本的识别情况进行评价，图6展示出模型对异常样本的识别能力和识别精确度。

如图6(a)所示，黄色面积越大，代表了实际识别出异常样本的程度越高；如图6(b)所示，黄色面积越大，代表在被识别为异常的样本中，真实的异常样本所占比例越大。

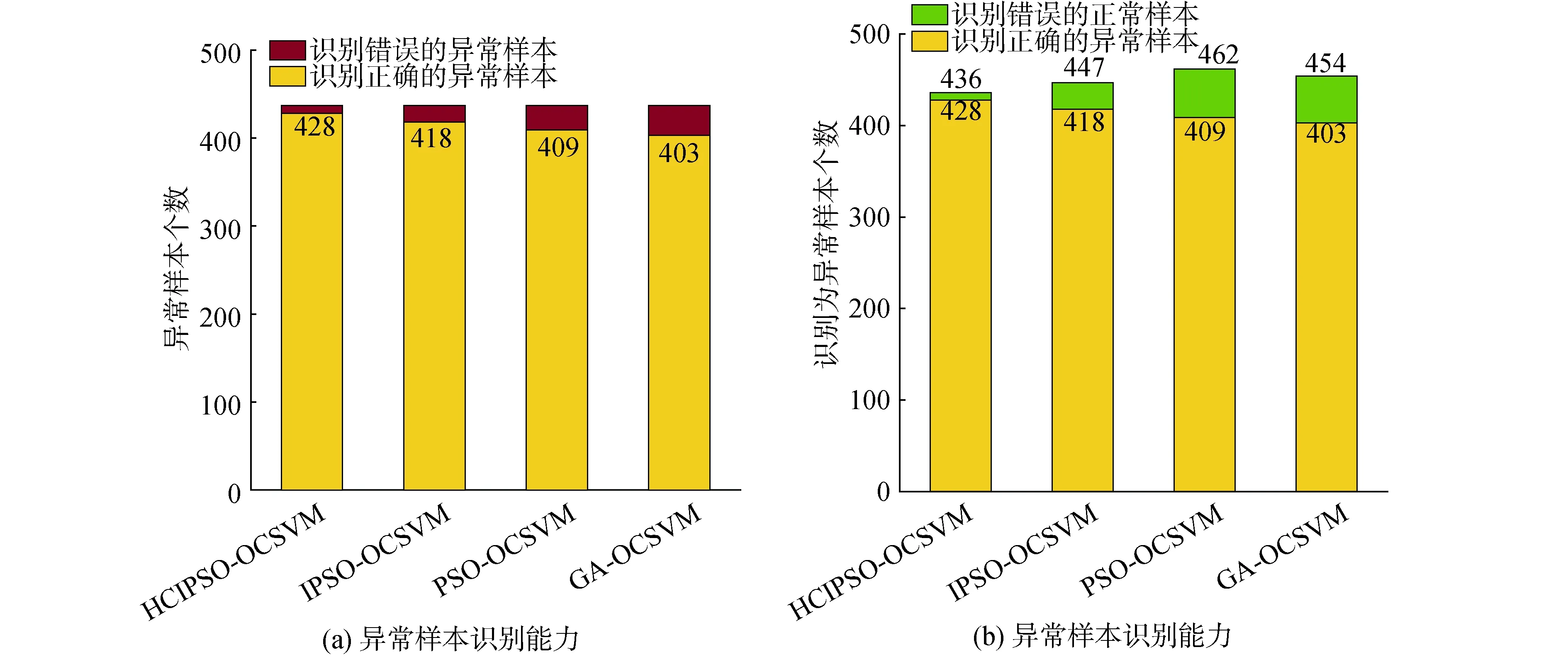
图6 异常样本的识别能力和识别精确度Fig.6 Abnormal sample recognition ability and recognition accuracy

为了进一步验证本文方法的优势，对比分析孤立森林(isolation forest,Iforest)、自编码(robust deep autoencoders,AE)、深度嵌入聚类(deep embedding clustering,DEC)[11]、鲁棒深度自编码(RDA)算法[12]对该数据集的总体检测效果，具体结果如表4所示。

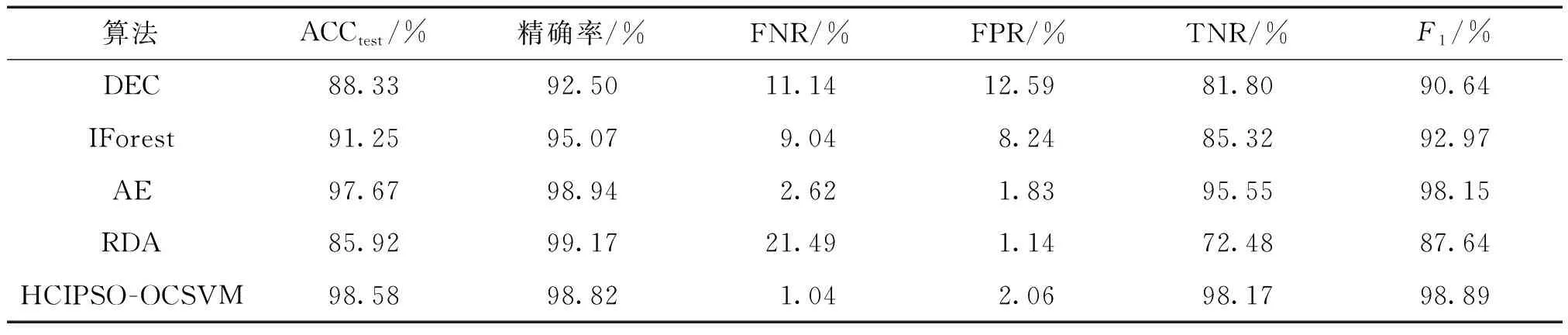
表4 不同类型入侵检测算法结果对比Table 4 Comparison of results of different types of intrusion detection algorithms

从表4可以看出，AE算法和本文方法性能接近且均优于其他方法，其FPR指标略低于本文方法，FNR指标略高于本文方法。从F1指标来看，本文方法的适用性略优一些。

通过对上述实验结果的分析可知，本文所提出的改进的OCSVM入侵检测模型的ACC和Precision指标有明显提升，同时FNR和FPR等指标也显著降低,说明该模型对正常样本数据和异常样本数据都有较高的识别能力，适用于工业控制系统的安全防护。

4 结论

1)采用FKPCA方法综合考虑样本的类别信息和总信息量对工业数据集进行特征提取，以消除数据冗余，降低数据维度，便于后续入侵检测模型的训练；

2)采用HCIPSO算法对OCSVM参数进行寻优，解决了粒子群易陷入局部收敛等问题，增强了算法的综合性能；

3)构建基于FKPCA-HCIPSO-OCSVM的入侵检测模型，并与几种参数优化算法及其他类型的入侵检测算法进行对比实验；

4)由实验结果可知，相对于其他算法，本文算法在各方面的检测性能均具有一定优势，能够较好地满足工控系统对入侵检测的需求，有一定的实用价值。