高超声速飞行器自适应固定时间抗饱和控制

刘继承， 江驹， 阴浩博， 刘亮

(南京航空航天大学 自动化学院，江苏 南京 210016)

高超声速飞行器作为一种新型快速响应和战略打击工具，其具有巨大的军事价值和潜在的经济价值[1]。我国相关航天院所开展了高超声速飞行器重大科技研发[2]。高超声速飞行器是一个集强非线性、强耦合和快时变等影响于一身的复杂被控对象，且其飞行环境易受外界复杂随机干扰的影响，因此如何设计出高效的制导控制系统是研发的关键技术之一[3]。

迄今为止，许多先进的控制方法已经应用于高超声速飞行器的控制系统的设计当中，如：滑模控制、鲁棒H∞控制、自适应控制、神经网络控制和模糊控制等。文献[2]在考虑参数不确定和外界干扰的环境下设计了一种基于干扰观测器的高超声速飞行器自适应高阶滑模控制器，能够在保证系统较强鲁棒性的同时减小抖振影响，且能保证系统的有限时间收敛特性。文献[4]基于高阶奇异值分解后的高超声速飞行器线性变参数模型设计了一种混合鲁棒H2/H∞LPV控制器，保证了对纵向速度和高度参考轨迹的渐近跟踪。文献[5]针对非线性高超声速飞行器模型中的非匹配不确定性，提出了一种自适应反步控制，并设计了投影算子以避免奇异问题，保证了闭环不确定系统指令的渐近跟踪。文献[6]设计了一种结合神经网络近似与最小学习参数(MLP)的新型改进反步法控制器，具有控制策略简洁、计算量小等特点。文献[7]采用T-S模糊建模技术对高超声速飞行器建模，针对该模型设计H∞动态输出反馈控制器，通过仿真验证了这种控制方法对参数摄动的鲁棒性。针对高超声速飞行器的固定时间控制问题，文献[8]针对高超声速飞行器严格反馈非线性系统设计了一种基于反步法固定时间控制器，并结合超螺旋结构的自适应固定时间干扰观测器，保证了系统的半全局一致固定时间收敛特性。文献[9]针对高超声速飞行器执行器故障设计了一种改进的固定时间滑模控制器，构造了快速固定时间积分滑模面，并采用了固定时间超螺旋形式趋近律。文献[10]针对不确定非线性系统提供了一种新型自适应控制策略，在该策略下，系统可以保证固定时间稳定，且不受初始状态的影响。对于抑制高超声速飞行器执行器饱和问题，文献[11]结合了基于干扰观测器的终端滑模控制器与有限时间收敛的抗饱和补偿器，实现了更好的跟踪性能与更快的响应速度。文献[12]通过引入辅助系统设计了实际有限时间自适应快速积分滑模控制器，能够处理输入饱和问题。文献[13]针对参数摄动和外界干扰下的高超声速飞行器纵向模型设计了鲁棒自适应控制器，采用反步法和非线性干扰观测器结合的方法，并为解决执行器饱和问题设计了新型辅助系统以补偿期望的控制律。

本文考虑了高超声速飞行器在具有参数不确定、外界干扰以及执行器饱和情况下的固定时间控制问题。基于积分滑模理论与自适应控制相结合的方法本文设计了2个固定时间自适应滑模控制器，使得系统状态在固定时间收敛到平衡点，并利用李雅普诺夫理论给出了严格证明，最后通过对比仿真实验验证了所提方法的有效性。本文主要创新之处如下：1)与文献[2]和文献[12]中积分滑模面的设计方法不同，本文首先给出了非线性系统的高阶滑模快速固定时间控制律的设计方法，然后基于此方法设计积分滑模面可以保证系统跟踪误差及其导数均可在固定时间内一致最终有界。2)本文设计了一种参数自适应律，表现为非线性微分方程的形式，这种设计方法能够保证不确定系统的固定时间稳定特性。3)本文设计了一种自适应固定时间抗饱和补偿器，可以保证饱和系统的稳定性且使其快速退出饱和区域。4)本文采用了精度高、鲁棒性强、收敛时间短的高阶滑模固定时间微分器，与文献[14]中的有限时间鲁棒微分器相比，能够实现更加快速地对系统状态及高阶导数的高精度逼近。

1 高超声速飞行器控制问题

1.1 高超声速飞行器模型

选取文献[22]中美国国家航空航天局兰利研究中心提出的刚体高超声速飞行器纵向模型：

(1)

式中：V为速度；γ为航迹倾斜角；q为俯仰角速率；α为攻角；h为飞行高度；μ为地球引力常数；r=h-RE，RE为地球半径；ci(i=V,γ,q,α,h)为外界时变的大气扰动；L、D、T和Myy分别为作用于飞行器的升力、阻力、推力及俯仰力矩，其表达式为：

(2)

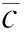
(3)

式中：δe为升降舵偏转角；Δci(i=L,D,β,Mα,Mq,Mδe)为系统建模不确定。

高超声速飞行器发动机模型采用典型二阶系统：

(4)

式中：φc为节流阀开度指令值；ωn和ξ分别为系统自然频率和阻尼比；Δcφ为外界扰动。式(1)～(4)参数的标称值可参照文献[22]。

系统控制输入u选为[φcδe]T，考虑执行器输入饱和存在，因此采用饱和函数sat(u)对控制输入进行限制，定义为：

式中：uimax和uimin为第i(i=1,2)控制输入的最大最小限幅值。定义理想控制输入与实际控制输入之间的差值为：

Δui=sat(ui)-ui

式中ui是需要设计的控制指令。

本文针对高超声速飞行器纵向模型，以控制飞行器速度和高度为目标。在模型非线性、参数不确定、外界干扰及控制输入饱和的情况下，通过设计飞行器输入节流阀开度φc以及升降舵偏转角δe实现对期望速度指令Vd和高度指令hd固定时间内的稳定跟踪。

1.2 输入输出线性化

本文采用李导数的方法对高超声速非线性模型进行线性化，根据文献[2]，对速度V和高度h分别微分3次和4次，控制输入φc和δe出现在最后的微分式中，系统相对阶为7，与系统的阶数相等。因此，闭环系统没有零动态，可以实现输入输出线性化，当考虑建模不确定性和外界扰动，反馈线性化模型可以写作：

(5)

1.3 相关引理

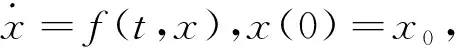
式中：α、β>0,p>1>q>0均为常数，则该系统为全局固定时间稳定，且收敛时间T1满足：

引理2[8]考虑标量系统：

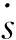
引理3[18]对于任意(x,y)∈R2，不等式成立:

式中：ε>0，p>1，q>1且满足(p-1)(q-1)=1。

引理4[20]对于xi∈Rn,i=1,2,…,n，实数p和q满足01，则下面的不等式成立：

引理5[21]考虑如下积分链系统：

(6)

式中：xi(i=1,2,…,n)为系统状态变量；u为系统控制输入。若控制器设计为：

LHsigβ1(x1)-…-LHsigβn(xn)

式中：LL、LH≥1，且多项式sn+kLnsn-1+…+kL1为Huiwitz多项式。存在ε∈(0,1)，使αn=αε∈(1-ε,1)且βn=βε∈(1,1+ε)，如果参数αi和βi满足：

式中：i=2,3,…,n，且满足αn∈(1-ε,1),βn∈(1,1+ε)，ε∈(0,1)为充分小的正数，αn+1=βn+1=1，则闭环系统式(6)是固定时间稳定的。且收敛时间的上界随LL和LH的增大而减小。

2 控制器设计

2.1 固定时间积分滑模面的设计

为了实现系统状态在固定时间内收敛，本节基于引理5分别设计速度和高度子系统的积分滑模面sV和sh为：

(7)

式中：LV1、LV2、LH1、LH2>0κi、αi、βi>0(i=1,2,3)λj、pj、qj>0,(j=1,2,3,4)，且需满足αi、pj>1,0<βi,qj<1。eV=V-Vd,eh=h-hd分别为速度和高度跟踪误差。

由式(7)可知，滑模面sV和sh的表达式中包含eV和eh及其高阶导数值，而其高阶导数无法直接测量。本文采用具有精度高、鲁棒性强、固定时间收敛的高阶滑模微分器[15]，获取eV和eh的微分估计值。为简洁，只给出eV的高阶滑模微分器为:

(8)

式中：k0、k1、k2为微分器待设计参数，其值需满足Hurwitz多项式s3+k0s2+k1s+k2；α>0为充分小的正数；θ定义为:

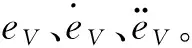
令s=[sVsh]T，考虑飞行器参数不确定及外界干扰，对滑模面变量s求导并将式(7)和式(5)代入可得：

2.2 自适应抗饱和控制器的设计

考虑控制输入受到执行器范围的限制，基于文献[24]，本文设计新型辅助系统：

(9)

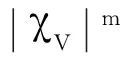
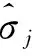
式(9)中设计的辅助系统能够保证系统在饱和状态下的固定时间收敛特性。

定义变量z=[zVzh]T=[sV-χVsh-χh]T，则

Ξ+Λ0χ+Λ1sigαχχ+Λ2sigβχχ-

(10)

式中：

根据式(10)，基于引理2设计固定时间抗饱和动态逆期望控制律为：

(11)

式中：Ki=diag(kVi,khi),(i=0,1,2)，kVi>0，khi>0，ν1>1，1>ν2>0，ϑ>0为待设计参数。

将期望控制器律式(11)代入式(10)整理可得：

(12)

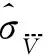
(13)

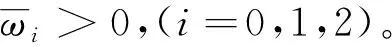
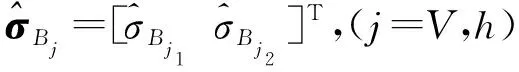
(14)

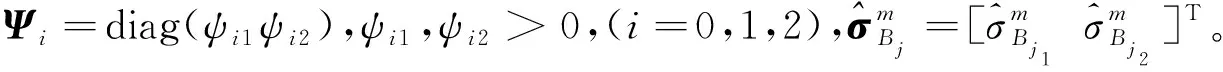
2.3 闭环系统稳定性证明

定理1对于不确定系统式(5)，无论执行机构是否饱和，选取滑模面函数式(7)、辅助系统式(9)、控制律式(11)、参数自适应律式(13)及式(14)，可以保证系统状态z是固定时间稳定的。当执行机构离开饱和区域时，系统跟踪误差eV和eh能够在固定时间内一致最终有界。

证：证明分为2部分，首先证明系统状态z的收敛，第2步分析自适应抗饱和补偿器在抑制饱和方面的作用，证明系统在非饱和状态时跟踪误差的固定时间收敛特性。

1)选择如下Lyapunov函数：

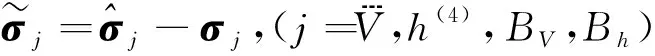
对V求导，并将式(12)代入可得：

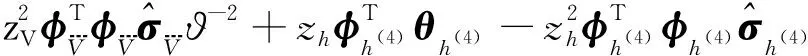
(15)

根据引理3可知：

(16)

将式(16)代入式(15)中，整理可得：

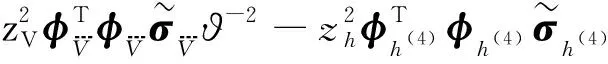
考虑自适应律式(13)及式(14)，有：

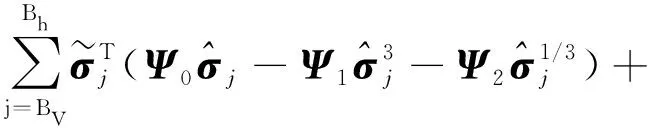
(17)

其中，根据引理3有：

(18)

且下列不等式成立：

(19)

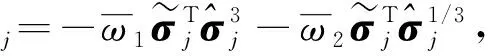
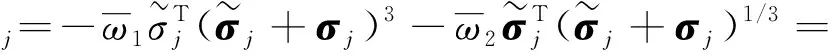
根据引理3及引理4，不等式成立：

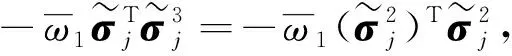
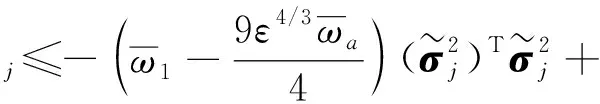
(20)

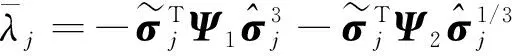
(21)

式中：ψi=min{ψi1ψi2}；ψa=ψ1+ψ2。

综合式(21)、(20)、(19)及(18)，式(17)可以重新写作：

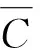
记

根据引理4可以整理得：

(22)

通过选择相应的参数使K1,min、K2,min足够大，则收敛时间与收敛区域均可任意小。

2)由步骤1)的分析可知，变量z的固定时间收敛特性不会受到执行机构饱和的影响。如果执行器不处于饱和状态，即Δuj=0,(j=1，2)，则式(9)变为：

取Lyapunov函数：

对Vχ求导有：

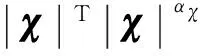
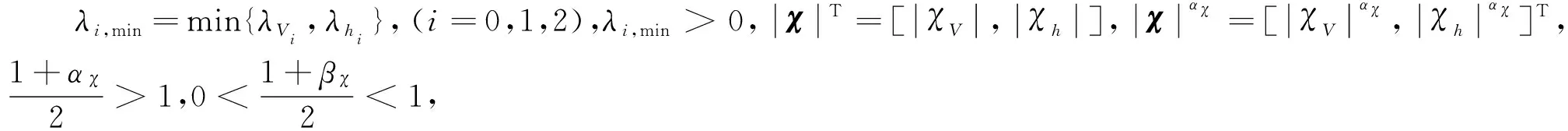
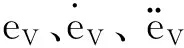
3 仿真验证

为了验证第2节设计的控制器的有效性和鲁棒性，以及闭环系统的固定时间收敛特性。本节基于Matlab/Simulink平台分别采用2种控制方法进行对比仿真实验。其中高超声速飞行器仿真初始状态为V0=4 590.3 m/s,h0=33 528 m，α0=2.7°,γ0=0°，控制器参数设定值如表1所示。

表1 控制器参数设置Table 1 Parameters of controller

模型参数不确定考虑为:

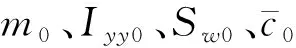
考虑实际飞行环境，速度和高度指令信号分别设置为Vd(t)=Vd0+Vd1(t)和hd(t)=hd0+hd1(t)，其中Vd0=V0+ΔV0,hd0=h0+Δh0,ΔV0和Δh0为初始跟踪误差，Vd1(t)和hd1(t)由以下滤波器产生：

式中Vstep和hstep分别为100 m/s和100 m的阶跃信号。

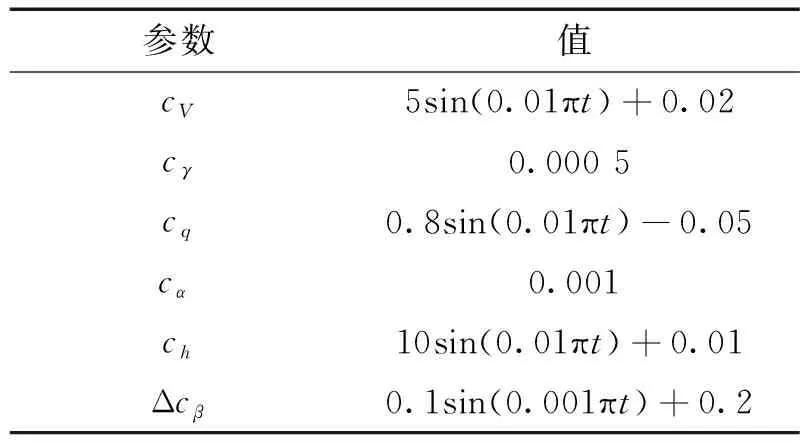
表2 外界扰动变量取值设置Table 2 Parameter values of external disturbances

仿真结果如图1～5所示，其中图1为2种不同控制方法下的高超声速飞行器速度跟踪曲线及误差变化曲线、高度跟踪曲线及误差变化曲线。其中初始跟踪误差ΔV0=2 m/s，Δh0=-2 m，假定飞行50 s后遭遇外界扰动。从图1和图2的仿真结果中可以看出，本文提出的自适应固定时间控制器相对于传统高阶滑模控制器在速度和高度子系统中都具有更好的跟踪效果，速度误差和高度误差都能实现固定时间高精度收敛，且系统收敛时间稳定在后者的47%附近。且对于暂态过程而言，自适应固定时间控制方法有更快的响应速度和更小范围内的抖振。对于引入外界干扰后的不确定非线性系统，自适应固定时间闭环控制系统表现出更好的鲁棒性和抗干扰性能。

图1 速度跟踪响应Fig.1 Velocity tracking response

图2 高度跟踪响应Fig.2 Altitude tracking response

图3(a)～(c)分别为2种不同控制方法下攻角α、航迹倾斜角γ以及俯仰角速率q的变化曲线图。相对于传统高阶滑模控制方法，本文提出的自适应固定时间控制方法能够使得各状态量在更短的时间内达到稳定值，同时也具有更为平滑的过渡状态。

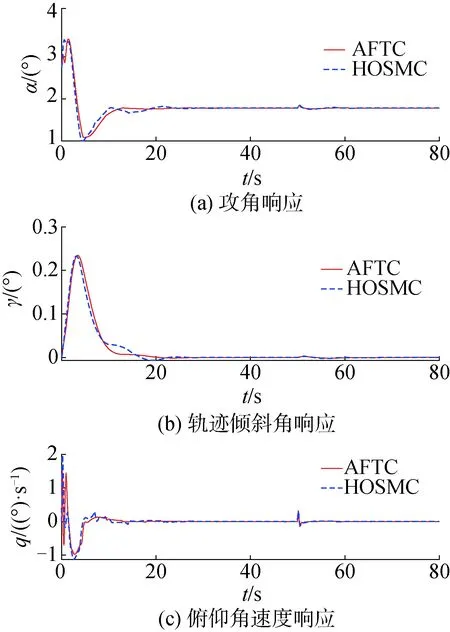
图3 攻角、航迹倾斜角及俯仰角速率响应Fig.3 Responses of attack angle, flight path angle and pitch angle rate

图4(a)～(b)为控制输入φc与δe的变化曲线，由图4中可以看出自适应固定时间控制方法下过渡过程的控制输入表现出更小范围内的抖振。且在表1的控制器参数、控制器增益参数设置条件下，该控制方法并未发生执行器饱和现象，而高阶滑模方法下的控制输入φc在初始阶段发生了饱和现象。

图5(a)～(b)分别为2种控制方法下的滑模面函数SV和Sh变化曲线图。由图5中可以看出，本文构造的滑模面式(7)以及设计的趋近律式(11)能够满足速度和高度滑模面均能在固定时间内收敛。且相对于传统高阶滑模控制方法对滑模面和趋近律的设计形式，本文的设计在仿真实验中表现出更快的收敛速度和更平滑的过渡过程。

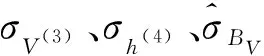
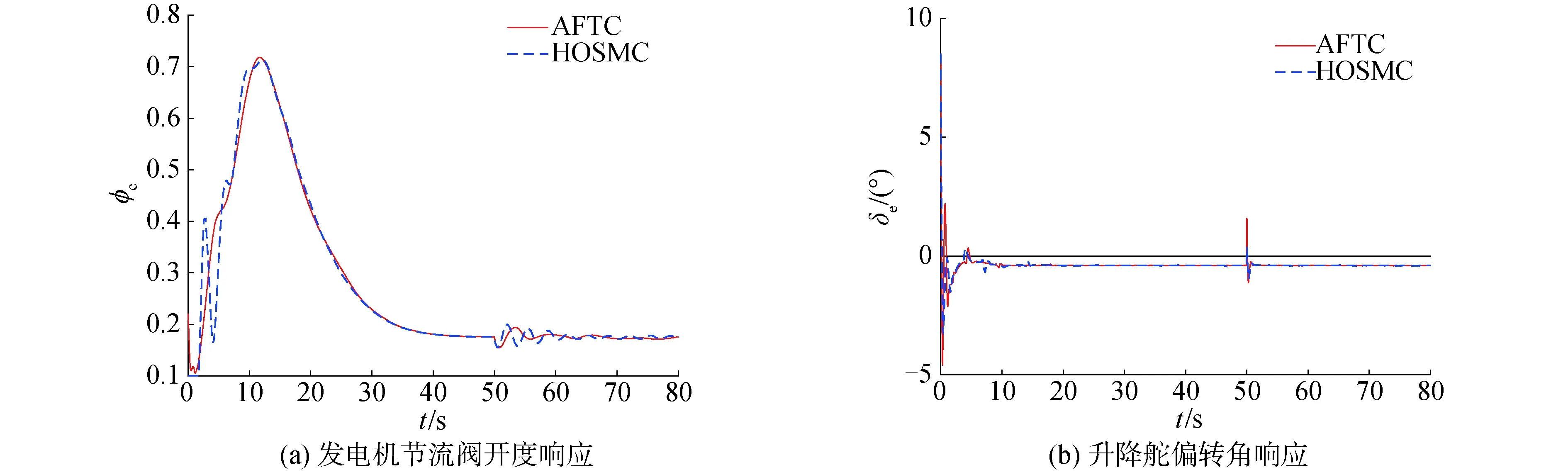
图4 控制输入响应Fig.4 Responses of control inputs

图5 滑模面SV、Sh变化曲线Fig.5 Sliding mode resonse curves of SV、 Sh

图6 自适应参数变化曲线Fig.6 Adaptive parameters response curves

4 结论

1) 对于速度和高度2个通道，论文中所设计的控制器均能够抑制飞行过程中的参数不确定和外界干扰对飞行控制系统带来的影响，表明了控制器具有较强的鲁棒性。

2) 论文引入高阶滑模固定时间收敛的概念，在有效抑制控制器抖振的同时，保证了滑模面以及系统误差的固定时间收敛特性。仿真实验表明，与传统的高阶滑模控制器HOMSC相比，本文控制方法对于高度和速度指令均具有更好的跟踪效果。

3) 论文提出的新型抗饱和辅助系统，不仅能够解决高超声速飞行器执行器物理受限下的控制问题，而且也能保证一旦离开饱和区域后，系统状态仍能在固定时间内收敛。

未来的研究工作可以按照如下的2点展开：

1) 本文只针对高超声速飞行器的纵向模型展开了研究，进行了控制器的设计。接下来的工作可对其横侧向模型及控制器设计深入研究。

2) 对本文的进一步研究，需要采取半物理仿真和实验室实验等方式来验证。