FAHP在尖山地采矿山采矿方法优选中的应用

陈树林 李 亮 薛丽娟 周科平 袁丹灵

（1.攀钢矿业有限公司攀枝花铁矿；2.中南大学资源与安全工程学院）

矿山的安全和经济都与采矿方法密不可分，因此采矿方法的选择对矿山发展至关重要。而采矿方法的选择是一项复杂而系统的工作，前期数据的匮乏和价值等指标的不确性都给采矿方法选择带来了困难。为选出最优采矿方法，学者们展开了大量研究。Li、Hezaimia 以及陈庆发等［1-3］针对不同的侧重点进行了采矿方法的选择研究。Ipha 等［4］基于软件工具开展了采矿方法比选研究。周科平、Han和Bajić等［5-8］将经典数学理论作为采矿方法决策的辅助手段。周科平、Shohda 以及Afradi 等［9-11］基于系统科学和机器算法进行了大量地下采矿方法决策研究。

以上的研究主要可以分为两大类，一是定性指标类，这类研究主要依靠工程类比和现有的经验，研究的精度不够，存在最优方案变为次优方案的风险；二是量化指标类，将获得解析解作为选择最优采矿方法的依据。但采矿过程的一些因素很难准确量化，强调对不确定性因素的量化则会导致过度量化，产生次优方案成为最优方案的危机。为兼顾不确定性因素和可量化因素对采矿方法选择的影响，将模糊数学和层析分析相结合的方法是一种可行的思路［50］。本研究将模糊层次分析（FAHP）与采矿的实际相结合，形成了适合地下金属矿山采矿方法比选的分析方法，并将其应用于攀枝花铁矿尖山地采矿山，以期避免在采矿方法决策中的欠量化和过量化的问题，提高采矿方法决策效率。

1 FAHP理论及方法

1.1 综合评价指标体系

地下金属矿山的开采是一个复杂的过程，安全高效的采矿方法是地下开采的核心，而采矿方法比选涉及因素众多，因此需建立采矿方法比选的评价体系。采矿方法主要涉及经济、技术和安全三大类指标。本研究将地下金属矿山的10个因素作为评价指标，具体见图1。基于FAHP 的原理建立了如图1所示的地下金属矿床开采方法比选的综合评价指标模型［12］。根据对采矿方法选择影响较大的10 个因素，确定其指标集为X=（X1，X2，X3，X4，X5，X6，X7，X8，X9，X10）。其中，可以获取较为准确数值的指标包括：X1、X2、X3、X4、X5、X6；X7、X8、X9、X10为不易量化的指标。

1.2 计算方法

1.2.1 判断矩阵构造

根据模糊数学理论，构造判断矩阵需如表1所示的比较标准［13］。专家根据表1 打分取值方法建立判断矩阵D1、D2、D3、D4。分值所对应的意义为i元素对于j元素的重要程度，i比j重要的取值介于中间的取值分别为2，4，6，8；j比i重要的取值介于中间的取值分别为1/2，1/4，1/6，1/8。

?

1.2.2 判断矩阵的一致性检验

分别求出D1、D2、D3、D4矩阵最大特征值λ1max、λ2max、λ3max、λ4max和特征向量ω1、ω2、ω3、ω4，通过一致性检验判断上述判断矩阵取值是否合理，如果合理就继续往下计算，如果不合理就返回第二步修改判断矩阵［14］。在计算出一致性指标的基础上，然后求一致性指标和平均随机一致性指标的比值，从而实现一致性检验［14］，即

式中，CI 为一致检验指标；CR 为一致检验指标比率；n为矩阵维数；RI为平均随机一致性指标，见表2。

?

RI 的取值来自于充分多的n阶成对比较随机判断矩阵所对应的一致性指标平均值［15］，即

如果CR＜0.1，即满足条件，获取特征向量ω。反之返回第二步。

1.2.3 隶属度矩阵

在如图1 所示的指标层中的部分指标可用确定的值量化，这类指标为定量指标。定量评判指标按其属性可细分为耗散型指标和效益型指标。将数据进行去量纲化处理，则可计算出指标层中可量化指标的隶属度［15］。

耗散型指标计算公式为

效益型指标计算公式为

式中，xkj为方案集中方案j在第k个指标下对应的特征值；rkj（r'kj）为方案集中方案j在第k个指标下的相应隶属度。

指标层中的另一部分指标难以用具体的数值进行量化，只能进行模糊评价，即定性指标。二元比较法可以对同一定性指标下不同方案的优越性比较［16］。将有限个方案进行两两比较，若Ak优于Al，则有ekl=1，elk=0；若Ak与Al的优先级别相等，则有ekl=0.5，elk=0.5；若Al优于Ak，则ekl=0，elk=1（k，l=1，2，…，m）。对ekl，elk定义，为方案的两两比较获取比较值［16］。根据以上过程得出二元比较矩阵E为［16］

当0≤eij≤1，eij+eji=1，当eij=eji，i=j时，E为优选二元对比矩阵，eij为定性指标模糊标度。

二元矩阵E按行求和并排序，比较排序最高的方案依次与其他备选方案的优选性，并得到相对隶属度，具体见表3。

注：语气位于相邻两个算子之间时，定量标度取二者均值

本研究通过上述2种方法，使不同类型的数据具有可比性，消除量纲不同给比选决策带来的影响，即隶属度一致矩阵可表示为［17］R =(ri1,ri1,…,rin),(i= 1,2,…,m)。

1.2.4 综合评判

可供选择采矿方法方案集的综合评价指标由隶属度矩阵和因素权重共同决定［13］：

式中，B为综合评判矩阵；bi为第i种采矿方法备选方案集中综合优选度，综合优选度越大的采矿方法越应当被优先选择。

2 FAHP在采矿方法比选中的应用

2.1 尖山地采矿山工程概况

攀枝花铁矿尖山地下矿山（简称尖山地采矿山）的矿床为磁铁矿矿床，以辉长岩型钒钛磁铁矿石为主。工程已控制延深最大达850 m，矿体走向近东西，倾向北，倾角50°～60°，矿体累计厚度达20～230 m，平均厚度为100.34 m。尖山矿体与围岩较稳固。

尖山地采矿山原采用无底柱分段崩落开采，为保护矿区上方交通要道，原采矿方法不能继续使用。为了协调该矿山安全与开采效益的问题，初选得到了分段凿岩阶段空场法（方案一）、分段凿岩分段空场法（方案二）、分段凿岩阶段出矿嗣后充填法（方案三）和分段凿岩分段嗣后充填法（方案四）这4种方法作为备选。

2.2 指标层权重计算

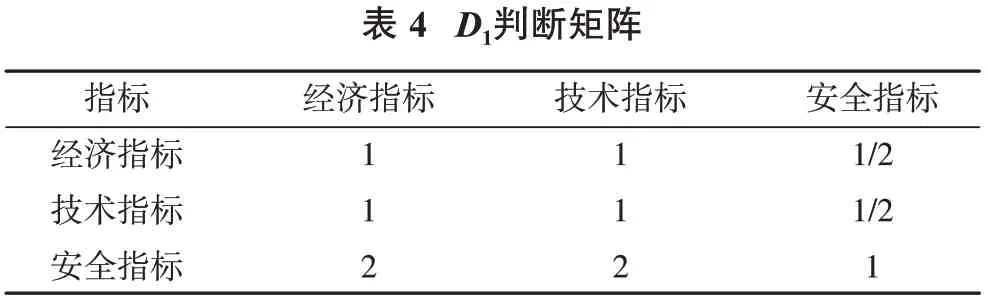
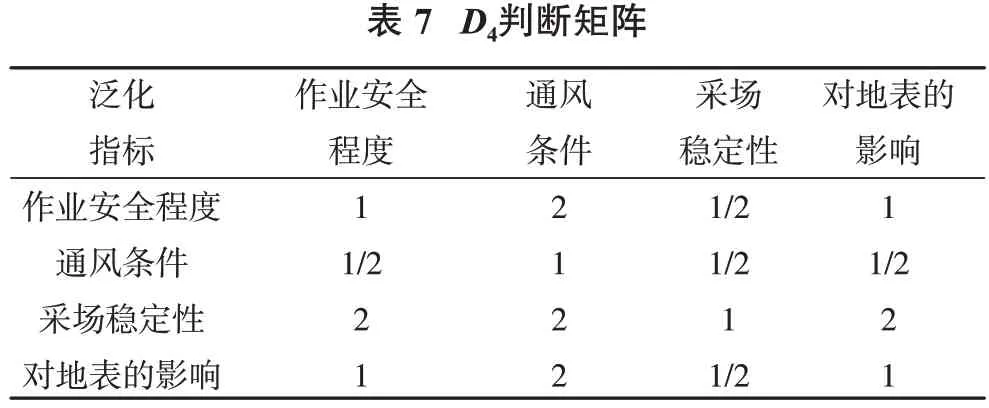
收集尖山矿地质、采矿、测量资料，开展现场工程地质调查，详细了解矿山各生产环节的运行情况，分析了矿山开采面临的关键问题，充分听取现场技术人员意见，结合专家系统决策，构造O-P-X（目标-准则-指标）矩阵。首先建立如表4 所示的准则层判断矩阵D1，然后构造出经济指标判断矩阵D2、技术指标判断矩阵D3和安全指标判断矩阵D4，具体见表5～表7。

?

?

?

?

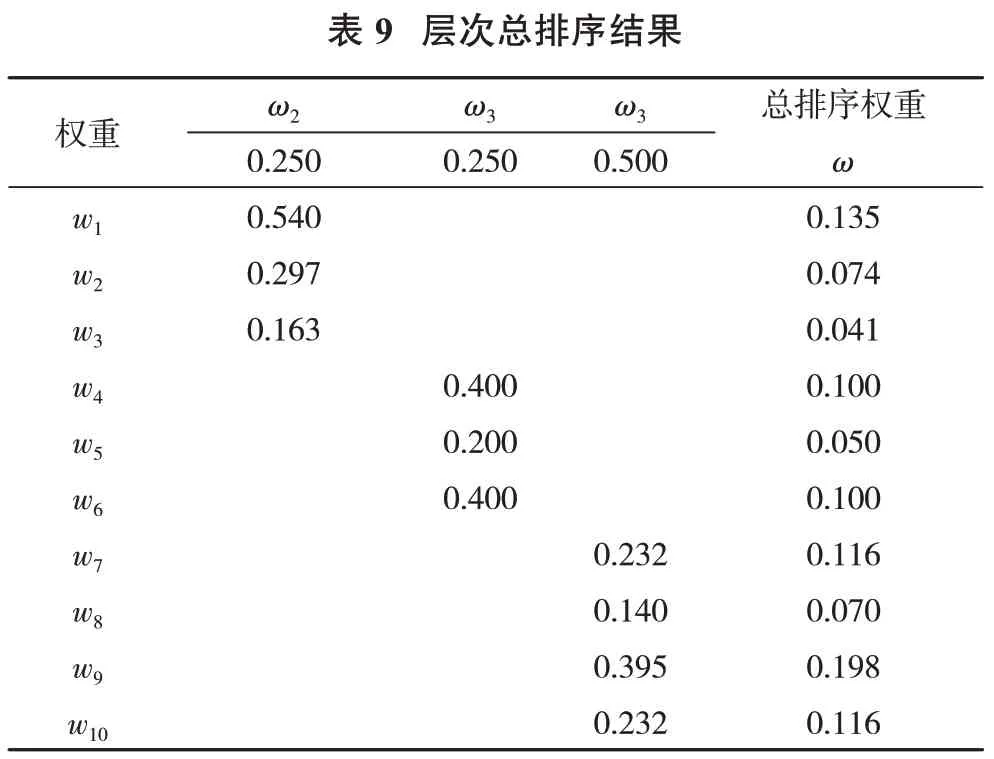
根据表4～表7 计算出各判断矩阵的最大特征值和特征向量。表8 为尖山矿4 种采矿方法的层次单排序结果。由表8可知，各判断矩阵的一致性指标比率均小于0.1，满足条件，判断矩阵取值合理。因此，将ω1中的各分量作为经济准则层、技术准则层和安全准则层的权重，ω2、ω3、ω4按照顺序合并为行矩阵，然后转置为列矩阵，矩阵中的各元素作为指标的权重。在确定准侧层和各指标的权重后，可以得到层次总排序结果（表9），并对其进行一致性检验。

?

?

在表9的基础上，经计算得出尖山地采矿山的层次总排序CR＜0.1，符合一致性要求。因此上面的层次分析的取值是合理的，能将其计算的权重作为尖山采矿方法比选评价的权重。最终得到10个指标对应的权重向量ω=（0.135，0.074，0.041，0.100，0.050，0.100，0.116，0.070，0.198，0.116）。

2.3 隶属函数

2.3.1 定量指标

根据尖山矿床的赋存状态和开采技术条件，研究中量化经济条件的3项指标（图1）和量化技术影响的3项指标，可以获得较为详实的数据，精确评分。

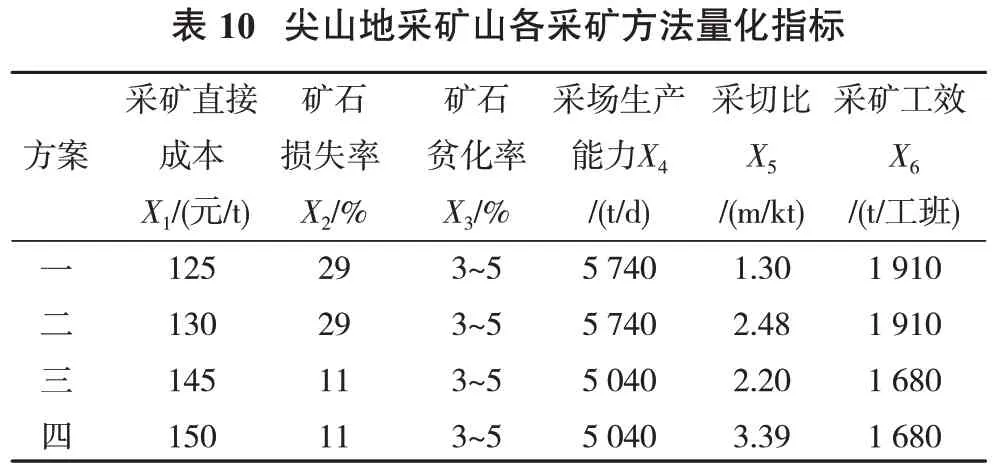
通常采用隶属度函数法计算定量指标的隶属度。尖山4 种采矿方法比选的量化指标的具体值见表10。进一步计算可以得到尖山6 个定量指标的目标矩阵，归一化处理使其量纲不同的指标具有可比性。效益型指标和耗散性指标去量纲化的方式不同，因此6 个指标各自所属类别，在尖山采矿方法的比选研究中，除采场生产能力和采矿工效，其余4 个指标为耗散性指标。经处理计算得出定量指标隶属度矩阵。

?

2.3.2 定性指标

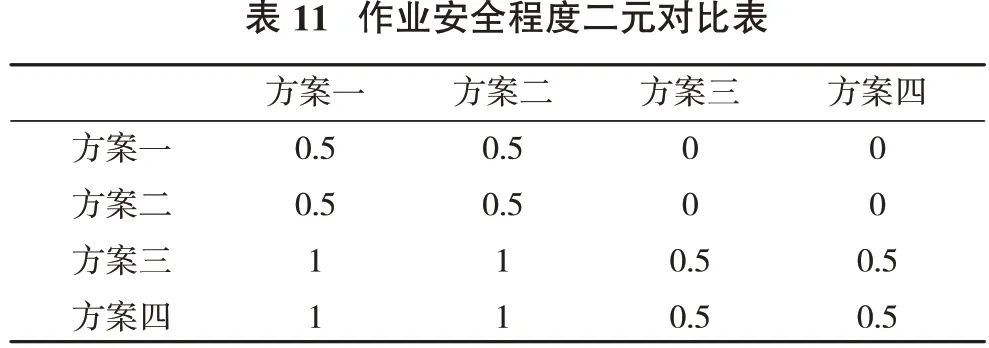
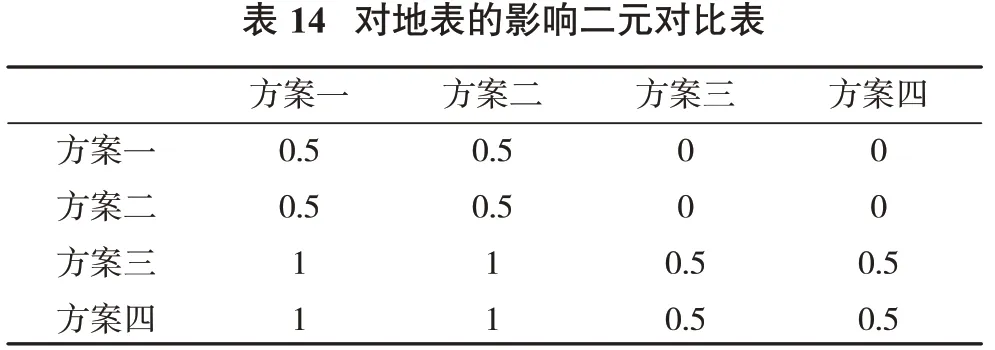
围绕尖山矿石回收中面临的安全、高效等问题，结合保安矿柱和下部矿体三维地质模型，参考FLAC3D数值模拟优化的保安矿柱范围，提出4种针对性的安全性指标，通过系统分析并以协同采矿思想为指导［18-19］，对定性采矿方案安全指标进行优选和评价。尖山采矿方法比选研究采用二元对比法确定定性指标的隶属度。通过比选得出尖山采矿方法比选的定性指标特征向量矩阵和二元对照表（表11～表14）。由于二元对照表包括了特征向量矩阵，为避免重复，特征向量矩阵不列出。

?

?

?

?

2.4 最优方案的确定

综合以上隶属度矩阵和二元对比表，得出综合隶属度矩阵为

根据已确定的权重向量和指标隶属度矩阵，最终可得尖山采矿方法评选集的FAHP 综合评判向量为B=WR= ( 0.810856 ,0.781926 ,0.93672 ,0.923005 )。

综上得出4种方法的综合优选度分别为81.09%，78.19%，93.67%和92.30%，方案集的优选次序为分段凿岩阶段嗣后充填法＞分段凿岩分段嗣后充填法＞分段凿岩阶段空场法＞分段凿岩分段空场法。因此，尖山地采矿山宜选择分段凿岩阶段出矿嗣后充填法作为其采矿方法。通过在尖山的应用研究发现，FAHP与传统方法相比，决策效率明显提高。

3 结 论

（1）发展了适合地下金属矿山采矿方法比选的FAHP，首先建立6 个定量化指标和4 个定性化指标，构造矩阵并判断矩阵的一致性，然后建立隶属度矩阵，最后进行综合评判选出最优方案。

（2）对尖山地采矿山的4种备选方法进行了模糊层次分析，得出综合评判矩阵为［0.810 856,0.781 926,0.936 72,0.923 005］，从而确定了尖山的最优采矿方法为分段凿岩阶段嗣后充填法。

（3）FAHP 同时兼顾了不确定性因素和可量化因素对采矿方法决策的影响，与传统决策方法相比，FAHP提高了采矿方法决策效率。