IMVO-SVM在短期负荷预测中的应用
李志华, 黎晓凯
(广东电网有限责任公司梅州供电局, 广东,梅州 514000)
0 引言
负荷预测是制定电力供应计划和电网电量供需平衡的关键挑战之一,它是电力市场运营的基础工作和电力规划中不可或缺的组成部分。提高短期负荷预测的准确性,有助于提高电力设备的利用率,降低能耗,缓解能源的供应端和需求端两者之间的不平衡[1]。
现阶段,围绕负荷序列的时序性和非线性特点,短期负荷预测方法层出不穷,有多元线性回归法、卡尔曼滤波法、灰色理论法、自回归积分滑动平均模型、随机森林法、神经网络法、SVM[2]。其中,SVM方法在克服高维数据、局部极值以及预测值偏差过大问题时有着极强的优势,但由于其性能好坏极其依赖参数的选取。为此,文献[3]利用遗传算法的良好全局搜索能力的特点寻优SVM参数,但其搜索速度慢且编程实现比较复杂,易陷入局部最优解;文献[4]则使用粒子群算法来选取SVM的最优参数,该方法简单易实现且需调节参数少,但同样存在局部最优解问题。
基于以上研究工作,文中提出了基于IMVO-SVM的短期负荷预测方法。针对传统MVO算法在初始种群时存在分布均匀性差的问题,不具备高效的空间搜索能力,为此对该算法进行改进并用于SVM算法的参数寻优。具体改进如下:在种群初始化过程中,引入帐篷映射的混沌序列;在位置矢量更新中,基于非线性惯性权值的下降思想,加入DE算法来搜索全局的最优解。对广东省某地市负荷数据进行预测,预测结果与GA-SVM、PSO-SVM方法所得结果对比,验证了该方法有更好的预测精度。
1 研究算法
1.1 MVO算法原理
作为一种较为新颖的元启发式优化算法,MVO算法的思想来源于多元宇宙理论[5]。定义
U=x11x21…xd1
x12x22…xd2
⋮⋮⋮
x1nx2n…xdn
(1)
式中,d为变量数目,n为宇宙数目。
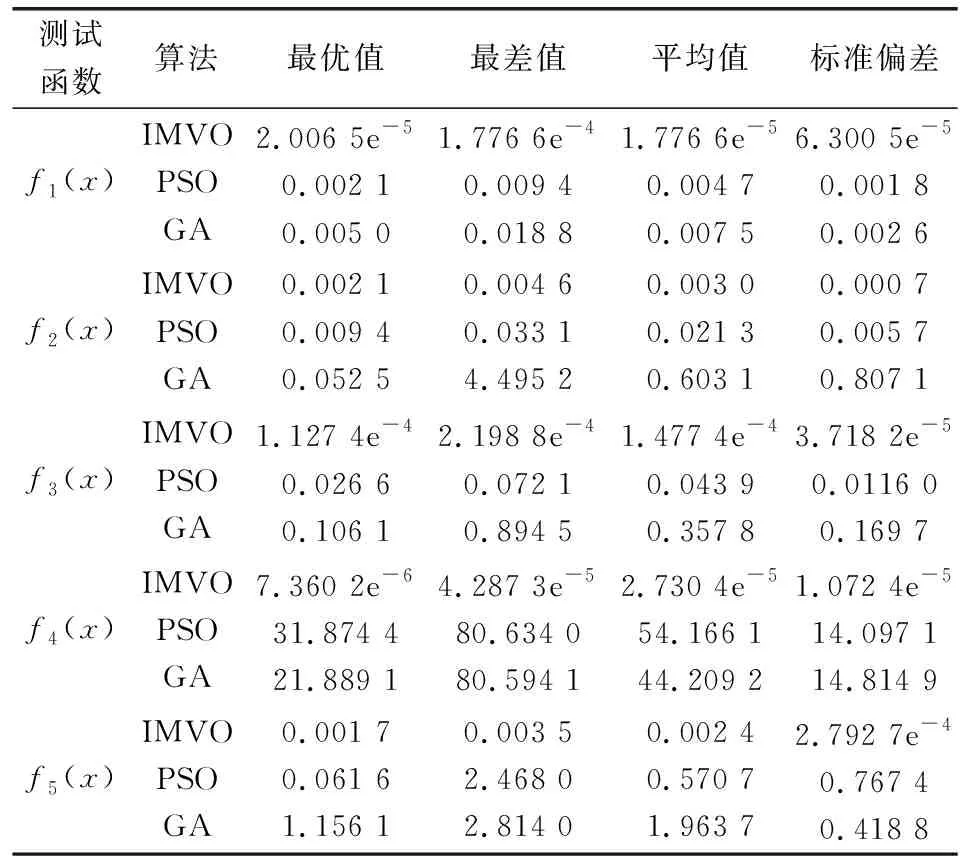
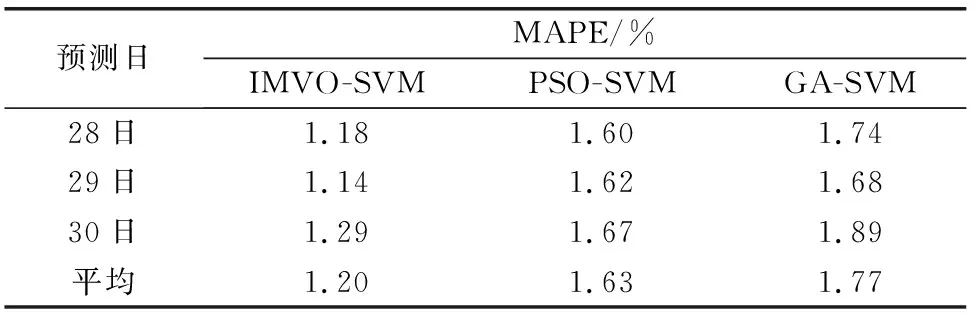
xji=xjkr1 xjir1>NI(Ui) (2) 式中,xji和xjk分别为第i个、轮盘机制所选第k个宇宙的第j个变量,r1为介于0至1间的随机数,标准化膨胀率则表示为NI(Ui)。这种机制表示为式(3): xji=Xj+TDR×((ubj-lbj)×r4+lbj)r3<0.5 Xj-TDR×((ubj-lbj)×r4+lbj)r3≥0.5r2 xjir2≥WEP (3) 式中,Xj为最优宇宙,ubj、lbj为第j个变量的上下界限,r2、r3、r4为介于0至1间的随机数,WEP为宇宙中虫洞占比,TDR为最优变换距离。表示如下: WEP=WEPmin+l×WEPmax-WEPminL (4) TDR=1-l1/pL1/p (5) 式中,WEPmax、WEPmin为WEP的上下界限,WEPmin=0.2,WEPmax=1,l为预设最大迭代次数,L为预设最大迭代次数,p的值为6,表示迭代开发的准确性。 传统MVO算法采用随机生成方法生成初始种群,粒子的分布均匀性较差,为此,本文在种群初始化过程中加入帐篷映射的混沌序列,如式(6)。 f(x)=2x0≤x≤0.5 2(1-x)0.5 (6) 帐篷映射如式(7)。 f(x)=2x0≤x≤0.5 2x-10.5 (7) 在位置矢量更新中,利用线性降权策略,以达到平衡算法在全局和局部搜索能力的目的,如式(8)。 xji=Z,r2 xji,r2≥WEP, Z=w×Xj+TDR×((ubj-lbj)×r4+lbj)r3<0.5 w×Xj-TDR×((ubj-lbj)×r4+lbj)r3≥0.5 (8) 式中,w为线性权重,表示为 w=wmin+(wmax-wmin)sinπl2L+π+1 (9) 根据正弦函数在[π,1.5π]范围内呈非线性递减的规律,w则根据迭代次数的增加进而减小。反复测试,wmax=0.7,wmin=0.2时,算法优化能力最佳。 DE算法模拟生物进化理论,用于搜索全局最优解。由变异、交叉以及选择构成。 (1) 变异,群体中的任意两个载体间,存在载体差异,通过与第三个个体求和,所产生的新变体用来进行变异操作,如式(10)。 Wi(t+1)=XR1(t)+F[XR2(t)-XR3(t)] (10) 式中,Wi(t+1)为突变所产生的新个体,R1、R2和R3为互不相等的随机数,F为0至1之间的随机比例因子。 (2) 交叉,在变异个体与新个体间互相交换一些元素,其目的是丰富个体的多样性,如式(11)。 Ui,j(t+1)=Wi,j(t+1)[0,1]≤PCR或j=jsd Xi,j(t)其他 (11) 式中,PCR为交叉概率值,sd为随机维度数目。 (3) 选择,根据适者生存的原则,有 Xi(t+1)=Ui(t+1)f[Ui(t+1)]≤f[Xi(t)] Xi(t)其他 (12) IMVO算法流程如图1所示。 图1 IMVO算法流程 SVM算法作为模式识别、回归等多个领域的重要工具,常用来解决高维、非线性以及小样本等问题的建模预测[6]。 定义:{(xi,yi)|i=1,2,…,n,xi∈Rn,yi∈Rn},其中xi和yi分别为样本的输入和输出。回归函数用于拟合(xi,yi),如下式所示。 f(x)=wTx+b (13) 式中,w为权重,b为偏移量。 将序列映射到高维空间中,利用非线性函数φ(x)构造回归估计函数,如式(14)。 f(x)=wTφ(x)+b (14) 表示优化问题: min 12w2+C∑ni=1(ξi+ξ*i) s.t.f(xi)-yi≤ε+ξi yi-f(xi)≤ε+ξ*i ξi≥0,ξ*i≥0,i=1,2,…,n (15) 式中,C为惩罚因子,ξi和ξ*i表示松弛变量,ε表示损失函数。 通过拉格朗日乘子(μi,μ*i,αi,α*i)重表达优化问题: L=12w2+C∑ni=1(ξi+ξ*i)-∑ni=1μiξi-∑ni=1μ*iξ*i+ ∑ni=1αi(f(xi)-yi-ε-ξi)+∑ni=1α*i(yi-f(xi)-ε-ξ*i) (16) 对式(16)的w求偏导,令其等于0,有 w=∑ni=1(α*i-αi)xi (17) 将式(17)带入式(13)得到函数: f(x)=∑ni=1(α*i-αi)xTix+b (18) SVM算法的回归性能的好坏,极大程度上取决于惩罚因子C以及核函数参数g的选取,为此,文中利用IMVO算法来选择SVM算法中这两个重要参数。 文中提出了一种新颖的短期负荷预测方法。首先,输入负荷数据进行归一化与划分训练集和测试集操作;其次,对IMVO、SVM的参数进行设定;接着,利用SVM建模,采用IMVO算法寻找SVM参数的最优值;最后,得到所提模型的预测结果,预测流程如图2所示。 图2 IMVO-SVM负荷预测模型过程 为了测试所提出的IMVO算法的性能,用表1所示的五个基准函数对IMVO、PSO和GA算法进行了测试。 表1 基准函数 表1中f1(x)、f2(x)和f3(x)为单峰函数,用于评估算法的优化能力;f4(x)和f5(x)为多峰函数,用于评估算法跳出局部最优解的性能。以上五个基准函数对三种算法进行10次测试,记录每个算法的测试结果。表2为各个算法的主要参数设置。测试结果见表3。 从表3中单峰函数f1(x)、f2(x)和f3(x)的测试结果可以看出GA、PSO算法的最优值、均值和标准偏差很大,IMVO算法的这三个指标则较小,验证了IMVO算法的优化能力和稳定性较好。对于多峰函数f4(x)和f5(x),IMVO算法的测试效果明显优于另外两种算法。验证了IMVO算法具有更好的跳出局部最优解的性能。 表2 参数设置 表3 测试结果 实验采用广东省某地市2017年6月16日到2017年6月30日之间的负荷数据,采样间隔15 min,共计采样点1 440个,以前面12天的数据作为训练样本,后面3天的数据作为测试样本。采用上节所提模型进行预测,图3是所提方法与GA-SVM、PSO-SVM方法的预测结果。评价指标选取平均绝对百分误差(mean absolute percentage error, MAPE),三种方法的误差统计结果如下表4。 图3 预测结果对比 表4 三种方法的误差统计 图3中可以看出PSO-SVM略优于GA-SVM方法,且在负荷峰值和谷底部分预测误差较大,而IMVO-SVM方法预测结果比较理想。在表4中,从预测日的平均值角度分析, IMVO-SVM方法的具有最好的预测精度,MAPE为1.20%,验证了该方法具有较好的预测性能。 针对SVM算法参数寻优问题,文中提出基于IMVO-SVM的短期负荷预测模型。根据传统MVO算法搜索能力缺陷,提出IMVO算法以提高其全局与局部的优化性能,并用于SVM算法重要参数的选取。以实际负荷数据进行仿真实验,与GA-SVM、PSO-SVM方法预测结果对比,验证了该方法优越的预测性能,可为短期负荷预测研究提供参考。1.2 IMVO算法原理
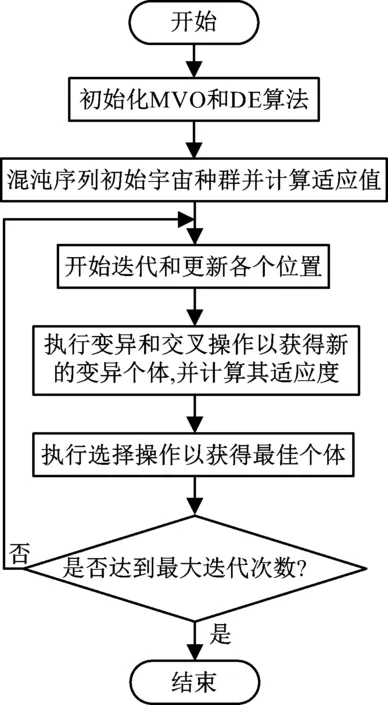
1.3 SVM算法原理
2 IMVO-SVM短期负荷预测模型
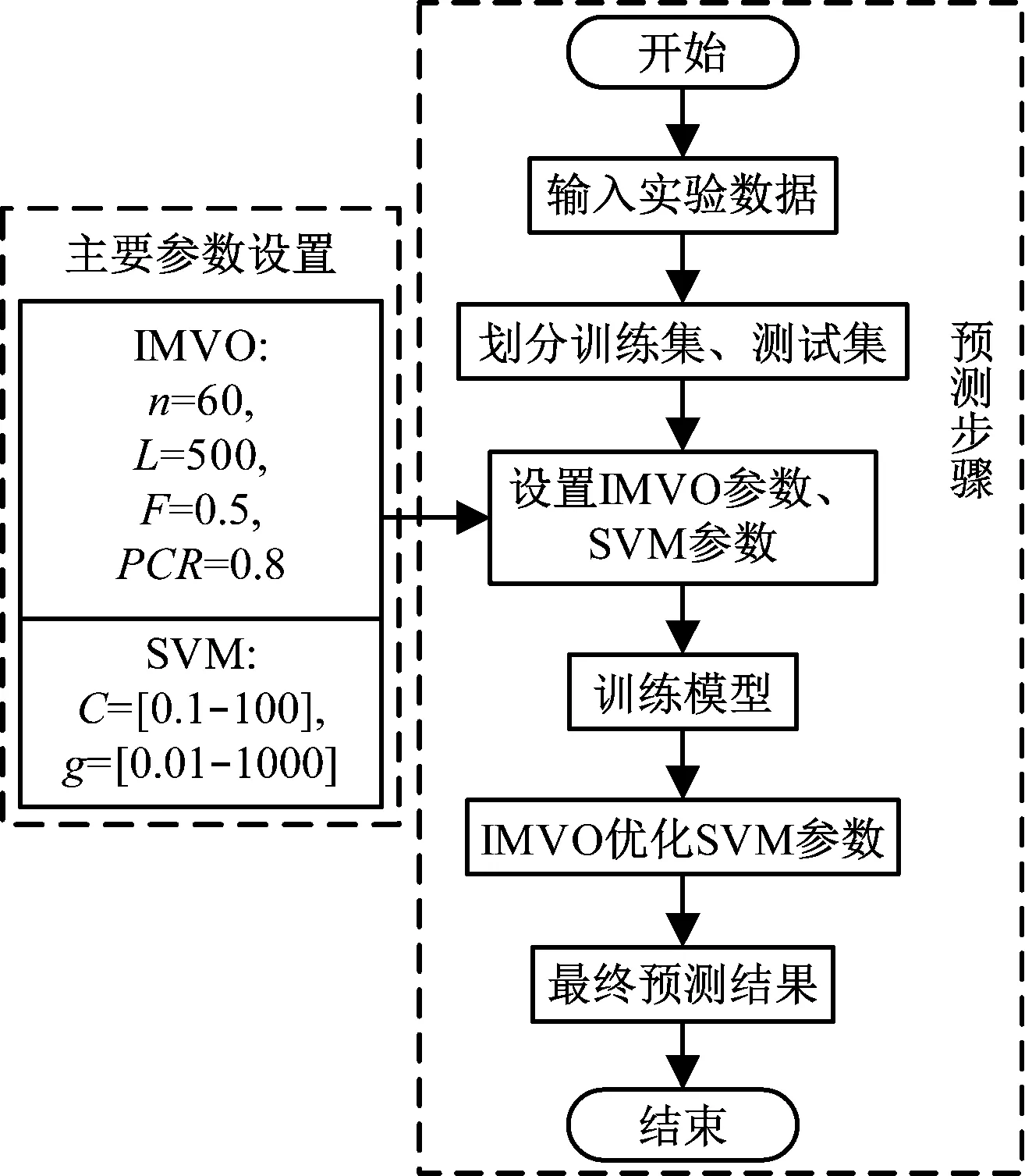
3 实验仿真
3.1 性能测试


3.2 案例分析
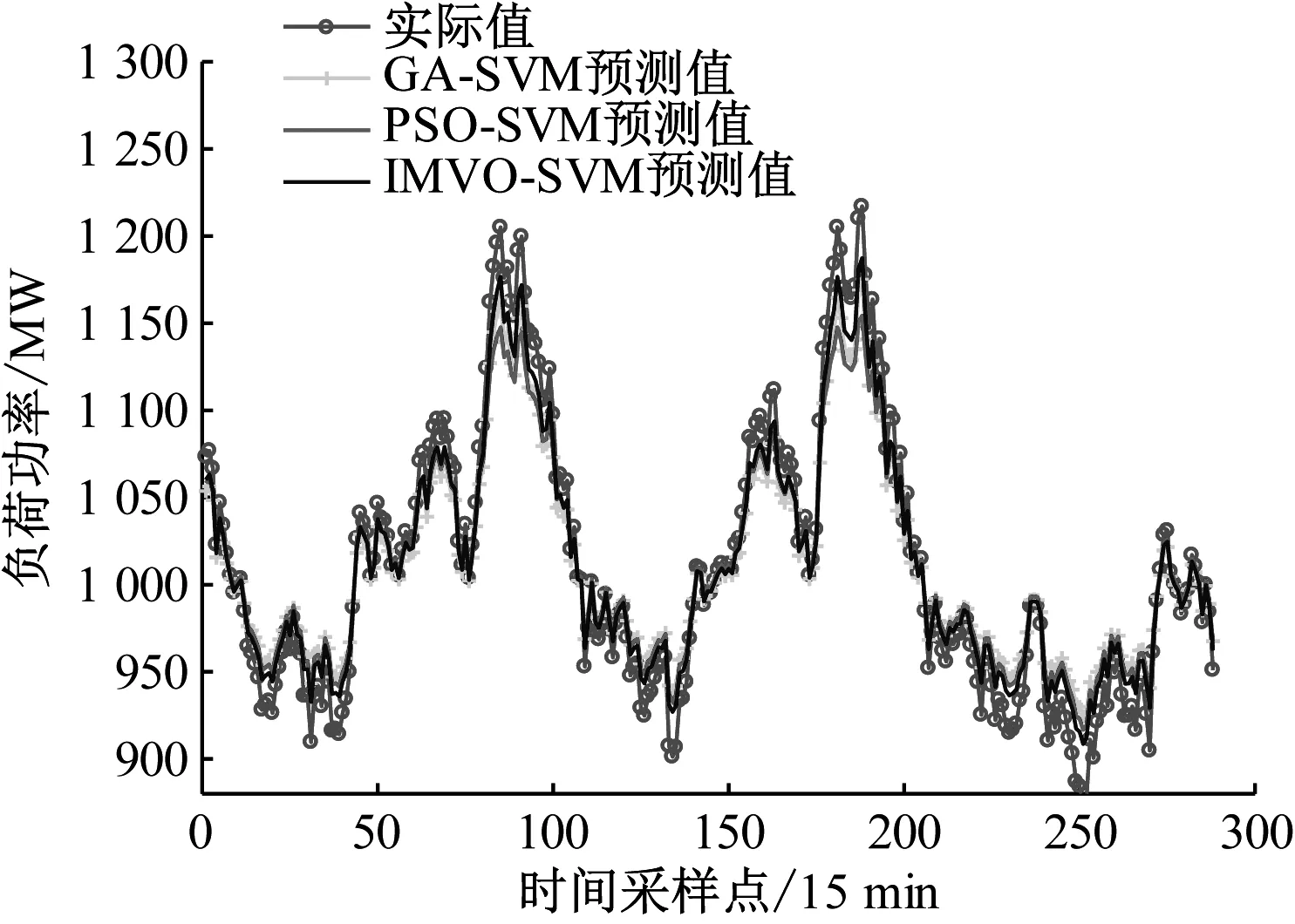
4 总结

