格栅湍流激励下的螺旋桨宽带非定常力特性

姚皞宇， 曹琳琳， 梁宁， 吴大转， 郁发新

(1.浙江大学 航空航天学院，浙江 杭州 310027； 2.浙江大学 能源工程学院，浙江 杭州 310027)

当船舶螺旋桨工作在随时间和空间变化的来流湍流中时，桨叶上的载荷变化将引起宽带非定常力，继而诱发水下推进器低频宽带噪声[1-2]。而低频宽带噪声因为其能量大、衰减慢、传播距离远等特点，一直是制约舰船声隐身性能的关键因素之一。因此，宽带非定常力作为低频宽带辐射噪声的激励源，其重要程度不言而喻。

国外学者对船舶螺旋桨宽带非定常力的研究起步较早。Sevik[3]采用了相关方法对非定常推力进行了计算，计算结果在低频段与测量结果吻合较好，但没有计算出叶频宽带峰。Thompson等[4-5]在相关法中引入与转速相关的周期项后计算出了明显的叶频宽带峰，在此基础上研究了湍流积分尺度、进速系数和桨叶间距等因素对推力谱的影响。Gavin等[6-8]系统地阐述了相关方法的计算流程，并将该方法的应用范围拓展到各向异性湍流。Wojno等[9-10]对来流格栅湍流进行了测量，发现了湍流积分尺度是流向波数的函数，从而采用谱方法计算了宽带非定常力，基于此预报的宽频噪声谱与测量结果的整体趋势吻合较好。

国内，熊紫英等[11-12]改进了谱方法中湍流径向波数谱的表达形式，并对翼型做了厚度修正，提高了谱方法的预测精度。在此基础上研究了宽带噪声与湍流特征参数之间的关系，发现来流速度和湍流度对宽带噪声总声级的贡献最大，而宽带总声压级随积分尺度增大而减小，但积分尺度对叶频宽带峰幅值的影响不是单向的。蒲汲君等[13]则采用改进的相关法研究了转速、积分尺度、桨叶数等对叶频宽带峰的影响，结果表明这些参数对宽带谱的影响机理各不相同。

然而，现有理论预报方法均是基于二维薄翼在垂直弦向阵风激励下的非定常响应函数，实际桨叶在工作中来流脉动速度既存在垂直弦向成分，也存在沿弦向成分。本文将任意阵风激励下的薄翼非定常响应函数引入相关方法，探讨了不同脉动速度诱导的脉动载荷占比情况。并从运行工况、来流特性和桨叶参数3个方面，分别研究了非定常力随转速和进速的演化规律、湍流尺度与桨叶数的匹配关系以及侧斜纵倾分布对宽带非定常力的控制效果。所得结论可为水下推进器的减震降噪设计提供参考。

1 螺旋桨非定常力的相关方法

1.1 二维薄翼升力响应

在来流湍流激励下，翼型同时受垂向脉动和弦向脉动影响。图1给出了任意方向的脉动来流中二维翼型非定常升力分解模型，其中ξ1和ξ2分别代表弦向和垂向，来流平均速度为U∞，脉动速度为u(t)。

图1 任意方向脉动激励下的薄翼非定常升力分解Fig.1 Unsteady lift force decomposition of thin wing under fluctuating excitation in any direction

将桨叶简化为无厚度的薄翼，由非定常薄翼理论可知，水翼的非定常升力由3个部分组成：

1)垂直阵风u2(t)在零攻角下的薄翼上诱导的脉动升力[14]。

式中：L0为准稳态升力；ρ为介质密度；c为弦长；u2(ω)为垂向脉动速度u2(t)的傅里叶变换；ω为角频率；k=ωc/2U∞为无因次频率;Sears函数S(k)中的Jn和Kn分别为n阶第1类和修正的第2类Bessel函数，i为虚数单位。

2)弦向阵风u1(t)作用下带攻角薄翼的脉动升力。假设攻角αc较小，则弦向阵风的来流速度近似等于U∞，并且升力方向仍垂直于翼型弦向，该部分脉动升力为：

ΔL1=πρcU∞u1(ω)αcT(k)

T(k)=X(k)+iY(k)为Horlock函数[15]：

(1)

3)弦向脉动速度激励下带拱度的薄翼的脉动升力。ymax为翼型中弧线的最大拱度，该部分脉动升力为:

式中：T′(k)为Holmes函数[16];系数a和b与式(1)中相同。因此，二维翼型的总脉动升力可视为以上三者之和。

1.2 条带法及桨叶非定常力谱

首先基于条带法[17]思想将桨叶沿径向分成若干个条带，忽略径向的流动，各桨叶条带可视为1.1节的二维翼型，如图2所示。图2(a)中全局静止坐标系原点位于桨叶参考线与轴线交点，U∞为平均来流速度，并叠加沿流向的脉动速度u，Ω为旋转角速度。图2(b)为桨叶条带上的局部坐标系，其中ξ1和ξ2方向与图1中定义一致，ξ3为沿桨叶的母线方向。忽略自由涡系在叶面上的诱导速度，则对于半径r处的桨叶条带，相对来流速度为：

第b片桨叶上，半径r处的α条带对来流单位弦向和垂向脉动速度的响应函数分别为：

(2)

式中：下标N表示垂向方向;c表示弦向方向。忽略交叉项，则α条带与位于第b′片桨叶上，半径r′处的β条带之间的脉动升力互相关谱表示为:

(3)

(4)

图2 转子条带与坐标系定义Fig.2 Definition of rotor strip and coordinate system

将式(3)、(4)代入式(2)，并求和后提取沿轴向分量即为整个螺旋桨所受脉动推力总功率谱：

(5)

图3为柱坐标系下任意2条带相对位置以及升力速度分解示意图，其中θ为周向方向，x方向与图2(a)中相同，θskew为侧斜角度，Xskew和Xrake分别为侧斜和纵倾引起的轴向位移，φ(r)为半径r处的相对液流角，其与螺距角之差为桨叶攻角，则轴向脉动速度可分解为垂向速度uN和弦向脉动速度uC。

在柱坐标中周向和径向单位向量可表示为:

er=eycosθ+ezsinθ,eθ=ezcosθ-eysinθ

(6)

图3 柱坐标下的桨叶条带与升力速度分解Fig.3 Decomposition of blade strip and lift velocity in cylindrical coordinates

桨叶局部坐标系下ξ1、ξ2和ξ33个方向的单位向量可表示为:

(7)

式中：采用了中心差分格式表示桨叶沿参考线的单位向量e3；X+、r+、θ+和X-、r-、θ-分别为相邻桨叶条带在柱坐标系中的位置参数，S为2条带间距：

且ηNx、ηNr和ηNθ分别为向量e2在柱坐标中的方向余弦。将式(6)代入式(7)可得到向量e1和e2在全局坐标系中的方向余弦ηNi和ηCi，则式(5)中弦向和垂向脉动速度相关函数为:

式中Rij(τ)为直角坐标系中湍流脉动速度相关张量，指标i、j可取x、y和z，且遵循求和约定。

1.3 脉动速度的相关函数

依据各向同性湍流理论，脉动速度的二阶相关张量可用纵向和横向相关函数f(ζ)和g(ζ)表示[18]：

鼓励教学 首先，目前专业实验教学项目类型较为单一，难度比基础实验项目稍大，本科生普遍是在开展实验初期有较高的学习积极性，随着实验教学项目的开展，兴趣逐渐被消耗殆尽。通过提高专业实验室开放性，可增加实验类型及授课方式，进而提高学生的积极性[8]。其次，本科生毕业后无论是继续深造读研还是就业创业，都需要有一定的创新能力。提高专业实验室的开放性，有助于让学生从被动学习转化为主动学习，多思考以提升创新能力。最后，对于授课教师而言，开放型的实验室有利于开展多类型的教学模式，进而增强教学效果。

(8)

式中：ζi为2点距离ζ在i方向的分量，有ζ2=ζiζi；δij为克罗内克函数。由流动连续性方程可知：

则二阶速度相关张量可用相关函数f(ζ)表示。实验研究[19]表明充分发展的格栅湍流中，f(ζ)可近似表示为e-∣ζ ∣/Λ，其中Λ为流向积分尺度，则式(8)为:

对于旋转的桨叶，作用在任意两条带上的湍流脉动间距ζ不仅与两者的相对位置有关，同时还是时间间隔τ的函数，其各方向分量分别为:

(9)

2 计算与验证

2.1 计算模型

本文以Sevik实验[3]中的螺旋桨为基础模型，桨叶叶梢半径为10.16 cm，桨毂半径为2.25 cm，桨叶各半径处等弦长，无纵倾与侧斜，设计进速系数J为1.17，三维模型如图4所示。

图4 螺旋桨模型示意Fig.4 Schematic diagram of propeller model

实验中分别采用间隔为10.16 cm和15.12 cm的格栅在距桨盘面上游20倍间隔处生成不同尺度的来流湍流。由于来流在桨盘面位置处仍会存在残留的各向异性成分，且桨叶迎风面负压引起的抽吸作用会使上游附近湍流涡产生沿流向的扭曲[20]，因此式(9)中需引入拉伸系数[6,21-22]，本文中取各方向拉伸系数ax、ay、az分别为0.8、1.5和1.5。

2.2 脉动推力成分分析

对比J=1.0、1.15和1.3下脉动推力宽频谱，并将脉动推力分解为1.1节中的3个部分。转速固定为18.43 r/s，各工况下叶梢条带的攻角分别为4°、1.6°和-0.8°，满足小攻角假设，来流湍流强度u′/U∞取3%，湍流积分尺度Λ取4 cm，计算结果如图5所示。

从图5可以看出，垂向脉动诱导的非定常推力在前两阶叶频处存在宽带峰，并且中心频率相对各叶频均存在不同程度的“右移”，这与Jiang等[5]的计算结果一致。弦向脉动诱导的脉动推力宽带谱整体则由低频向高频单调衰减，攻角诱导的脉动推力宽带峰中心频率略低于一阶叶频。而随着进速系数的降低，垂向脉动速度诱导的脉动载荷中叶频宽带峰的显著程度增加，但其他频段的量级则不同程度地下降，其主要原因是来流速度变化引起湍流宽带谱的改变。而弦向脉动速度诱导的脉动载荷在全频段均有上升，这主要是由于式(3)中攻角的增大引起。该模型各半径位置桨叶剖面拱度相对较小，因此拱度对叶频段脉动载荷的影响可忽略不计。

图5 垂向与弦向脉动诱导的非定常推力宽带谱对比Fig.5 Comparison of broadband spectrum of unsteady thrust induced by chordal and vertical fluctuation

表1 脉动推力主宽带峰幅值与中心频率Table 1 Amplitudes and center frequencies of main broadband hump

2.3 结果验证

采用文献[5]测试结果验证相关方法，2种格栅的实验工况参数分别为U∞=4.68 m/s，n=18.88 r/s和U∞= 4.6 m/s，n=18.55 r/s，进速系数均为1.22，桨盘面处湍流强度均为3.5%，流向积分尺度经测算分别为Λ=2.8 cm和Λ=4.24 cm，计算结果与实验测试的脉动推力宽带谱对比结果如图6所示。

由于考虑了来流湍流的各向异性度，因此本文计算结果中一阶叶频宽带峰与实测结果吻合度相比文献[5]更高，但谱峰幅值仍略小于实验值，这主要是因为在实验中该模型桨存在位于231 Hz附近的扭振模态[4]，在叶频脉动载荷激励下产生共振使得传递到轴上的脉动力量级增加。而在15.12 cm格栅中出现了明显的二、三阶叶频附近宽带峰，其可能原因是在实验水洞中15.12 cm格栅下游湍流脉动在横向与纵向上分布不均，引起了高阶叶频宽带的增加。总体而言，相关方法预报的结果是可靠的。

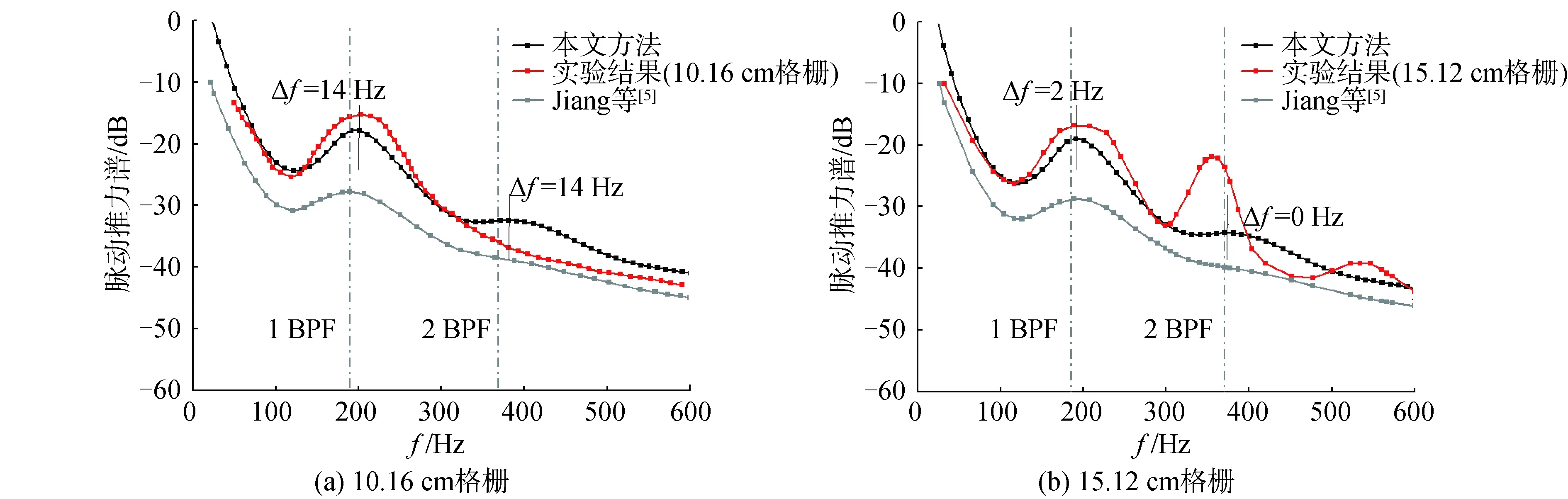
图6 脉动推力宽带谱验证Fig.6 Validation of unsteady thrust spectrum

3 宽带非定常力特性

3.1 相似工况下的非定常力演化

船舶推进器多工作于设计工况，因此选取进速系数J=1.22，来流湍流参数均与15.12 cm格栅工况下相同，脉动推力谱随转速的变化如图7所示。

图7的结果表明，来流速度增加导致了脉动绝对量级的增加，因此低频宽带成分以及叶频宽带峰量级增大，同时由于转速的增加，宽带峰中心频率提高。对图7中叶频宽带峰进行拟合发现，当转速较大时，相似工况下叶频宽带峰的幅值与转速的二次方近似成线性关系。转速和流速的同步提高，使得叶频宽带峰的带宽增加，并且宽带谱峰和低频段脉动的衰减速率减小，这与雷诺数的改变引起的来流湍流谱的差异有关。

图7 相似工况下的脉动推力宽带谱 (J=1.22)Fig.7 Broadband spectrum of unsteady thrust under similar operating conditions (J=1.22)

3.2 湍流尺度与桨叶数的匹配

2.3节对比表明，不同尺度的湍流来流下非定常力宽带峰幅值和形态随着湍流尺度的变化略有差别。图8为改变原型桨叶数后，脉动推力宽带谱随来流湍流尺度变化的结果。随着积分尺度增大，低频段的整体量级提高，但宽带谱峰谷值及二阶叶频附近的宽带峰均下降，这主要是因为采用了指数衰减函数模化来流湍流谱，造成了湍流谱中大尺度脉动量级增强，小尺度脉动强度降低，在桨叶的脉动响应中也呈现类似规律。

图8 脉动推力宽带谱随积分尺度的变化Fig.8 Variation of broadband spectrum of unsteady thrust with integral scale

另外，图8中一阶叶频处的宽带响应分别在不同的临界积分尺度下达到最大值，当积分尺度小于临界值时，一阶叶频幅值下降明显，而当积分尺度增大时幅值的降低幅度则较小，这与谱方法计算的趋势一致[11-12]。临界积分尺度分别为10、4和2 cm，与桨叶数呈反比，且与0.7R处的桨叶间距相当，由于该模型0.7R处条带上的脉动力量级最大[11]，因此，可以断定当来流中含能涡尺度与最大脉动载荷位置桨叶间距相近时，桨叶间的脉动载荷相关度最强，导致叶频处宽带峰出现极值。为降低叶频宽带脉动载荷的量级，来流涡尺度需避免与桨叶上脉动载荷极值处的桨叶间距相当，将来流湍流的积分尺度控制在临界积分尺度以下对于螺旋桨整体宽带响应的控制将更有利。

3.3 纵倾与侧斜的影响

侧斜和纵倾是降低螺旋桨线谱非定常力的有效手段，这里研究其对宽带非定常力的控制效果，仍然选取15.12 cm格栅下游湍流为输入，分别研究具有不同纵倾和侧斜分布的螺旋桨模型响应差异。桨叶的侧斜与纵倾角分布如图9和图10所示。

图9 侧斜角分布Fig.9 The distribution of rake angle

图10 纵倾角分布Fig.10 The distribution of skew angle

侧斜角θ与纵倾角γ分别为线性和四次多项式分布，其中多项式分布中各阶次系数通过对E1619桨的侧斜分布拟合得到，并依据最大侧斜和纵倾角度进行相应缩放。对于线性分布来说，最大侧斜与纵倾角为叶梢与轮毂处角度之差，而多项式分布则为叶梢处角度与0.4R处角度之差。

不同纵倾分布的脉动推力宽带谱如图11所示。

图11 纵倾对脉动推力宽带谱的影响Fig.11 Influence of rake on the broadband spectrum of unsteady thrust

总体而言，纵倾对宽带非定常推力的影响较小，且采用线性和多项式分布下的差异不大，随着最大纵倾角度的改变，一阶叶频的宽带峰幅值和低频部分基本无变化，而在多项式分布下二阶叶频的宽带峰有较小的降低。但一阶叶频左边带的峰谷却随着纵倾角的增大而上升，因此可以断定，纵倾无法有效降低宽带非定常力。

不同侧斜分布下脉动推力宽带谱如图12所示，侧斜对低频段宽带谱的影响较小，这主要因为低频段上桨叶的升力响应由来流湍流谱的特性决定，侧斜的改变无法根本性地改变来流湍流的强度及特征尺度。但一阶叶频及二阶叶频等宽带谱量级则随着最大侧斜角的增大而减小，并且，采用多项式分布对宽带谱的控制效果要好于线性分布，其中当最大侧斜角达到20°时已有较好的控制脉动推力的效果，侧斜进一步增大到40°时一阶宽带峰幅值相比原型降低5 dB，这与线性分布下60°侧斜角时效果相近，产生这一差异的主要原因与脉动升力沿桨叶径向的分布有关。考虑到侧斜的增大往往会带来附加的弯矩，对桨叶的强度产生不利影响，因此兼顾强度与减振，在本文研究的湍流来流下的最大侧斜角可控制在40°。

图12 侧斜对脉动推力宽带谱的影响Fig.12 Influence of skew on the broadband spectrum of unsteady thrust

4 结论

1)在小攻角状态下，脉动推力中由垂向脉动速度引起的宽带成分在量级上占主导，但随着攻角增加，弦向脉动速度引起的脉动推力量级提高。在设计工况附近，螺旋桨脉动推力宽带谱的计算时可以忽略弦向脉动速度，并且计算结果与实测值在一阶叶频及低频部分吻合较好。

2)随着转速和流速的同步提高，相似工况下脉动推力整体量级和叶频宽带峰量级均有提高，且叶频宽带峰的幅值与转速的二次方近似成线性关系。

3)积分尺度的增大会使宽带响应中低频段的整体量级提高，高频段量级减小。叶频宽带峰则在临界积分尺度下出现极大值。不同桨叶模型的计算结果表明，在叶型不变的情况下，临界积分尺度与桨叶数呈反比。

4)纵倾无法降低格栅湍流来流中非定常推力的量级，侧斜则可以有效地降低宽带力的叶频相关成分，且随着最大侧斜角的增大，叶频宽带峰量级降低程度越大，对于本文所研究模型桨，采用多项式形式的侧斜分布较线性分布更有利于抑制宽带非定常力。