“指向数学建模素养的可视化学习”的课堂实践

江苏省无锡市堰桥高级中学 郭桂霞

椭圆标准方程是人教版选修性必修第一册内容，分为两个课时，“椭圆标准方程”第一课时是学生学习了直线方程、圆的方程之后的后继知识，学生已具有一定的观察、分析和解决一些相关问题的能力。而推导椭圆的标准方程的方法对双曲线、抛物线方程的推导具有直接的类比作用，为学习双曲线、抛物线内容提供了理论基础和基本模式，是一个重要的数学建模示范。本文从知识导入、知识建构、知识运用三方面教学实录与评析谈谈如何在教学中通过设置适当的问题启发、引导学生思考，提升学生思维，主动建构模型，提升数学素养。

一、知识导入

情境1：播放“嫦娥五号”探测器发射升空的视频，当屏幕上出现探测器运行的轨迹时，学生齐声呼唤轨道是椭圆。

（评析：背景材料紧跟时代步伐，迅速抓住学生的注意力，能让学生触景生情，激发探索热情，认识到建模的必要性，让学生感受数学从生活中来，数学服务于生活。）

情境2：几何画板展示圆被压扁的过程

生众：椭圆。

师：以上图形从感性上看都给我们椭圆的印象，从数学理性的角度上看，它们是严格意义上的椭圆吗？为了进一步研究椭圆，我们将利用解析几何的思想，用代数的方法来研究几何问题，所以我们要研究椭圆的方程，这就是我们要研究的课题：椭圆的标准方程。

（评析：设置情境,引入疑惑,激发学生对问题的思考与反思，给出研究课题的必要性。让学生能从数学的眼光思考问题，培养思维的严密性。）

二、知识建构

师：如何求椭圆方程？关于椭圆你有哪些了解？

生众：椭圆定义。

（评析：让学生能主动地根据先前认知结构，有选择性地知觉外在信息，让思维有增长的起点。）

师：椭圆的定义是什么？

生1：平面内到两定点FF的距离的和等于常数的点的轨迹叫做椭圆。

师：常数有要求吗？

生2：常数2a必须大于FF。

师：为什么？

生3：如果常数等于FF，轨迹为线段FF；若常数小于FF，轨迹不存在。

（评析：让学生了解知识的内涵与外延，这是思维增长的必经过程。）

师：我们不会求椭圆的标准方程，回顾一下如何求出圆的标准方程。

生4：建立坐标系、设点、找等量关系、代入坐标、化简。

（评析：通过复习旧知识，并采用同化法，唤起学生对数学思想方法的提取，从而找到了知识的“生长点”。）

师：求椭圆标准方程，如何建立适当的坐标系？

生5：以FF所在直线为x轴，以过F与FF垂直的直线为y轴。

生6：以FF所在直线为x轴，以FF中垂线为y轴。

师：有两种建系的方法，大家觉哪个更好呢？为什么？

生7：第二个，图形更对称，感觉后面的运算可能更简单一点。

（评析：尊重学生思路，发挥学生主体性，并让学生学会思考思路的合理性与思路的优化、能优化的原因，培养学生思维的不断深入。）

（1）建立适当的坐标系：以直线FF为x轴，线段FF的垂直平分线为y轴，建立如图所示的坐标系。

（2）设点P(x,y)：设是椭圆上的任意一点,FF=2c，F(-c,0),(c,0)。

师：如何化简这个方程呢？大家可讨论讨论。

生8：直接两边平方；

生9：移项后两边平方；师：我们选哪种方法？生10：第二种，一边一根式，对称一些。

（评析：前面建系的对称性已在学生思维里有了意识，主动去优化方法，思维有所增长。）

在黑板上用方案2加以推导。在化简得出方程(a-c)x+ay=a(a-c)后师：能否把式子写得更简洁些？

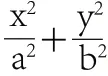
师：大家观察式子的特征，若x，y是一次的话，是什么曲线的方程？

生11：直线的截距式方程。

生12：与x轴的交点为(-a,0)，(a,0)，与y轴的交点为(-b,0)，(b,0)。

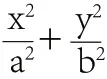
师：一次是直线，二次是曲线表示椭圆，数学很奇妙。

（评析：渗透了自然美、对称美、简洁美，帮助学生记忆椭圆标准方程。）

师：这里a，b，c的等量关系和大小关系如何？

师：那么方程是否会具有对称性呢？

生13：好像有，x，-x分子是平方，的平方一样，y，-y的平方一样。

它表示焦点在x轴上的椭圆，a是最大的（既然b=a-c，那么我们是否能在图中找到以a,b,c为边的直角三角形呢？结合图形发现△OFB）

（评析:让学生从数的角度感受到对称性，体会形与数的统一。）

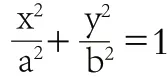
生众：圆。

（评析：从代数的角度观察椭圆与圆的区别，对情境2的直观感知的严谨化。）

师：椭圆可圆可扁，焦点在轴上的椭圆该如何表示？

（评析：类比焦点在轴上的椭圆，让学生利用已有知识,在做中学,类比学,并把新知识同化到原有知识。）

三、知识运用

例1：判断下列椭圆的焦点在哪个轴上，并写出焦点坐标：（过程略）

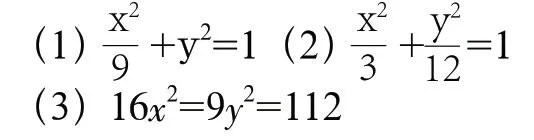
师：能帮我们总结一下求焦点的方法吗？

生15：先化成标准方程，再看分母大小确定焦点位置，再利用c=b-c求出，得到焦点坐标。

（评析：通过具体实例让学生能根据分母的大小判断焦点位置，会求椭圆方程中的基本量a,b,c的方法。）

变式：求适合下列条件的椭圆标准方程：

（1）焦 点 是F(-2,0)，F(2,0)且过点P(2,3)。（2）焦距为4，且过点P(2,3)。

师：对于（1），你能说出解题思路和主要过程吗？

生17：2a=PF+PF,直接求出a，c=2，b=a-c求出b。

（评析：掌握求椭圆标准方程常用的思想方法——定义法和待定系数法；求椭圆标准方程时，焦点位置不确定，能主动分类讨论。）

例2：已知一辆运油车上的储油罐截面的外轮廓线是一个椭圆，它的焦距为2.4m，外轮廓线上的点到两个焦点之和为3m，求这个椭圆的标准方程。(过程略)

（评析：与课程导入相呼应，解决实际问题。让学生能用数学的眼光观察世界，用数学的思维分析世界，让学生面对实际问题时，能用数学的思维去分析、建立模型并解决。）

教学反思：本课是圆锥曲线的方程的起始课，通过在课堂上让学生直观感受椭圆形状，判断椭圆的方法，让学生感受直观的不足、研究椭圆方程的必要，让学生的思维从具体到抽象，从浅层到深入，思维的发展可视化。在研究未知的椭圆方程时，引导学生回顾已学的圆的方程的求法，主动类比研究椭圆,培养学生数学建模意识。椭圆方程出来后,让学生从数与形两个角度感受对称性，体会数学形与数的统一，感受数学的美，让学生能在后续的双曲线中主动寻找数学的美，培养学生从数学的角度发现美并创造美的能力，感受大自然美的同时能尝试用数学建模的思想给予美的诠释。

数学是一种思维活动，数学教育是思维的教育。在知识的导入与生成过程中，通过设置高质量的问题，让学生充分思考，寻求思路的合理性，主动优化思路，让思维的增长有土壤，教师搭好脚手架，引导学生利用已有知识，在做中学，类比学，引导学生思维不断走向深入，提高学生数学素养。