基于组合式三系统估计量的人口普查净误差估计

胡桂华,文 婷,刘誉环

(重庆工商大学 a.数学与统计学院;b.经济社会应用统计重庆市重点实验室,重庆 400067)

一、引 言

在人口普查质量评估领域,研究净误差具有重要意义。净误差率是衡量一个国家或地区人口普查登记质量的核心指标。净误差率不足2%或超过5%表明普查登记质量较高或登记质量较低。净误差率也是修正普查登记人口数的主要依据。有些国家直接依据估计的净误差率修正普查登记人口数,也有些国家基于净误差率估计值和其他数据来源对普查登记人口数进行修正。因此,研究净误差具有重要意义。

净误差率计算的关键是估计总体实际人口数。目前大多数国家使用双系统估计量来估计它。但是,双系统估计量有一个内含交互作用偏差的“软肋”。研究表明,依据三次捕获模型构造的三系统估计量能够较好地解决双系统估计量的交互作用偏差问题。与双系统估计量所不同的是,三系统估计量并不要求三份人口名单必须独立,从而避免了人口名单之间不独立引起的交互作用偏差。

三系统估计量为不完整三维列联表7个已知单元的人口数和1个未知单元(未登记在任何一份名单的人口构成的子总体)的人口数估计量(称为缺失单元估计量)之和。缺失单元估计量依据7个已知单元的人口数来估计,其具体形式依据三份人口名单的统计关系确定。把这种模式下构造的三系统估计量称为普通三系统估计量,共有8种普通三系统估计量。

普通三系统估计量有两个局限性。一是在给出每种统计关系的普通三系统估计量的情况下,使用皮尔逊卡方统计量或对数似然比统计量,选择最适合于既定样本数据描述的普通三系统估计量。这两个检验统计量应用的前提条件是,构造每个已知单元的期望频数估计量。这是一项困难的工作。二是普通三系统估计量要么未利用7个已知单元信息,要么不加区分地对待每个信息。抽样推断理论指出,在构造总体参数估计量时,既要尽可能利用已知信息,还要根据信息的重要性确定其使用的次数。在总体中,同时登记在三份人口名单的人口所占比例最大,是最重要的信息,其在估计量中使用的次数应该最多;同时登记在两份人口名单的人口所占比例相对较少,是次重要的信息,其在估计量中使用的次数应相对少一些;而只登记在一份人口名单的人口更少,属于不重要信息,其在估计量中使用的次数应为最少。

为避免上述缺陷,提出组合式三系统估计量。通过研究,为政府统计部门使用三系统估计量提供更多选择。组合式三系统估计量的学术价值体现在两个方面。第一,它为7个已知单元的人口数与1个缺失单元的人口数估计量之和。缺失单元估计量的分子为三份人口名单同一类统计关系下的3个普通三系统估计量的分子之和,分母为它们的分母之和。在计算总体的组合式三系统估计量的抽样方差时,除了采用分层刀切法计算每一等概率人口层的抽样方差外,还要计算等概率人口层之间的协方差,否则低估或高估总体的组合式三系统估计量的抽样方差。第二,它须在等概率人口层建立,否则产生异质性偏差而影响其估计精度。

组合式三系统估计量的应用价值体现在两个方面。一方面,它省去了使用对数似然比选择最优组合式三系统估计量这一繁琐环节,便于在实际部门推广应用。对政府统计部门的实际工作人员来说,他们希望得到的是便于操作应用的、理论可靠的参数估计量。另一方面,它可以拓展到其他领域,解决其相关问题。例如,估计经济普查、农业普查的净误差率、户籍登记系统的覆盖率、老年人口数目估计。

创新之处体现在三个方面。第一,提出两种抽样登记的、人口移动的组合式三系统估计量,并在后面的实证分析中进行了抽样估计精度比较。第二,将抽样调查领域的分层二重抽样方法移植到人口普查净误差估计领域,解决其事后计数调查样本抽取及组合式三系统估计量各个单元估计量的构造问题。第三,厘清了普通三系统估计量与组合式三系统估计量的内在逻辑关系,这有助于读者理解和应用组合式三系统估计量。

二、文献综述

在捕获—再捕获模型基础上,美国学者增加了一次捕获,利用三次捕获的结果构造三次捕获模型[1-5];将三次捕获模型拓展到人口普查质量评估领域构造三份人口名单两种统计关系下的全面登记的普通三系统估计量[6]。孟杰等研究了普通三系统估计量及其统计性质[7]。胡桂华等研究了8种统计关系下的抽样登记的、人口移动的普通三系统估计量,为其应用于人口普查净误差估计奠定了理论基础[8-12]。

美国普查局2010年人口普查质量评估后,曾经打算在未来使用普通三系统估计量。美国普查局专家Griffin撰写了一篇这方面的研究论文,分析了双系统估计量低估总体实际人口数的主要原因在于,未包括同时倾向于遗漏普查与事后计数调查的人口,并且使用不完整三维列联表、最大似然估计和对数线性模型建立了三份人口名单各种统计关系下的普通三系统估计量[13]。后来由于未建立起覆盖人口总体范围广的行政记录系统,以及未进行大规模的试点研究,于是美国在2020年仍然使用双系统估计量。

中国原计划在2020年使用普通三系统估计量,后来由于三个原因放弃。一是普查名单和事后计数调查名单与户籍人口名单高度相似,即外表看起来是三份名单,其实是两份人口名单,从而失去了构建三系统估计量的意义[14]。二是尚未建立起科学完整的普查名单、事后计数调查名单与户籍人口名单的比对方案。在2020年,中国仍然使用在等概率人口层建立的双系统估计量[15]。三是中国并未建立起适合于普通三系统估计量所需要的复合人口行政记录名单。由于每份人口行政记录有其特定的用途和范围,因此建立中国的复合人口行政记录名单,不能只包括户籍名单,除该名单外,还要把常住人口名单,出生和死亡医学证明纳入其中,尤其是要把这些名单中的人具体落实到每一个样本普查小区。这项工作最好在普查标准时点前一个星期完成。复合人口行政记录名单最理想的截止时间是普查标准时点。这在实际中难以做到。丹麦、挪威和冰岛等北欧国家的行政记录截止日在普查时点前一个星期。

研究组合式三系统估计量的意义在于,将利用信息量不足的若干普通三系统估计量组合在一起,构造出一个新的三系统估计量,从而间接利用了多个信息,避免了普通三系统估计量的缺陷。建立三系统估计量的初衷就是要尽可能多地使用多个信息来源。利用更多相关信息,有助于提高估计精度。从这个角度看,组合式三系统估计量具有研究价值,有助于提高净误差的抽样估计精度。

三、组合式三系统估计量及其相关理论

(一)全面登记的双系统估计量及普通三系统估计量

我们首先依据三次捕获模型要求,构造事后计数调查对总体全面登记的普通三系统估计量。这么做的理由是,普通三系统估计量来源于三次捕获模型。三次捕获模型是在三次全面捕获的情况下构造的。

普通三系统估计量由双系统估计量拓展而来。为便于推导普通三系统估计量公式,简要介绍一下双系统估计量是有必要的。构造双系统估计量的重要工具是不完整二维列联表。在假设总体中的每一个人有同样的概率登记在普查的情况下,总体中的人口在普查与事后计数调查中的登记情况列示在该表中,见表1。

表1 不完整二维列联表

在表1中,右下脚标1表示登记在普查或事后计数调查中,0表示未登记在普查或事后计数调查中。在假设总体人口有同样的概率登记在普查或事后计数调查,以及事后计数调查对总体全面登记情况下,估计总体规模的双系统估计量(Dual System Estimator,DSE)为:

(1)

从式(1)可以看出,x11,x10,x01是已知单元人口数,而x00是未知单元人口数,需要估计。未知单元的人口数可以通过式(2)来估计:

(2)

为便于普通三系统估计量的建立,需要将总体中的人口在三份人口名单的登记情况列示在不完整三维列联表,见表2。

表2 不完整三维列联表

在表2中,xijk中的右下脚标i,j,k为示性变量,均取值1或0,1表示在普查登记中,0表示不在普查登记中。除最后一个单元(ijk)=(000)的x000需要估计外,其他单元的人口数都是可以观察到的。

如果不存在比对误差,两项调查和人口行政记录均是对同一总体的全面登记,总体人口有同样概率登记在普查的情况下,那么估计总体规模的普通三系统估计量(Triple System Estimator,TSE)为:

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(二)全面登记的组合式三系统估计量

全面登记的组合式三系统估计量为7个已知单元的人口数与组合式缺失单元估计量之和。

1.全面登记的、无人口移动的组合式三系统估计量

不难看出,式(4)至式(6)属于同类统计关系,而式(7)至式(9)属于另一类统计关系。式(4)至式(6)存在的问题是,对7个已知单元的信息给予同样的关注,赋予同样的权数1。式(7)至式(9)只是使用了7个已知单元信息中的3个,使用的信息量过少,必然影响估计精度。针对这种情况,可以构造两种组合式缺失单元估计量。一是将式(4)至式(6)的分子和分母分别相加,得到组合式三系统估计量式(10);二是将式(7)至式(9)的分子和分母分别相加,得到组合式缺失单元估计量式(11)。

(10)

(11)

将式(10)和式(11)分别代入式(3),得到两种组合式三系统估计量,见式(12)和式(15)。

(12)

(13)

(14)

(15)

(16)

(17)

式(1)至式(17)未考虑普查标准时点与事后计数调查标准时点之间的人口移动(不包括出生和死亡者)。但实际上,这两个标准时点之间不可避免有人口移动。有三种移动人口:一是无移动人口(Non-movers,缩写为n),即普查标准时点和事后计数调查标准时点之间一直居住在本普查小区的人口。二是向内移动人口(In-movers,缩写为i),即普查标准时点居住在其他普查小区,在事后计数调查标准时点前来到本普查小区的人口。三是向外移动人口(Out-movers,缩写为o),即普查标准时点在本普查小区,事后计数调查标准时点前离开本普查小区的人口。事后计数调查人口构成有两种方法:一是A构成方法,由无移动人口和向外移动人口构成。二是B构成方法,由无移动人口和向内移动人口构成。

对式(12)至式(17),均构造两种方法下的人口移动的组合式三系统估计量。此时,式(12)至式(17)中每个单元涉及事后计数调查的项一律变为两项。考虑到向内移动人口不可能出现在本普查小区的行政记录人口名单中,因为其普查标准时点在其他小区,而不在本小区,因此向内移动人口涉及到的人口行政记录的项一律为零,例如x111i=0。另外,向外移动人口不可能登记在本小区的事后计数调查人口名单中,因为事后计数调查标准时点时不在本普查小区,因此向外移动人口涉及事后计数调查的项一律为零,例如x011o=0。

2.式(12)至式(14)全面登记的、人口移动的组合式三系统估计量

如果采取A构成法,那么式(12)至式(14)变为:

(18)

x1,A=x111n+x111o+x110n+x110o+x101n+x101o+x100n+x100o+x011n+x011o+x010n+x010o+x001n+x001o

(19)

由于x111o=x110o=x011o=x010o=0,因此式(19)变为式(20):

x1,A=x111n+x110n+x101n+x101o+x100n+x100o+x011n+x010n+x001n+x001o

(20)

(21)

如果使用B构成法,那么式(12)～(14)变为:

(22)

x1,B=x111n+x111i+x110n+x110i+x101n+x101i+x100n+x100i+x011n+x011i+x010n+x010i+x001n+x001i

(23)

由于x111i=x101i=x001i=x011i=0,因此式(23)变为:

x1,B=x111n+x110n+x101n+x100n+x011n+x010n+x001n+x010i+x100i+x110i

(24)

(25)

3.式(15)至式(17)全面登记的、人口移动的组合式三系统估计量

如果采取A构成法,那么式(15)至式(17)变为:

(26)

x2,A=x111n+x111o+x110n+x110o+x101n+x101o+x100n+x100o+x011n+x011o+x010n+x010o+x001n+x001o

(27)

由于x111o=x110o=x011o=x010o=0,因此式(27)变为式(28):

x2,A=x111n+x110n+x101n+x101o+x100n+x100o+x011n+x010n+x001n+x001o

(28)

(29)

如果使用B构成法,那么式(15)至式(17)变为:

(30)

x2,B=x111n+x111i+x110n+x110i+x101n+x101i+x100n+x100i+x011n+x011i+x010n+x010i+x001n+x001i

(31)

由于x111i=x101i=x001i=x011i=0,因此式(31)变为:

x2,B=x111n+x110n+x101n+x100n+x011n+x010n+x001n+x010i+x100i+x110i

(32)

(33)

(三)抽样登记的组合式三系统估计量

事后计数调查是对样本普查小区人口的抽样登记[16-18]。这决定了只能建立抽样登记的组合式三系统估计量。这项工作分为两个步骤,第一步是在全面登记的组合式三系统估计量基础上,写出抽样登记的组合式三系统估计量。第二步是采用有限总体概率样本数据,构造抽样登记的组合式三系统估计量每个单元人口数的估计量。

1.式(12)至式(14)抽样登记的、人口移动的组合式三系统估计量

如果采取A构成法,那么:

(34)

(35)

(36)

如果使用B构成法,那么:

(37)

(38)

(39)

2.式(15)至式(17)抽样登记的、人口移动的组合式三系统估计量

如果使用A构成法,那么:

(40)

(41)

(42)

如果使用B构成法,那么:

(43)

(44)

(45)

(46)

在式(46)中,yhgi表示层hg的最终进入第二重样本的普查小区i在三份人口名单登记的人口数,例如同时在三份人口名单登记的无移动人口数x111n,在普查中登记但未在事后计数调查和人口行政记录登记的向外移动人口数x100o;H为第一重抽样前对总体普查小区划分的总层数,h为任意层;G是对第一重样本普查小区进一步划分的总层数,g是任意层;xhgi为层h的样本普查小区是否在层g的示性函数,如果在,xhgi=1,否则xhgi=0;Ihgi为层hg的第一重样本普查小区是否进入第二重样本的示性函数,如果进入了,Ihgi=1,否则Ihgi=0;αhgi为第i样本普查小区经过二重抽样后进入到第二重样本的最终抽样权数。如果样本答复率不足100%,则要根据样本答复率调整初始抽样权数。调整的办法是,将初始抽样权数除以样本答复率。在后面的实际案例中,样本答复率为100%。

如果层h的普查小区总数为Nh,样本普查小区数为nh,层hg的普查小区总数为Mhg,样本普查小区数为mhg,并且每重抽样采取简单随机抽样,每重抽样的抽样单位均为普查小区,那么经过两重抽样后,第i样本普查小区的最终抽样权数αhgi=(Nh/nh)(Mhg/mhg)。

注意式(34)至式(45),需要在等概率人口层v建立。这里只是为了书写便利,才在式(34)至式(45)中省去了v记号。在建立了等概率人口层v的组合式三系统估计量之后,还要建立总体的抽样登记的、人口移动的组合式三系统估计量,用P表示总体:

(47)

(48)

(49)

(50)

(四)抽样登记的、人口移动的组合式三系统估计量的抽样方差估计

式(34)、式(37)、式(40)、式(43),以及式(47)至式(50)是较为复杂的估计量,其抽样方差使用刀切法近似计算。刀切法实施的关键是复制权数的计算[19-20]。复制权数是指每剔除第一重样本中的一个样本普查小区后重新计算的进入第二重样本普查小区的抽样权数。

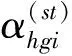
(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

等概率人口层抽样登记的三系统估计量的刀切抽样方差估计量为:

(62)

(63)

(64)

(65)

总体的抽样登记的三系统估计量的刀切抽样方差估计量为:

(66)

(67)

(68)

(69)

(五)总体的人口普查净误差估计

(70)

(71)

(72)

(73)

在式(70)～(73)中,Cp是总体的、已知的最终普查登记人口数,其抽样方差为零。从式(70)～(73)可以看出,只要估计了总体的实际人口数,将其减去普查登记人口数,便可以很方便地估计人口普查净误差,并且两者的抽样方差相等。

四、实证分析

(一)基本信息及样本数据

为计算人口普查净误差,在实证分析中,应该获得实证范围内普查年样本普查小区人口的微观资料、各个等概率人口层的普查登记人口数。然而,我们没有得到这样的数据,只是获得了非普查年某行政区的相关资料。根据这些相关资料,可以估计总体实际人口数,而总体实际人口数的估计是净误差计算的关键。从这个意义上来看,在净误差估计中,非普查年的微观资料还是有使用价值的。

实证资料来源于某行政区的20个样本普查小区的三份人口名单。时间为2017年8月31日。研究采取分层二重抽样方法,在第一重抽样前,将其所有普查小区分在两层:街道层共有1 970个普查小区,记为h=1和N1=1 970;镇层共有1 068个普查小区,记为h=2和N2=1 068。这两层总共有普查小区3 038个,记为N=3 038。对h层样本普查小区,进一步按照调查难度分为三层:调查难度大层,记为g=1;调查难度中等层,记为g=2;调查难度小层,记为g=3。在每重抽样中,以普查小区为抽样单位,简单随机不重复抽取样本。样本形成过程见表3,样本数据见表4至表7。

总体人口划分在四个等概率人口层:0～64岁男性;0～64岁女性;65岁及以上男性;65岁及以上女性。

(二)基于组合式三系统估计量的估计结果

利用表3至表7样本数据,以及使用式(34)至式(69),得到等概率人口层及总体实际人口数的估计值及其抽样标准误差估计值,见表8。从表8可以得到如下重要信息。

表3 样本形成、样本量和抽样权数

第一,表8提供了4个等概率人口层及总体的实际人口数及其抽样标准误差估计值。各个等概率人口层的实际人口数使用组合式三系统估计量估计。组合式三系统估计量不能直接用来估计总体的实际人口数。总体的抽样标准误差不是四个等概率人口层的抽样标准误差之和,而是四个等概率人口层的抽样方差之和及它们之间协方差2倍之和总和的平方根。

第二,使用两种组合式三系统估计量估计的总体实际人口数在77万人左右。按照中国平均每个普查小区250人常住人口来算,本行政区的3 038个普查小区的人口数应为759 500人。可见,两种组合式三系统估计量估计的结果与现实情况基本吻合,是有效的三系统估计量。如果把759 500人视作普查登记人口数,那么基于A构成法的第一个估计量估计的实际人数为769 339人,净误差为9 839人,净误差率为1.27%,这也属于合理估计值。

第三,对同一种组合式三系统估计量,使用A构成法和B构成法得到的估计结果不尽相同。如果采取第一种组合式三系统估计量,两种构成法提供的人口数估计值分别为769 339人和773 742人。采取第二种组合式三系统估计量,这两种构成法提供的人口数估计值分别为770 212人和775 640人。A构成法直接提供的是普查标准时点的人口数估计值,与人口普查净误差对普查目标总体实际人口数估计值的要求一致,但找到向外移动人口有比较大的困难。B构成法虽然也是提供普查标准时点的人口数估计值,但它是通过向内移动人口回忆普查标准时点的情况得到的,可能发生回忆误差。不过B构成法也有其优势,那就是向内移动人口在本样本普查小区,不存在寻找人的问题,调查方便。因此,两种构成法各有利弊,需要进行选择。为了更好实现净误差估计目标,应该选取A构成法。为便于调查,则选取B构成法。在实际应用中,选取A构成法是合适的。

表4 0～64岁男性层各单元的常住人口数单位:人

表5 0～64岁女性层各单元的常住人口数单位:人

表6 65岁及以上男性层各单元的常住人口数单位:人

表7 65岁及以上女性层各单元的常住人口数单位:人

表8 基于组合式三系统估计量的人口数及其抽样标准误差估计值 单位:人

(三)组合式三系统估计量与普通三系统估计量的抽样估计精度比较

表9 组合式三系统估计量与普通三系统估计量的比较 单位:人

从表9可以看出:

第一,两个组合式三系统估计量估计的总体实际人口数分别为769 339人和773 742人,而普通三系统估计量估计的总体实际人口数为766 859人。如果普查登记人口数为759 500人,那么两个组合式三系统估计量和普通三系统估计量估计的人口普查净误差分别为9 839人、14 242人和7 359人。这说明,由于利用的信息量不足,普通三系统估计量低估总体的净误差。组合式三系统估计量能避免低估总体净误差。

第二,从总体实际人口数估计值的抽样标准误差来看,两个组合式三系统估计量的抽样标准误差分别为5 018人和5 301人,而普通三系统估计量的抽样标准误差为5 390人。这意味着,组合式三系统估计量比起普通三系统估计量拥有更高的估计精度。

第三,从各个等概率人口层实际人口数估计值的抽样标准误差来看,除0～64岁男性层外,两个组合式三系统估计量的其他所有等概率人口层的抽样标准误差均小于普通三系统估计量。例如,0～64岁女性层,两个组合式三系统估计量的抽样标准误差分别为1 910人和1 630人,而普通三系统估计量实际人口数估计值的抽样标准误差为1 932人。这表明两个组合式三系统估计量更适合于等概率人口层实际人口数的估计。

五、结 论

第一,组合式三系统估计量是在普通三系统估计量的基础上建立起来的,是一个全新的三系统估计量。与普通三系统估计量不同的是,它是把三份人口名单同一类统计关系下的三个普通三系统估计量的缺失单元估计量的分子和分母分别相加得到的。与普通三系统估计量相同的是,它的7个已知单元的人口数与普通三系统估计量的相同。

第二,组合式三系统估计量须在等概率人口层建立。为此,需要选择变量对总体分层。在选择分层变量时,要考虑到变量值能否获得。个人性格虽然是影响人们是否参与人口普查的重要变量,但很难知悉一个人的性格,因此不应该把性格作为对总体人口分层的重要变量。

第三,刀切法适合于组合式三系统估计量的抽样方差计算。组合式三系统估计量利用的是样本资料,需要计算其抽样方差。由于估计量结构复杂,无法用代数方法直接计算其方差。然而,不能因此就放弃了方差的计算。用分层刀切法近似计算这个方差是可行的。

第四,组合式三系统估计量对实际人口数的估计精度高于普通三系统估计量,希望被政府统计部门采纳及推广应用。