铁路应急设施非概率可靠性选址优化研究
汤兆平, 孙剑萍
(华东交通大学 信息工程学院,江西 南昌 330013)
0 引言
应急设施科学选址是保障应急资源快速、安全、顺畅地送达事故点,充分发挥铁路应急救援系统的各项功能,最小化突发事件带来损失与影响的基础。然而,受交通路况、气候变化、道路受损、车辆状况等因素影响,应急路网上的路段阻抗(如距离、时间等)往往是不确定的,其参数的变化和波动对选址决策影响较大。铁路应急设施选址具有高度战略性、建设成本高昂以及中长决策期的特点,应最大程度规避各种不确定因素波动引起的风险,有必要考虑区间阻抗的不确定性,开展可靠性选址优化研究。现有基于可靠性理念的选址优化研究主要集中于概率和模糊方法。
基于概率方法,于冬梅等[1]考虑设施中断概率,研究了加固预算及最大最小容量限制下的可靠性应急设施选址优化。尹小庆[2]借助在规定时间内物资从配送站配送至需求点的概率描述行程时间可靠性,提出了一种配送站选址方法。陈贵景[3]将车速视为区间上取值的随机数,提出物资运送时间不迟于规定时间的多目标非线性选址-路径模型,基于加权排序的遗传算法求解,提高了紧急救援时间的可靠性。范厚明[4]在内陆多式联运网络中,利用路径失灵概率刻画系统的可靠性,研究了内陆港的随机选址问题。魏宗田[5]考虑路网潜在的失效边及其失效概率,提出了综合集合覆盖、p-中值和无容量限制固定费用选址三个经典问题的设施可靠性选址方法。郭咏梅[6]考虑遍历不同数目失效设施的多种情形下的概率,综合应急设施可靠性要素进行了选址优化。万波[7]基于M/M/c排队系统,建立了需求随机条件下基于时间效率的设施选址模型,满足了行程时间可靠性。Yavari[8]考虑线路中断、价格敏感需求的随机性,探索了易腐品的多周期选址、库存、路径方法。Haghjou[9]基于场景的鲁棒方法,处理供应链网络设计问题内在的需求周期变化和设施中断的随机不确定性,提出了动态鲁棒可靠性选址方法。Aboutahoun[10]基于最大化从随机树网络节点到设备的最小加权可靠性的最优准则,研究了设施选址的建模及求解。Zhong[11]考虑非线性车辆容量约束,建立双目标整数非线性规划模型,实现了随机需求下的灾害救援设施选址与车辆路径的风险规避优化。Yun[12]研究了不完全信息下每个设施破坏概率随空间而异的可靠设施选址问题的建模方法,并确定了可靠性选址方案。
基于模糊方法,刘虹[13]采用模糊隶属度刻画客户对配送服务的满意度,在能力和载重等约束下进行多目标选址路径规划,保障了选址方案下路径配送时间的可靠性。于冬梅[14]考虑需求点对应急服务质量满意度的异质性,基于模糊覆盖函数,建立服务能力有限的可靠性应急设施选址优化模型,并给出Pareto最优解集的三维空间分布。Hamidreza[15]将需求、设施成本和库存成本等不确定因素作为三角模糊数,提出了一种基于被动防御的不确定性下的供应链选址、库存、路径的可持续多目标模型,提高了供应链应对环境变化的可靠性。Gharib[16]考虑基础设施破坏的影响,以人工神经模糊推理系统对模型输入进行预处理,使用决策技术和图论寻找安全路径,解决了最小化运输时间和最大化可靠性目标下的应急车辆路径选址问题。Mohammadi[17]针对需求、设施容量、杂项成本和运输时间等的模糊不确定性,研究了救援链设施可靠选址及救济品配送路径问题。Tirkolaee[18]基于模糊机会约束规划方法,建立了一种新的混合整数线性规划模型,用于解决COVID-19大流行期间医疗废物管理的选址-路线问题,保障了感染性医疗废物处理的可靠性。
铁路突发事件发生的概率相对较低,属于小样本事件;救援网络通达路径单一,极易造成救援不可靠;应急设施建设成本昂贵,应急资源具有行业专属性;一旦发生事故,社会影响大,更强调救援的强时效性。针对以上铁路应急救援的特殊性,当前文献主要存在以下不足:一方面,概率、模糊的方法均建立在严格的数学理论基础上,前者采用客观概率,后者采用主观概率,应用时须事先获知不确定参数的概率分布型式或作出可行的主观分布假设,对大量原始数据具有高度依赖性,在小样本、贫信息问题研究中存在局限性。另一方面,铁路应急救援的强时效性要求,不仅期望尽可能地减少应急时间,同时还期望应急时间具有强稳定性。
本文创新性地将选址-路径问题与区间非概率可靠性方法结合起来,采用区间数刻画路段时间阻抗,提出路径的非概率可靠性度量及可靠最短路径选择方法,建立可靠最短路径的无容量设施的选址优化模型,并提出约束条件限制的Monte Carlo改进求解算法。结合实例,与已有文献研究结果进行比较和分析,验证了模型和算法的有效性,为铁路应急设施的可靠性选址提供了理论指导和决策支持。
1 应急需求点与路段阻抗的区间特性
各类突发事件侵袭铁路路网的事故确切点通常难以准确预测,即使对于一起已经明确具体位置的突发事件,事故影响区域往往也是具有一定长度的区段。再加上铁路的区间性管理特性,突发事件对铁路的影响具有区间性。因此,可将铁路路网的节点定义为具有一定取值范围的区间点(图1)。此外,在突发事件发生时,救援前准备、天气条件、道路受阻程度等都存在强不确定性,导致应急资源从储备点运送到各需求点所经过的距离或运行时间(路段阻抗)也存在不确定性,且通常无法通过大量统计信息准确描述其分布特征或明确优势隶属度函数。然而实际救援中,获取路段阻抗的变动范围却较容易,故引入区间数学,将路段阻抗视为区间数,以更好地表征其不确定性。区间数学的基本思想是应用区间变量代替点变量进行计算。其特点是用区间数表达变量,经区间运算获得的区间范围,可包含计算结果的所有可能取值,这就为铁路路网节点、边及路径的权重进行区间分析提供了严谨的数学基础。
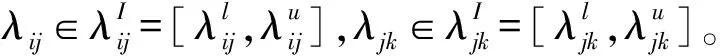
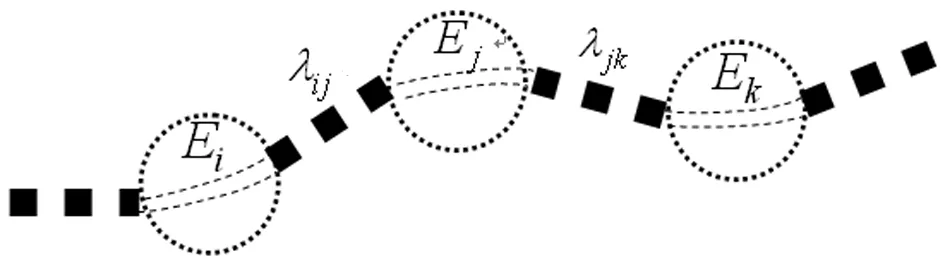
图1 铁路路网节点的区间性
2 区间模型非概率可靠性指标的定义
非概率可靠性最早于二十世纪九十年代初,由以色列洪堡学者Yakov Ben-Haim和美国Florida大西洋大学Isaac Elishakoff教授提出,它在掌握数据信息较少的情况下,对分析系统可靠性有明显优势,已在航空航天、桥梁结构、岩土工程、机械工程等领域得到应用,其中区间模型非概率可靠性方法应用最为广泛。
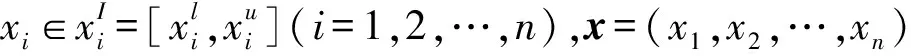
M=g(x)=g(x1,x2,…,xn)
(1)
g(x)=0的超曲面称为功能失效面;g(x)<0和g(x)>0分别表示功能处于失效和可靠状态。
当g(x1,x2,…,xn)为xi(i=1,2,…,n)的连续函数时,M为一区间变量。设其中心和半径分别为Mc和Mr,并令
η=Mc/Mr
(2)
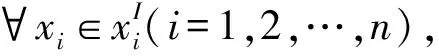
考虑到功能对输入参数的响应,设已知功能响应的许用区间为:
y∈yI=[yI,yu]
(3)
再设功能对输入参数的响应函数为:
f(x)=f(x1,x2,…,xn)
(4)
则功能方程为:
M=g(x,y)=y-f(x)=y-f(x1,x2,…,xn)
(5)
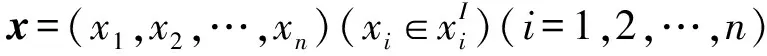
(6)
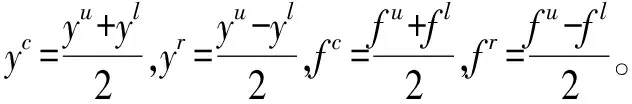
3 路径时间非概率可靠性指标的确定
3.1 时间非概率可靠性指标的度量
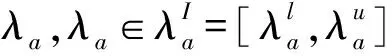
引入区间模型可靠性理论[19],应急开始时间可靠性可描述为应急开始时间t小于等于最长应急响应时间限制期T的可能性。定义通过路径PL进行救援,应急开始时间不超期(即t≤T)的功能函数M为:
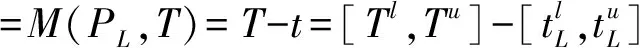
(7)
根据失效准则,M=0(即T=t)称为应急救援时间的失效面,M<0(即T
M为区间变量,区间中心
(8a)
区间半径
(8b)
并令
η=Mc/Mr
(8c)
式(8c)为区间模型时间可靠性指标的广义定义。当η>1,总有M>0,此时,救援时间充裕,救援应急时间完全可靠;当η<-1时,M<0,救援应急时间一定超限(失效);当-1≤η≤1时,可能出现M<0和M>0两种情况,表明救援时间不一定可靠。随着η值越大,救援时间不超限(可靠)的可能性会越来越高。根据式(7)和式(8c),可靠性指标η还可表示为:
(9)
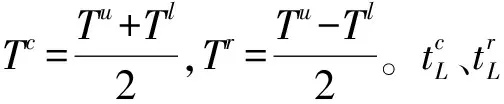
当T为常数T0时,即Tl=Tu=T0,此时通过路径PL不超出时间限制T0的可靠性指标η为:
(10)
3.2 路径时间可靠性指标的计算
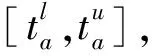
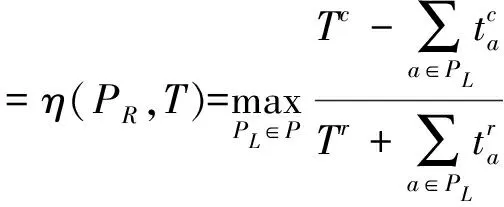
(11)
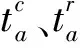
当T为常数T0时,路径PR的最大应急时间非概率可靠度指标为:
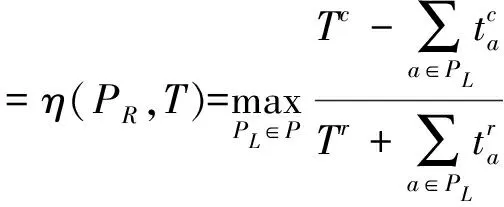
(12)
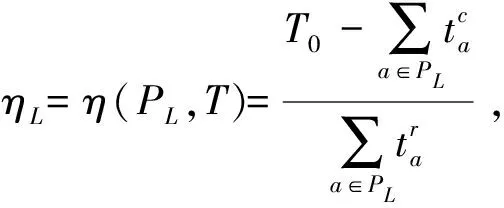
(13)
由公式(13)可见,η的大小,取决于救援途经的每段边弧上所花费时间的上下界与最长应急时间限制期的取值。为简化运算过程,引入一个自变量为η的函数N(η),作为路网中任意两区间点Ek、Ej之间路径的基于时间可靠性指标的阻抗,以下简称为等效时间阻抗。
考虑到对于一条路径或一个路段而言,其时间区间下界值的物理含义可理解为路段非延误状态下的阻抗,上界值则可理解为路段延误状态下达到的最大阻抗。当时间充裕时,救援过程中允许时间取上界值,而若实际运行中所花时间短于上界值,结果还将更可靠,相反,若时间不够充裕时,救援过程中每个环节必须更加紧凑,所花时间应尽可能偏于下界值。故对函数N(η)设计如下:
(14)
式(14)可以看出,N(η)的值越小,经由该路径救援时,应急开始时间越可靠。为保证救援时间可靠,应尽量搜索N(η)取值最小的路径。
将PL(η)视为Ek、Ej之间的时间可靠性路径。随着η的变化,当某救援路径具有最小的N(η)(即N(η)=N(η*))时,该路径就是Ek、Ej之间取得最大的时间可靠性指标的路径PR,简称为可靠最短路径。路网中各节点之间的可靠最短路径矩阵可表示为:
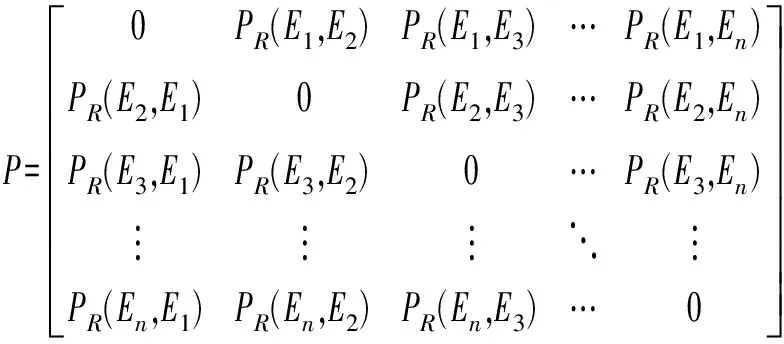
(15)
该路径PR的等效时间阻抗矩阵为:
(16)
4 可靠最短路径下的铁路资源储备点选址优化
4.1 问题描述
设某铁路路网为拥有m个节点的无向赋权网络G,节点E={E1,E2,…,Em}为所有需求区间点,节点权重系数分别为ωEj(j=1,2,…,m)。连接任意两个节点Ek、Ej的所有路径中可靠最短路径为PR(Ek,Ej),该路径所对应的最大时间可靠性指标为η*(PR,T)。路网中任意一点Sφ到任意一需求点Ej的边阻抗为等效时间NR(Sφ,Ej)。现需在各备选点未知的情况下,合理确定n(n≥1)个资源储备点的布设方案Φ={S1,S2,…,Sn}。在最长应急时间限制期T内,使所有储备点与需要其提供服务的需求点之间的连接路径的节点加权等效时间之和最小以及服务半径最小。
4.2 模型建立
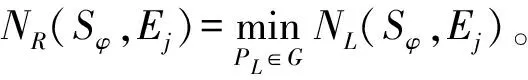
(17)
模型中ω1与ω2分别为两个分目标的权重。第1个约束条件表示经由任意两节点所选路径为可靠最短路径;第2个约束条件表示储备点Sφ到其所服务的需求点Ej的等效时间NR(Sφ,Ej)满足时间限制期T约束;第3个约束条件表示每个需求点仅由一个储备点提供服务;第4个约束条件表示储备点的个数恰好为n;第5个约束条件表示n个储备点从路网G的备选点集合Sφ中选取;第6个约束限定决策变量xφj为0-1变量,若Sφ为Ej提供服务,则xφj=1,否则xφj=0。
4.3 模型求解算法设计
4.3.1 路网等效时间矩阵及路径矩阵的算法
结合本文提出的最大的应急时间非概率可靠度的概念,改进文献[20]中的算法,任意两个节点之间的等效时间矩阵NR、可靠最短路径矩阵LR的具体算法步骤如下:
步骤1令θ=1,计算并得出初始等效时间矩阵为NR、初始可靠最短路径矩阵为LR;
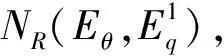
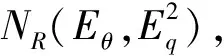
(18)
(19)
……
(20)
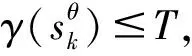
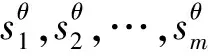
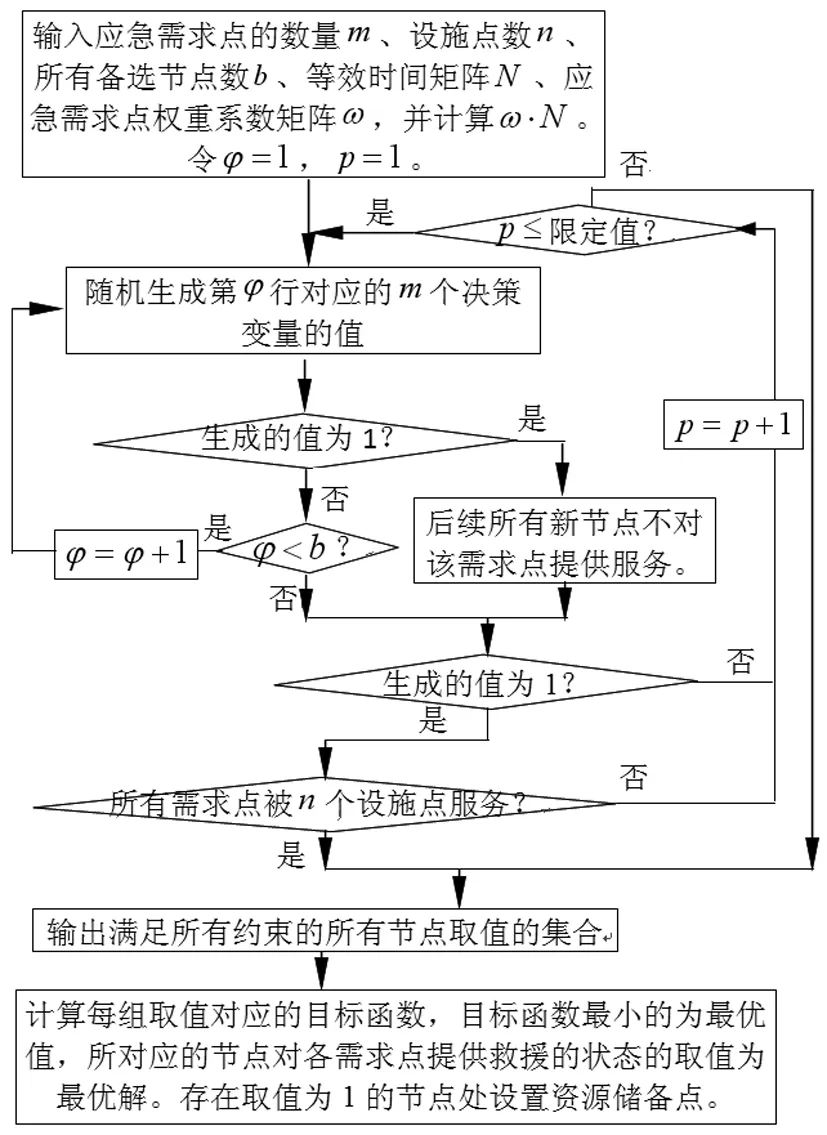
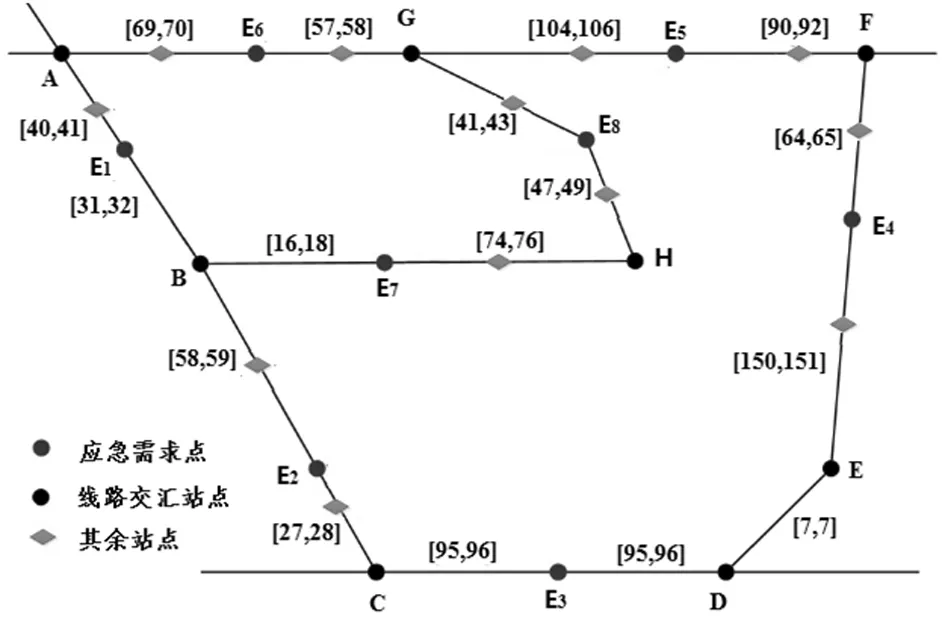
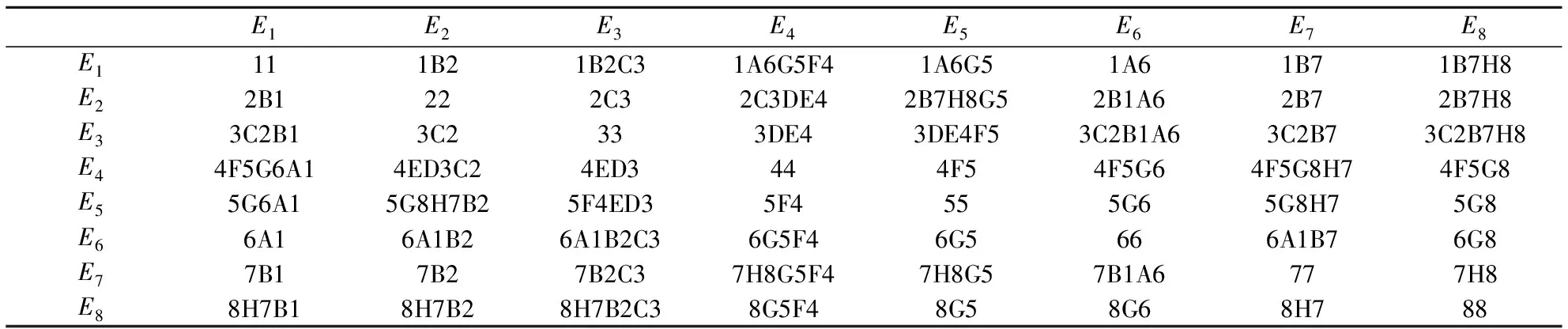
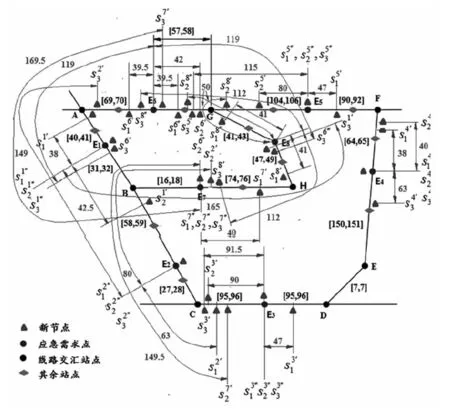
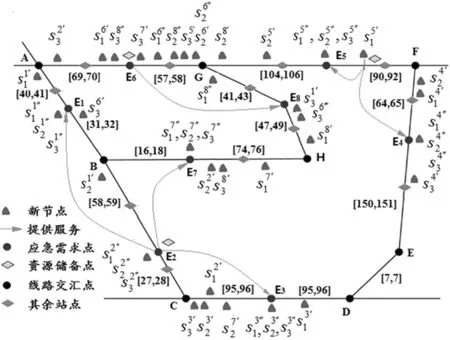
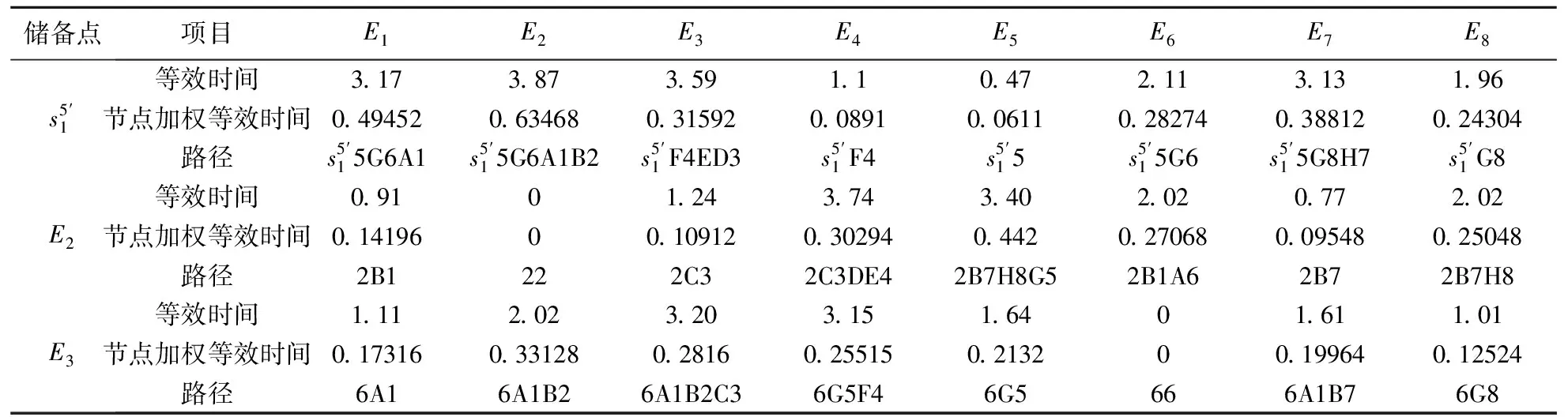
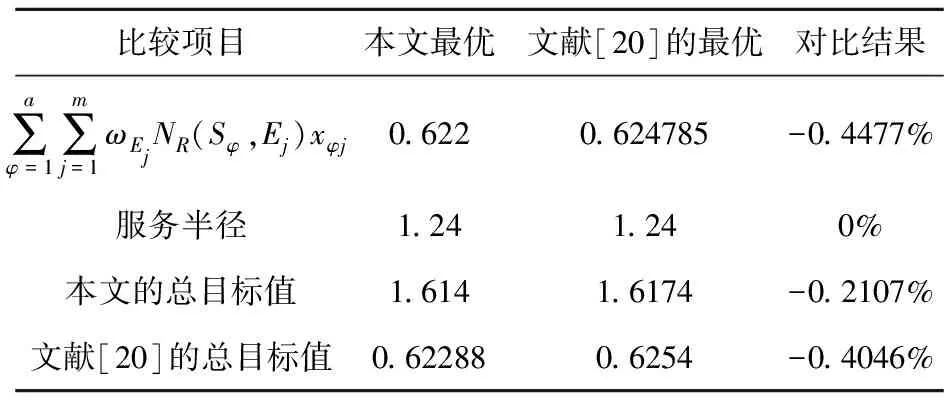
步骤6若θ 4.3.2 约束条件限制的Monte Carlo选址算法 4.1节中提出的无容量设施选址问题(Uncapacitated Facility Location Problem, UFLP)本质上是个组合优化问题。由于所有节点(包括新、旧节点)对各需求点是否实施救援的状态仅有两种:0(不救援)或1(救援)。如以新、旧节点总数为40,需求点为8个来看,将是一个40行8列的矩阵,其取值的可能性有2320=2.13599×1096种。这种数据计算量,即使对于大规模实际问题求解具有优势的Monte Carlo方法,几乎也庞大得无法想象。而且Monte Carlo每次随机生成的数据都相互独立,无法获得满足所有约束条件的、有效的矩阵数据组,更不用说从里面搜索出最优。 本文提出基于约束条件限制随机生成可行解的Monte Carlo方法(图2),在随机变量生成过程中,不断用约束条件进行限制,使生成的矩阵数据组尽可能符合所有约束条件,以增加随机产生矩阵数据组的有效性,从而实现在大量的可行解中寻找最优,加快寻优速度。 图2 约束条件限制的Monte Carlo选址算法流程图 具体思路:以所有节点为行,需求节点为列,xφj表示第φ行节点对第j列需求节点提供服务的状态;设定循环次数p的最高限定值,随机生成第一行的m个决策变量的值(0-1值)。根据公式(17),第3个约束条件对后续对应列的决策变量的取值进行限定,若前面行中该列存在决策变量取值为1,则后续行所在列均取值0(确保每列只有一个1),否则随机生成其值;根据第4个约束条件要求,资源储备点的个数恰好为n,须在随机生成后续值的时候进行检验,确保输出所有节点取值的集合满足所有约束。 可以证明,以Monte Carlo直接计算UFLP问题,算法的时间复杂度为指数阶O(2n),而以本文提出算法,改进了常规Monte Carlo法无法控制变量生成值的缺陷,增加了仿真的有效率,算法的时间复杂度仅为平方阶O(n2)。在计算问题规模较大的情况下,本文提出的方法具有更小的时间复杂度,算法的执行效率也更为理想。 为验证本文模型的适用性、完整性及算法的运算能力,并便于与已有文献研究进行比较,选用文献[20]的算例,即中国铁路济南局集团有限公司的胶济线、京沪线、新日线、胶新线、临泰线五条线路构成的路网为例。该局拟于青杨、吴村、平邑、诸城、潍坊东、郭店、黑旺和燕家庄8个需求点(分别以E1~E8表示,在路径表达时简化为阿拉伯数字1~8)中建立3个资源储备点。基于铁路线路里程表和应急平台基地地理信息,路网抽象如图3所示。 图3 路网选址模型抽象图 图中字母A~H分别表示各条线路的相交站点:济南、泰山、兖州、临沂、临沂北、胶州、东风、常庄。设最大救援响应时间T=2.5h,在途平均速度v=100km/h。ω1=1和ω2=0.8。要求若任一需求点出现突发事件时,必须且仅需其中的1个储备点在时间期限内对其实施救援,实现前述的双目标最优。 根据历史突发事件次数、应急点的区间长度、应急点对路网连通重要度三方面指标及数据,代入式(21),计算得到各节点的权重(表1)。 (21) 式中,x1j,x2j,x3j分别是节点的三方面指标及数据的量化取值;μ1,μ2,μ3分别是三方面间的相对权重系数。 表1 应急需求点权重值 5.2.1 构建初始距离矩阵 利用Floyd矩阵算法,得到所有需求点间最短距离矩阵。依据本文算法,由公式(16)得到路网等效时间矩阵NR(表2,单位:h);并回溯得到可靠最短路径矩阵LR(表3,单位:h)。 表2 等效时间矩阵NR(单位:h,T=2.5h) 表3 可靠最短路径矩阵LR 表4 E1~E8局部中心半径 图4 路网选址模型新节点位置示意图 图5 本文模型设址及服务情况 5.2.2 局部中心点和绝对中心点的计算 按照局部半径、局部中心点的定义及前述算法,通过MATLAB编程计算,共获得24组新节点集合及其在路网中的位置,如图4所示。 整理计算数据,得到各选定的储备点与需求点间路径的相关信息如表5所示。 表5 储备点与需求点间路径等效时间、节点加权等效时间、路径 现将本文的最优解分别与文献[20]的最优解进行比较,结果如表6所示。 表6 本文与文献[20]选址方案比较分析 通过以上分析和比较,得出以下结论: ①以本文的优化总目标看,本文较文献[20]方案总目标值从1.6174下降至1.614,下降了0.2107%;以文献[20]的总目标看,本文较文献[20]方案总目标值从0.6254下降至0.62288,下降了0.4046%,证明本文的选址方案更优。另外,节点加权等效时间之和下降了0.4477%,表明本文方案能更好地保证救援应急时间可靠性。 ②本文提出的基于约束条件限制随机生成可行解的Monte Carlo算法,改进了常规Monte Carlo方法无法控制最终得到的变量生成值的缺陷,时间复杂度由常规方法的指数阶改进为平方阶,大大改进了算法在大规模下问题的执行效率。经实例验证,对本文算法中的100000次迭代采用计数方式计算,其中有50000左右的数据满足所有约束条件,有效数据率高达41.51%~57.42%,减少了计算量和运算时间。 铁路应急资源储备点的选址与普通物流设施选址的主要区别在于应充分考虑救援的时间可靠性,确保灾后尽快展开救援。本文创新性地引入区间非概率可靠性理论,提出路径行程时间的非概率可靠性度量及可靠最短路径选择方法;建立基于区间时间阻抗下可靠最短路径的无容量设施选址模型;提出约束条件限制的改进算法。实例结果表明:本文方案在各项指标上均优于文献[20]的最优结果。提出的改进算法提高了仿真有效率,缩短了运算时间。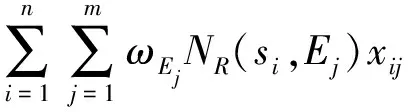
5 算例分析
5.1 算例概况

5.2 相关初始数据矩阵计算


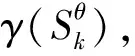
5.3 新节点集合及位置确定
5.4 模型的求解
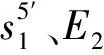
5.5 算例分析与比较
6 结论

