极端损失条件下分组群体的主观概率累积偏差仿真研究
张 羽, 刘 伟, 谯 丽, 岑 康
(西南石油大学 土木工程与测绘学院,四川 成都 610500)
0 引言
近年来,风险感知受到学者的广泛关注。来自民航、采掘、能源、医药、交通等领域的研究均证实,风险感知会对安全行为产生重要影响,风险感知偏低的个体更可能实施不安全行为[1~6]。可见,深入研究风险感知偏差的形成与演化具有重要价值。
一般认为,风险感知包含对事件发生概率的感知和对后果严重程度的感知两个维度[7],而前者又被称为主观概率估计。主观概率估计是人们对不确定性事件发生可能性大小的估计,是人类推理和决策的基础[8]。目前相关研究主要集中于动机、能力和采样三个方面。动机方面,刘永芳等[9]通过实验发现,面对收益时,自我决策比预期他人决策表现出更强的风险偏好。Sharot[10]提出个体倾向于高估对自己有利事件的可能性,低估对自己不利事件的可能性。刘晓东和刘力臻[11]认为在预期效用值相近的情况下,避免后悔或追求欣喜成为影响决策的主要因素。Polman等[12]认为追求认知的一致性是导致认知偏差的重要原因。张萍等[13]采用实验方法证实了情绪一致性动机的影响。段婧等[14]通过实证研究证实了自我保护动机的存在。Pachur[15]等认为个体越倾向于使用补偿性认知策略,其概率估计越准确。Wang等[16]研究发现在从属动机会扭曲个体感知,使个体在判断中呈现出非理性的羊群特征。Raue[17]等和Sun等[18]均发现,在获益情境下,个体为远心理距离的人决策更冒险。陈庆等[19]通过实验发现,积极事件下自我决策的主观概率比为他人决策更低。能力方面,Hilbert[20]认为人脑信息处理系统会产生噪音,从而导致主观概率偏差。邱晓雯等[21]认为,时间压力下的主观概率估计更容易产生偏差。Schwartzstein[22]通过研究发现经济人的选择性注意特征使其持续忽略一些重要变量,最终导致偏差。卢安文和乔宇炳[23]通过主观概率确定概率权重函数,构建了基于损失承受能力的通信消费者决策模型,并印证了该模型的可靠性。Suter[24]等认为改变社会距离会诱发个体对“概率”维度和“结果”维度的认知整合(补偿性策略)或认知忽略(非补偿性策略),进而影响概率的估计。Pachur等[25]发现不善于表征和理解概率信息是主观概率偏差的重要原因。杜秀芳等[26]认为在时间压力下个体的认知加工受到限制,更有可能依靠直觉和经验做出决策。采样方面的研究则认为受环境结构的限制,个体难以从环境中采集到无偏的、有代表性的决策样本,即存在采样偏差[27]。在安全生产领域,个体死亡这种极端损失情境可能导致安全信息获取的总体样本出现不可逆的偏差,这可以认为是采样偏差的一种极端表现,被命名为“死亡悖论”。张羽等[28]通过分析78份施工事故调查报告后初步证实了“死亡悖论”的存在。而后,张羽等[29]进一步证实了“死亡悖论”会导致安全风险概率估计出现偏差。然而,为了实现安全冗余,现实中普遍存在组内平级互检或上级检查等措施。这些措施也可能对群体的概率估计产生影响。但针对此问题的研究文献尚未见到。
笔者拟将分组检查措施引入个体死亡条件下安全事故主观概率演化过程,建立元胞自动机模型并基于Netlogo平台进行仿真研究。为深化研究内容,本文先采用仿真图形对比方法得出初步结论,再通过重复交叉实验获取数据,并运用SPSS软件进行层次回归分析,以探究个体死亡条件下,不同分组方式对群体主观概率累积偏差的形成和演化规律,为安全心理和行为干预提供参考。
1 模型描述与构建
1.1 演化过程描述
现实中安全事故主观概率演化过程如图1所示。其中,组员对事故率的主观概率估计会影响其安全行为。在事件判断阶段,若组员未实施不安全行为,则进入下一轮循环;反之,组员不安全行为或被检查纠正并进入下一轮循环,或未被检查纠正则经历的事件数量累积一次,相应主观概率也随之更新,并进入事故判断阶段。在事故判断阶段,若不安全行为未导致事故发生,则进入下一循环;反之,则组员经历事故数量就累积一次,相应的主观概率也随之更新,并进入死亡判断阶段。死亡判断阶段,若事故未导致组员死亡,则进入下一轮循环;反之,则所在组织引入新员工替代死亡组员。由于整个过程涉及组员自身、组员间及组员群体间多层次演化关系,事故发生、组员死亡等多种状态及主观概率变化、组员补充等多种行为,属于复杂系统演化问题,故选择元胞自动机进行仿真。
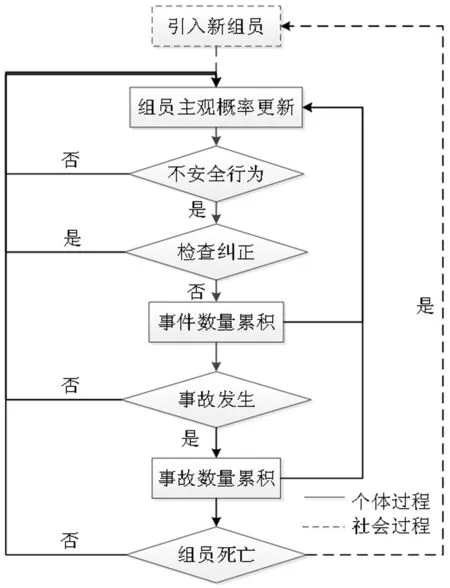
图1 主观概率演化过程
1.2 模型构建
元胞自动机(Cellular Automaton)是一类时间和空间都离散的动力系统。该系统由有限个元胞组成,某一时刻某一元胞的状态只与其自身及其邻居有关,但元胞间简单的交互行为可以演化出复杂的宏观结果。元胞自动机模型因具有使用方便与可视化程度高的优点而被广泛应用于各领域。元胞自动机模型主要由元胞状态、元胞空间、元胞邻域选择以及演变规则四部分组成。本研究将元胞自动机模型表示为CA=(L,Q,S,f)。其中,CA表示元胞自动机,L表示元胞空间,Q表示元胞状态集合,S表示元胞邻域,f则表示元胞状态转换规则,具体如下:
(1)元胞:模型中以人形元胞代表社会中独立个体,且假设社会中个体总量保持不变,个体死亡后能在下一时刻及时补充。
(2)元胞空间:元胞空间是长宽均为41格、总计1681格的正方形栅格无界空间。
元胞状态:包含事件累计数量、事故累计数量、分组合作人数、主观概率值。主观概率值(Acciper,A)反映了社会中个体对事故发生概率的主观概率估计,其值大小决定元胞颜色深浅,主观概率值越大则元胞颜色越浅。个体的累积事件数量(Event-num,EN)和累积事故数量(Accident-num,AN )则分别表示从仿真开始到当前时点个体所经历的事件和事故的累积数量。分组人数(Combinations-num,CN)表示群体内分组方式,取值为1表示单人一组;取值为2表示双人一组;以此类推。同组成员只要有一人不发生失误则该组事故不会发生。
(3)转换规则:个体对事故率的主观概率估计规则如下:
①事件数量累积规则:
(1)

②事故数量累积规则:
(2)
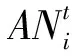
③主观概率更新规则:
(3)
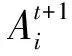
④分组事故概率规则:
pj=pCN
(4)
式中:p为一个人失误时所导致事故的客观概率,pj表示为第j组的客观事故率,CN表示该组的人数。整个公式表明,小组客观事故率受分组人数的影响,是分组人数的指数函数。分组人数越多,则该组事故发生的累积概率越小。
2 仿真实验分析
2.1 仿真实验过程
根据以上模型设定,确定本实验自变量包括事故率、死亡率、事件率、时间、初始人数、分组人数、替代元胞;因变量包括主观概率平均值(Mean)及其离散系数(CV)。据此运用Netlogo软件构建仿真实验平台。
各变量名称、含义及其取值范围如表1所示。经测算,单人遇到事故并死亡的概率为0.0021%,等于事故率乘以单次事故死亡率,根据海因里希法则将事故率设定为0.007,死亡率设为0.003;将程序运行时间设定为600步,初始人数为100;将事件率设定为1,以确保主观概率演化的有效性;分组人数设定为1,替代元胞开关暂不打开。根据变量取值进行仿真实验,具体步骤如下:
(1)将变量事故率的数值分别设置为0.007、0.02、0.05、0.2、0.5,初始人数设置为100,其余变量按初始值执行,得到此条件下的主观概率均值演化图2。
(2)将变量死亡率分别设置为0.003、0.8,初始人数分别设置为100、1000,其余变量按初始值执行,得到此条件下的离散系数演化图3。
(3)将时间设定为50步,分组人数设为1,初始人数设定为1000,替代元胞设定为1。将死亡率设定为0,事故率从0开始,以0.1为增量增加至1,但由于事故率为0时主观概率离散系数无法得出,故第一个值取0.01,从而获得11组数据样本;而后将死亡率设定为0.1,重复上述步骤,再获得11组数据样本;依此类推,死亡率以0.1为增量增加至1,但由于死亡率为1时主观概率离散系数无法得出,故最后一个值取0.99,共获取11×11合计121组数据样本。
(4)分组人数分别设为2、4,其余初始值不变,重复步骤3,再获得242组数据。
(5)将时间设定为600步,其余初始值不变,重复步骤3、4,再获得363组数据样本。
经过以上步骤,总共获得726组数据。

表1 研究变量描述
2.2 图形结果分析
由图2可知,主观概率均值演化过程均为先激增、后波动,最终趋于稳定,且近似等于客观事故率。说明随着经验的积累,主观概率估计偏差会逐渐减少,最终收敛于客观概率。由图3可知,离散系数随着时间的增长,先快速下降,后缓慢下降,最终趋于稳定。说明经验的积累可以减少群体内部主观概率估计的差异,且早期经验尤其关键。同时,当死亡率较高时,初始人数增加,离散系数的波动明显趋于平缓,表明群体总人数增加有助于平抑群体内部主观概率差异的波动、让群体主观概率估计更为一致。但死亡率较低时此现象不明显。
2.3 数值结果分析
由步骤3、步骤4和步骤5共得到程序数据样本726组。通过散点图分析,发现样本中存在26个离群值,参考文献[30]对这些离群值进行均值替换。而后,运用SPSS软件进行层次回归分析,先考察解释变量的主效应,而后加入事故率与死亡率交互项,检验是否存在交互效应。层次回归分析结果汇总如表2所示。其中,主观概率均值(50)和主观概率均值(600)分别对应程序运行50步和600步时的主观概率均值;主观概率离散系数(50)和主观概率离散系数(600)分别对应程序运行50步和600步时的主观概率离散系数。
由表2可知,模型1、模型2分别能解释因变量65.9%、64.3%的方差,增加一个交互项后的模型3、模型4分别能解释76.1%、83.7%的方差,且四者均显著,表明这四个模型均可接受。模型1和模型2中,分组人数标准化回归系数β值分别为-0.262,-0.245,表明分组人数对事故主观概率均值产生显著负向影响。提高分组人数,会加强小组内部监督,从而减少事故发生,但同时也会导致群体对事故主观概率的减少。事故率β值分别为0.625、0.615,产生显著正向影响,客观事故率的增加会导致主观概率均值较大幅度增加;死亡率β值分别为-0.45、-0.456,表明死亡率对主观概率均值产生显著负向影响,个体死亡会导致群体的主观概率出现系统性偏差,整个群体倾向于低估事故概率,但回归系数绝对值与文献[29]相比有所降低,表明分组措施能够降低死亡率导致的低估概率偏差。模型3和模型4中事故率与死亡率交互项β值分别为-0.784和-1.08,表明事故率越高,死亡率对主观概率均值的负向影响越大,二者存在互补效应,且随着时间推移,效应逐渐增强,但回归系数绝对值与文献[29]相比有所降低,表明分组措施能够降低互补效应。

图2 主观概率均值(初始个体数=100)

图3 主观概率离散系数
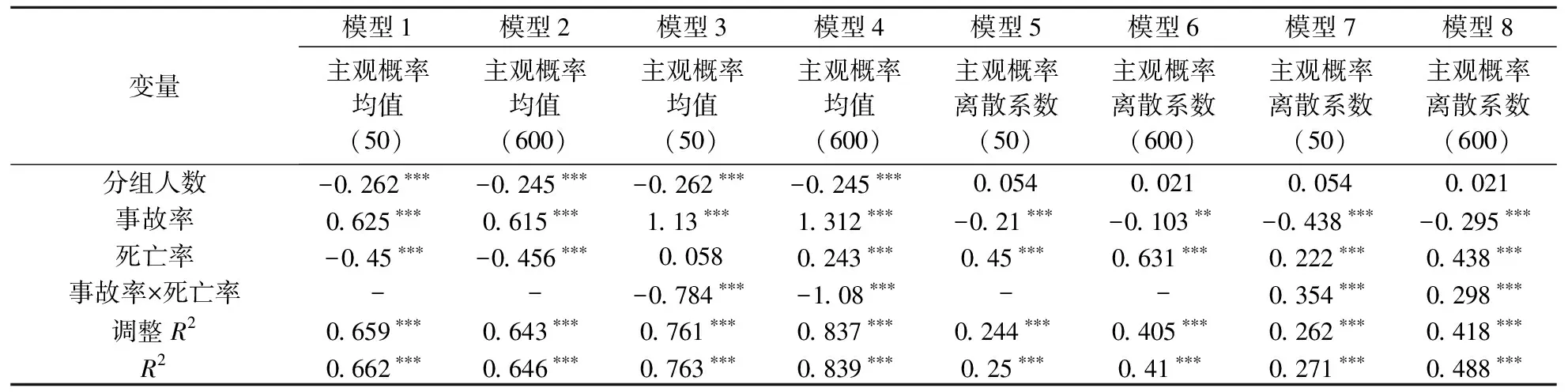
表2 层次回归分析结果汇总(因变量:主观概率均值、主观概率离散系数)

表3 事故基本信息
模型5、模型6分别能解释因变量24.4%、40.5%的方差,增加一个交互项后的模型7、模型8分别能解释26.2%、41.8%的方差,且均显著,表明四个模型均可接受。模型5和模型6中,事故率的β值分别为-0.21、-0.103,表明事故率的增加会缩小群体内部主观概率差异,但随着时间推移而减弱,表明客观事故概率的增大会减少群体内部主观概率的差异。与文献[29]相比该结果显著且稳定,回归系数绝对值也有所增加,表明分组措施能够强化事故率对群体内部主观概率差异的负向影响。死亡率的β值分别为0.45和0.631,表明死亡率对主观概率离散系数产生显著正向影响,死亡率的上升会大幅增加群体内部主观概率差异,但回归系数绝对值与文献[29]相比有所降低,表明分组措施能够降低死亡率导致的群体内部主观概率差异。模型7和模型8中,事故率与死亡率交互项β值分别为0.354、0.298,表明事故率越高,死亡率对群体内部主观概率差异的正向影响越大,二者存在互补效应,且随着时间推移,互补效应有所减弱。与文献[29]相比该结果显著且稳定,表明分组措施会强化互补效应。
经过共线性分析,8个模型的容差(Tolerance,TOL)、方差膨胀因子(Variance Inflation Factor,VIF)、特征值以及条件指数(Condition Index,CI)等指标均在可接受的范围内。但模型3、模型4存在中等共线性问题,导致其标准化回归系数β值大于1。
3 案例验证分析
为了验证上述结论,本文选取两个煤矿事故进行案例对比研究,事故基本信息如表3所示。其中,事故1为“吉林丰兴煤矿‘4.6’重大透水事故”,事故2为“安徽省淮南东方煤矿‘8.19’重大瓦斯爆炸事故”。两个案例的资料均来源于已公开的事故调查报告,二者同属于煤矿事故,具有一定可比性。对比两个案例可发现,在事故1中,由于现场第一目击者幸存,因此能够及时把事故信息传递出去,从而使得事故发生过程描述较为具体、详尽,包括临近事故发生时的行为、事故发生具体过程以及事后应急行为等,表明个体幸存有利于群体事故经验的积累;事故2中,事故发生过程描述几乎缺失,仅有外围目击者对爆炸烟尘的一句描述,对爆炸具体触发、演化情况无任何描述,表明个体死亡会对阻碍事故细节信息的获取,不利于群体事故经验积累。以上结论与仿真结果相符,验证了结论的合理性。对比两个事故发生原因可发现,其关键岗位上的工作人员普遍存在着未受过专业培训、不知道作业规程等现象。在事故2中,即便管理人员发现了事故预兆特征,但仍然心存侥幸,对事故发生概率产生低估,最终导致了事故发生。可见在高危行业中,事故主观概率存在群体性低估现象,这不仅验证了仿真结论的合理性,也凸显出低估主观概率后果的严重性。
4 结论
(1)群体主观概率演化一般会经历从急速变化到稳定的过程。建议对新成立或新员工较多的风险组织进行重点监管,通过引入有经验员工和经验分享使组织加速进入稳定期。
(2)增加分组人员数量有助于降低事故发生客观概率,但同时也会导致成员低估事故主观概率。群体组内成员通过彼此监督检查,能够提高安全冗余、减少事故发生的客观概率;同时,组内成员事故经验大幅减少,对事故概率的认知也停留在分组工作情况下,一旦改变分组方式,则成员的主客观事故概率差异将凸显出来,可能导致严重后果。建议对分组作业人员进行专项训练,提高其在不同条件下进行风险判断的能力。
(3)个体死亡会导致群体的主观概率出现系统性低估,且会加剧群体内部的主观概率差异,但分组措施能够降低以上偏差。显然,在死亡悖论视角下,高危行业事故主观概率往往更容易存在群体性偏差。建议注重组织安全文化建设,对高死亡率行业的组织安全文化偏差和差异进行重点监控。
(4)客观事故概率的减少会增大群体内部主观概率的差异,但分组措施能够降低以上差异。这意味着,群体成员对于小概率事故发生的可能性存在严重分歧,导致群体安全沟通困难和风险意识难以统一。
(5)事故率与死亡率存在互补效应,事故率的增加会强化死亡率影响,而分组措施一方面能降低其对主观概率均值的作用,另一方面会增强其对主观概率差异的作用。建议对易发生“小概率-极端损失”事故的行业进行专项安全认知动态监控和预警。
(6)群体总人数增加有助于减少主观概率偏差和差异,促使群体主观概率估计更客观、更统一。这表明群体规模对安全事故主观概率估计具有稳定作用。建议对涉及安全风险的小微企业进行重点监控。

