一种改进的多模式项目反应性调度问题

彭武良, 林家利

(烟台大学 经济管理学院,山东 烟台 264005)

0 引言

传统的资源受限项目调度问题(resource-constrained project scheduling problems, RCPSP)属于确定性项目调度问题，假定项目具有完全信息且项目的执行环境是静态不变的。也就是说，所有的项目参数在项目计划阶段均已知，而且这些参数在项目实际执行过程中不会发生变化。然而，这样的假定在现实中常常不成立，因为定义一个项目的所有参数在项目执行阶段都可能发生改变[1]。反应性调度又被称为重调度，指的是在项目执行过程中，发生干扰事件后，当基准调度方案变得不再可行或者不再最优时，对基准调度方案进行修改或者再优化的过程。根据是否考虑基准调度方案，可将项目反应性调度方法分为两类，一类是不考虑基准调度方案的完全重调度方法，完全重调度指的是按原调度问题的目标和求解方式对受到干扰的项目完全重新进行调度求解[2,3]。另一类就是考虑基准调度方案并以最大化基准调度方案的稳定性为目标的反应性调度方法。完全重调度与传统项目调度的调度方法和目标均相同，所以针对完全重调度的研究很少。既有的项目反应性调度问题主要是以最大化调度稳定性为目标的反应性调度问题。

反应性调度前后新旧调度方案的偏差越小则调度稳定性越高，且这种偏差通常用反应调度时产生的变更成本来衡量[4～6]。Van de Vonder等[7]、Deblaere等[8]、崔晓等[9]以最小化反应性调度前后活动开始时间的加权总偏差(即∑i∈Nwi·∣Si-si)为目标，其中，wi表示活动i的开始时间每提前或延迟一个单位所产生的成本，si为基准调度方案中活动i的开始时间，Si为新调度方案中活动i的开始时间。文献[4,5,10,11]均以最小化项目反应性调度成本为目标，但对反应性调度成本的定义不完全相同。其中，程序和吴澄[5]认为反应性调度成本应由活动时间变更费用、活动模式变更费用和项目拖期罚金三部分组成；张沙清等[4]将反应性调度前后活动开始时间的加权总偏差和项目拖期罚金两者之和作为反应性调度成本；Deblaere等[10]和王艳婷等[11]则认为反应性调度成本应由反应性调度前后活动开始时间的加权总偏差和执行模式转换成本组成。除上述目标函数以外，还有诸如最小化总体流程拖延、活动执行成本和计划修改次数的加权总和[12]、最小化项目工期与反应性调度前后各活动结束时间的加权总偏差之和[13]等比较小众的目标函数。在约束条件方面，绝大多数项目反应性调度问题模型[4,5,7,9,11,12]仅考虑紧前关系约束和资源约束，少数模型会在此基础上要求各活动的实际开始时间不能早于基准开始时间[8]，还有少数模型会将需要被重调度的活动的开始时间限制在恢复时间窗内[1]。

项目反应性调度问题从本质上可归类为RCPSP，是一种NP-hard问题。开发该问题的求解算法是项目反应性调度领域的一个重要研究方向。针对单模式的项目反应性调度问题，学者们已开发出一些精确算法[6]、启发式算法[7,8]以及智能优化算法[4]。Larsen和Pranzo[2]在既有研究的基础上构建了一个通用的反应性调度框架。除了上述单模式反应性调度问题以外，更为复杂的多模式项目反应性调度问题也引起了学者们的关注。Zhu等[1]为不确定性RCPSP提出了一种混合整数规划/约束规划的混合算法。程序和吴澄[5]、Deblaere等[10]分别设计了粒子群优化算法、几种精确算法和一种禁忌搜索启发式算法。Godinho和Branco[14]提出了不确定性下多模式项目调度的自适应模型，并设计出一种自适应调度策略。Chakrabortty等[13]针对抢占-重复模式下和抢占-恢复模式下的多模式反应性调度模型提出了一种反应性调度程序。为求解活动工期不确定情况下的多模式反应性调度问题，王艳婷等[11]设计了一种遗传禁忌混合搜索算法，崔晓等[9]则提出了一种双层禁忌搜索启发式算法。蒋淳等[15]针对项目型产品装配过程中的重调度问题，构建了以最小化项目成本和最小化计划变动偏差为目标的数学模型，并设计了基于帝国竞争机制的多目标算法。

虽然目前学者们对项目反应性调度问题的模型和算法进行了充分研究，但是，所有研究都聚焦于最小化反应性调度前后新旧调度方案的偏差。面对资源条件的不确定性，资源可用量增加时，项目进度在新的资源条件下原本可以加快，但既有的项目反应性调度方法无法满足项目管理者的该需求。总之，既有的项目反应性调度问题专注于最小化新旧调度方案的偏差，却无法保证新的调度方案在新的项目执行环境下是最优的。在更多的情况下，为了缩短工期、规避风险和提升项目绩效，保证新调度方案的最优性仍然是项目反应性调度需要优先考虑的问题。但是，既有文献中，尚无这方面的研究。

鉴于此，本文基于多模式资源受限项目调度问题(multi-mode RCPSP, MRCPSP)的框架，提出了一种改进的多模式项目反应性调度问题。该问题与既有研究不同，它首先保证新的调度方案在新的项目执行环境下是最优的，然后再最小化新旧项目调度方案之间的偏差。

1 问题描述与模型构建

1.1 问题描述

现假设：在项目执行过程中，资源可用量发生了改变而其他项目参数保持不变，并且，这样的变化在项目开始到项目完工这段时间内可能发生多次。资源可用量的变化很可能会使得原先制定的基准调度方案Πb变得不再最优甚至不再可行，这样的结果对于追求最短项目工期的项目管理者来说是无法接受的。此时，就需要进行反应性调度，在尽可能小地调整基准调度方案的同时，制定出能实现新环境下最短项目工期的新调度方案。然而，现有的反应性调度方法无法同时满足项目管理者的这两个需求。

因此，为突破现有反应性调度方法的局限，本文在现有多模式项目反应性调度模型(如崔晓等[9])的约束条件的基础上增加一个约束条件，要求新调度方案的项目工期等于新的资源可用量状况下的最短项目工期，以确保项目调度目标的最优实现，满足项目管理者“赶工期”的需求。

一般情况下，项目管理者都希望调整后的新调度方案和基准调度方案非常相似，因为新旧方案差异较大会引起人员、设备、物料等方面的大幅调整[16]，产生诸如必须更改与分包商的协议、累积库存成本、处理员工不满的不良后果[10]。所以，本文提出的多模式项目反应性调度问题以最小化反应性调度前后活动开始时间的总偏差与活动结束时间的总偏差两者之和为目标，以确保各活动的开始时间和执行模式都尽量保持不变。

总之，本文要解决的问题是：在项目执行阶段，资源可用量发生变化、其他项目参数保持不变的情况下，如何调整基准调度方案以获得一个新调度方案，该方案能够保证：(1)满足紧前关系约束和资源约束；(2)实现新的项目执行环境下的最短项目工期；(3)在此基础上，与基准调度方案之间的差异要尽可能小。其中(2)在目前的项目反应性调度研究中尚未受到关注。

1.2 模型构建

根据1.1节对问题的描述，本文提出的多模式项目反应性调度问题在尽可能缩短项目工期的前提下最大化调度稳定性，其数学模型如下所示:

(1)

(10)

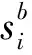
需要强调的是，与项目反应性调度的既有研究不同，本文在目标函数中同时最小化每个活动的开始时间偏差与结束时间偏差。这样既能保证各活动的开始时间尽量不变，还能要求新的调度方案尽可能不改变各活动的执行模式。另外，由于资源可用量在项目执行过程中可能变化多次，所以可能需要进行多次反应性调度。在本文中，每次反应性调度都以上一次反应性调度的结果为基础。也就是说，除了第一次调整以外，之后的每一次调整都将上一次调整后的调度方案定义为该次反应性调度的基准调度方案。

2 求解流程

针对问题特点，本文基于IBM ILOG优化编程语言OPL和CPLEX V12.8.0设计了该问题的求解程序，具体流程如下：

步骤1在项目计划阶段，假定所有项目参数提前可知且固定不变，制定一个满足紧前关系约束和资源约束的最优(即项目工期最短)调度方案作为基准调度方案Πb。

步骤2在项目执行阶段，资源可用量发生变化后，对新的资源条件下的项目进行完全重调度，得到新的资源可用量状况下可以实现的最短项目总工期δq。

步骤3由步骤2求得δq后，调用本文提出的改进多模式项目反应性调度问题模型，对基准调度方案Πb进行调整以获得新的调度方案Πq。Πq是新项目执行环境下所有实现最短项目工期的调度方案中，与基准调度方案Πb偏差最小(即活动开始时间总偏差与活动结束时间总偏差两者之和最小)的那一个。

步骤4若资源可用量再次发生变化，则先后执行步骤2、3，直至项目完工。需要注意的是，每次反应性调度都应该将上一次反应性调度后生成的新调度方案作为基准调度方案。

3 计算实验

3.1 实验设计

本节将对本文提出的改进多模式项目反应性调度问题、现有的反应性调度问题、完全重调度问题进行比较测试，三者的主要区别如表1所示。鉴于既有的反应性调度问题调度目标的多样性，为方便问题的比较，在本文的实验中，将现有的反应性项目调度问题的目标设定为“最小化反应性调度前后活动开始时间的总偏差与活动结束时间的总偏差两者之和”。

表1 三种不同类型的反应性调度问题的主要区别

在本文中，所有的调度问题均用IBM ILOG优化编程语言OPL建模，并用CPLEXV 12.8.0中的约束规划优化引擎(CP Optimizer)求解。运行配置为：Intel(R) Core(TM)i5-9500 CPU @ 3.00GHz (6 CPUs),～3.0GHz处理器；8192MB RAM内存；Windows 10操作系统。 从PSPLIB标准问题库的MRCPSP问题集中随机选取20个J20标准算例，J20中的每个算例包含20个实活动且每个实活动均有三种执行模式，涉及两种可更新资源R1、R2和两种不可更新资源N1、N2。设定两种不同的项目执行环境变化的情景：可更新资源R1、R2和不可更新资源N1、N2的可用量同时增加10%； R1、R2、N1、N2的可用量同时减少10%。随机选取各个算例的调整时刻q,q>0。

定义两个用于问题比较的优化性能评价指标：①COST，项目调度方案的变更成本，定义为反应性调度前后活动开始时间的总偏差与活动结束时间的总偏差两者之和；②MAKESPAN(简写为M-S)，反应性调度后新调度方案对应的项目总工期。

3.2 实验结果

情形1可更新资源R1、R2与不可更新资源N1、N2的可用量同时增加10%，其他项目参数保持不变。在该情形下，随机选取各个算例的调整时刻q，对随机选取的20个J20算例进行测试，得到三种不同的反应性调度问题的优化性能对比结果，如表2所示。其中，OM表示基准调度方案对应的项目总工期(即资源可用量变化前可以实现的最短项目工期)，FR表示完全重调度方法，NR表示本文提出的改进多模式项目反应性调度方法，OR表示现有的多模式项目反应性调度方法。

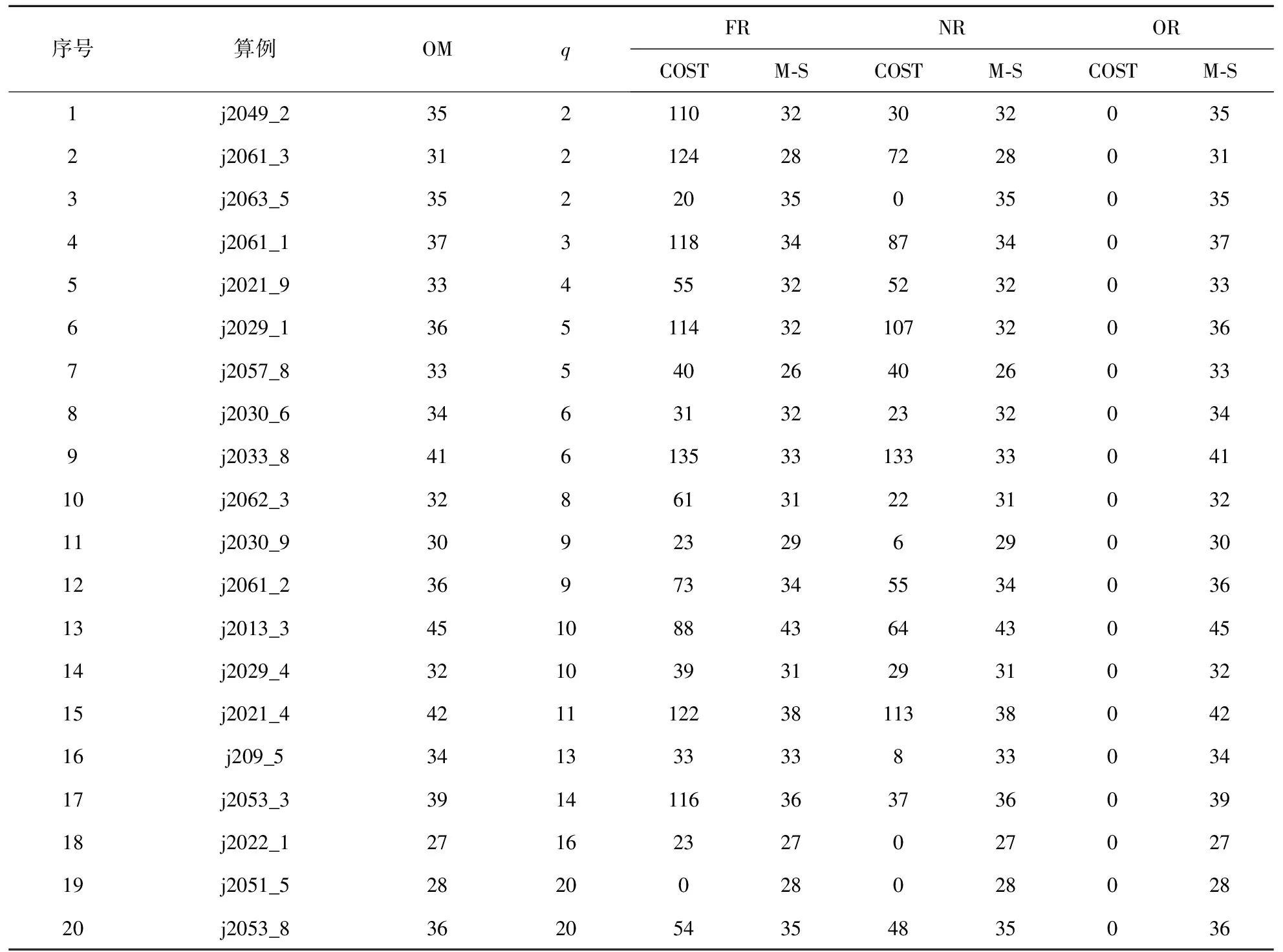
表2 资源可用量增加时三种反应性调度问题的优化性能对比结果

由表2可知，由于完全重调度的目标是最小化项目工期，所以完全重调度方案的项目工期在新的资源条件下在三种反应性调度方法中总是最短的。但由于完全重调度不考虑基准调度方案如何，所以完全重调度方案的变更成本在三种反应性调度方法中总是最高的。在资源可用量增加而其他项目参数保持不变的情况下，基准调度方案必定满足新的项目执行环境下的紧前关系约束和资源约束，即满足现有的多模式项目反应性调度问题的约束条件，再加上现有的反应性调度问题以最大化调度稳定性为目标，因此，最终的调度结果会是：不对基准调度方案做出任何调整(表现为OR的COST为零)。但是，像这样保护调度稳定性是有代价的，代价是放弃缩短原本可以进一步缩短的项目工期，所以，通过OR求得的新调度方案对应的项目工期是三种反应性调度方法中最长的。由表2还可知，对算例进行本文提出的改进多模式项目反应性调度，得到的新调度方案的项目工期总是与完全重调度方案的项目工期一样长，也就是说，这些新调度方案实现了新项目执行环境下的最短项目工期。与此同时，通过NR求得的调度方案的变更成本明显低于完全重调度方案的变更成本。所以说，本文提出的多模式项目反应性调度问题明显优于完全重调度问题。对于想要赶工期的项目管理者来说，与现有的项目反应性调度方法相比，本文提出的项目反应性调度方法显然更优。

情形2可更新资源R1、R2与不可更新资源N1、N2的可用量同时减少10%，其他项目参数保持不变。在该情形下，随机选取各个算例的调整时刻q，对随机选取的20个J20算例进行测试，得到三种不同的反应性调度问题的优化性能对比结果，如表3所示。

表3 资源可用量减少时三种反应性调度问题的优化性能对比结果

由表3可知，通过NR求得的调度方案的项目工期总是最短的，等于完全重调度方案的项目工期，而通过OR求得的调度方案的项目工期总是最长的。完全重调度方案的变更成本在三种反应性调度方案中最高，通过OR求得的调度方案的变更成本是最低的，而通过NR求得的调度方案介于两者之间。因此，本文提出的改进多模式项目反应性调度问题兼顾了调度稳定性的保护和项目调度目标(如最小化项目工期)的最优实现。

综合来看，本文提出的两阶段多模式资源受限项目反应性调度问题能够很好地应对项目执行过程中的不确定性因素，无论是在维护调度稳定性上还是在确保项目调度目标(如最小化项目工期)的实现上，均优于完全重调度问题。在确保项目调度目标的最优实现方面，与现有的项目反应性调度问题相比，本文提出的项目反应性调度问题具有明显优势。

4 结论

本文的主要贡献体现在两个方面：(1)对既有项目反应性调度问题的模型改进。本文提出的改进多模式项目反应性调度问题以最小化反应性调度前后活动开始时间的总偏差与活动结束时间的总偏差两者之和为目标，在既有反应性调度问题的紧前关系约束和资源约束的基础上增加了约束条件，确保反应性调度方案实现新的项目执行环境下的最短项目工期。(2)两阶段项目反应性调度方法的提出。在第一阶段，面对新的项目执行环境，对项目进行完全重调度，得到新的最优调度目标值；在第二阶段，以新的最优调度目标值为约束，以最大化调度稳定性为目标，求得新的最优调度方案。

基于标准算例，对本文提出的反应性调度方法、既有的反应性调度方法、完全重调度方法进行了充分的比较测试。测试结果表明，本文提出的反应性调度方法在缩短项目工期、保护基准方案的稳定性方面具有明显优势。未来可以尝试为本文提出的多模式项目反应性调度问题设计高效的启发式算法。