基于MIKE21FM的某城际铁路跨河桥阻水分析

董 慧，胡 超，王 克，张亚伟

(1. 北京闪通达技术有限公司 北京 100070；2. 北京禹冰水利勘测规划设计有限公司 北京 100161)

在跨河桥防洪评价工作中，阻水比作为分析工程建设项目对行洪影响的重要指标，一直是桥梁类防洪评价审查的重点[1]，在《北京市市属河道管理和保护范围内建设项目管理规定》《海委审批权限范围内涉河建设项目技术审查规定(试行)》等水行政主管部门下发的审查规定中均对阻水比进行了规定，要求新建、改建、扩建桥梁时桥墩阻水比不大于5%。根据以往经验，公路桥梁一般能满足阻水比不大于5%的要求，但由于铁路对振动幅度控制比公路、高铁要求更加严格，而桥墩越粗刚度越大振动却越小，因此，高铁桥墩相比公路桥墩更为粗大，导致通常无法满足5%的阻水比要求。

在桥梁工程阻水影响分析方面，国内已有关于桥梁阻水比方面的研究成果[2-4]，笔者认为对于复式断面河道或断面流速分布不均的河道采用阻水比指标分析行洪影响存在一定片面性。本文在分析桥墩阻水影响时引入了流速因素，提出了阻断流量比的概念和计算方法，并以某城际铁路跨河桥为工程实例，结合数学模型模拟的流场结果分别计算了桥梁阻水比、阻断流量比、壅水高度指标，进而分析了桥梁建设项目对河道行洪的影响程度，可为同类防洪评价项目提供参考。

1 工程概况

某河道干流全长144.54km，河身蜿蜒曲折，坡度平缓，平均纵坡1/10000，堤距变化较大达50～1500m，主槽宽50～80m，河床土质以壤土为主。河道地跨北京、河北和天津三省市，流域面积10288km2，其中山区为4353km2、平原地区为5935km2。根据相关规划，河道防洪标准为20年一遇，设计流量400～1300m3/s。铁路跨河处20年一遇设计流量469m3/s，河道为复式断面，纵坡1/25000，主槽宽约22m，堤距约为1032m，设计堤顶宽6m，堤防迎水坡和背水坡坡比均为1∶3，左右堤等级均为3级。

城际铁路跨河段桥梁全长1194.1m，自河道右岸至左岸，采用(40+64+40)m跨右堤+(60+100+ 60)m跨主槽+3×(48+80+48)m+(8×40)m+(40+ 64+40)m跨左堤。桥梁孔跨为8孔40m简支梁、3联(48+80+48)m连续梁、1联(60+100+60)m连续梁。桥梁采用连续梁一跨跨越主槽，滩地内共布设20座桥墩。桥墩采用圆端型桥墩，基础采用桩基础。

2 模型的构建

2.1 模型简介

MIKE21FM作为一款可以解决带自由表面的二维水流流动问题的通用数值模型，是专门为海洋、河口、海湾和内陆的河流、湖泊等区域相关课题的模型研究工作而开发的，包括水动力、波浪、泥沙和水质水生态等模块，其中水动力模块常用于模拟河流、湖泊、河口和海岸地区的水位变化和由于各种力的作用而产生的水流变化。

2.2 模型控制方程

平面二维水流运动控制方程如下：

连续性方程：

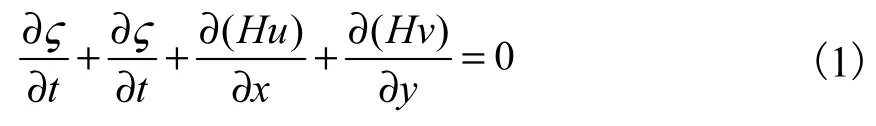
运动方程：

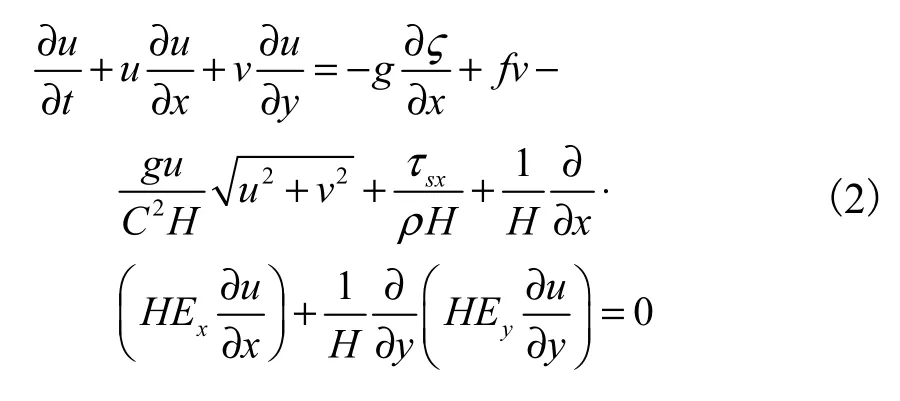
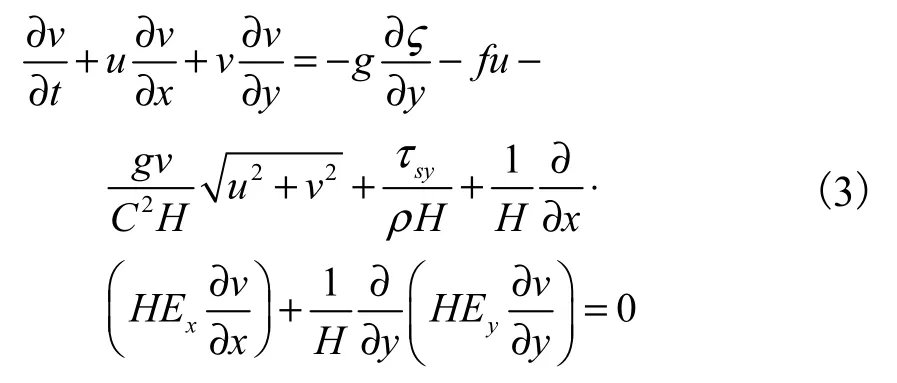
物质传输方程：

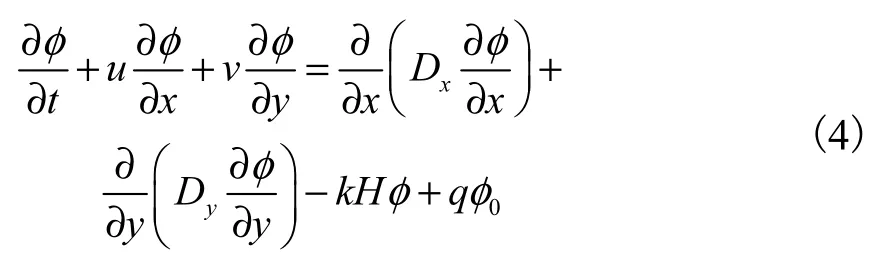
式中，ς为相对基准面水位，m；H为水深，m；t为时间，s；ρ为水的密度，kg/m3；g为重力加速度，m/s2；C为谢才系数，m1/2/s；f为柯氏力系数，s-1；τsx、τsy为风生应力；Ex、Ey为x、y方向广义的涡粘性系数，m2/s；u、v为x、y方向水深平均流速，m/s。

2.3 研究范围及网格剖分

数学模型计算范围为桥位上游6.70km，桥位下游5.70km，全长12.40km。

模型采用非结构性网格(三角形网格)进行网格划分，总网格数71458个，埝子堤内主槽部分剖分的三角形网格面积不大于168m2(单元边长设定为不大于15m)，两岸滩地内剖分的三角形网格面积不大于675m2(单元边长设定为不大于30m)。

2.4 模型计算参数

2.4.1 模型糙率

根据相关防洪规划和现场实地踏勘情况，主槽部分曼宁系数M取44.44(糙率n＝0.0225)，滩地部分M取14.286(糙率n＝0.07)。部分区域根据现场实际踏勘情况合理设定糙率值。

2.4.2 水平涡动粘滞系数

采用Smagorinsky公式计算水平涡粘系数，表达式如下：

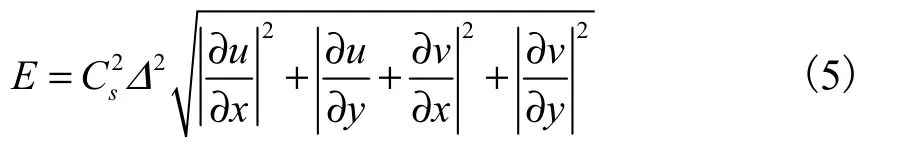
式中，u、v分别为x、y方向垂线平均流速，m/s；Δ为网格间距；Cs为计算参数，0.25＜Cs＜1.0。本次计算Cs取0.28。

2.5 边界条件

初始条件：采用稳定流计算，即模型试算稳定流场作为初始条件。

河道边界：固定壁面边界。

开边界：分别采用水位和流量控制。河道上游采用流量控制(469m3/s)，下游采用水位控制(4.69m)。

2.6 模拟结果

经过模型演算，得到建桥后桥梁跨越处20年一遇河道洪水位为4.76m，河道主流线位于主槽，主槽流速较大(集中在0.50～0.75m/s)，滩地流速偏小(集中在0.05～0.25m/s)。洪水流速分布见图1。

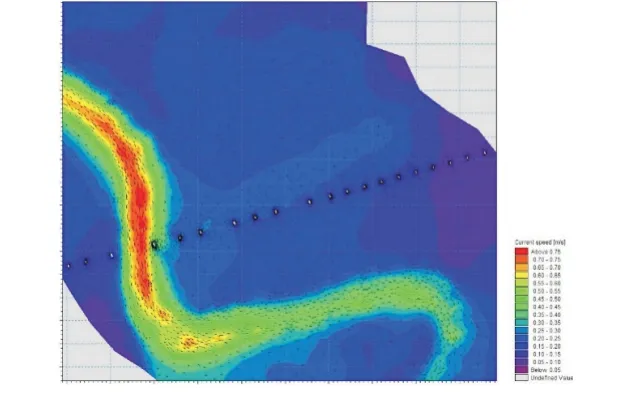
图1 建桥后流速分布图Fig.1 Flow velocity distribution diagram after bridge construction

3 阻水计算分析

基于MIKE21FM模拟结果，分别计算桥墩阻水比、阻断流量比、壅水高度。

3.1 阻水比

在桥梁工程的防洪评价中，桥墩阻水比一般指桥墩断面垂直于洪水流向的投影面积(f)与桥梁位置河道断面总面积(F)的比率，即阻水面积比，用来反映桥墩占用河道的情况和阻水程度。计算f首先要根据规范[5]计算桥墩阻水宽度B，见图2，公式如下：

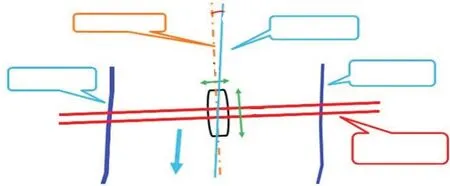
图2 桥墩阻水宽度计算示意图Fig.2 Schematic diagram of bridge pier water-blocking width calculation

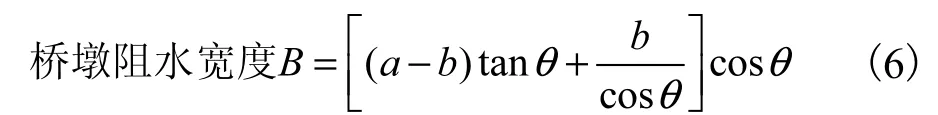
式中，a为桥墩长度，m；b为桥墩宽度，m；θ为桥墩轴线与河道水流方向的交角。

经计算，跨河桥桥墩阻水比(f/F)为8.10%。

3.2 阻断流量比

根据模型模拟结果，发现河道断面内流速分布不均，主流线位于主槽，主槽流速较大，滩地流速偏小，而主槽内未布设桥墩。因此，单纯计算阻水面积比结果并不能客观地反映桥墩阻水程度，有必要将流速因素考虑在内，并通过计算阻断流量比来进一步分析桥墩阻水影响。阻断流量比为桥墩断面阻断的流量(q)与桥梁位置河道断面总流量的比率(Q)。

根据模型计算结果，发现桥梁所在断面流速分布不均，应分别计算每个桥墩的阻断流量进行累加，再除以断面总流量得到阻断流量比，计算公式如下：

式中，q/Q为阻断流量比；n为桥墩数量；vi为第i个桥墩处的流速，m/s；hi为第i个桥墩处的水深，m；Bi为第i个桥墩的阻水宽度，m；Q为断面总流量，m3/s。

该桥梁在河道内共设置20个桥墩，统计每个桥墩位置处的流速、水深和阻水宽度，并分别计算各桥墩阻断流量和总阻水流量，见表1，再与河道断面总流量比较计算，最终得到该跨河桥桥墩阻断流量比(q/Q)为4.89%。

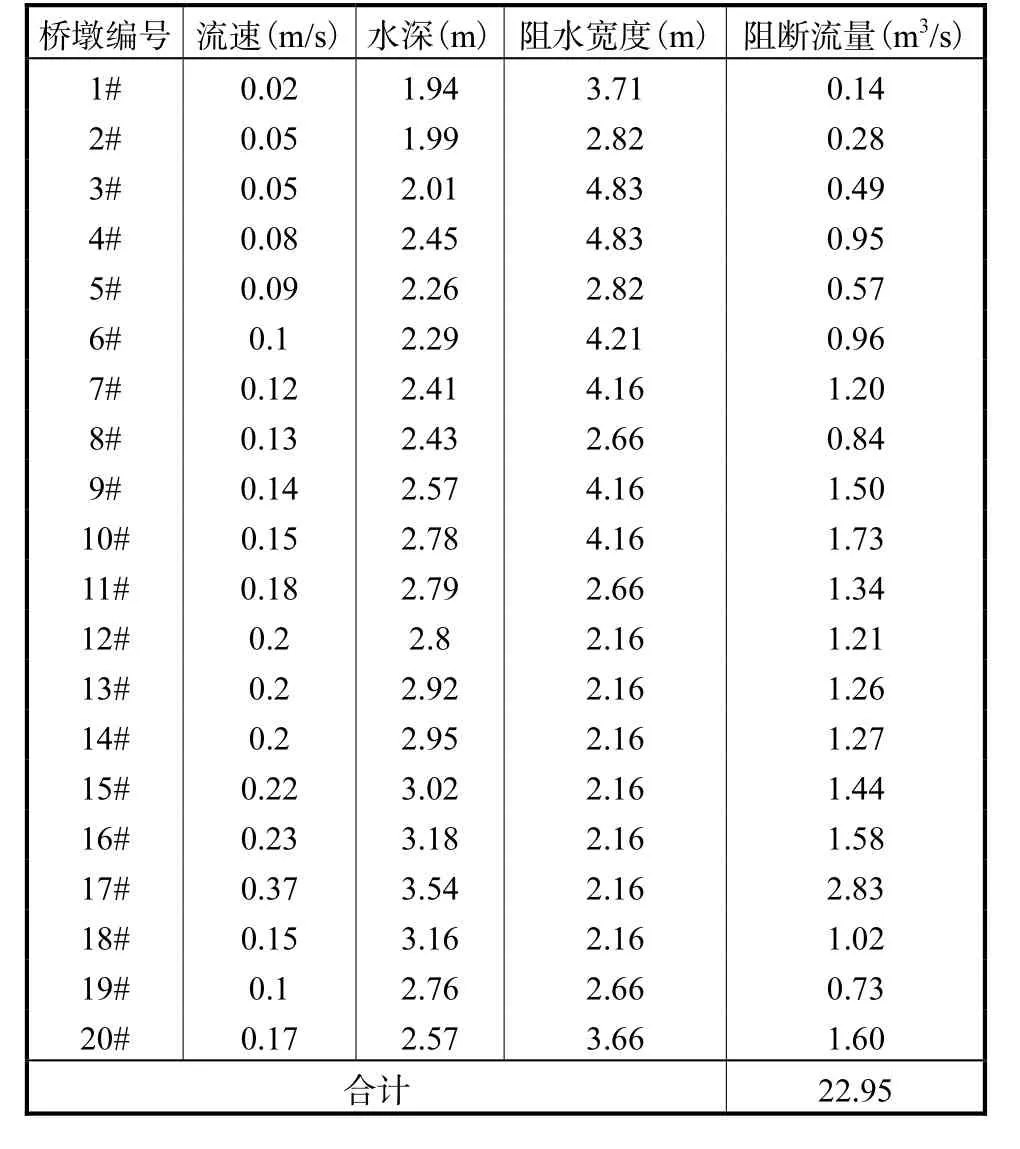
表1 桥墩阻断流量计算表Tab.1 Calculation table of bridge pier flow-blocking

3.3 壅水高度

桥前最大壅水高度按照下式计算：

式中，ΔZ为桥前最大壅水高度，m；η为系数，按规 范[5]取值0.10；为桥下平均流速，m/s；为断面平均流速，m/s。

同时，结合模型模拟结果得到建桥后壅水高度为0.017～0.022m。

3.4 结果分析

通过某城际铁路跨河桥实例分析，得到桥墩阻水比为8.10%，超过了水行政主管部门关于“新建、改建、扩建桥梁时桥墩阻水比不大于5%”的规定。按照以往的审查规定，该桥梁方案应不予通过审查。

但是通过对河道流场分布进一步分析，河道断面内流速分布不均，主流线位于主槽，主槽流速较大，滩地流速偏小。实例中的桥跨方案已经充分考虑了桥梁建设对河道主流线的影响，采用了一跨跨越主槽的方式布置，在主槽内未布设桥墩，一定程度上减小了桥墩阻水的影响。经计算，桥墩阻断流量比仅为4.89%，同时经过壅水分析，桥墩壅水高度仅为0.017～0.022m，壅水高度较小，进一步证实了桥梁建设对河道行洪没有明显不利影响。桥墩布置方案较为合理，水行政主管部门最终批准了该桥梁工程的建设。

综上所述，由于铁路桥墩粗大，阻水面积比往往会超过审查规定的要求，但对于具有主槽的复式断面河道，其断面内流速分布不均，防洪评价单位可根据二维水动力模拟结果给予桥梁建设单位合理建议，优化桥墩布设，避开高流速区域，优化后的桥墩阻断流量比一般可下降至理想数值，最终使得桥梁建设对河道行洪的影响控制在可接受范围内。

4 结 语

本文以某河道上跨河城际铁路桥为例，通过搭建水动力模型模拟了河道流场分布，分析了跨河桥桥墩阻水比、阻断流量比、壅水高度。结果表明：对于复式断面河道，应重点关注阻断流量比，阻断流量比把河道断面流速分布不均的因素考虑在内，更能客观反映桥墩建设对河道行洪的影响程度，进而弥补以往单纯计算阻水面积比的片面性。分析结果对优化桥墩布置方案具有重要的指导意义，可供同类防洪评价项目参考或借鉴。■