分类讨论思想在高中数学解题中的应用

◎陈明辉

(福建省莆田市仙游县私立第一中学，福建 莆田 351200)

一、引言

分类讨论思想在高中数学解题中的实际应用，更加偏重于对存在不确定性条件的题目进行求解，该思想方法能够充分激发学生的发散性思维，并促进其对数学概念和知识点进行深度理解分类讨论思想在数学解题中的应用需要根据题目中的关键内容进行变化，便于对专项内容求解高中数学学科的知识体系比较复杂，因此教师需要科学地引导学生运用分类讨论的数学思想

二、分类讨论思想的应用原则

(一)整体的完整性

知识分类能够有效地激发学生的关联记忆能力，并对高中数学的关键知识结构进行完善实现高层次的知识体系构建过程在应用分类讨论思想解题的过程中，我们需要考虑整体的完整性，对某个数学问题进行拆解的同时，还需要保障分类要素与整体之间的关联性在保证问题完整性的基础上，对数学问题的不同维度和量化分析过程进行模块化分析，并对分类讨论之后的分类各项内容进行有效整合，保障解题结果的完整性以解析几何问题为例，我们解题时需要将问题中的点线面作为关键的分类脉络信息，并对平面解析几何和空间立体解析几何问题中不同的侧重点进行详细分析，并在完成分类讨论之后，对解题过程进行整合整体的完整性是保障分类讨论过程实效性的基础要素，也是逐步拆解数学问题的主要方式根据整体的完整性，我们需要对分类讨论过程中的“整—分—整”解题思路进行深度解析

(二)分类各项的相斥性

我们在数学解题过程中，需要确定分类各项之间的相斥性，不能够存在交叉条件，熟悉这一过程能够有效提升学生的数学抽象思维能力分类各项存在的相斥性，与统计概率之间的互相独立原理基本相似，需要将不同控制条件与分类讨论结果进行有效关联，并将单一条件下的题目进行分类讨论针对在数学解题过程中分类各项之间存在的相斥性，我们需要引导和激发学生对分类讨论步骤和流程的完整性记忆能力，并强化学生的抽象逻辑思维能力根据相互独立的控制条件，学生可在解题过程中对分类各项存在的相斥性特征进行深度解析，并能够对不同独立分支的条件进行单独论述，充分保障解题过程的完整性和正确性分类各项之间的相斥性，也是构造分类讨论应用解析过程的关键因素之一

(三)分类层次的递进性

教师在讲述数学解题过程时应用分类讨论思想，还需要重点关注分类层次的递进性，并保障分类各项之间的独立性根据不同知识结构中的实际应用类问题，学生需要分析应用题型中的关键知识点，并合理运用分类讨论思想，对分类层次的递进性特征进行深度理解有些平面解析几何题目需要从多个角度分别探讨点线面之间存在的关系，因此，学生在分类讨论的过程中，需要对单一变量进行控制，并对其他两项条件进行分类讨论，虽然过程烦琐一些，但是能够充分体现各分类层次之间存在的递进性特征分类层次与学生的抽象逻辑思维能力直接关联，有些需要分类讨论的题目就是在考查学生是否具备应用某个知识体系的能力，因此对递进的分类层次进行详细探讨，有利于学生不断完善自身解决不同类别的实际应用问题的知识体系

三、分类讨论思想在高中数学解题中的有效应用

(一)三角函数求解问题

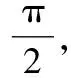
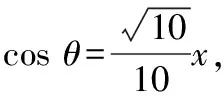
该题目需要利用分类讨论思想进行分析和解答，教师可以此为例，引导学生运用分类讨论思想分析三角函数求解问题

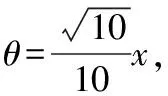
(二)数列分析问题

在高中数学学科的知识体系中，数列分析问题是分类讨论思想主要应用的题型之一，也是协助学生构建多维度数学知识网络的关键内容高中生需要对数列的基本概念、等差数列、等比数列以及数学归纳法等相关知识进行理解和应用，并对分类讨论思想的应用思路展开探讨以人教版必修教材为例，教师可以充分引导学生对实际应用类问题中的数列分布规律以及累加和、累积等题目进行自主探究式学习，并对分类思想的应用方法思路进行深度分析对于分析数列问题的不同实际应用场景，学生能够将相应的等差数列和等比数列的分类过程进行深度梳理，并对数列求和等相关实际问题进行分类讨论学生在应用分类讨论思想的过程中，可能会存在较多问题和障碍，此时高中数学教师需要将不同解题思路和思维模式的构建方式进行深度拆解，协助学生完善解题策略

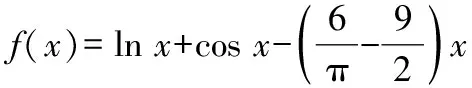
在该题目中，问题(1)相对简单，基本所有学生能够通过函数求导计算和基本的已知条件进行分析解答而问题(2)相对复杂，由于数列项数的奇偶性未知，且其奇偶性对表达式和表达式均有影响，需要学生进行分类讨论

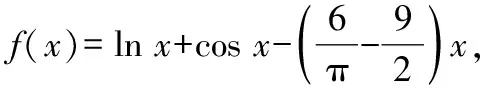
(三)曲线类型讨论问题

在高中数学学科的知识体系中，函数与方程是大多数学生学习的难点，曲线类型讨论问题是分类讨论思想在实际应用类问题中的主要内容很多学生对平面解析几何和空间立体几何类问题比较迷惑，以人教版必修教材为例，圆锥曲线方程需要将椭圆、双曲线以及抛物线作为主要解题思路在对曲线类型进行分类讨论的过程中，教师需要引导学生重点关注关键点坐标的位置变化规律，以及极值点在平面直角坐标系中的变动规律有些综合类题目会将空间几何体中的动点作为研究对象，并对动点不同的运动轨迹进行分类讨论，那么曲线类型的基本概念和关键点的位置坐标就是主要分类讨论的分类项，并对不同递进关系进行有效排序曲线类型分类讨论问题需要对变化项和不变项之间存在的线性与非线性关系进行深度解析，协助学生深度理解曲线类型讨论问题的解题策略

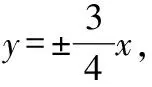
由于双曲线焦点位置不确定，既可能在轴上，又可能在轴上，因此其离心率数值也不确定，需要展开分类讨论

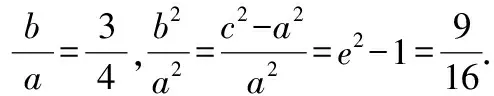
(四)函数极值问题

函数极值问题是高中数学学科知识体系中的重点内容之一，也是迷惑很多学生的难点内容函数极值问题不仅可以参考函数导数的计算方式，还可以利用数形结合的方式进行求解，并对分类项进行递进排序，教师可引导学生进行有效地分类讨论以人教版必修教材为例，很多学生在面对幂函数、指数函数、对数函数、三角函数等相关函数应用类问题时，思维模式很容易被固定住，因此教师需要引导学生合理运用分类讨论的解题思想，并对不同函数的极值分布情况进行分类讨论，对于具备较多隐含条件的函数极值问题进行分类求解，对所有分类项进行有效排序，保障分类过程的可视性和递进性函数极值问题的分类讨论方法，主要集中在函数图像的变换方法、极值坐标的分布规律以及变化规律等方面

已知函数()=-4+，(∈)(1)讨论函数的单调性(2)若函数在[-1,1]上的最大值为1，求实数的取值范围

在该题目中，无论是问题(1)还是问题(2)，都需要应用分类讨论思想尤其是问题(2)，函数极值已知，分析实数的取值范围，需要对的具体取值范围展开分类讨论下面重点对问题(2)的分类讨论展开分析

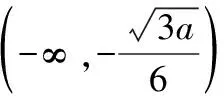
当=0时，≤1+4即0≤1，无论取任何值，条件均成立

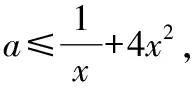
四、结束语

分类讨论思想是数学学科的重要思想理论体系之一，在高中数学学科的解题教学过程中，更加重视学生对分类讨论思想的解题策略的应用能力分类讨论思想在数学解题中的应用，需要根据题目中的内容进行变化，并针对专项训练内容进行变式求解根据相互独立条件，学生在数学解题过程中需要对分类各项存在的相斥性特征进行深度解析，并对不同独立分支条件进行单独论述