逆向思维在解析几何证明中的应用

◎陈锦玲

(广东茂名幼儿师范专科学校理学院，广东 茂名 525200)

一、逆向思维在解析几何证明中的应用

(一)分析法

当命题的条件比较隐晦，难以直接找到解题思路时，我们可以从问题的结论入手，往回思索，从求解问题追索已知条件，寻找解题的突破口

1设和′分别是坐标原点到点(,,)和点′(′,′,′)的距离，证明当′++′=′时，直线′通过坐标原点

即，，′三点共线，从而直线′通过坐标原点

这道题可以利用直线和平面位置关系的判定定理来做，先求直线的方向向量，再求方向向量和平面的法向量的向量积，另外在直线上取一点，判断它是否在平面上，这样做相对麻烦一点我们可以换一种思路，考虑到平面的方程是由直线的两个方程相加得到的，所以我们只需要证明直线上的任意点都在平面上，就可以确定直线在平面上了

显然有(++)+(++)=0，即点在平面上，由的任意性得直线在平面上

3用向量法证明平行四边形对角线互相平分

这道题看起来很简单，但课堂上笔者让学生做时发现，大部分学生都不知从何处入手：或是用命题本身来证明，或是通过“+=+”得到“=,=”,这显然是不符合逻辑的如果采用逆向思维，只要证明其中一条对角线的中点也是另外一条对角线的中点，这样它们就互相平分了，证明就显得轻而易举了证法如下：

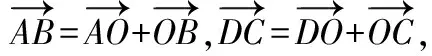
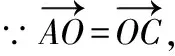
这两个证法独辟蹊径，达到了出奇制胜的目的受这新颖的想法和奇特的论证的影响，学生的大脑会受到鲜活的刺激而处于异常兴奋、活跃的状态，产生一种豁然开朗的感觉，从而对逆向思维产生深刻印象，对使用逆向思维解题产生浓厚兴趣

(二)反例法

为了让学生准确地把握某个命题的结论所成立的条件和范围,笔者在教学中常常构造一些反例, 用以纠正学生对某些概念的错误认知, 有利于学生从反面记忆定理、性质、法则，进而加深对知识的理解

4,,是非零向量，证明：若=，则有·=·,×=×，反之不真,即两向量数量积和向量积的消去律都不成立

数的乘法和加法都满足消去律在学习向量的运算时, 部分学生往往会受到数的乘法满足消去律的影响, 理所当然地认为向量的数量积和向量积也满足消去律我们要证明消去律不存在，只需要举一反例说明即可

如图1给出的三个非零向量,,，

因为·=||乘在上的射影，

·=||乘在上的射影，

又在上的射影=在上的射影，

所以·=·，

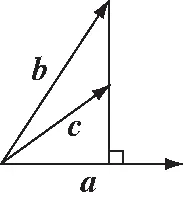
图1

但显然≠.

如图2所示，三向量,,中，因为与构成的平行四边形面积等于与构成的平行四边形面积(均等于||)，×与,都垂直,×与，都垂直，而且{,,×}与{,,×}同为右旋向量组，所以×=×，而显然≠.

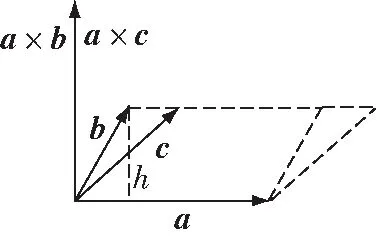
图2

5证明：经过双曲抛物面一条直母线的每个平面不一定经过属于另一族直母线中的一条

在族直母线中取一条直线(=1)为

因为≠0,所以直线不在平面π上，故过族直母线的平面π不经过族直母线中的任意一条

通过具体形象的举反例，不仅问题得以解决，而且使学生加深了对双曲抛物面的直母线的性质的理解，同时训练了学生的逆向思维，可谓一举三得

(三)反证法

反证法是从否定结论开始进行推理，直到推理出与已知条件或事实矛盾的结论，从而肯定原结论正确的证明方法由于此法将结论否定后作为条件加以利用，因此增加了推理过程中的前提条件，对于那些已知条件较少的问题，运用此法往往会达到意想不到的效果

6，，，是四个共面的向量，且,不共线，如果=,=，证明：=.

假设≠，即-≠,

由=，=得(-)=0，(-)=0,

即(-)⊥，(-)⊥，又，,，是四个共面的向量,

所以-,，共面, 因此得∥,这与题设矛盾, 所以=.

该题的证法不止一种，教师应启发学生从不同角度、不同方向思考问题，锻炼其逆向思维

(四)逆用命题结论

7利用向量法证明四面体对边中点的连线交于一点且互相平分

从命题的结论出发，只要证明“三组对边中点连线的中点是同一点”，就证明了“对边中点的连线交于一点且互相平分

设四面体-的一组对边，的中点分别为，，的连线的中点为，其余两组对边中点连线的中点分别为,，下证，，重合

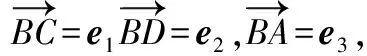
8证明三角形三中线共点

该题可逆用问题结论，利用三角形重心的性质来证明，即分别在三条中线上取到顶点的距离是它到对边距离的两倍的点，证明这样的三点重合

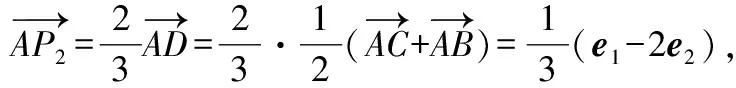
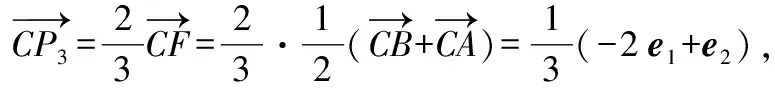
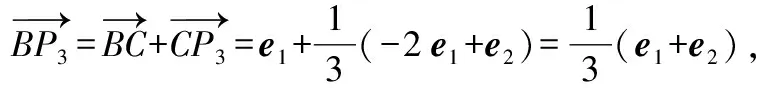
所以，，三点重合，

即三角形三中线共点

当命题的条件过于简单，从条件无从下手时，逆用命题的结论可使命题简化，解题思路清晰、独特，证法简捷明了

(五) “正难则反”原则

解决问题一般先从正面入手进行思考，但有些问题按这种方式会比较困难，甚至无从下手此时应调整思维方向，采取“顺繁则逆、正难则反”的思维策略，这样常会“山重水复疑无路，柳暗花明又一村”

9证明方程8+5+5+4+4-8-18+18-99=0表示的曲面是柱面

证明方程表示的曲面是柱面的常用方法，是把方程分解成一次因式的乘积，构造出直线族方程，证明这一族直线是平行直线，从而证明曲面是柱面但是这种方法在本题这里行不通，我们可采用逆向思维构造出一柱面，使它的准线是曲面与坐标面的交线，母线方向为∶∶，再求出这个柱面的方程，将这个柱面方程与原方程比较以确定∶∶，使两方程一致，这样就证明了原方程表示的曲面是一个柱面

母线方向为∶∶建立柱面的方程

在准线上任取一点(,,0)，那么过这一点的母线方程为

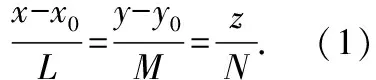
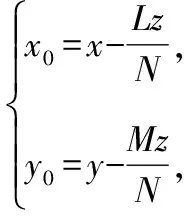
这种解法打破了常规，能够引导学生从多角度、多方位考虑问题，锻炼其逆向思维

二、结束语

在解析几何教学中，教师对学生除了进行常规的正向思维的培养外，还应有意识地加强逆向思维的培养，通过融会贯通正反两个互逆的思维过程，让学生摆脱由单一地正向思考导致的机械的、呆板的定式思维的束缚，打破单一的、僵硬的推理模式，帮助学生养成从不同角度分析问题、解决问题的习惯，培养其思维的敏捷性，提高其数学能力，从而达成让学生灵活掌握解析几何知识的目的