小学数学解题中转化思维的有效应用分析

◎吴云泽

(甘肃省平凉市庄浪县朱店学区，甘肃 平凉 746607)

一、引言

近年来，随着新课程改革的不断推进，新课标对小学数学教学提出如下要求：要让学生习得适应未来社会生活与继续学习所必需的数学基本知识及数学思想方法大量教学实践证明，培养学生使用转化思维解答数学问题的意识与能力，是培养学生数学核心素养的必要环节，与学生终身的成长和发展息息相关，因此，在课堂教学的过程中，教师应关注类似的问题，将转化思维不动声色地渗透数学教学的方方面面，促进学生的进步和发展

二、小学数学解题中转化思维的有效应用

(一)转化思维在计算题中的应用

计算能力是数学学科核心素养的重要组成部分，因此，在数学解决问题的教学中，教师要重视并引导学生形成使用转化思维解决计算题的意识与习惯，借助相应的计算题，增强学生对相关概念、公式的掌握，进而逐步培养学生计算思维的灵巧性，为学生使用转化思维解答计算题打下坚实的基础

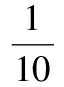
(二)转化思维在几何题中的应用

数学学科有着明显的抽象性、逻辑性与严谨性，这些特征在几何类知识、题目中有极为鲜明的体现，因此，学生普遍表示对几何类知识、题目存在学习、解题上的困难与成年人相比，学生的抽象思维较为薄弱，在学习知识、认识事物时，他们习惯使用形象思维，这更为他们解答几何题增加了不少的难度为降低学生解答几何题的难度，教师在平时应加强对学生转化思维的培养，如在教学几何类知识点时，教师可以借助多媒体设备，通过直观、形象的图片让学生更好地感受图形的变化特征，将新学的几何知识转化为已学的几何知识进行教学，这样不仅能在一定程度上提高学生的迁移能力，而且能增强学生的转化意识

以“组合图形的面积”一课的教学为例，该课内容较为抽象、复杂，学生学习起来有着较大的难度，如果未形成转化思维，那么很多学生都会遇到学习上的困难因此，教师可以在课堂教学的过程中，潜移默化、不失时机地为学生引入转化思维，使学生掌握使用技巧，帮助学生解决在学习过程中遇到的重、难点知识又如，在教学“多边形的面积”一课时，教师同样可以使用转化思维，帮助学生解决在学习过程中遇到的重、难点知识教师可以为学生出示如下例题(如图1)：求阴影部分面积教师可以引导学生结合数形结合思想、转化思想，列出如下解题思路：

图1

(1)设定这两个正方形的边长分别为与，梯形的面积可表示为(+)×÷2，三角形的面积可表示为(+)×÷2，两者面积相等；(2)三角形的面积=梯形的面积-梯形的面积，而三角形的面积=三角形的面积-梯形的面积，由此可推导得出三角形的面积=三角形的面积，最终可推导得出阴影部分的面积为÷2

这是一道典型的可使用转化思维来解答的习题在引导学生解答几何类习题的过程中，教师应多为学生渗透这种转化思维，让学生逐渐熟悉转化思维，使转化思维真正成为学生解题习惯的一部分

(三)转化思维在植树问题中的应用

“植树问题”在小学数学习题中，属于常见题型在培养学生的转化思维的过程中，教师可以多使用此类题目通常情况下，在以往的数学学习中，对于“植树问题”，教师大都引导学生使用化归方法来解答该类问题具体包括三种题型：一是两端都栽，此种情况下，棵数=间隔数+1；二是只栽一端，此种情况下，棵数=间隔数；三是两端不栽，此种情况下，棵数=间隔数-1在解答此类相关问题的过程中，学生会在脑海中形成一个相对固定的解题流程，即判断题目类型—选用公式—判断“树”与“间隔”—解决问题然而，学生在解题过程中还是会遇到较多的困难，如有的学生无法判断问题中求解的是树还是间隔，进而无法准确判断出该使用哪种公式解答问题；有的学生在判断题型、选用解题方法的过程中，会受到思维定式的影响，进而难以找到解答问题的切入点对于此类问题，教师皆应将教学重点放在辨别“树”与“间隔”上，尽可能地帮助学生厘清解题思路，此时，教师引导学生使用转化思维，能够取得较为良好的效果

教师可以使用如下教学方法来完成培养学生转化思维的流程：教师可以提问学生解答植树问题的心得，让学生分析几种植树问题之间的相同点与不同点，为转化思维的引入创造条件学生在探究的过程中会逐渐发现，“树”是始终比“间隔”多1 的，且“树”与“间隔”之间的关系并不是绝对的，有着相互依存的关系，这种关系是可以有效转化的在得出如上结论后，学生会对转化思维产生更为清晰、明确的认知在这之后，教师可以为学生出示解决“树=间隔数+1”“间隔数=树-1”的解题思路，让学生感受到这就是转化思维的典例，将学生的解题思维转变为判断题目求的是间隔还是树，使学生养成解决此类问题的正确习惯，这非常有助于促进学生数学核心素养的发展

在练习环节，教师可以为学生出示这道题：“在学校的一条大路上，共插有20面彩旗，若需在每两面旗帜中放一盆植物，需要放置多少盆植物？若想要每两盆植物中有一面旗帜，需要放置多少盆植物？”如果以传统思路解答这一问题，那么学生需要先判断题目的类型，判断出“树”与“间隔”，再形成解决问题的正确思路在确定应使用“树=间隔数+1”的公式后，学生会得到答案为19由于这一解题过程相对烦琐，学生需要经历复杂的步骤，才能得出答案然而，如果教师引导学生使用转化思维，就能帮助他们更为快捷地解答这道题目，学生也就可以直接判断题目中的“彩旗”是“树”，盆栽是“间隔”，之后确定“树”比“间隔”多1，如此高效解题在求解后一问时，如果学生采用传统思路作答，就会耗费较多的时间，此时，如果教师引导学生使用转化思维，就能帮助他们在两步之内得出答案是21，这体现了转化思维的实用性

三、培养学生转化思维的方法

(一)挖掘教材中隐藏的转化思维

毋庸置疑，数学思想并非独立存在，它依附于数学知识之上，体现在数学教材的方方面面目前看来，小学数学教材在编排上有着明显的规律性，在培养学生的数学核心素养方面，一是体现了对数学知识的传授，二是体现了对学生的数学能力、数学思想的培养为增强学生对转化思维的掌握程度，教师在平时应多挖掘教材中隐藏的转化思维，提高学生利用转化思维解决数学问题的能力，促进学生的进步和发展通常情况下，小学数学知识点分为四大领域，即数与代数、空间与图形、统计与概率、实践与综合，这四大领域皆体现着转化思想因此，在平时，教师应多挖掘教材中知识点之间的内在联系，让教材中隐含的这一数学思想成为学生学习数学知识、解决数学问题的基本方法，将转化思维真正内化到学生的能力体系之中，将其作用最大化发挥，增强学生的问题解决能力

(二)在新课传授中渗透转化思维

正所谓“授人以鱼不如授人以渔”在新课教学的过程中，教师应在为学生传授新知的同时重视为学生渗透相应的数学思想、数学方法，在数学知识与数学应用能力之间搭建一座桥梁，使转化思想真正内化到学生的脑海中在新课教学环节，教师应对数学元素做好因果分析，找到知识点之间的本质联系，之后引导学生将新知转化为旧知、将数字转化为图形，逐步培养学生的转化思维

1将新知转化为旧知

在数学知识体系中，各知识点之间有着极为明确的联系在新课教学的过程中，教师应培养学生对知识点之间联系的敏锐度，让学生认识到每个新知都是在已有的知识点之上建构而成的，进而为学生转化思维的形成打下良好的基础在实际教学中，教师常会引导学生在遇到陌生问题时，将陌生问题转化为他们熟悉的问题，并鼓励学生利用已有的知识点，解决新知学习中产生的问题，这其实就是转化思维的一种体现，能够帮助学生更好地掌握新知例如，在教学“圆柱与表面积”这一内容时，教师可以指导学生将圆柱的表面积转化为一个长方形(或正方形)和两个圆来计算在学生动手探究的过程中，教师可以先重点引导学生理解“转化后的一个长方形(或正方形)和两个圆是圆柱的哪一部分”，再引导学生讲讲为什么要将圆柱转变为一个长方形(或正方形)和两个圆来计算，将旧知“长方形的面积计算”“圆的面积计算”作为落脚点，找到新知识的建构点，在完成新知教学的过程中潜移默化地培养学生的转化思维再如，在教学“平行四边形的面积”这一内容时，教师可以将旧知“长方形的面积”作为新知识的建构点又如，在教学“三角形与梯形的面积”这一内容时，教师可以将旧知“平行四边形的面积”作为新知识的建构点，以此类推在如上教学手段的作用下，“转化思想”会逐渐深入学生的心中，成为学生解答数学问题的好伙伴

2将数字转化为图形

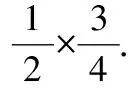
(三)在课堂总结中提炼转化思维

新课程改革高度肯定“教师是课堂的组织者、引导者与参与者，学生是课堂的主体”的教学理念，认为在教学过程中，教师要多与学生互动，在课堂中应给予学生充足的时间和空间来讨论数学知识，锻炼学生更好地总结数学知识内容，使各类数学思维真正内化到学生的脑海中从这一角度上看，课堂总结环节无疑是为学生渗透转化思维的关键环节教师做好这一环节的教学，有利于让学生完整地经历片面知识过渡到全面知识的全过程一般情况下，同一数学内容可表现出多种不同的数学思想、方法同理，同一数学思想、方法可以通过各种不同的内容展示出来，因此，在课堂总结环节，教师应把控好为学生渗透转化思维的时机，尽可能地让学生从数学思想的高度出发，把控知识点的本质，找到隐藏在知识点背后的内在规律例如，教师可以为学生出示这道题：“一个底面直径是20 cm，装有一部分水的圆柱形容器，水中放有一直径是12 cm、高是10 cm的圆锥体铅锤，该铅锤全部淹没于水中在将该铅锤从水中取出后，容器内的水会下降几厘米？”教师应要求学生认真审题，之后组织学生进行动手操作，并让学生在小组内部讨论具体的操作情况在学生讨论后，教师可以引导学生讲讲自己小组总结出的结论然后，教师进行总结这样一来，学生会切实感到转化思维有着十分突出的实用性，进而形成使用转化思维解决数学问题的意识，有助于自身数学核心素养的成长

四、结语

综上所述，在小学数学学习、解题中，“转化思维”不失为一种十分高效、实用的思维方法教师在平时应多结合具体的数学知识、数学题目，为学生渗透这一思维方法，培养学生使用转化思维进行高效解题的意识与能力，促进学生数学核心素养及综合素质的均衡发展