峰值电流控制模式SPWM-H逆变器斜坡补偿设计

薛天山，王玲桃

(山西大学 电力工程系，山西 太原 030013)

0 引 言

对于变换器的非线性动力学行为的抑制研究，一直主要集中在DC/DC变换器[1-2]，其他类型的电路涉及较少。单相H桥逆变器作为一种被广泛使用的电路形式，在新能源发电并网和微电网一系列的电力系统的应用中有很重要的意义。H桥峰值电流型控制电路比较简单，系统的动态响应较快，对电路有一定的保护作用，易于实现限流，因此峰值电流型控制方式在电力系统中得到了广泛的应用，但是这种控制方式在占空比较大，出现扰动时，电流的扰动误差会出现一直增大的现象，最终使系统失控。在很多非线性动力学行为的抑制措施中，斜坡补偿作为一种简单有效的方法[3]，得到了广泛的研究，可以通过建立一种逆变器的离散数学模型[4]，推导出斜坡补偿理论依据。本文研究了在电流模式下的单相H桥逆变器的工作原理以及非线性行为，介绍了斜波控制的原理，通过雅可比矩阵法建立离散数学模型，给出了斜坡补偿的理论依据，通过仿真加入斜坡补偿，仿真结果和数值分析结果一致，为单相双闭环峰值电流H桥逆变器斜坡补偿提供了一种理论设计依据。

1 峰值电流型SPWM-H逆变器工作原理

图1为双闭环峰值电流H桥逆变器原理图，电路由直流电源、开关Q1～Q4、电感L、电容C、电阻R以及RS触发器构成。参考电流为交流量时，变换器处于逆变工作状态。第一个周期，信号器发出时钟脉冲时，RS触发器发出高电平信号，开关Q1和Q3打开，Q2和Q4保持关闭，输出电流近似直线上升，变换器处于工作状态1。输出电流达到参考电流触发器复位，Q2和Q4打开，Q1和Q3关闭，电流开始下降，变换器处于工作状态2。下一个周期开始，下一个脉冲发出，触发器发出高电平，电流再次上升，变换器又回到状态1。

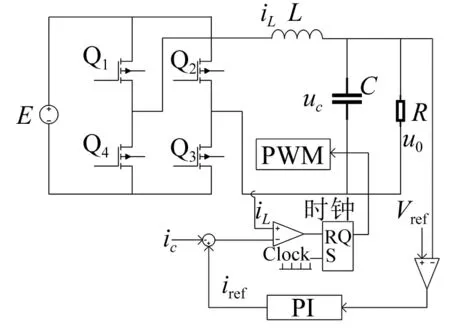
图1 逆变器原理图

状态1的状态方程:

(1)

状态2的状态方程：

(2)

式中：iL为电感L电流；uc为电容C电流；E为直流侧电压。

2 斜坡补偿在峰值型电流逆变器的应用

DC/DC变换器通过斜坡补偿抑制不稳定现象[5-6]，对于峰值型电流逆变器同样可以采用这种方法，以提高系统运行的稳定性。在峰值电流控制的逆变器中，当占空比较大时，会出现倍周期分岔现象[7]。为了使变换器运行在稳定状态，可以采用加入斜波控制来抑制倍周期分岔现象。斜波补偿的电感电流图如图2所示。

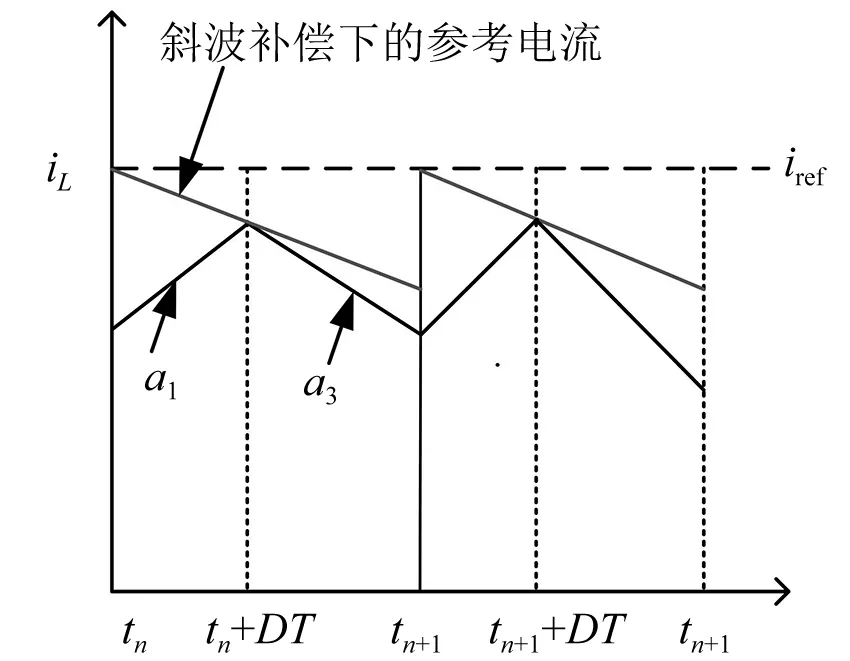
图2 斜坡补偿下的电感电流图

(3)

(4)

式中:ω为角频率，ω=2πf；f为工频；Vrefsinωt为电压外环参考电压。

根据几何关系，加入斜率为-k的斜坡控制之后，经过一个周期电流：

(5)

式中:Δi为在tn时刻加入的扰动电流。

经过一个周期T后Δi变为Δi1，经过n个周期后：

(6)

式中:Δi经过n个周期T变为Δin。

为使补偿后的扰动最终变为0，需要满足

(7)

当满足

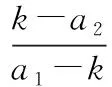
(8)

此时为逆变器进入倍周期分岔的临界点。加入斜率为Sramp的锯齿波，此时斜率k为：

(9)

代入式(8)后：

(10)

电源输出的功率等于电阻所消耗的功率，即

(11)

将式(11)代入式(10)后得到

(12)

将kc=Sramp·T代入式(12)，其中kc为加入的斜坡补偿的幅值。得到：

(13)

3 Jacobian矩阵法对峰值逆变器的建模与分析

系统的稳定性可以通过Jacobian矩阵的最大模特征值来判断。逆变器根据状态得到在第n个周期，系统的稳态方程为：

(14)

式中:f-(x)为状态1对应稳态方程；A1、B1为状态1对应的状态矩阵；f+(x)为状态2对应稳态方程；A2、B2为状态2对应的状态矩阵；x为状态变量(电感电流iL和电容电压uc)。

假设一个切换面u(x,t)=0，状态变量满足切换面时，工作状态发生变化，切换面与斜坡的补偿大小有关。假设切换面的解为：

(15)

式中:Φi为第i个状态转移矩阵；Bi为在第i个状态下的系数矩阵。

在第n个周期，状态变量的变化如图3所示。

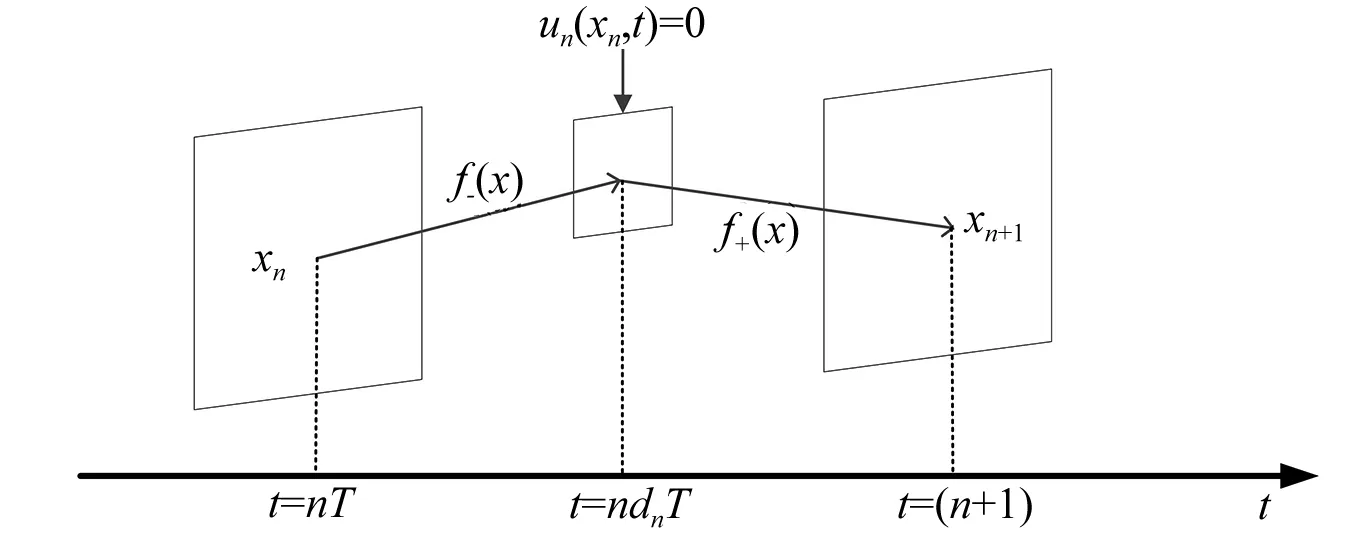
图3 状态变量变化图

该变换器的离散模型为：

xn+1=Φ[Φ(xn,dnT),T-dnT]

(16)

式中:xn+1为经过n+1个T后的状态变量；Φ为系统的转移矩阵；xn为经过n个T后的状态变量；dn为第n个周期开关的占空比。

第n个开关周期的Jacobian矩阵为：

(17)

式中:xPn、xDn、DnT为系统的稳态工作点。

当系统处于稳态时，因为开关的频率远远大于工频频率，稳定点满足式(18)：

(18)

其中

(19)

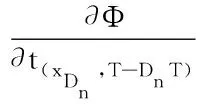
(20)

(21)

当加入斜坡控制之后，切换面：

u(x,t)=iref-iL-ic

(22)

式中:ic为加入的斜坡补偿电流。

ic=kcmod(t/T,1)

(23)

通过泰勒公式一阶展开并代入f-和f+得到：

(24)

峰值电流型逆变器出现分岔是因为参考电压的快速变化导致的。式(24)中的第一项近似为1，则在电路初始状态：

(25)

可得此时矩阵的特征值为：

(26)

由电路的特性可得λ1始终小于1，所以要抑制系统震需满足

(27)

即：

(28)

对于该逆变器当uc=Vref时，出现的分岔是最严重的，因此此时加入斜坡补偿即可有效抑制分岔。电路在n个周期内满足式(11)，将式(11)代入式(26)得到：

(29)

4 仿真验证

建立施加斜坡补偿后，结合图1通过MATLAB进行仿真。仿真电路的参数见表1，仿真控制结果如图4、图5所示。

表1 仿真电路参数

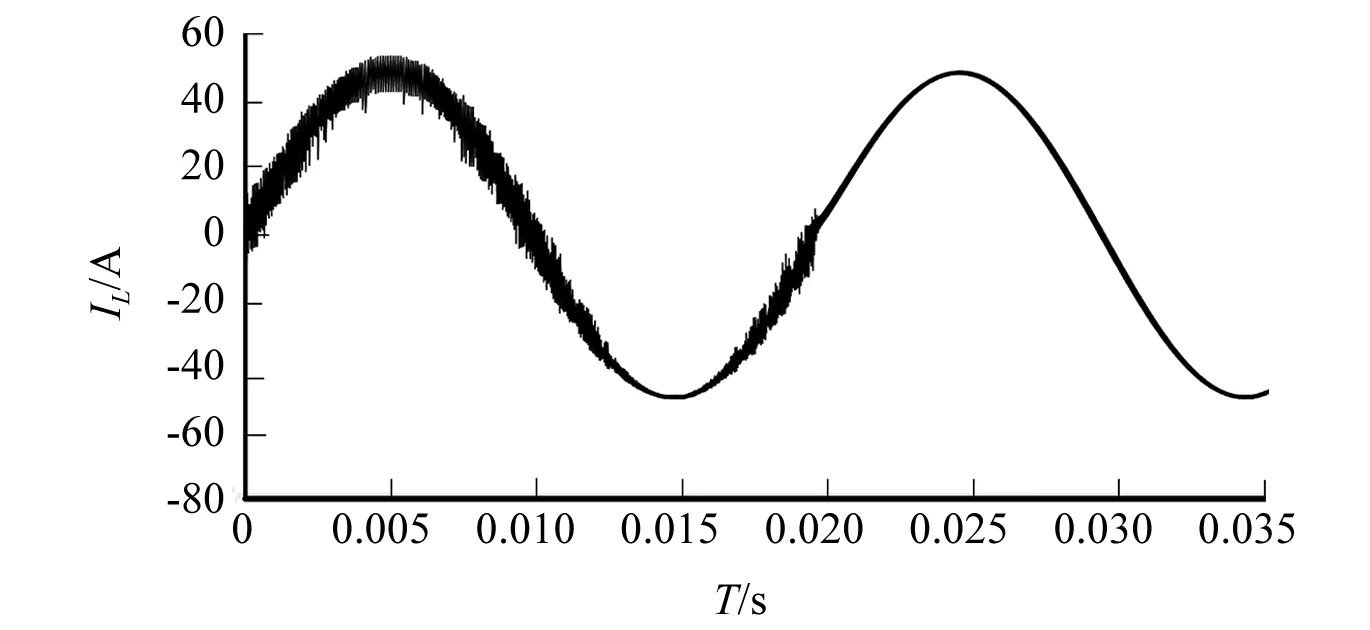
图4 加入斜坡控制前后电感电流图

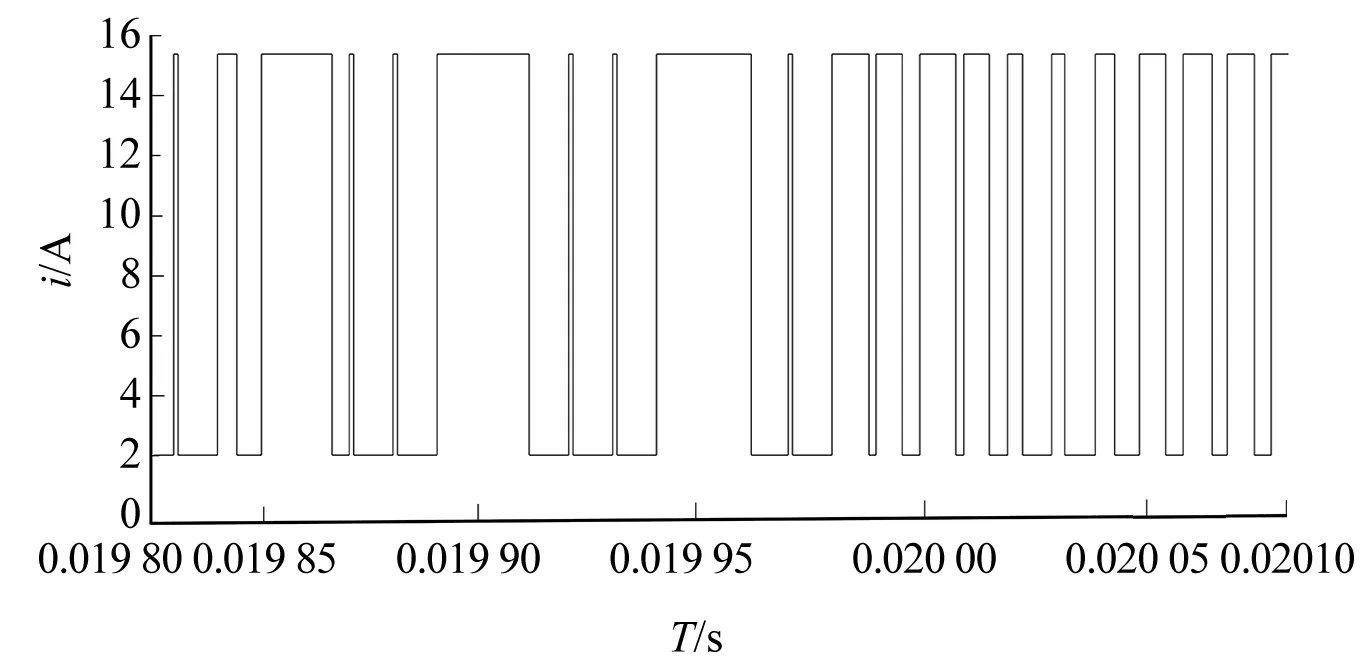
图5 加入斜坡控制前后占空比图

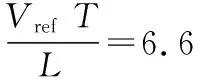
5 结束语

斜坡补偿是一种简单而有效的非线性行为的控制方法，它对控制对象有较好的适用性，适用于峰值电流控制的逆变器的分岔控制。本文从峰值电流控制的逆变器的非线性现象出发，对斜坡补偿峰值电流模式控制的H桥逆变器中的应用进行了详细分析。仿真结果表明斜坡补偿可以实现峰值电流型逆变器在占空比较大时的稳定运行，增强了电力系统的抗干扰能力。通过雅可比矩阵法建立离散数学模型，对雅可比矩阵特征值的分析得到斜坡补偿的最优解，给出了斜坡补偿的理论依据，计算的结果和仿真试验的结果是一致的。斜波补偿有效地抑制了倍周期分岔，对于峰值电流型逆变器的合理设计有了理论依据。