基于动态规划的备自投投入策略优化研究

冯豆， 刘邦， 曲鸿春, 王康， 姚庭镜， 王高洁

(国网亳州供电公司，安徽 亳州 236800)

0 引 言

伴随配电网规模的日益扩大，备用电源自动投入装置(busbar automatic transfer switch, BATS)的合理配置及相应投退策略的开发对经济性有着正向影响。基于国内BATS配置设计规范，合理的投入策略需兼顾BATS上下级之间的配合关系：典型BATS配合方式可分为“自下而上”和“自上而下”两类，基于电压等级进行投入动作时间的整定，必要时也需与线路、主变等保护进行折衷处理[1]。苏宜强等[2]通过分析各主变性能差异研究了BATS动作配合对事故后主变负荷的影响，并引入BATS次日停用系数和紧急停用系数实现单个BATS投退控制的约束，但BATS间的动作组合有效性未能充分体现。为实现系统中上下级的BATS配合方案，刘若溪等[3]通过厘清各BATS装置位置矩阵，并设定假想故障构建了故障与BATS动作组合之间的初步映射关系，重新设计了一种用于实时在线优化BATS投退组合的算法，能适应多种电网拓扑结构下的故障处理 。此外，N-1准则被广泛应用于电网静态安全性评估之中，利用N-1准则定义的BATS投入策略可全面考虑越限约束[4]。李俊格等[5]通过能量管理系统改善了BATS负荷高峰时段的退出问题，系统可通过获取电网运行信息并构建在线BATS模型，计及N-1静态安全因素，最后可完成投退组合的优化和自动闭环控制，但N-1校核算法遍历速度慢也制约着该方案的普及。综上，目前BATS投入策略对上下级配合、N-1静态安全约束和优化算法等研究处于割裂状态，如何通盘考虑诸多因素以提升电网的负荷转供能力，仍需进一步研究。

1 BATS现有策略规则

1.1 BATS与N-1故障关联集

BATS动作可看作电网中实际故障的自动响应，其关联关系受过载或越限条件约束[6-7]。基于N-1原则投退控制思路如图1所示，即以每一个N-1故障为起始点，并对关联BATS动作后的电网状态进行核验，如此循环遍历N-1故障集中的所有故障。

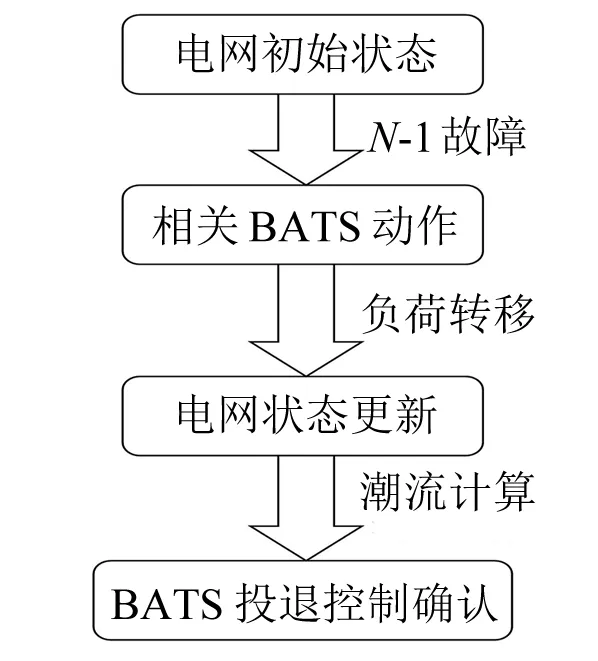
图1 基于N-1准则BATS投退控制

辐射状区域电网中，N-1故障常与BATS动作呈一对多的对应关系。根据负荷优先级和转移负荷能力等额外约束可找出N-1故障下的最优BATS动作组合，其关联矩阵通常可表征为：

(1)

式中：Bi,j为第i个N-1故障对应的第j个BATS状态，其中0、1分别表示BATS闭锁、投入状态。

1.2 多电压等级BATS动作顺序

BATS与N-1故障关联矩阵确定了任一N-1故障发生时BATS的动作组合，但BATS间的动作延时却有较大差异[8-9]。目前区域电网中多采用自上而下的BATS动作顺序，即上级(高压侧)BATS较下级(低压侧)BATS的动作整定时间短，如果上级BATS动作有效则不需要下级BATS再动作[10]。但无论是自上而下，抑或是自下而上的动作顺序均存在固有局限：自上而下的方式具有BATS调整量小和故障处理时间短的优势，但也易导致元件过载的可能性；自下而上的方式可有效避免上级变电站出现过载，但若是故障出现在上级变电站处，则存在多电压级下BATS装置相继动作。此外，区域电网大量使用T形接线形式，这也使得BATS电压等级相同和所处变电站不同而造成的动作分级紊乱情况频发。以图2为例，假设A线断开，各BATS均会因母线失电而触发动作条件，而在自上而下的动作顺序下，BATS1动作优先级最高。实际中，BATS1动作后可恢复母线1、2的供电，但母线3仍处于失电状态，此情况下BATS1、BATS3应同时动作。因此，仅根据母线电压等级区分BATS上下级顺序并不合理，其动作等级矩阵更应考虑T接线的特殊情况。

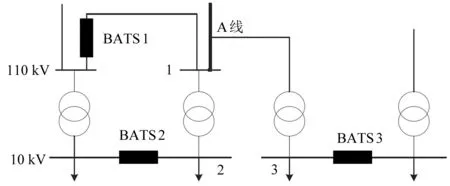
图2 T接线下BATS典型配置

电气系统中，下级母线需经过与其关联的上级母线以获得电源。如图2所示，假设BATS1备用母线1失电，则母线2同时也失去电源，由此也可判断母线1为母线2的上级母线，而根据母线与BATS之间的映射关系，也能得出BATS1为BATS2的上级BATS。

2 BATS投入策略优化算法

2.1 方法简介

鉴于动作BATS组合仍需基于电网拓扑结构兼顾动作时序、动作有效性等因素，故障发生后的BATS投入方式的获得，不仅是一个多参数、多目标的优化问题，还需综合考虑动作次数和负荷转供能力等方面。如图3所示，遍历组合通过搜寻所有可能动作组合，并综合动作次数、动作登记进行排序和校核，直至模型可输出满足实际需求的第一个解作为最优解。遍历组合可通过自定义的评价系数实现全局计算校核，但优化结果的好坏却与评价系数的定义息息相关。

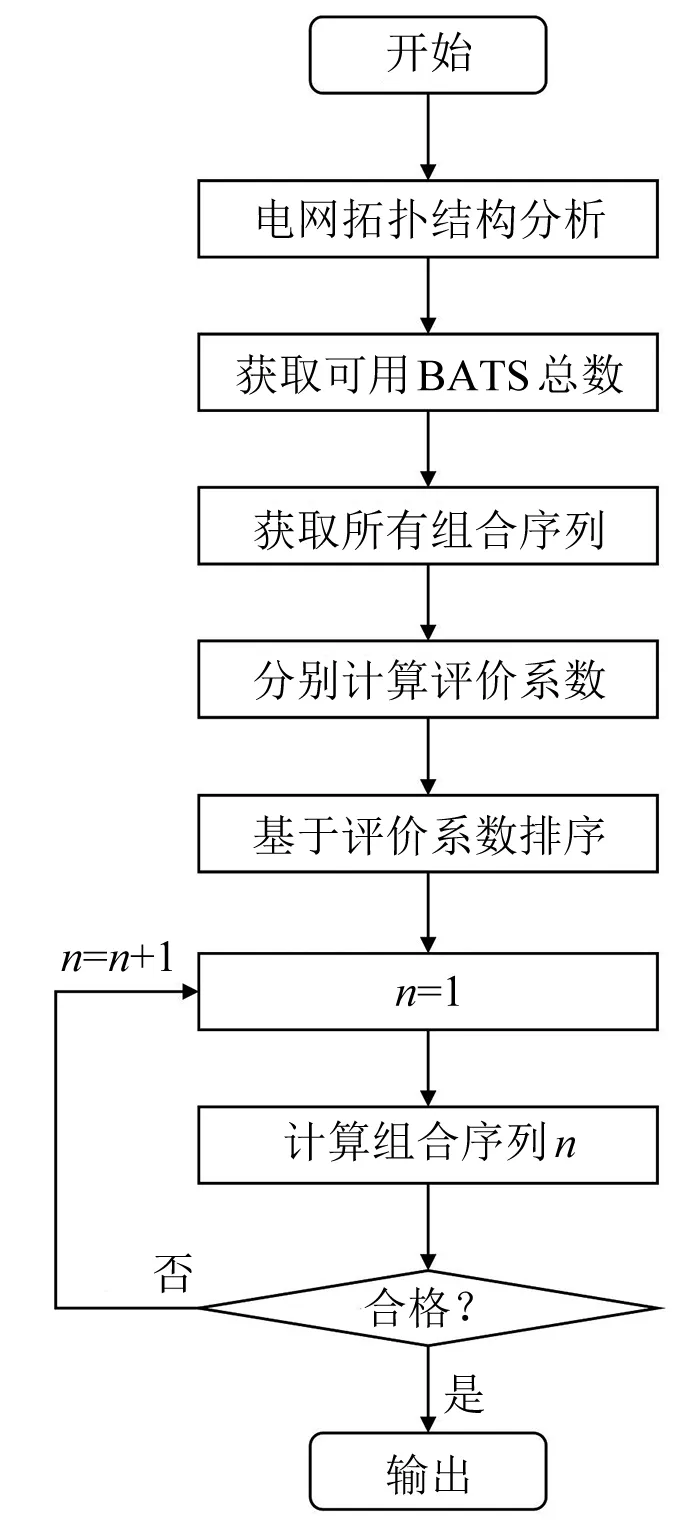
图3 全局遍历优化流程

图4中的遗传算法可生成多个“种子”动作组合，并基于其计算结果迭代“下一代”动作组合，其结果收敛情况与种子数、迭代次数有直接关系，这也加大了该方式的实用风险。

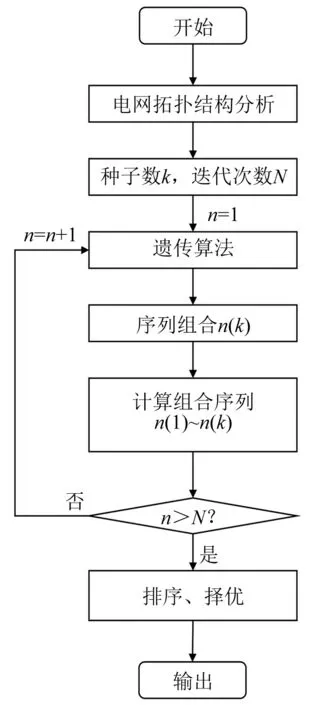
图4 遗传算法优化流程

本文研究了基于动态规划和全局评价系数分阶段遍历的可行性。动态规划多用于多阶段和多决策动态行为的优化领域，与本文BATS主体的投入动作、动作时序和动作次数等组合形式不谋而合。假设需进行N次动作BATS，可将每次BATS动作视为一个阶段，每一次选择视为该阶段中的决策，由此便能将N次BATS动作最优时序求解转化为动态规划模型，可兼顾“自上而下”和“自下而上”两种动作顺序的优化。如图5所示，动态规划无需对所有阶段(N次)进行完整遍历，实际中为减少BATS动作数量，若是遍历到n阶段之后便可达到优化收敛，即可提前停止计算。

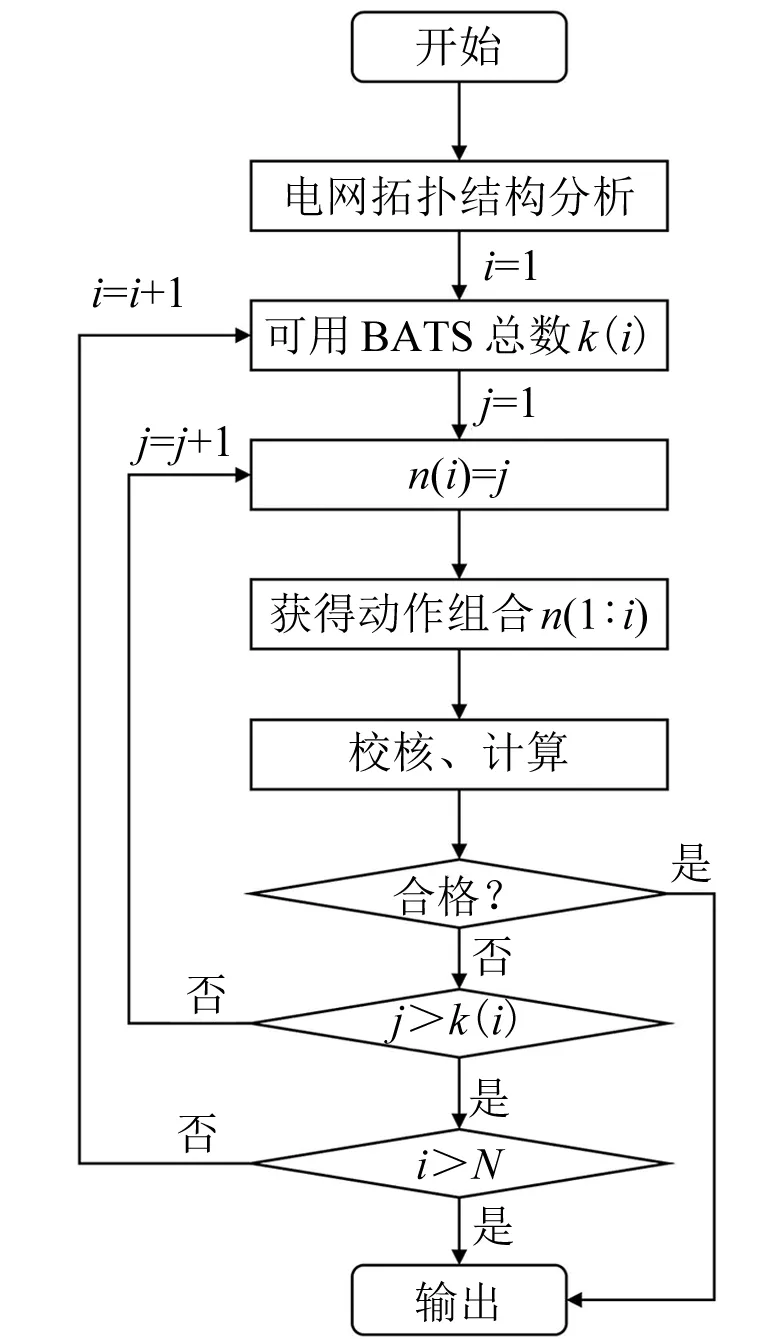
图5 动态规划优化流程

2.2 目标函数

1) 切负荷量最少

即确保过负荷有效解决的前提下，构建切负荷量最少的函数目标：

(2)

式中：m为切除负荷的数量；Pi为第i个N-1故障对应的负荷量；PK为过负荷量。

2) 电网损耗最低

BATS动作组合发生后，区域电网拓扑结构出现变化，此时区域电网损耗极值为：

(3)

式中：n为电网所有负荷线路的总数；Si为BATS开关状态，即开关合位为1，分位为0；Ri为线路电阻；Pi、Qi分别为有功、无功功率；Ui为电压幅值。

3) 动作次数最少

BATS动作会导致电网运行方式、线路潮流随之变化，因此降低区域电网BATS动作次数也可提升组合策略的有效性。

(4)

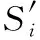
为对BATS投入策略方案进行优劣区分，可对切负荷量、电网损耗和动作次数极值求解。通过设定权重系数，将此多目标优化问题整合为一个目标函数，其中切负荷量和动作次数优先级最高。

F(x)=0.4×f1(x)+0.2×f2(x)+0.4×f3(x)

(5)

式中：f1(x)、f2(x)和f3(x)分别为切负荷量、电网损耗和动作次数的函数式最小值；F(x)为优化目标函数。

2.3 约束条件

BATS动作后的电网拓扑结构更新需进行相应的阶段潮流计算，并对母线电压、支路电流及功率越限情况进行甄别。此外，联络线转供容量和主变压器容量也是策略优化中的重点约束目标。

1) 联络线转供容量约束

Aij≤Cij

(6)

式中：Aij为故障供电单元i通过第j个联络线开关所在的联络线转带的负荷；Cij为所在联络线转带的最大负荷容量。

2)主变压器容量约束

Gi+Ci≤Li

(7)

式中：Gi为供电单元i中主变原有分负荷；Ci为主变所转带负荷；Li为主变额定容量。

2.4 优化流程分析

BATS投入策略优化为含有约束的非线性模型，为此本文提出了基于动态规划的BATS投入优化流程，相比单一全局遍历效果更佳，如图6所示。首先基于区域电网拓扑结构形成N-1故障集合，结合母线失电的思路寻出其关联的BATS组合集，并对动作优先级展开排序；随后对BATS动作后的电网进行潮流计算，结合目标函数的极值求解寻得策略最优解；最后根据约束边界，确定此投退状态结果的合理性。

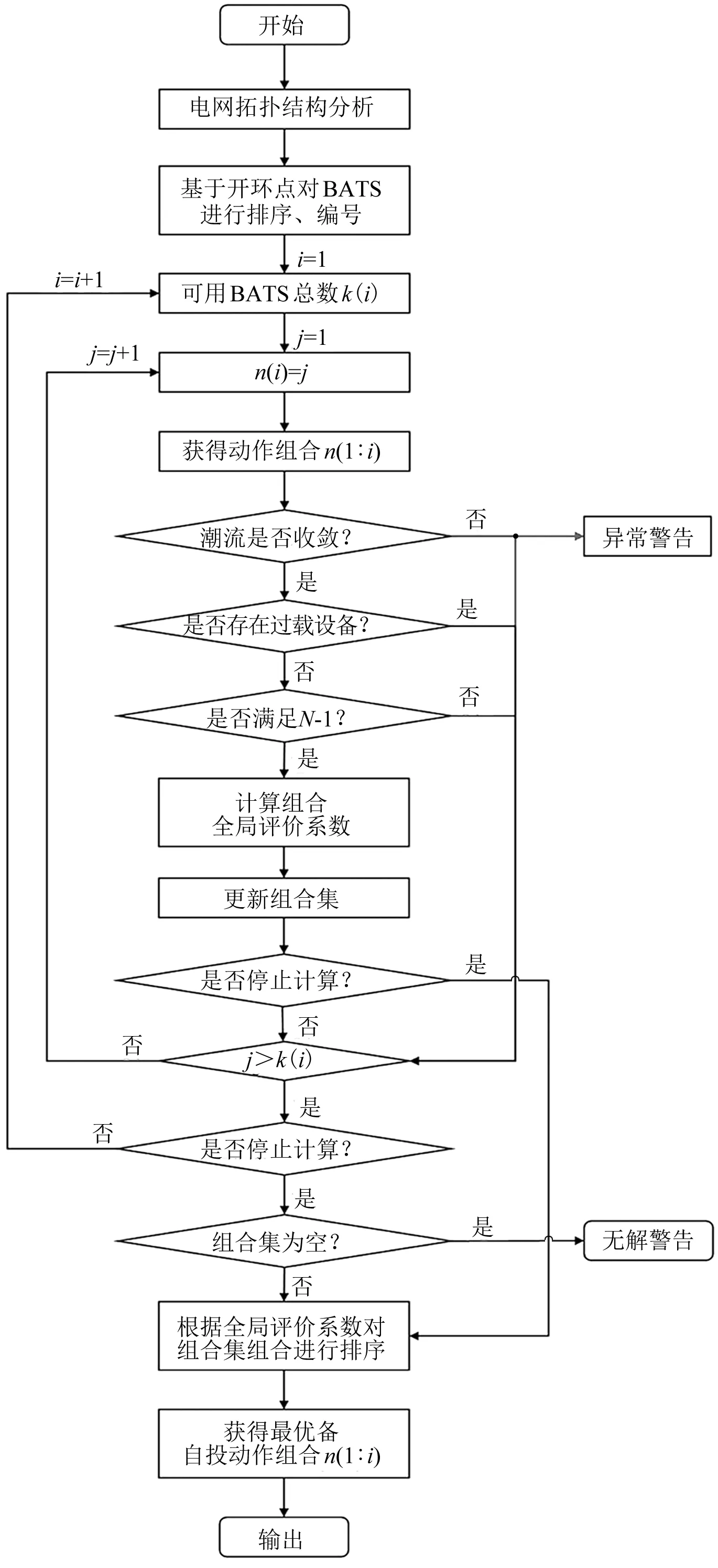
图6 基于动态规划的BATS投入策略

以蒙城生物电厂望月变35 kV线路为例，其全长近3.6 km。望月变六回35 kV出线均配置有RCS9611型BATS装置，线路两侧设有全线速断的电流差动保护。利用典型全局遍历、遗传算法及动态规划对BATS投入策略进行优化汇总，发现动态规划、遗传算法和全局遍历收敛速度以此递减，如图7所示，动态规划可有效规避局部收敛的同时，系统转供能力较遗传算法提升3.5%，且N-1潮流及电压无越限现象。

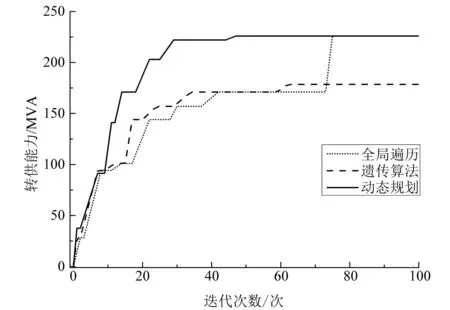
图7 算法收敛对比

3 结束语

(1) 基于N-1准则的BATS投入策略优化需兼顾动作组合与动作顺序之间的配合，而采用BATS与N-1故障关联矩阵能快速定义全网BATS状态，通过区域电网拓扑结构可方便定义BATS间的上下级关系。

(2) 基于动态规划理念的BATS投入策略优化可全面反映目标函数极值与约束极限限制间的trade-off关系，精度效果和计算速度更佳，也为实际配电网中的BATS动作规范提供了参考。