安徽怀宁某地区地应力测量结果及其构造分析

王昌举，周文渊，鞠远江，孙如华

（徐州中矿岩土技术股份有限公司，江苏徐州 221116）

0 引言

地应力是存在于岩体内部的应力，与地壳浅部和深部发生的构造作用以及派生的内动力地质灾害具有密切的关联。地应力场的状态对构造运动和地壳运动起着重要的作用。探究区域地应力场状态对了解当地的构造运动、区域地壳稳定性以及地质灾害发生的机理具有重要的意义。地应力是导致地下工程事故的主要原因，同时也是进行地下围岩稳定性分析、工程开挖设计以及正确策略指导的重要前提[1]。地应力分析在隧道设计施工、深部资源勘探开发等工作中具有广泛的应用，是工程地质、深部能源等领域的重要研究课题[2～3]。

本次测试地点位于安徽怀宁某地区，测试方法为水压致裂法。水压致裂法属于对地应力的直接测量法，可以直接获取地应力具体量值以及方向，两者是分析地区区域稳定性时所需的重要基础数据。本文针对该地区浅部深度进行水压致裂，获取其地应力值并进行分析，并对该地区域构造特征进行探讨。

1 区域构造特征

测试地区地属半丘陵浅山区和半圩畈区，三面浅山环绕。区域构造位置位于扬子板块长江中下游坳陷带中段北侧，其南为江南隆起带。该处围绕北东向展布的董岭群变质基底，震旦系至中三叠统海相盖层呈现为北东向的背形构造。该背形构造西北侧为白垩纪—古近纪陆相潜山断陷盆地，东南侧为同时代的望江陆相断陷盆地。区内董岭群变质基底周边海相盖层所呈现的北东向褶皱与走向逆断层是印支期前陆变形的产物。这些走向逆断层都向南东倾，造成了多处地层的重复。海相盖层内还发育了一系列北西走向的正断层，垂直于褶皱的走向，皆向北东倾，应为印支期褶皱中的横向正断层。区内南侧与西北侧被陆相断陷盆地所覆盖。南侧下白垩统汪公庙组红色碎屑岩所充填的断陷盆地是望江盆地的一部分，在区内受近东西向、南倾正断层所控制。西北侧上叠的断陷盆地内为上白垩统浦口组、赤山组红层所充填，为北东向潜山盆地的一部分，在区内受北东走向、向北西倾的正断层控制。

测区东西侧均分布有北东走向的长大型节理，西侧有一近似南北走向的压扭性断裂，东侧有一北西向走向的逆断层。测试区有三条主要水系，西侧的水系自南向北流经该区域，在该区的北部偏向北东；东侧的水系自南向北经过该区域，在区域北侧与西侧的水系交汇。两水系之间存在一条南北向的水系。区域内的断层以及河谷走向均会对地应力状态造成影响，断层附近的地应力分布状态会受到明显的扰动，在断层端部、拐角处以及交汇处，会出现应力集中的现象；河谷地区对局部地应力场的方向和大小均有影响，在靠近河谷的区域，最大主应力方向可能会与河谷的走向近于垂直。

2 水压致裂法试验介绍

本次实测地应力选取的是传统水压致裂法（HF），即利用水力压裂测得钻孔截面上的二维地应力状态。该方法是国际岩石力学学会试验方法委员会颁布的确定岩石应力建议方法中所推荐的方法之一[4]，是目前国际上能较好地直接进行深孔应力测量的先进方法。

除去传统测围岩二维地应力状态的方法，也有基于多个（不少于3个）交汇的钻孔开展水压致裂的测三维地应力状态的方法[5]，属于多值测量，测值方程的数目大于6个，利用数理统计的最小二乘法，求解得到应力分量最佳值的方程组[6]。但此方法在实际应用中具有很大的限制：一是在围岩完整度较低、节理化较高的情况下，孔内的次主应力难以准确获得；二是在地应力较为均一的地区，围岩破裂的走向具有较大的随机性，难以获得恰好沿最大次主应力方向延伸的裂隙；三是由于非垂直孔钻孔方向难以与某一主应力平行，实测中围岩会存在剪切应力，在后续确定应力的计算时需要进行修正。

另外还有基于原生裂隙和单钻孔的水压致裂法，称为原生裂隙水压致裂法（HTPF），也是一种三维地应力测试的方法。原生裂隙水压致裂法相较于传统水压致裂法，在利用封隔器封隔致裂段时，需要同时封隔出一条闭合状态的原生裂隙，利用高压水流使原生裂隙张开，在后端的计算机上利用压力-时间曲线获得作用在原生裂隙上的法向应力，需要完成至少6组测试，且每组原生裂隙的走向和倾角完全不同，就可求得所测点位的地应力。此种方法有效地利用到了原生裂隙，但在实测中所需的原生裂隙数目较多且产状需完全不同，具有局限性。

水压致裂的理论最初起源于石油天然气开采领域,美国的Hubbert和Willis认为水力压裂出的裂隙与地应力之间存在关系[7]；再后来，建立在大量研究工作的基础上，Scheidegger第一次提出将水压致裂应用于地应力测量具有可能性[8]；直到1967年，Haimson 和Fairhurst提出了水压致裂用于测量地应力的基础理论[9]，同时在理论和实验两个方面进行了完善[10]。1980年，Cornet等[11～13]提出了利用原生裂隙的注水测试来确定原地应力的方法。在第一届国际岩石应力研讨会上，Cornet[14]正式将这种方法命名为HTPF法。

水压致裂法在我国具体应用的时间较晚，20世纪80年代由李方全等[15]在河北易县首次开展了水压致裂法对地应力的测量工作；传统水压致裂法理论建立在平面应变理论上，针对此现状，1991年刘允芳[6]引入了水压致裂三孔交汇三维地应力测量；1999年罗超文[16]在水布垭水电站首次进行了水压致裂三孔交汇三维地应力测量；刘允芳[17]介绍了原生裂隙水压致裂法三维地应力测量，该法利用关闭压力确定裂隙法向应力，理论上测量精度更高；景锋[18]发现，原生裂隙水压致裂法三维地应力测量所得地应力信息尺度大，较适合大型工程区应力场研究，推导了更便捷的计算过程。

水压致裂法具有可测量深度大、测量结果整理时不需要岩石弹性参数参与计算，可以避免因岩石弹性参数取值不准引起的误差，且岩壁受力范围较广(钻孔承压段程度可达1～2 m)。本次所选孔位内部围岩裂隙较少，且难以开展斜向钻孔。原生裂隙三维水压致裂法和多孔三维水压致裂法相较于传统水压致裂法具有局限性，传统水压致裂法可以避免“点”应力状态的局限性和地质条件不均匀性的影响，相比于另外两种方法具有操作简单，测试周期短等特点。传统水压致裂法对地应力测量有单回路和双回路两种测试系统，本次测试中选择的为单回路测试系统，相比于双回路测试系统，单回路测试系统更适用于较深和口径较小的钻孔。

2.1 水压致裂法基本原理

测量时首先取一段基岩裸露的钻孔，用封隔器将上下两端密封起来；然后注入液体，加压直到孔壁破裂，记录压力随时间的变化，并用印模器或井下电视观测破裂方位。根据记录的破裂压力、关泵压力和破裂方位，利用相应的公式算出应力的大小和方向。水压致裂法对地应力测量原理以弹性力学为基础，并且依据于下面三个假设：

（1）周边岩壁是线性、均匀、各向同性的弹性体。

（2）当围岩为多孔介质时，注入的液体在介质中的流动遵循达西定律。

（3）岩体中地应力的一个主方向为垂直方向，和垂直向测孔一致，大小和上覆岩层压力相同。

基于上述的假设，水压致裂法的计算模型（图1）可以简化为以下形式。

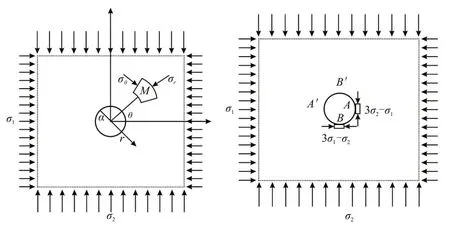
图1 水压致裂测量应力的力学模型Figure 1. Mechanical model of hydraulic fracturing for stress measurement

一个半径为a的圆孔上作用两个主应力σ1和σ2，圆孔位于一个无限大的平面上，根据受力分析，圆孔外的任意一点M处的应力有：

式中：σr为M点的径向应力；σθ为M点的切向应力；τrθ为剪应力；r为M点到圆孔中心的距离。

当r=a时，此时的应力状态为孔壁上的状态：

当角度为0°或180°时有：

图2 为压力随时间的变化曲线。下面选取ZK-55钻孔的某一深度介绍参数的处理。

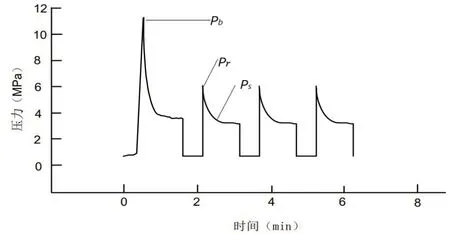
图2 压裂曲线Figure 2. Fracturing curve

压力参数Pb、Pr、Ps和P0四个量为水压致裂法地应力测量计算地应力值的基本参数，一般根据压裂特征曲线选取。破裂压力Pb为第一次压裂循环阶段中的峰值；重张压力Pr为第二次和之后的循环曲线压力上升部分拐点处的压力；瞬时关闭压力Ps为破裂压力和重张压力之后压裂循环曲线下降部分拐点处的压力；孔隙压力P0可以采用孔隙水压力计测量来确定。实验结果表明，一般情况下岩体中的孔隙压力大致和当地静水压力相当，在没有实测数据的情况下，可用当地静水压力替代。

水压致裂法对地应力测量采用的理论为最大单轴拉应力破坏准则，此时轴向应力仅和地应力状态有关。对围岩破裂起到控制作用的是切向应力σθ，当孔内承压段注液受压后，切向应力σθ减小，直至转换为拉应力状态。进行地应力测量时，拉应力最大的部位为破裂缝产生的位置，在钻孔壁极角θ=0或θ=π时，也就是最大主应力方向。钻孔壁的切向应力最小为：

由（4）式可得，当液压增加时，钻孔岩壁切向应力σθ逐渐下降为拉应力状态，随着液压Pw的增加，拉应力也逐渐增加，当拉应力等于或大于围岩的抗拉强度σt时，钻孔岩壁出现裂缝，这时承压段的液压就是破裂压力Pb。因此，钻孔承压段周围岩壁围岩产生破裂(不考虑孔隙水压力)的应力条件为：

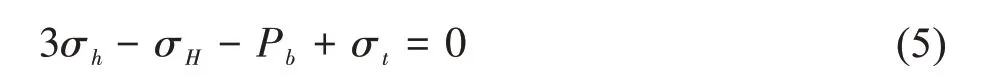
在深层岩体中，还存在孔隙水压力P0，因此，岩体中的有效应力为σ-P0。考虑岩体中的孔隙水压力等作用，钻孔承压段周围岩壁围岩产生破裂的应力条件为：

式中：K为孔隙渗透弹性参数，可在实验室内确定，其变化范围为1 ≤K≤2。对非渗透性岩石，K值近似等于1，则上式可简化为：

钻孔岩壁破裂以后，关闭压裂泵，此时维持裂缝张开的瞬时关闭压力Ps同裂纹面相垂直的最小水平主应力σh达到平衡：

此时最大主应力为：

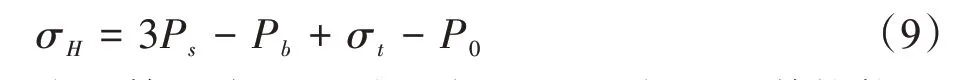
由于第一次施压时围岩已经破裂，所以其抗拉强度近似于0，根据式（7），重张压力为：

所以：

（1）钢纤维混凝土拌和采用的是强制式搅拌设备进行，材料的投入顺序为：砂→纤维→碎石→水泥加入搅拌罐，并且进行1min的干拌，之后搅拌3min。

静水压力P0为：

垂直应力σv为：

岩石容重γ取26.5 kN/m3。

2.2 测点布置

本次安徽怀宁某地区的地应力测试选择的钻孔为ZK-55，测点的岩体整体上都较完整，实验过程中选取了完整性相对最好的测试段进行水压致裂，以减少原生裂隙对实测数据的干扰。测孔选择10个测点，由浅至深，同时结合前人在此地区的3个测孔（分别为ZK-01、ZK-08、ZK-13）数据加以整合。具体测点信息见表1。

表1 各测点及其深度Table 1. Each measuring point and its depth

2.3 仪器设备

测量设备采用SY 型新型单回路地应力测量系统。本系统改进单回路是利用钻杆连接测试系统，通过高压管、钻杆向系统施压，井下通过单向逆止阀控制，在使封隔器座封并稳定后，对两封隔器中间部位进行注水加压进行井段压裂。单回路系统测试过程简易，管路压力损失少，可更好保障测试结果的准确性。图3为测试系统及其组成部分。

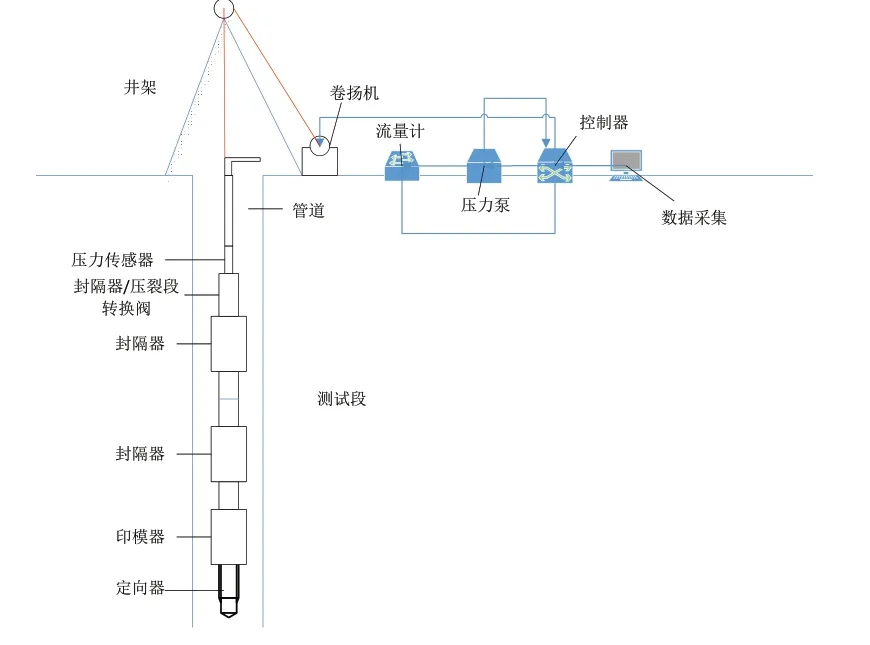
图3 测试系统Figure 3. Test system

3 测量结果

3.1 地应力测量值

依据上述的处理过程，将4 个钻孔共计40 个点的数据分别按照深度制作曲线。图4、图5、图6、图7 为各个钻孔的破裂压力Pb、重张压力Pr、瞬时关闭压力Ps随着深度变化的折线图。

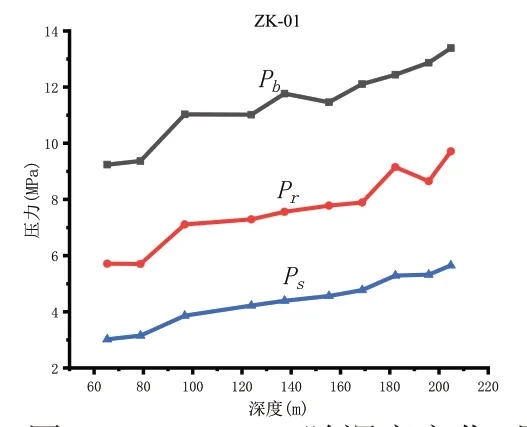
图4 Pb、Pr、Ps随深度变化曲线（ZK-01）Figure 4. Pb,Pr and Ps values changing with depth（ZK-01）

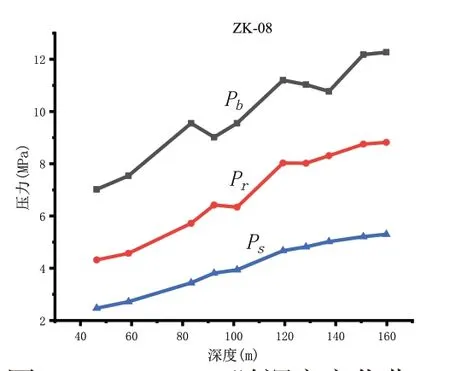
图5 Pb、Pr、Ps随深度变化曲线（ZK-08）Figure 5. Pb,Pr and Ps values changing with depth（ZK-08）

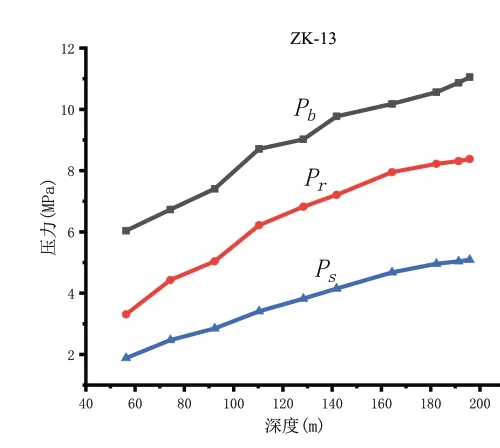
图6 Pb、Pr、Ps随深度变化曲线（ZK-13）Figure 6. Pb,Pr and Ps values changing with depth（ZK-13）

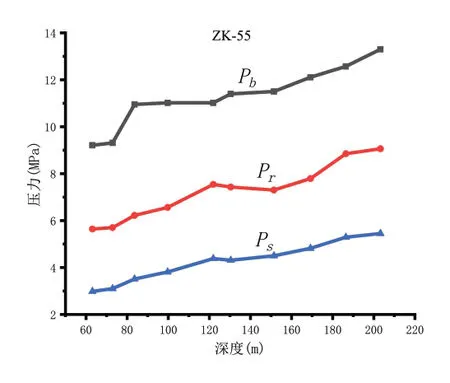
图7 Pb、Pr、Ps随深度变化曲线（ZK-55）Figure 7. Pb,Pr and Ps values changing with depth（ZK-55）

由上图可知，破裂压力Pb、重张压力Pr、瞬时关闭压力Ps均是随着深度变大而同时增大。

依据式8、式11、式13 可得出各个位置的大小主应力和垂直应力。下图为大小主应力和垂直应力随深度变化的折线图，如图8、图9、图10、图11。

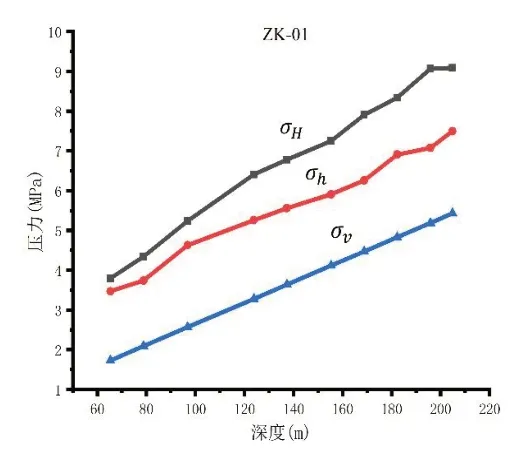
图8 σH、σh、σv随深度变化曲线（ZK-01）Figure 8. σH,σh and σv values changing with depth（ZK-01）

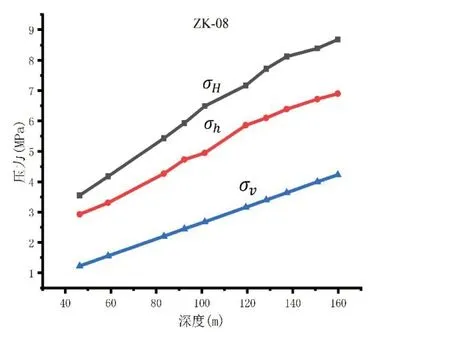
图9 σH、σh、σv随深度变化曲线（ZK-08）Figure 9. σH,σh and σv values changing with depth（ZK-08）

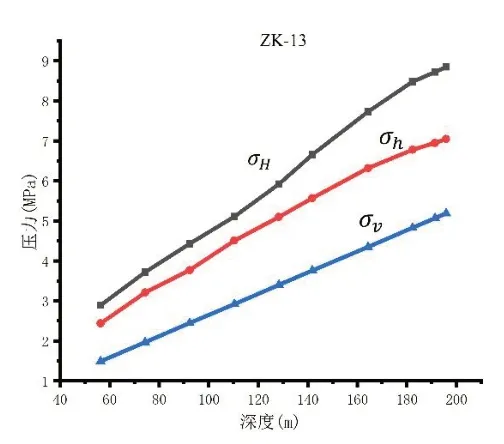
图10 σH、σh、σv随深度变化曲线（ZK-13）Figure 10. σH,σh and σv values changing with depth（ZK-13）

图11 σH、σh、σv随深度变化曲线（ZK-55）Figure 11. σH,σh and σv values changing with depth（ZK-55）

表2 为各个钻孔大小主应力值随深度变化关系的线性拟合结果。

表2 大小主应力同深度的拟合结果Table 2. Fitting results of maximum and minimum principal stresses changing with depth

最大主应力与深度的线性相关系数最大为0.99，最小为0.98；最小主应力与深度的线性相关系数最大为0.99，最小为0.98。大小主应力随深度变化趋势明显，总体上呈现随深度线性增加的趋势。

3.2 方向角测量值

为了获取最大主应力的方位，采用印模的方案进行测量。基本原理是利用印模器将压裂后孔壁上的裂隙痕迹印下来。整套系统由印模器和自动定向仪组成，印模器与压裂阶段的封隔段相同，在封隔器外表涂上乳胶用以印模。测定方位角时，需要先将带有定向器的印模器下放到压裂段的深度，再通过地面的加压系统对封隔器进行加压使其膨胀，为了获取足够清晰的印模痕迹，需要对其施加足够大的高压，使得孔壁上压裂的裂隙重新张开，此时封隔器表面乳胶得以挤入其中，在保持足够的时间后，印模器表面就会出现同裂缝相对应的印迹。

定向器主要是由测角部件、电子罗盘、电子时钟等控制系统集合构成，在地面预设启动时间以及划定基线后，随印模器下放至印模点，在到达预设的时间后自动开启计时及测角。图12为定向器及其基线。

图12 定向器Figure 12. Orientator

印模结束后从孔内取出整个系统，将系统垂直放置，沿着印模器上的裂隙方向作垂直线段，延伸至定向器的底部，在放置定向器底部的纸张上标出线段的垂直投影点，同时标记出定向器上的基线投影点。图13为处理后的ZK-55印模图。

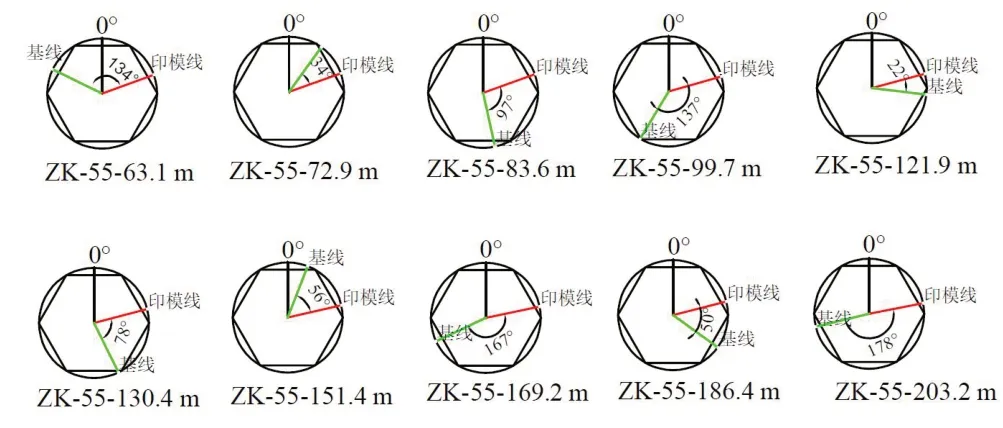
图13 ZK-55印模图Figure 13. Impression charts of ZK-55

用同样的方法对4 个钻孔的各自点位进行处理，得到表3。

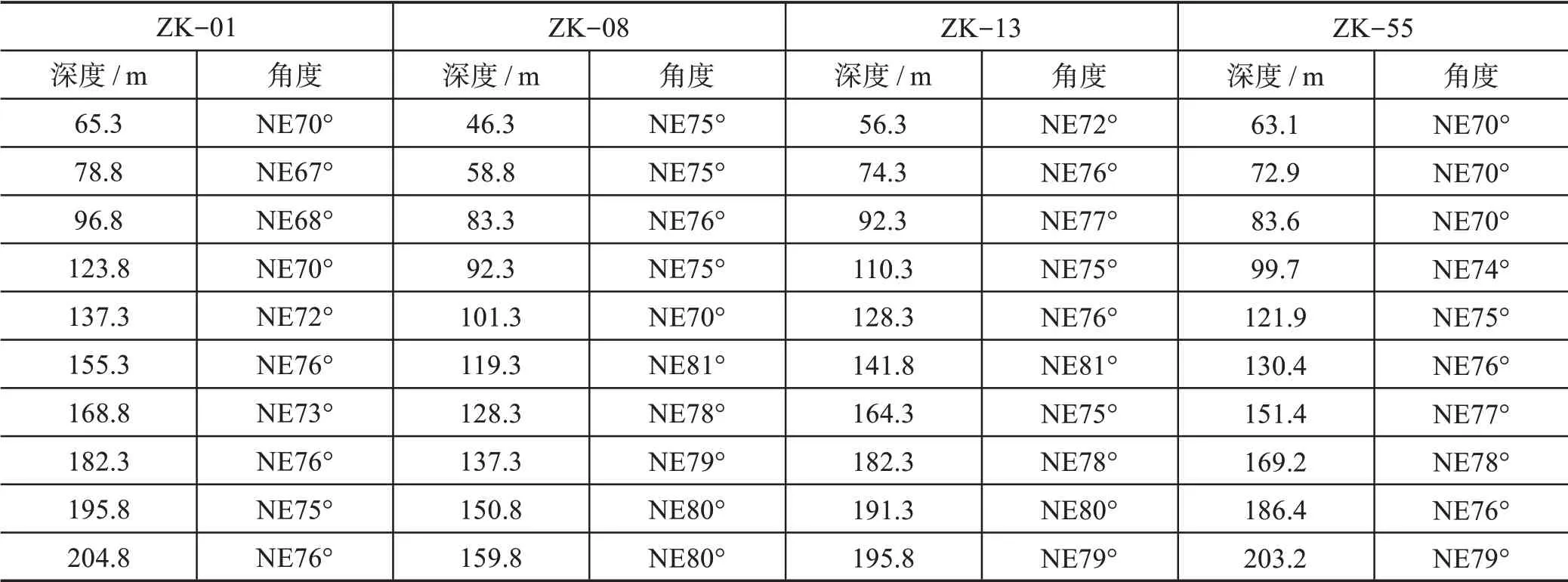
表3 大主应力方向汇总Table 3. Summary of maximum principal stress directions

结果为ZK-01 大主应力方向为北东72.3°左右；ZK-08 大主应力方向为北东76.9°左右；ZK-13 大主应力方向为北东76.9°左右；ZK-55 大主应力方向为北东74.5°左右。

4 结果分析

4.1 区域断裂与岩性分析

根据所测结果可以得知大主应力最大值为9.32 MPa，小主应力最大值为7.50 MPa。4个钻孔得出的数据均为水平应力大于垂直应力。地应力是一种存在于地层中未受扰动的天然应力，影响地应力的因素较多，但整体上构造应力场和重力应力场是地应力场的主要组成部分，即当地的区域地质构造（表现为水平向应力）和垂向上岩体的分布（表现为垂直向应力）是影响地应力的主要因素，如图8、图9、图10、图11 所示，有σH＞σh＞σv。同时，依据此前的大量实验数据，说明在浅层地壳中平均水平应力要普遍大于垂直应力，即水平方向上的构造运动对地壳浅层地应力形成起主要控制作用。在构造运动中，水平向运动起主导作用。

4个钻孔的大小主应力与中国地区的平均应力环境相比均为应力水平较高，景峰[19]通过搜集中国大陆地区450 多个钻孔的地应力实测资料，建立了大小应力随深度的分布图，并建立了回归方程：

式中：H单位为km；σH和σh单位为MPa。

4 个钻孔的最大深度分别为ZK-01（204.8 m）、ZK-08（159.8 m）、ZK-13（195.8 m）、ZK-55（203.2 m），代入方程内，最大主应力值分别为：6.784 MPa、6.783 MPa、6.784 MPa、6.784 MPa，最小主应力值为2.236 MPa、2.235 MPa、2.236 MPa、2.236 MPa。实测结果要远大于此估计值。根据现阶段对地应力的研究，地应力场主要受到板块运动、区域地质构造、地层岩性等因素影响。本次地应力测试数据较高可能与区域地质构造以及岩性相关。如图14所示，测试区存在着5条断层，所选钻孔均位于断层附近，断层附近的地应力分布状态会受到明显的扰动，特别当在断层端部、拐角处以及交汇处时，应力集中现象会愈加明显。

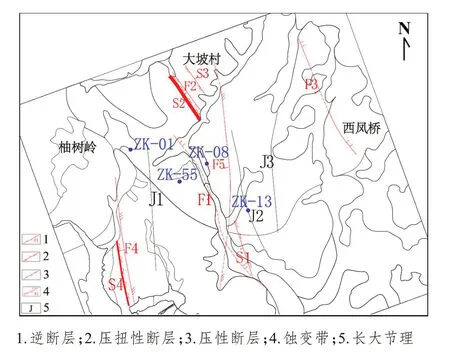
图14 区域构造图Figure 14. Map of regional structures

地应力作为赋存于岩体内部的内应力，必然会受到岩体的各项物理力学性质的影响，地应力状态的变化反过来又会影响围岩性质，二者相互作用。根据测点钻孔岩心得知，区内地层主要由花岗岩组成，花岗岩的弹性模量较大，并且所测段的岩心都较为完整，在岩体的完整性（RQD）较好时，地应力的最大主应力值同岩体的弹性模量呈正相关[20]。因此测点地区的岩性也是导致地应力大于中国地区最大主应力平均水平的因素之一。

4.2 区域构造分析

在大尺度的地应力场上，板块运动是导致其变化的最直接因素。中国地区的地应力状态主要受到太平洋板块、印度洋板块、欧亚板块以及菲律宾海板块之间相对运动的影响。由于太平洋板块向欧亚板块挤压的作用，菲律宾海板块北西向俯冲欧亚大陆产生的侧向挤压作用对中国东部沿海地区应力场也产生一定的影响；另外，印度-欧亚板块碰撞的远端效应也对中国东部的地应力场产生一定的影响，以致中国东部大陆现代构造应力场的主体特征表现为北东东向的挤压，与相邻板块俯冲的方向大体一致。本次测试地点位于长江中下游地区，秦岭-大别造山带南缘与扬子板块北缘之间，是扬子北缘复合构造带的东段，在汉江盆地以东的区域长江复合构造带上。区域构造主要受控于北东向走滑断层。本次地应力测试所测的大主应力方向分布为北东72°～76°，近垂直于测点所在的河谷走向，说明此片区的最大水平主应力优势方向为北东向，与区域构造线基本重合。此次共选取了4个点，选点之间每3 个点成三角形，通过分别对其分析，便可反映出该4个点所围成区域的地应力特征。

5 结论与建议

5.1 结论

（1）实测深度范围内ZK-55钻孔的大主应力最大值为9.32 MPa、小主应力最大值为7.48 MPa，大主应力方向为北东72.3°左右。

（2）实测的大小主应力均大于中国地区区域内的平均水平，可能是由于测点位于断层附近，以及花岗岩岩层的影响。

（3）场区内地应力以水平向的构造应力场为主，且随着深度的增加而增加，在局部范围内大小主应力变化会出现波动，整体上呈线性。

（4）实测此片区的最大水平主应力优势方向为北东向,与区域构造线重合。

（5）在后续开挖洞室时，洞轴线走向应当与所测的最大主应力方向尽量一致。

5.2 建议

一般认为当地下洞室洞轴线走向与最大主应力方向相平行时，隧道的稳定性较高，所以在后续的施工设计阶段应当使洞轴线方向最大程度地靠近最大主应力方向，这是提高洞室围岩稳定性以及减少洞室变形破坏的措施之一[21]。通常的地下线路选线原则为：在水平主应力大于垂直主应力时，洞室走向应该平行于水平最大主应力方向，或夹角在0°～30°；在水平主应力小于垂直主应力时，洞室走向应该平行于水平最小主应力方向，或夹角在0°～30°。此次安庆地区水压致裂的结果表明当地应力场主要以水平向为主，最大主应力方向大致为北东72°～76°，所以后续洞轴线走向应当尽量接近于此数值，更加利于洞室的稳定。