基于图像测量的Stewart 平台双阶控制技术

张良总，杨 涛，吴 云，唐 涛*

1 中国科学院光电技术研究所，四川 成都 610209；2 中国科学院光束控制重点实验室，四川 成都 610209；3 中国科学院大学，北京 100049

1 引言

空间望远镜广泛应用于天体目标观测和空间通信等场合[1]，然而由于空间中存在各种干扰，极大损失了光学载荷工作性能，同时降低了系统对目标的跟踪精度。已有的研究利用Stewart 平台的机械优势以解决此问题，如振动隔离和抑制系统(VISS)，卫星超静隔离技术装置(SUITE)和微振动隔离系统(MVIS)[2]。这些已有的系统只将Stewart 平台用于隔振，未有指向控制，而隔振指向一体化是未来发展的趋势[3]。目前也有许多振动控制系统被提出，既可保护敏感载荷免受振动干扰，又能提供指向功能。Zhang 提出压电陶瓷驱动的Stewart 平台用于卫星上[4]，指向精度高，但仅能隔离低频振动，隔振效果不佳；Washington 大学设计一种新的六自由度平台，使用音圈电机作为驱动器[5]，即可用作隔振也可用于太空系统的指向控制，但是跟踪精度不高；Wang 提出基于电磁电机的Stewart平台用于主动隔振系统中[6]。这些研究实现了隔振指向一体化，但都需要在二者之间找一定的平衡点。其本质原因在于隔振功能要求系统带宽低，而带宽低造成系统跟踪精度难以提高。总的来说，在有隔振功能的Stewart 平台上很难实现高精度跟踪。为了进一步解决Stewart 平台的隔振和跟踪之间不可调和的矛盾，已有很多学者提出双阶系统。相比于单阶系统，双阶系统有更好的隔振和跟踪性能。Kong 提出双级电机结构的Stewart 平台，即Stewart 平台的每个支柱用由音圈电机和压电陶瓷电机串联而成，但此结构设计复杂，目前仅处于仿真阶段；ACCESS 卫星上采用Tip-Tit Mirror(TTM)和Stewart 组成的双阶结构[7-8]，粗级子系统用于卸载精级子系统的位置值，并利用精级子系统的高精密控制进一步抑制跟踪误差，从而提高跟踪精度，但此系统中的粗级和精级各有一个光学探测器；Hai 等学者设计的粗级和精级输出直接相加的双阶结构[9]，但控制方式复杂。本文在基于位置输出的卸载方式的基础上进行改进，可避免设计解耦环节，降低工程上的应用难度。双阶系统主要依靠精级子系统的误差抑制能力以提高系统的跟踪精度，因此基于CCD 跟踪的TTM 闭环系统的控制器设计至关重要。目前已有通过多环控制、复合控制等方法以提高TTM 误差抑制能力[10-12]。但这些方法从系统结构上变得更加复杂，并且需要额外的硬件传感器，会带来更多的测量噪声。针对此问题，改进传统的PID 控制器，设计PI-PI 控制算法[13]，可有效提高系统在低频处的误差抑制能力。

通过引入双阶结构，以提高单阶Stewart 平台的跟踪精度，解决了隔振指向一体化系统中隔振性能和跟踪精度之间的矛盾。在仅有一个CCD 为系统提供图像信息时，传统的双阶结构很难设计解耦环节以保证稳定性，因此本文提出新结构的双阶控制，使得解耦环节变得容易实现。在不引入额外的硬件条件情况下，设计了PI-PI 控制器，以进一步提高系统跟踪精度。本文安排如下：第二节介绍双阶系统的性能分析；第三节介绍控制器设计；第四节介绍实验搭建及实验结果；第五节总结了理论分析以及实验结果并展望下一步工作。

2 双阶系统模型

本文提到的系统简图如图1 所示。光源用作模拟跟踪物，光路经过Stewart 平台以及平台上方的TTM共同矫正后到达CCD。CCD 作为系统种唯一的光学探测器，为系统控制器提供目标反馈信息。

图1 系统简图Fig.1 System schematic

为了能实现高精度跟踪，目前有效的控制方式就是设计多阶控制系统。多阶系统的整体思路是利用精度高但行程小的控制环去消减精度低但行程大的控制环的跟踪残差，以提高整体系统的跟踪精度。将Stewart 平台和TTM 结合以组成双阶系统，其中Stewart平台作为第一级(粗级)，TTM 作为第二级(精级)。传统的思路是将测量到的精级输出直接卸载至Stewart平台，其控制结构如图2 所示。

其中，e−τs表示电视的延时环节，Hs(s)表示卸载解耦环节。设MF(s)=CTTM(s)GTTM(s)，MC(s)=CSte(s)GSte(s)，考察图2 中系统闭环传递函数，如式(1)所示。

图2 传统的双阶控制系统Fig.2 Traditional two-stage control system

从式(1)可得，在满足Hs(s)=e−τs时，系统传递函数变为式(2)：

其中：[1+MF(s)]和[1+MC(s)]分别为精级和粗级闭环子系统特征方程，因此系统稳定必要条件是精级和粗级子系统的闭环传递函数无不稳定极点。此时，系统的误差抑制函数为

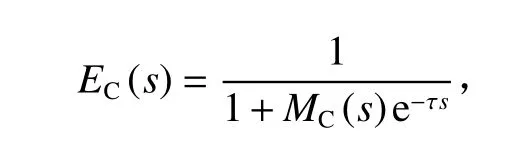
分别表示精级和粗级的误差抑制函数。从式(3)可知双阶系统的型别是粗级和精级系统的型别之和，因此双阶系统具有很高的控制精度。但此前提是要满足式(2)，那么就要求将Hs(s)设计成CCD 一样的传感器特性，这在实际中很难做到，会造成系统稳定性存在较大的不确定性。针对此问题，可对图1 的双阶结构进行改进，如图3 所示。

为了简化书写，设

则图3 中系统闭环传递函数表达式：

图3 改进后的双阶控制系统Fig.3 Improved two-stage control system

为精级子系统闭环传递函数。由于精级子系统带宽高于粗级子系统的带宽，因此可有GF(s)≈1。因此，只要有Hs(s)=1，即可使粗精子系统解耦。此时系统的误差抑制传递函数如式(5)：

由式(5)可知，在解耦情况下，新结构的误差抑制能力在带宽内和原结构等效。因此，则可根据精级和粗级的特点，独立设计控制器。

3 控制器设计

3.1 粗级系统控制器设计

Stewart 平台由基座、载荷平台和六个支杆组成，具有六自由度运动特性。粗级子系统中的控制对象便是Cubic 构型的Stewart 平台，Cubic 构型的Stewart平台的六个支杆之间的耦合程度最低，则可单独设计方位轴和俯仰轴的控制器，其闭环控制结构如图4 所示。

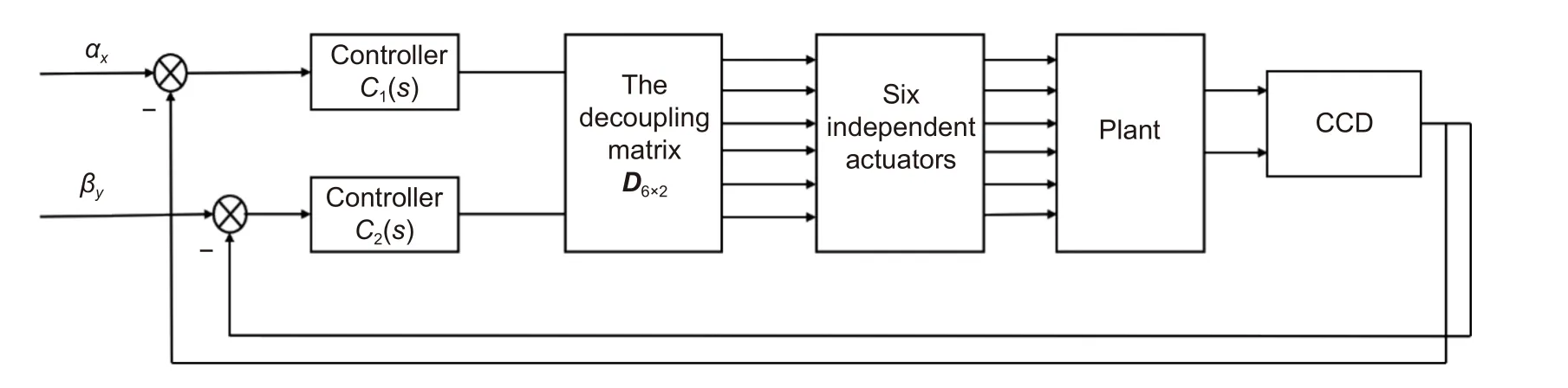
图4 粗级闭环系统Fig.4 Closed loop system of the coarse stage

由于本系统中Stewart 平台具有隔振功能其频率响应曲线如图5 所示，可将Stewart 平台看作一个低通滤波器。带宽为0.803 Hz，对象特性可写成

图5 Stewart 平台的频率响应曲线Fig.5 Frequency response curve of the Stewart platform

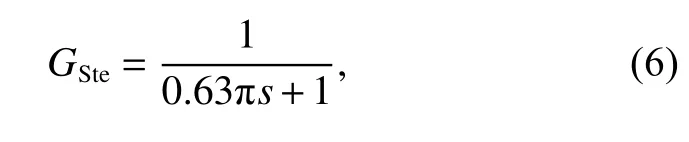
则精级系统开环传递函数为

由此可设计PI 控制器。

3.2 精级系统控制器设计

精级闭环系统如图6 所示。

图6 精级闭环系统Fig.6 Closed loop system of the fine stage

则精级系统开环传递函数为

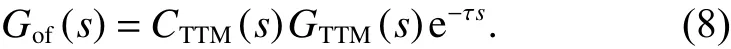
一般而言，TTM 的开环特性有很高的带宽，因此GTTM(s)=1。在TTM 的控制器设计中，为了不放大高频扰动而不设计微分环节，而只设计PI 控制器，即kp(kis+1)/s，这也降低了系统在低频处的控制精度。而在理想情况下，当设计的控制器是纯积分控制器时控制精度是最高的。此时控制器形式为C0(s)=k/s，其中k0是控制器待定增益值。根据相位稳定裕度PM≥π/4，则有：

其中：ωc0是此时的系统穿越频率。从式(9)可知，纯积分控制的参数整定仅和系统时延有关。

设计的控制器应该着重提高系统的低频误差抑制能力，将两个PI 控制器串联，组成PI-PI 控制器，即：

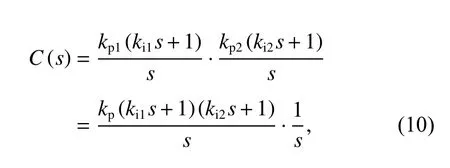
其中：kp=kp1kp2。从式(10)可看出，PI-PI 控制器也可是一个PID 控制器和纯积分环节串联。相对于通常的PI 控制器，弥补了没有微分器的缺点；而相对于普通的PID 控制器，PI-PI 控制器增加一个积分环节来抑制微分环节可能带来的高频扰动，因此PI-PI 控制器可提高低频处系统误差抑制能力。

根据相位裕度的定义，有：

为了提高低频处系统控制精度，可令ωc=ωc0，再将式(9)代入式(12)第一个方程可得：

将式(14)代入(12)中，进一步转化为优化问题：

分别使用积分控制器和PI-PI 控制器代替图4 中CTTM(s)，取延时环节τ=0.06 s 并仿真，得到系统误差抑制曲线如图7 所示。从图7 中可看出，在低频处PI-PI 控制器具有更高的误差抑制能力，符合系统需求。

图7 积分控制器和PI-PI 控制误差抑制曲线仿真图Fig.7 Integral controller and pi-pi control error suppression curve simulation diagram

4 实验验证

搭建实验验证上述理论的正确性，实验平台如图8 所示。其中CCD 和TTM 都置于Stewart 平台上，光路经过TTM 到达CCD。CCD 的数据信息经过图像处理单元处理后传至控制单元，控制单元主要由数字信号处理模块(DSP)、场可编程序门阵列(FPGA)、模数转化模块(A/D)、数模转化模块(D/A)和串口(UART)组成。误差信息经过DSP 处理后得到控制量，经过驱动放大后分别用于控制TTM 进而得到卸载量用以控制Stewart 平台。

图8 双阶系统实验图Fig.8 Experimental diagram of the two-stage system

CCD 的采样频率为50 Hz,分辨率为 1 k×1 k，像元尺寸为45 μm，焦距为500 mm；TTM 的驱动电机是压电陶瓷，精度为0.2′′，镜头的转动角度范围为∓160″；Stewart 平台的驱动电机为音圈电机，行程大，Stewart 平台的转动角度范围为∓0.886◦。

4.1 TTM 子系统控制实验结果

CCD 采样频率为50 Hz，且CCD 获得的图像需延时3 帧才可用于控制，则取τ=0.06 s。在低频处可将TTM 的对象特性看作是1。则根据理论分析分别设计PI 控制器和PI-PI 控制器。分别测量二者闭环控制时的误差抑制频响，如图9 所示。可见，在跟踪目标频率低于1 Hz，PI-PI 控制器的误差抑制能力要比PI 控制器强。

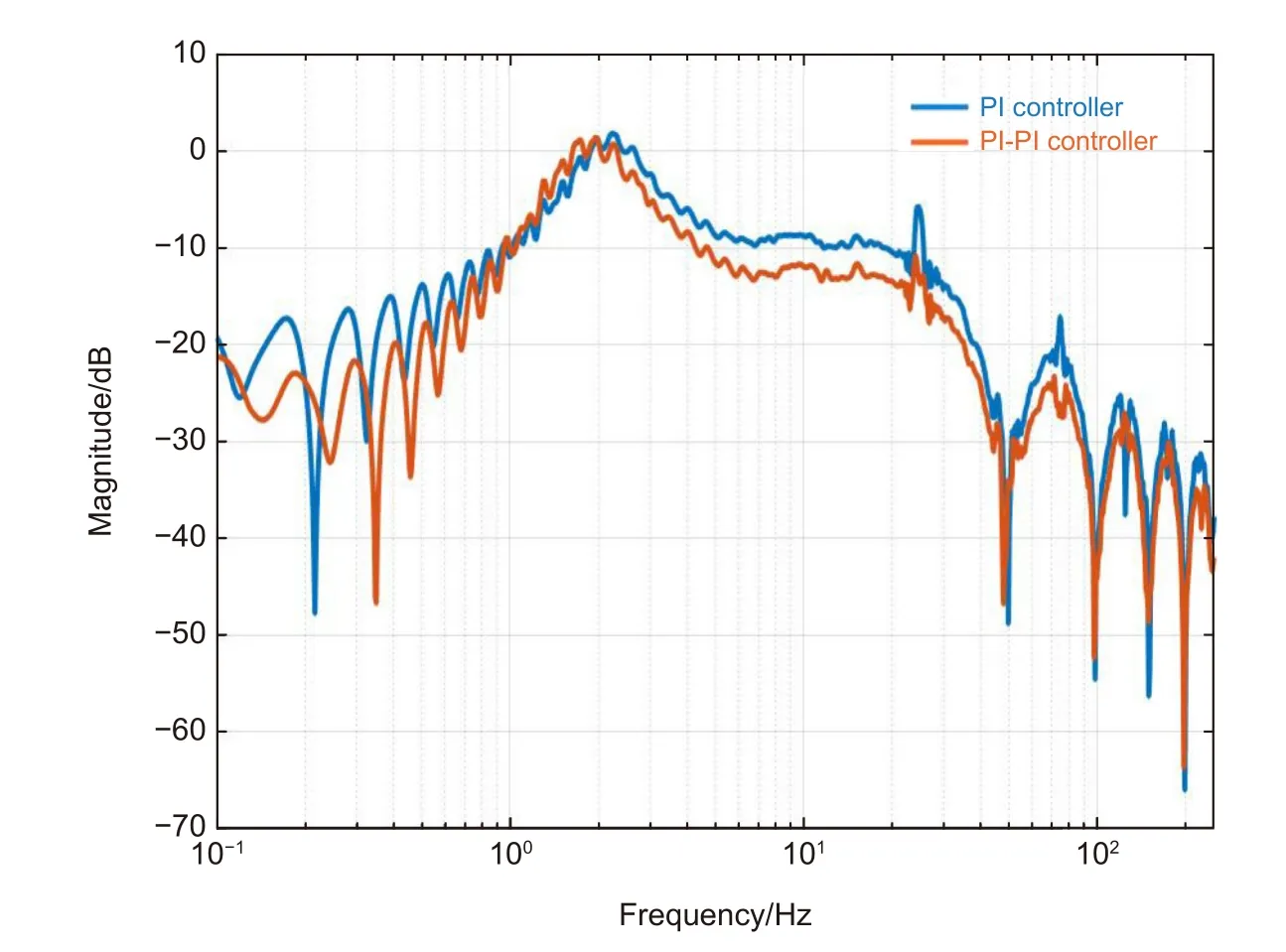
图9 PI 与PI-PI 控制器的误差抑制曲线对比Fig.9 The error suppression curve of the PI and PI-PI controller is compared

在模拟跟踪目标按以0.05 Hz 正弦运动，所得到的跟踪误差的时域及频域如图10(a)所示。从时域图中可见，PI-PI 控制器相对于PI 控制器跟踪精度有极大的提高。其中PI 控制的误差RMS 为21.89″，PI-PI控制误差的RMS为3.25″，降低了85.17%。从频域上可看出，PI-PI 控制器的引进在基频处的抑制能力提升显著，而不会再引入谐波干扰。而当目标以0.8 Hz正弦运动时(如图10(b))，PI-PI 控制效果并无明显提高，说明PI-PI 控制器在小于0.8 Hz 的低频处可有效提升控制精度，而在其他频段和PI 控制器效果类似。

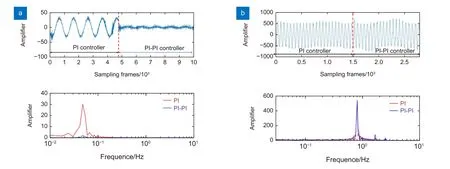
图10 双阶系统实验图。(a) f=0.05 Hz;(b) f=0.80 HzFig.10 The two-stage system experiment.(a) f=0.05 Hz;(b) f=0.80 Hz

4.2 双阶控制系统与单阶系统实验结果对比分析

双阶控制中卸载量是精级子系统的位置输出，通过应变片测量而得。由于应变片采样频率为2 kHz，基本可满足Hs(s)=1，系统解耦。卸载量变化过程如图10 所示。其中第一阶段系统定点指向，第二阶段系统跟踪正弦运动目标。应变片量程为∓16384，而卸载量在稳定状态不超过满量程的13%，说明精级系统中TTM 一直保持小角度的运动范围。

图11 双阶控制中卸载量变化过程Fig.11 The process of unloading quantization in two-stage control

模拟目标以0.01 Hz、0.02 Hz 和0.05 Hz 的正弦运动时，分别测得单阶结构和双阶结构的跟踪误差，如图12 所示，相应的误差RMS 对比如表1 所示。

从图12 和表1 可看出，相比于单阶结构，双阶结构有更好的误差抑制能力，验证了理论推导的正确性。实际上，正是由于卸载量很小，TTM 处于小角度运动，才使得系统精度有了质的提高。

表1 3 种频率下单阶结构和双阶结构的跟踪误差RMS 对比Table 1 RMS comparison of tracking errors between single-order structure and double-order structure at three frequencies

图12 单阶结构和双阶结构的跟踪误差对比。(a) 0.01 Hz；(b) 0.02 Hz；(c) 0.05 HzFig.12 The tracking error of single-order structure and two-step structure is compared.(a) 0.01 Hz；(b) 0.02 Hz；(c) 0.05 Hz

5 结论

本文针对Stewart 平台双阶控制系统，提出了基于精级位置输出的卸载控制。在理论上，新双阶结构相对于传统的双阶控制有等效的误差抑制能力；在工程上，新结构的解耦环节更容易实现，降低控制难度，并由此可单独设计粗精级子系统的控制器。对于粗级子系统，可将Stewart 平台看作是低通滤波器，设计普通PID 进行控制；而精级子系统是整体系统的跟踪精度提高的本质原因，因此设计PI-PI 控制器提高系统低频误差抑制能力。经过仿真和实验可得出PI-PI控制器相比于普通的PI 控制器在低频处有更强的误差抑制能力，同时不会引入高次谐波。设计单CCD的双阶控制实验，由实验结果可看出，双阶结构相比与仅用Stewart 平台可提升2～4 倍的误差抑制能力，较好地解决了用于隔振的Stewart 平台跟踪精度难以提高的问题。本研究中需要传感器测量精级子系统的位置输出用于卸载，而由于传感器采样频率高而近似满足系统解耦条件，同时传感器必然存在测量噪声，如何克服这些问题是下一步需要研究的工作。