基于实际工程的扶壁式排桩支护结构三维有限元模拟

罗雄章 广西建筑科学研究设计院

1 前言

随着城市建筑密度日益增加，周边建筑物对基坑土体的变形越来越敏感，与此同时，支护空间受到了很大限制。桩锚支护或单排桩加内支撑支护在控制基坑变形方面效果虽然较好，但桩锚结构受环境条件限制，内支撑结构占用空间大而影响后续施工。双排桩支护结构作为常用的深基坑支护方式，其弥补了桩锚支护或单排桩加内支撑的缺陷。双排桩支护体系由前、后排桩及连系梁构成一种门式刚架体系，与桩间土体协同工作以支挡基坑侧壁土压力。双排桩支护结构在受力之后，其自我调整与分配使得内力分布合理，且能有效控制基坑周边土体变形。但当基坑周边支护空间过窄时，出现了只有后排桩挡土，前排桩位于基坑内部的一种新型多排桩支护结构，许胜才等[1]将之称为特殊双排桩以区别于一般双排桩，并采用ABAQUS 有限元软件对其支护效应进行模拟分析。扶壁式排桩支护结构是在支护空间受限制的情况下提出的另一种新型多排桩支护形式，即在单排桩基础上每间隔两根支护桩设置三排桩作为扶壁支撑，排桩间通过刚架梁连接，只有后排桩支挡基坑侧壁，前排桩及中排桩置于地下室内侧，且排桩间土体被挖除，便于后期基础工程桩施工，连系梁穿过地下连续墙，待主体结构施工完毕，切除前、中排桩及连系梁。

2 双排桩或多排桩支护结构研究现状

本文主要借鉴学者们对于双排桩结构的研究成果，目前，双排桩的相关设计计算方法包括弹性抗力法[2]、极限平衡法[3]及数值计算法。刘泉声等基于弹性抗力法思想，建立平面杆系有限元模型，对双排桩结构的受力变形及相关影响参数进行了研究讨论，李俊丽等采用ABAQUS 有限元软件结合实际工程建立双排桩计算模型，分析研究开挖深度、排距、双排桩布置形式对双排桩受力及变形的影响。三排桩结构多被用于高深岸坡支护，田忠青等建立平面杆系有限元模型，通过对土压力分配与土弹簧的研究探讨，提出三排桩修正计算模型。

目前，针对双排桩或者三排桩结构的研究存在以下问题。（1）基于极限平衡法或者弹性抗力法进行双排桩支护结构模拟分析，不可避免前后排桩的土压力分配问题；（2）基于Winkler地基梁思想建立的双排桩或三排桩平面杆系模型，把基坑开挖看作平面问题，且把桩简化成梁单元的过程中，忽略了桩土摩擦作用；（3）针对三排桩的数值模拟文献不多，且是针对桩排间有土体的。桩排间无土体的扶壁式排桩支护效应研究缺乏文献资料，本文在总结、借鉴双排桩或三排桩研究资料的基础上，基于实际工程，对桩排间无土体的扶壁式排桩这一新型支护结构进行有限元模拟分析，并与双排桩支护结构进行比较，为扶壁式排桩支护结构在实际工程设计上的应用提供参考。

3 工程实例

3.1 工程概况

某新建路北侧有一在建商住楼项目，规划用地内包括4栋31～32层高层住宅楼，设2层整体地下室，地下室东面、南面距市政道路边5m～7m，北面开阔，西面3m 处为一栋4 层高移动通信生产综合楼，楼内安装的生产设备对变形非常敏感。同时，地下室西侧有设备管线、自来水管等地下管道，位置不详。

依据岩土工程勘察报告及土工试验成果，对场地地质情况进行适当简化后，场地土层和排桩的物理力学参数见表1所示。场地内分布一层地下水，属孔隙潜水，主要赋存于各土层的孔隙及裂隙中，水量不大。水位埋深稳定在4.60m～8.30m，受大气降水及周围生活用水补给。为反映基坑周边建筑物对基坑开挖的影响，在基坑周边地面按每层楼10kPa施加局部荷载。

表1 各土层及桩体物理力学参数

该建筑基坑支护工程平面尺寸为145m×115m，周长为520m，基坑开挖深度约为7.0m，属深大基坑，为保证基坑稳定需进行支护。考虑到基坑西面周边环境对基坑土体变形控制的要求较高，但建筑红线内可利用空间非常有限，限制了双排桩支护的使用，所以在基坑西侧采用扶壁式排桩支护形式。如图1所示，后排桩的布置采用密排形式，前、中排桩则每间隔两根后排桩进行布置，设计排桩排间距分别为2.0m、2.55m，桩间距为2.0m，设计桩径1.2m，排桩间刚架梁宽1500mm、高1000mm。

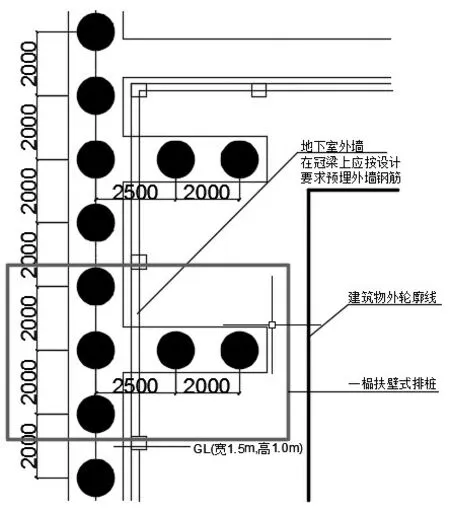
图1 扶壁式排桩平面布置图

3.2 基本假定和有限元设置

为简化计算，采用总应力法，且不考虑地下水作用及支护结构施工对土体的扰动。假设桩土间的相互作用方式为表面与表面接触，将接触面定义为基于Coulomb 摩擦定律的硬接触且摩擦公式为“罚”。有限元软件计算生成的地应力需符合半无限空间体自重应力的分布规律，因此，在ABAQUS 三维模型的地应力分析步中，将边界条件设置为周围只约束水平位移，底部施加三个方向的全部约束。在网格划分时，为有效模拟土体变形，将其定义为C3D8R减缩积分单元，桩体和连系梁则选择C3D8I 非协调单元，以更好反映桩体和连系梁的弯曲变形。土体材料本构关系选择应用广泛的Mohr-Coulomb理想弹塑性模型，它既能反映岩土材料拉压强度不同的SD效应，又能反映对静水压力的敏感性。桩体及刚架梁采用线弹性模型，无需考虑混凝土的屈服效应。

3.3 施加初始应力场的方法

实际工程中，可认为在基坑开挖前，土体应力存在，但地表位移为零，这种有应力无位移的时间点称作地应力平衡。

采用有限元软件进行岩土工程数值模拟时，初始地应力是必须考虑的重要因素，初始地应力平衡是确保数值计算结果正确性的关键，初始地应力平衡需满足两个条件：（1）平衡条件——由应力场形成的结点荷载要和所施加的外荷载平衡；（2）屈服条件——所有点的应力不能位于屈服面外。

采用ABAQUS 可以很好地实现这个功能。首先建立地应力平衡分析步，对整个模型施加重力荷载。一般情况下，定义的初始应力场与施加的重力荷载很难获得平衡，计算模型中，土体产生位移且不可忽略。所以先通过有限元软件算出各单元结点的应力值，再以inp 文件方式直接输入，步骤如下。（1）计算并输出结果。模型计算完成后，选择Report-Field output，在Variables选项下的Position选中Centroid，本文为三维模型，故应力变量选择S11，S22，S33，S12，S13，S23；在Setup 选项卡中将输出文件改为x.inp 格式，不勾选“附加到文件中”选项，并在Data选项中勾选Field output 即可。输出当前计算结果，即施加重力荷载形成的初始应力场。（2）修改结果。在Excel表格中导入结果文件x.inp，除数字结果外删除其他内容。注意将修改后的结果保存为x.csv格式，并与cae文件保存在同一文件夹中。（3）写入关键语句，重新进行计算。在Model 中选择Key word，打开初始inp文件，将“*initial conditions,type=stress,input=x.csv”语句写入其中，位置在“BOUNDARY CONDITIONS”之后，“，“STEP”之前。需注意，在导入上步结果文件的同时，在地应力平衡分析步中仍需施加重力荷载，使得各结点位移为零，达到初始地应力平衡状态。否则会产生与导入应力场方向相反的应力场，导致总应力为零，同时土体变形由压缩变为膨胀，与实际工程情况不符，具体计算分析详见文献[1]。

3.4 建立有限元模型

若建立完整模型，则划分的单元数目过大，所以需对计算模型进行简化。由于基坑西侧采用的扶壁式排桩支护结构，为本文的研究重点，所以模型中忽略其他不同型式的支护结构。为充分反映扶壁式排桩的支护效应，故选择如图1所示的一榀扶壁式排桩作为计算模型。考虑到基坑影响范围取基坑深度的4倍，竖向取30m，水平向取50m。

为比较分析扶壁式排桩与双排桩的内力分布及变形特征，利用等代刚度的概念，把扶壁式排桩体系等效代换为桩径1.26m，桩间距2.0m，排间距为2.55m的双排桩体系。等代刚度的设计理念及具体的计算方法见文献。

为模拟基坑开挖的施工过程，采用ABAQUS 中的生死单元功能。实现生死单元功能的具体操作分为三步。首先，地应力平衡分析步之后建立开挖分析步，根据基坑设计深度，对待开挖土体建立相应的几何集。之后，在开挖分析步中移除相应接触对。最后，通过inp 输入文件定义，写入位置在开挖分析步“END STEP”之前。建模过程中需重视：（1）由于网格生成的质量直接影响数值计算结果的精确性，所以在划分网格前，对计算模型进行必要切割，尤其桩身及其周边土体为复杂实体，需切割成精细规则的几何体以获得较好的网格质量。（2）桩土接触对应一个面对一个面逐一建立，否则容易导致数值计算不收敛。

3.5 计算结果分析

计算完成后，创建路径并输出实体单元的内力及变形成果表，进而得到扶壁式排桩的弯矩结果如图2所示，桩身变形如图3所示。

由图2和图3可知，后排桩的最大弯矩值位于桩深5m左右处，前排桩和中排桩的最大弯矩值位于桩深1m左右处且二者内力分布基本一致，前排桩和中排桩的最大弯矩值明显大于后排桩。前排桩和中排桩的水平位移最大值位于桩顶附近且二者变形挠曲度基本一致，而后排桩的水平位移最大值位于桩深4m左右处。图2、图3中可以看出后排桩的应力分布及变形曲线挠曲程度较前、中排桩偏大，因为扶壁式排桩支护体系中只有后排桩直接承受土压力作用，而前、中排桩类似于扶壁支撑。依据对前、中、后排桩桩身内力及变形分布特征的分析比较可知：在进行结构设计时，前排桩和中排桩的配筋应基本一致；加大桩身最大弯矩处的配筋，有针对性地提高桩身局部强度。

图2 扶壁式排桩桩身弯矩

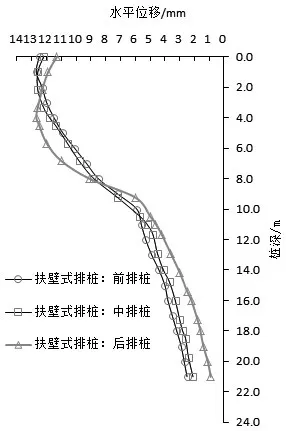
图3 扶壁式排桩桩身变形

为了比较扶壁式排桩与双排桩支护基坑开挖时的受力性状和变形规律，本文做了双排桩前后排桩间土体未开挖的工况模拟，可知双排桩的前排桩身弯矩最大值位于桩深5m左右处，后排桩弯矩最大值位于桩深1m左右处，双排桩的前后排桩变形曲线基本一致。

综合以上分析，相同条件下，双排桩的内力及变形较小，桩土协同作用明显，支护效果优于扶壁式排桩。但扶壁式排桩是针对支护空间过于狭窄的情况下提出的基坑支护结构形式，不拘泥于传统双排桩支护体系，具有良好支护效果。

按照有关技术规范，为保证基坑施工期间基坑支护边坡及周边建筑物的安全，同时为检验扶壁式排桩支护结构的支护效果，在其上布置3个水平位移观测点，桩顶最大水平位移监测值为9.4mm，与变形计算值11.3mm十分接近。

4 结束语

基于实际工程进行模拟分析，得出以下结论。

（1）有别于桩土协同作用的传统双排桩支护结构，扶壁式排桩的桩排间无土体，只有后排桩支撑挡土，这类支护结构不再受限于基坑周边的支护空间。（2）通过桩身内力分布图得出，扶壁式排桩弯矩最大值出现在前中排桩近桩顶刚结点处，双排桩弯矩最大值位于桩体中上部。综合分析比较内力和变形结果，双排桩支护效果优于扶壁式排桩。（3）三维有限元模型计算结果反映了支护结构的内力分布及变形特征，设计时可针对性地对支护结构进行优化。（4）扶壁式结构已经应用于实际工程中，从监测结果来看，支护效果良好。