灰色关联与麻雀优化算法预测光伏发电量研究

成 珂，张 璐，杨力人，劳志军

(1.西北工业大学动力与能源学院，陕西西安 710072；2.西安博威新能源科技有限公司，陕西西安 710000)

由于外界环境变化，光伏发电存在波动性与间歇性，并入电网后会对电力系统的运行产生影响。准确地对发电量进行预测，有助于电力调度部门提前做好安排，降低对电网的冲击。多数学者针对光伏发电量预测进行了相应研究，选择出相关性最大的因素及合适的预测模型是提高预测精度的关键。

关于光伏发电的影响因素，何旻[1]针对影响光伏发电的主要因素提取不当及数据质量不高的问题，提出了基于copula 函数的相关性分析方法。Long Huan 等[2]提出一种参数选择方法用于选择光伏预测的重要参数。Khan Idris 等[3]基于雾霾特殊天气下光伏预测精度低的情况，引入空气质量指数(AQI)及温度、风速、湿度等常规参数作为预测模型的输入量。陆爽等[4]基于Pearson 相关系数分析辐照强度、气温等与光伏发电量的相关性。

同时需建立合适的预测模型，目前在光伏发电量预测中应用较多的有马尔科夫链、支持向量机、人工神经网络等[5]。Sharadga Hussein 等[6]对比了不同的时间序列预测方法，结果表明神经网络用于光伏发电量的预测比统计模型更准确。Gao Yang 等[7]依据历史光伏出力数据提出一种基于机器学习的自适应超短期直接预测模型。王晨阳等[8]提出利用遗传算法对卷积长短记忆混合神经网络模型(CNN-LSTM)参数进行优化，在预测精度及运行时间方面表现良好。

近年来城乡建筑屋顶建设的小型分布式光伏电站，一般不收集气象数据，采用上述方法预测较困难。因此本文利用公开的天气资料，依据8.16 kW 屋顶光伏电站2016―2021 年1 744 d 的实际运行数据，开展光伏发电量预测研究。研究首先基于聚类划分天气数据，采用灰色关联法分析各气象因素与光伏发电量之间的相关性，接着采用麻雀搜索算法优化预测模型，并与常规及采用粒子群优化的模型进行了对比。

1 研究理论

1.1 气象因素优化

不同天气类型下的太阳辐射、温度等气象因素有不一样的规律变化，导致光伏发电存在较大的差异。相关性分析方法对气象因素进行筛选，可以提高不同天气类型的预测精度。其中灰色关联度是一种多因素分析方法，通过计算能得到某个量受其他因素影响相对强弱，可获得多个不同因素之间的关联程度。由于对样本数量要求不高、计算量小等特点[9]，故本文选择灰色关联分析作为筛选气象因素的方法，得到研究对象与各影响因素之间的关联度后，通过比较各个关联度的大小对二者的关联程度进行分析，进而得到与研究对象关联性较大的因素。

1.2 预测算法优化

光伏发电量预测常采用误差反向传播神经网络(error back propagation neural network，BP)，即通过梯度下降法将误差反向传播更新权重w和偏差b完成训练进而进行预测，是目前预测技术中有效的神经网络算法之一。本文选择典型的3 层神经元网络结构，通过对数据的处理，确定以西安马王镇2016―2021 年的有效数据作为研究样本，其中输入量为2016―2021 年对应的温度、相对湿度等气象因素，输出量为采集的日发电量数据。

三层的BP 网络应用广泛，但因其收敛速度慢、易陷入局部极值等缺点，需要对BP 网络进行改进。常见的群智能优化算法有遗传算法、粒子群算法、蝙蝠算法及灰狼算法等，因其在适用性、收敛性及稳定性等方面的优势，在组合算法中应用较广泛。本文基于天气聚类及灰色关联的结果，采用麻雀搜索算法(sparrow search algorithm，SSA)优化BP 预测模型的权重及偏差值，实现提高预测精度的目的，并与常规及采用粒子群优化算法(partical swarm optimization，PSOBP)的模型进行了对比。

1.2.1 麻雀优化模型

麻雀搜索算法是Xue 等[10]依据麻雀觅食行为及反捕食行为提出的一种群体优化算法，具有搜索能力强且调节参数少的优点。算法本身依托于麻雀的生物行为，麻雀种群中具有较高适应度、能够提供觅食区域及方向的是发现者；跟随发现者能够搜索到食物丰富的区域的是加入者；同时部分加入者为增加捕食率会监视发现者并抢夺食物；当监测到捕食者时，通过鸣叫报警引导加入者进入安全区域。其流程图及优化过程如图1 所示。

图1 麻雀搜索及优化算法流程图

麻雀搜索优化算法首先确定BP 及麻雀网络结构及参数，通过计算初始种群适应度值并进行排序，对发现者、加入者及预警者的位置进行更新，得到当前最优解。通过对比判断是否满足更新操作的要求，得到全局最优解并传递给BP 网络进行优化。

其发现者位置更新公式为：

式中：Xij为第i只麻雀在第j维中的位置，j=1,2,3...d；t为迭代次数；maxiter为最大迭代次数；α∈(0,1]的随机数；Q为服从正态分布的随机数；L为1×d的矩阵，矩阵内全部元素均为1；R2∈[0,1]为预警值；ST∈[0.5,1]为安全值。

加入者位置更新公式为：

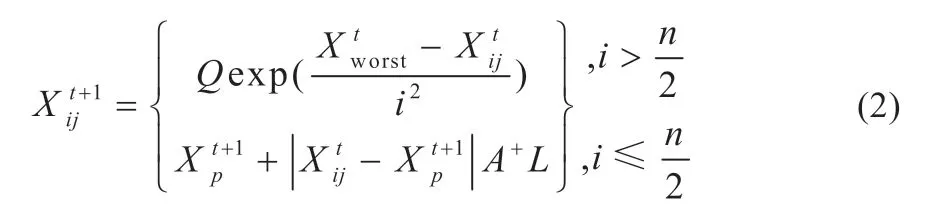
式中：Xp为当前发现者占据的最优位置；Xworst为当前全局最差位置；A为1×d的矩阵，矩阵内的元素随机赋值为1 或－1。

预警者位置更新公式为：

式中：Xbest为当前全局最优位置；b为步长控制参数，值为服从均值为0、方差为1 的正态分布随机数；K为[－1,1]之间的随机数；fi为第i只麻雀的适应度值；fg为当前全局最优适应度值；fw为当前全局最差适应度值。

1.2.2 粒子群优化模型

PSO 是一种群体智能优化算法，通过各粒子之间的相互作用，对特定的区域进行智能搜索。基本思想是初始化一群包含BP 网络权值及偏差的粒子，并用位置、速度及适应度来表征粒子属性，通过跟踪个体最佳位置及群体最佳位置得到BP 网络最佳的初始化权值及偏差值，达到优化的目的，具体流程如图2 所示。

图2 PSO-BP算法流程图

2 小型光伏电站

研究以陕西省西安市马王镇小型光伏电站为例，采用2016―2021 年的光伏发电量实际运行数据，以及对应时间序列的公开气象数据。该电站处于北纬34.194°，东经108.707°，属太阳能资源III 类地区，年总辐射量45.74×108MJ/m2，平均每天约有5.43～6.21 h 的日照，全年约有1 983.4～2 267.3 h 的日照时长。图3 为光伏电站。

图3 光伏电站

该电站为建筑屋顶安装的分布式小型光伏电站，装机容量为8.16 kW。光伏组件正南方向排列，安装倾角为23°。光伏组件选型为HH255(30)P，单个容量为255 W，单块尺寸1 650 mm×992 mm×40 mm，工作电压为30.10 V，工作电流8.47 A，组件效率15.67%，方阵排列方式为16 块串联为一个单元，2 个单元并联。并网逆变器型号为suntree8000TL，数量1 台，最大直流(DC)输入电压9 000 V，最大效率98%，三相输出，具有防孤岛、过欠电压关机等功能。

3 研究过程

3.1 数据处理

整理电站记录的数据得到光伏发电数据1 789 d，为提高数据的可靠性，将整理的数据进行初步清洗，结果表明缺失及无效值有7 d，由于数据较少，直接简单筛除，故得到有效的光伏发电及气象数据1 782 d。接着以辐射量与发电量作为筛选参数，二者拟合后选择95%置信将远离样本主体的离群值剔除，得到1 744 d 有效数据，具体如图4 所示。

图4 剔除离群值

3.2 天气聚类

5 年的数据中包含不同的天气类型，从数据中选取连续一周的光伏输出功率数据，曲线变化如图5 所示，明显可见不同天气下的光伏发电有较大差异。为减少类型数对预测精度的影响，需要对天气类型进行分类处理。

图5 不同天气下光伏输出功率曲线

分类过多时，预测需要大量的数据样本；分类过少时，每一类天气类型复杂导致预测精度低。因此本文基于初次划分的天气类型利用SPSS 进行二次聚类划分，具体如图6 所示。根据聚类结果，将复杂的天气类型进行分类合并，考虑到样本数据有限，当分类数过多可能对预测精度产生的影响，本文选择相对距离为3.5 将其分为6 类，其中A 类样本330，B 类样本299，C 类样本588，D 类样本269，E 类样本179，F 类样本79。

图6 使用平均联接(组间)的谱系图

3.3 灰色关联度分析

基于1.1 节的内容，本文选择太阳辐射、晴空指数及相对湿度等10 个参数作为灰色关联度计算的比较序列，实际光伏发电量作为参考序列。以A 类样本为例，根据计算得到各个气象因子与光伏发电量的相关度如表1 所示。

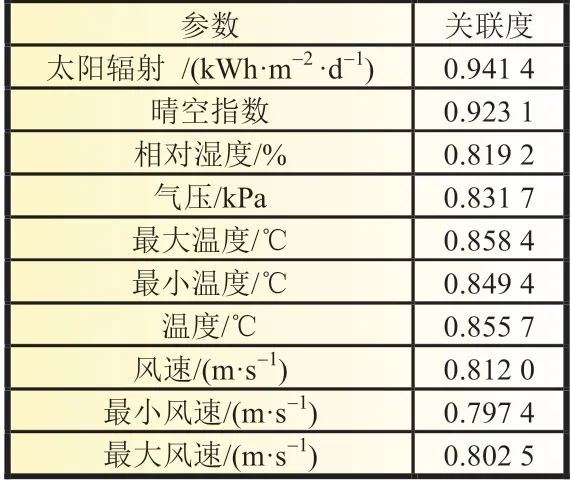
表1 A 类灰色关联度

结果表明，选取的各气象因素的灰色关联度均大于0.6，表明各气象因子与发电量之间有一定的关联性，A 类样本选择太阳辐射、晴空指数等大于0.8 的9 个参数作为输入特征进行发电量预测。同理B-F 类样本取10、9、8、8 及9 个参数依次作为输入量。

3.4 预测模型实现

借助MATLAB 平台，结合1.2 及3.3 节的内容，确定预测模型的输入量为温度、相对湿度等各种气象因素，但由于包含不同天气类型的研究样本基于灰色关联分析导致A、B 及C等6 类样本的输入量有差异，输出量为电站实际的光伏发电量，隐含层节点数采用经验公式来确定。

为与粒子群优化算法进行对比，麻雀优化算法与粒子群优化参数设置保持一致，种群数为20，最大迭代数为100，依据各分类样本下的输入量及隐含层个数，得到种群维度为M=输入层神经元数×隐含层神经元数+隐含层神经元数×输出层神经元数+隐含层神经元数+输出层神经元数，随机生成M个包含神经网络权值及偏差信息的粒子，通过迭代寻优将最优的权值及偏差值赋给BP 网络，进行后续训练预测。

4 研究结果与分析

4.1 评价指标

为准确评价预测模型的性能，本文选择了平均绝对误差(MAE)、平均平方根误差(RMSE)及平均绝对百分比误差(MAPE)三个参数作为评价指标，其中ti为预测值，yi为实际值，n为样本数。具体的计算方法如下：

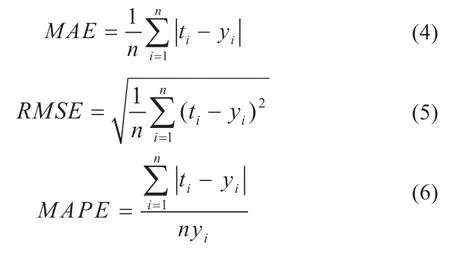
4.2 预测结果及分析

结合3.2～3.4 节的内容，将经过灰色关联筛选后的数据分别基于天气聚类输入到BP、粒子群优化BP(PSOBP)及麻雀优化BP(SSABP)模型中进行分析。具体结果如图7 所示。

图7 所示依次为A-F 等6 类天气下的预测结果对比，A、B、D 及E 类的曲线更贴近真实曲线；而C 及F 类天气下受到云层、雨水等的影响较大，复杂的天气变化情况使光伏发电波动性更强，导致预测误差较大。

根据表2 进一步对预测结果进行分析，从各项评价指标可见优化后的算法比BP 算法性能更好，且麻雀优化算法比粒子群优化算法预测误差更小。如A 类天气下相比常规BP 预测，PSOBP 预测平均绝对误差可降低0.131 4 kWh，平均平方根误差可降低0.115 8 kWh，平均绝对百分比误差可降低0.120 4。SSABP 预测平均绝对误差可降低0.303 1 kWh，平均平方根误差可降低0.345 6 kWh，平均绝对百分比误差可降低0.133 0。通过比较，SSABP 比常规方法平均绝对误差可降低0.419 7 kWh，平均平方根误差可降低0.412 6 kWh，平均绝对百分比误差可降低0.082 9；比PSOBP 平均绝对误差可降低0.209 8 kWh，平均平方根误差可降低0.235 5 kWh，平均绝对百分比误差可降低0.052 5。

表2 预测结果评价

5 结论

本文以实际小型光伏电站为研究对象，为提高不同天气类型下的预测精度，基于聚类划分天气数据，并采用灰色关联法分析气象因素与光伏发电量之间的相关性，结合优化算法实现了日光伏发电量预测。结果表明：

(1)对天气类型进行统计、划分得到6 类不同的子天气样本，为降低因输入量冗余度较大导致预测精度低的不利影响，每一类采用灰色关联法筛选出与发电量关联性较大的气象因素，划分的A、B 及C 等6 类样本下模型的输入量个数依次为9、10、9、8、8 及9。

(2)基于上述的结果，采用麻雀搜索算法优化BP 网络的权值及偏差值，并建立了BP、粒子群优化BP(PSOBP)及麻雀优化BP(SSABP)预测模型。

(3)每一类样本分别采用三种算法进行预测对比，预测结果可知优化后的算法预测精度更高，相比传统及粒子群优化算法，麻雀优化算法误差更小。

以上研究结果可为电力能源规划及可行性分析等提供支持，对于提高电网接纳光伏及电力系统的安全稳定运行有实际作用。本文将出现次数较少的天气归类到相近的天气类型中，对预测精度的提高有一定的影响，后续在增加样本的前提下，可细分天气类型，进一步提高预测精度。