压缩感知观测信号的低秩稀疏分解
潘金凤,尹丽菊,高明亮,邹国峰
(山东理工大学电气与电子工程学院,山东 淄博 255000)
0 概述
视频等具有背景缓慢变化及前景快速移动特点的信号被称为时变稀疏信号[1]。时变稀疏信号分析常需要的前景与背景的分离可用低秩稀疏分解实现。文献[2]提出基于主成分分析(Principal Component Analysis,PCA)的低秩稀疏分解方法,该方法分别使用稀疏、低秩矩阵作为前景与背景的数学模型,对低秩矩阵的估计使用基于PCA 的阈值法,其缺点是分解准确度在很大程度上依赖于初始值的设置,且移动前景被误归为低秩背景的概率较大。为了得到更准确的低秩稀疏分解结果,文献[3]介绍了使用目标特征域字典的基于PCA 的目标跟踪方法。文献[4-6]介绍了先将整个信号投影到其低秩背景的正交空间,再应用最小二乘法对信号的稀疏前景进行估计的方法。
压缩感知(Compressive Sensing,CS)信号处理方法能够在低于Nyquist 采样率的条件下实现信号的精确或近似精确重构,所以该理论下的采样与重构成为一个重要研究方向,在很多有关图像与视频处理的领域都得到应用。文献[7]提出了噪声服从高斯分布假设下的Bayesian 压缩感知重构方法。文献[8]将压缩感知技术应用于光学相干断层扫描成像数据的重构。文献[9-12]分别介绍了多光谱、近红外、并行以及三维压缩感知成像系统的实现方法。
时变稀疏信号压缩观测的重构方法大多基于其背景缓变、前景快变的特点。文献[13]介绍了使用张量的块压缩感知重构方法。文献[14]提出使用张量的SAR 图像的压缩感知重构方法。文献[15]提出在背景缓变假设下的卡尔曼滤波压缩感知重构方法。文献[16]根据各帧图像之间动态变化的特点,应用动态方程来实现动态压缩感知重构。以上方法都利用低秩与稀疏先验知识进行压缩感知重建,但没能分别给出低秩与稀疏部分的重构结果。由于动态压缩感知重构不能实现信号低秩与稀疏部分的直接分离重构,研究人员开始研究能够对两者直接分离的重构方法。文献[17]应用基于PCA 的低秩稀疏分解方法对高光谱图像进行压缩感知重构,其低秩部分的重构利用了多光谱图像的谱间低秩性与谱内稀疏性。文献[18]利用PCA 方法与文献[19]改进的正交匹配追踪方法,在假设视频低秩部分的秩与稀疏前景的稀疏度都已知的条件下,先估计低秩矩阵与稀疏矩阵的支撑集,再应用最小二乘方法实现时变稀疏信号的压缩观测的低秩稀疏分解(SpaRcs)。文献[20]利用移动的稀疏前景使视频各帧图像构成的二维矩阵呈现纹理特征的特点,改进了SpaRcs 方法的稀疏前景支撑集的估计方法。SpaRcs 及其改进方法更适用于静态低秩背景,但是对于缓变背景,其运行结果较差。
为提高信号压缩观测的低秩稀疏分解的准确度,本文基于文献[5]方法,提出两种不同稀疏前景压缩观测近似值的估计方法。首先将时变稀疏信号的压缩观测值投影到其低秩背景的正交空间,或将原信号投影到其低秩背景的正交空间后再压缩观测,再分别对稀疏前景及低秩背景进行压缩感知重构。
1 时变稀疏信号的压缩观测与正交投影
假设时变稀疏信号由T帧连续图像构成:

其中:X∊Rn×T;L与S分别是X的低秩与稀疏部分。
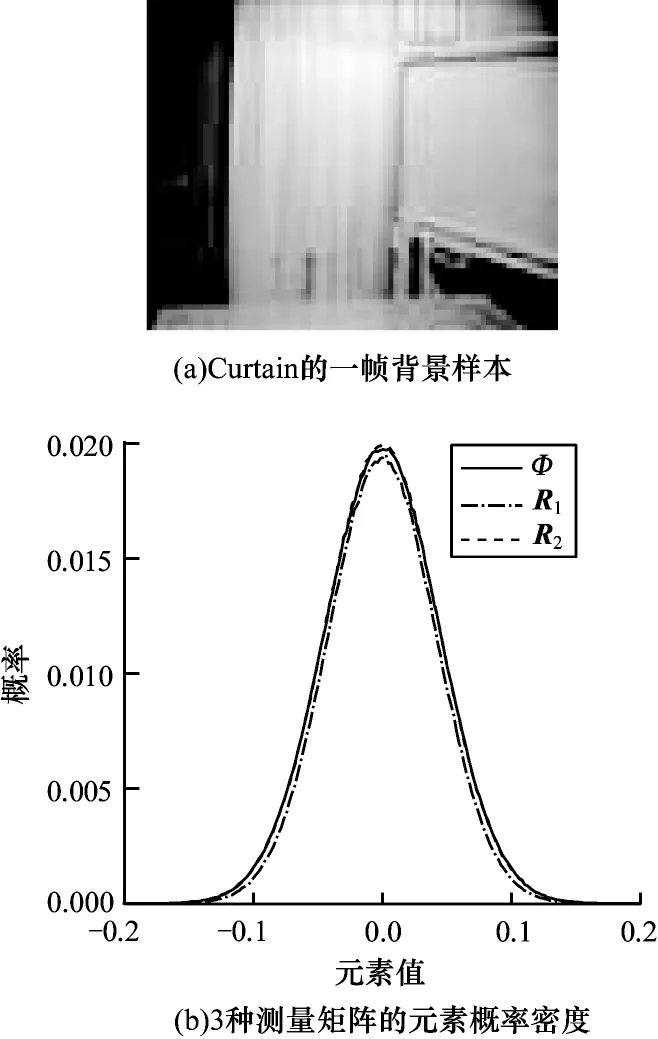
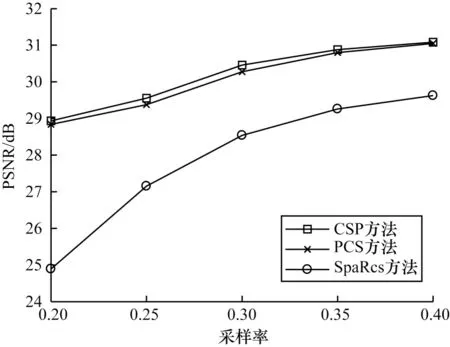
假设在对X进行压缩观测时,各帧图像都使用相同的 测量矩 阵Φ∊Rm×n(m< 对xt进行压缩观测,再投影到它的低秩背景压缩观测值的近似正交空间的过程可表示为: 其中:αt=PΦlt表示未能将Φlt准确投影到其正交空间形成的微小误差。若R1=PΦ符合测量矩阵的等距约束条件,则式(4)的压缩观测过程可以直接使用R1作为测量矩阵。 第2 种方法是先投影再压缩观测(CSP),该方法首先将信号X投影到它的低秩背景估计值的近似正交空间,然后再对该投影值进行压缩观测。因此,应先计算的奇异值分解并估计其支撑集矩阵的近似值UL和近似正交投影矩阵PL。将xt投影到它的低秩背景的近似正交空间,再进行压缩观测的过程可表示为: 其中:βt=ΦPLlt,PLlt表示未能完全将lt投影到其正交空间形成的微小误差。因为Φ是单位行向量测量矩阵,所以βt的各个元素也是微小值。若R2=ΦPL符合压缩感知测量矩阵的等距约束条件,则对xt的压缩观测也可以直接使用R2作为测量矩阵。 本文中Φ使用各元素服从N(0,1)分布的高斯测量矩阵,如果R1、R2同样是高斯矩阵,那么其性质与高斯测量矩阵相同,符合压缩感知信号处理对测量矩阵的要求,此时式(4)、式(5)中st的求解属于压缩感知重构问题。实验发现,若支撑集矩阵U1或UL由包含Φ或的部分能量的若干个较大非零奇异值对应的左奇异向量构成,则R1、R2的分布曲线平滑且基本与Φ服从相同的分布。图1(a)为Curtain 视频的一帧背景训练样本。图1(b)为对Curtain 的背景训练样本集,当压缩采样率为0.1 时,由保留95%能量的支撑集矩阵求得的R1、R2与高斯测量矩阵Φ的分布进行比较。如图1(b)所示,R1与Φ的分布差别稍大,R2与Φ的分布基本无差别,三者的分布差别非常小,所以R1、R2近似服从与Φ相同的高斯分布,可以作为测量矩阵使用。 图1 3 种测量矩阵元素的概率密度比较Fig.1 The comparison of probability density of three measurement matrice elements 将式(4)与式(5)表示的两种不同的压缩观测与投影过程统一表示为: 式(6)中st的求解可用基追踪去噪法,即: 求得st的估计值后,lt的估计也成为压缩感知重构问题: 应用基追踪算法即可求解lt的估计值。 时变稀疏信号压缩观测的低秩稀疏分解需要解决的另一问题是由信号低秩背景缓慢变化引起的。无论是先压缩观测再正交投影,还是先投影再压缩观测,当低秩背景产生变化时,它的正交投影矩阵就会改变,因而Θt也随之变化,因此需要解决如何判断低秩矩阵lt是否发生变化,及其变化是否导致了正交投影矩阵的较大变化问题。本文采用计算相邻帧低秩矩阵的结构相似度(Structural Similarity,SSIM)的方法来进行判断,若两者的SSIM 值小于阈值,说明低秩背景已经发生较大变化,需要重新计算正交投影矩阵。 应用第1 种先压缩观测再投影方法的时变稀疏信号压缩观测的低秩稀疏分解算法的实现步骤如算法1 所示。 算法1PCS算法 步骤1已知低秩背景训练样本,初始化高斯测量矩阵Φ∊Rm×n,参数c、η、th及t=1。 步骤2对低秩背景训练样本进行压缩观测得,然后估计保持其部分能量c的近似支撑集矩阵U1及正交投影矩阵P。 步骤3令测量矩阵Θt=PΦ,根据式(6)对时变稀疏信号xt进行压缩观测。 步骤4应用基追踪去噪算法与基追踪算法先后对稀疏信号st和低秩信号lt进行压缩感知重构。 步骤5t=t+1,若t>η且lt与lt-1的结构相似度SSIM 第2 种压缩观测方法是根据背景的训练样本,先将时变稀疏信号近似投影到它的低秩部分的正交空间,再对信号投影值进行压缩观测,两种方法的第4 步、第5 步相同,其前3 步的步骤如算法2所示。 算法2CPS算法 步骤1已知低秩背景训练样本初始化高斯测量矩阵Φ∊Rm×n,参数c,η,th及t=1。 步骤2计算保持低秩背景训练样本部分能量c所对应的近似支撑集矩阵UL及其正交投影矩阵PL。 步骤3令测量矩阵Θt=ΦPL,根据式(6)对时变稀疏信号xt进行压缩观测。 SpaRcs 是一种能够根据压缩观测值直接实现信号的前景、背景分离的重构方法。所以,实验时将SpaRcs 方法与本文的PCS 方法、CSP 方法进行比较。 图2 是压缩观测采样率m/n=0.3 时,3 种方法对Curtain 视频的压缩观测的低秩稀疏分解重构的比较。从图2(i)SpaRcs 的低秩背景重构结果可以看出,该方法将移动前景的大部分误归为低秩背景,所以图2(j)中稀疏前景的分解结果只有部分轮廓,PCS 与CSP 方法的分解结果都优于SpaRcs 方法,从图2(d)和图2(g)可以看出,对各帧图像,本文提出的CSP 与PCS 方法结果比较,前者的稀疏前景重构结果的错误噪声点更少,前景图像更清晰。将稀疏前景与低秩背景的重构结果求和得到各帧图像的压缩感知重构结果,比较其峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)值可以看出,CSP 方法是3 种方法中最高的。 图2 Curtain 低秩稀疏分解重构结果Fig.2 The low rank and sparse decomposition refactoring results of Curtain 图3 是CSP 方法与SpaRcs 方法对Hall 视频的低秩稀疏分解重构结果的比较,实验中所有图像的压缩观测采样率都等于0.2。从图中可以看出,SpaRcs方法将人这一稀疏前景的很大一部分划分到了低秩背景中,造成稀疏前景的识别正确率很低,而CSP 方法的低秩与稀疏部分的重构结果更准确。 图3 Hall 的压缩感知低秩稀疏分解比较(m/n=0.2)Fig.3 Comparison of low rank and sparse decomposition of compressed video of Hall(m/n=0.2) 图4 所示为在压缩感知采样率为0.2~0.4 时,3 种方法对Curtain 视频所有帧重构结果的PSNR 平均值的比较。每帧的重构结果都是用重构的低秩背景与稀疏前景的和求得的。从图4 可以看出,CSP、PCS 与SpaRcs 方法比较,重构图像的PSNR 值能提高2 dB 左右,CSP 方法的PSNR 平均值高于PCS 方法。 图4 Curtain 重构图像的PSNR 平均值Fig.4 Average PSNR of Curtain reconstruction images 图5 是压缩观测采样率为0.1 时,对Hall 视频各帧图像重构结果的PSNR 值比较。从图5 结果可以看出,在相同采样率下,SpaRcs 方法重构图像的质量远低于CSP 和PCS 方法,而CSP 方法的绝大多数重构帧的PSNR 值都是3 种方法中最高的。 图5 Hall 图像压缩感知重构的峰值信噪比比较Fig.5 Comparison of PSNR of Hall image compression sensing reconstruction 图6 与图3 的各帧原图像是相同的,但压缩观测采样率变为0.3。与图3 相比,SpaRcs 方法的稀疏前景更加清晰准确,但是该方还是将视频的部分稀疏前景划分成低秩背景,与之比较,CSP 方法的低秩背景与稀疏前景的重构分解结果都更加准确。 图6 Hall 的压缩感知低秩稀疏分解比较(m/n=0.3)Fig.6 Comparison of low rank and sparse decomposition of compressed video of Hall(m/n=0.3) 本文通过将时变稀疏信号的压缩观测值投影到其低秩值的正交空间,运用重构稀疏信号值与低秩信号值的方法,实现时变稀疏信号压缩观测的低秩稀疏分解。提出压缩观测与低秩空间正交投影按不同顺序进行的两种方法,每种方法的压缩观测与投影两个过程都可分别使用各自的算子一步实现。使用相邻重构帧低秩值的结构相似度判断低秩背景是否发生变化,若发生变化,则采用最新重构低秩值更新低秩背景与其正交空间。实验结果表明,与SpaRcs 方法相比,本文方法重构图像的PSNR 平均值最多能提高2 dB 左右。后续将研究基于三维压缩感知与正交投影的压缩感知低秩稀疏分解方法,使用较少的测量数获得更高信号重构质量的三维压缩感知,对时变稀疏信号进行压缩观测,低秩正交投影在三维空间完成,在投影完成后实现稀疏与低秩信号的重构。

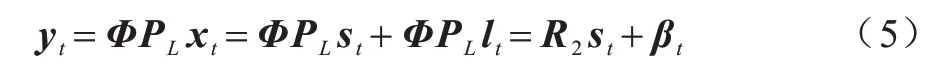
2 低秩稀疏分解的实现

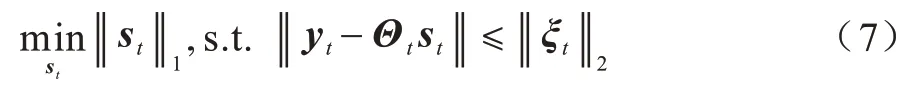

3 实验结果与分析




4 结束语

