渗流作用下富水砂层椭圆形冻结管冻结发展规律研究

白天麒，叶 超，李忠超，梁荣柱*，肖铭钊，蔡兵华

(1.中国地质大学(武汉) 工程学院，湖北 武汉 430074;2.武汉市市政建设集团有限公司，湖北 武汉 430023)

人工冻结法是通过冻结管内循环的制冷介质与土体进行换热，将地层中的水冻结，使之形成具有一定强度的冻结壁，以抵御地层水土压力的临时加固方法[1]。人工冻结施工形成稳定的冻结壁能有效地阻隔地下水和维持地层平衡，因此在城市地下空间建设中得到了广泛的应用[2-4]。

目前在人工冻结法实际施工过程中，因为圆形冻结管具有制造工艺简单、换热效果良好等优点而得到大量的应用[5-8]。但传统的圆形冻结管，单管冻结能力较弱，极大地增加了循环制冷介质用量和施工机械能耗。现有的研究主要通过调整圆形冻结管的数量、管间距、排布方式、管径等来提高地层冻结效果[6,9-10]。但这些方式都是从“量”上来提高地层冻结效果，往往伴随着较高的成本，没有从“质”上提高冻结管与土体的换热效率。

与圆形冻结管相比，椭圆形冻结管在横截面积相等的情况下周长增加，增大了冻结管与土体的接触面积，可以使制冷介质携带的冷量与周围水土充分进行冷量交换，提高了地层冻结效果。Rocha等[11]率先对椭圆形冻结管的换热问题进行了研究，结果发现椭圆形冻结管交叉排列对流换热时流动阻力降低，换热效果更为显著。我国诸多学者也对椭圆形冻结管的换热问题进行了初步有益的探索。如杨立军等[12]和王英杰等[13]研究发现，椭圆形冻结管可以减小阻力损失，增强换热系数；齐春华等[14-15]通过数值模拟和试验研究发现，椭圆形冻结管的传热效果要优于圆形冻结管。

但上述这些研究主要应用在工业领域的空调、散热器等设备当中，进行换热的介质主要为气体和液体，而在岩土工程领域中关于椭圆形人工冻结管在土体中换热效果的研究十分缺乏。

为了探究椭圆形冻结管在地层中的土体冻结规律及其影响机制，基于温度场和渗流场耦合基本理论，建立了不同截面形状椭圆形冻结管单管和双管土体冻结发展的多场耦合数值模型，模拟研究了不同冻结条件下土体冻结温度场、冻结壁厚度和冻结壁交圈时间的分布规律，相关研究结果可为提高冻结管冻结效率和人工冻结法施工效果提供新的思路。

1 椭圆形冻结管设计

图1为人工冻结法施工中常用的圆形冻结管截面示意图。在人工冻结法施工过程中通常采用直径Φ为146 mm的无缝钢管作为圆形冻结管，其截面面积S为0.016 7 m2。为了保证设计完成的椭圆形冻结管在单位时间内提供的制冷介质质量与圆形冻结管相同，要求椭圆形冻结管横截面积与圆形冻结管横截面积相等。

图1 圆形冻结管横截面示意图Fig.1 Cross-section of circular freezing pipes

图2为椭圆形冻结管的截面形状，其椭圆的形状大小主要由长轴长度a和短轴长度b控制。为了便于确定椭圆的尺寸，定义冻结管长、短轴长度的比值n为a/b。考虑钢管加工工艺和加工成本，选取n值最大为2.5，在满足椭圆形冻结管的过水面积与圆形冻结管过水面积相等的前提下，通过计算可以得到冻结管长、短轴长度的比值n分别为1、1.5、2和2.5的尺寸。表1为椭圆形冻结管的相关形状参数。

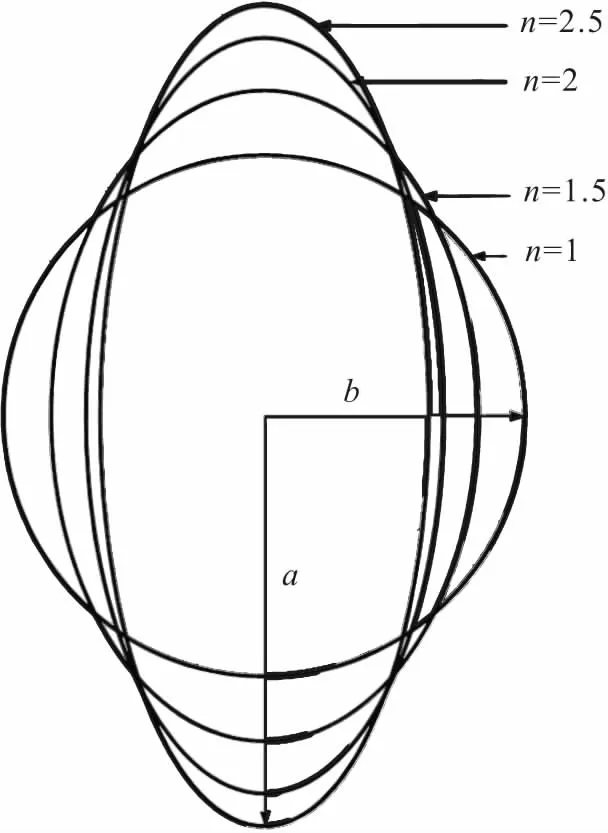
图2 不同截面形状的椭圆形冻结管Fig.2 Different section shape of elliptical freezing pipes

表1 椭圆形冻结管的相关形状参数

结合表1和图2分析发现：当冻结管长、短轴长度的比值n为1时，冻结管为圆形；冻结管长、短轴长度的比值n越大，冻结管椭圆度越大，形状越扁平。本文主要研究椭圆形冻结管长、短轴长度的比值n分别为1、1.5、2和2.5时地层的冻结效果。

2 人工冻结数值模型建立

2. 1 温度场-渗流场耦合基本理论

在人工冻结过程中，温度场-渗流场耦合是地层冻结实施的关键。为了简化计算，本文做出如下假设：①假定含水层完全饱和，总孔隙率保持不变；②假定溶质浓度引起的凝固点降低可以忽略不计；③假定土体的性质不随温度的改变而发生变化。

基于以上假设分别建立了地下水渗流场和含水层冻结温度场的控制方程。在地下水渗流场分析中，流体视为均匀稳定的达西流体，其控制方程如下：

(1)

其中：

S=Swβεp

(2)

(3)

Sw=Swres+(1-Swres)θ2

(4)

式中：S为储水模型计算中定义(1/Pa);p为压力(Pa);t为时间(s)；为向量微分算子；Sw为含水层饱和度;εp为含水层孔隙度；β含水层有效压缩系数；κ为含水层有效渗透系数(m/s);μ为含水层水力梯度;D为含水层重力势梯度(在这里忽略不考虑)；Qm为质量源[kg/(m3·s)];ρw和ρi分别为水和冰的密度(kg/m3);Swres为含水层残余水饱和度；θ2为定义在相变材料节点的平滑阶跃函数。

在冻结温度场分析中，采用多孔介质传热，其控制方程如下：

(5)

式中：(ρC)eq为流体等效体积比热[J/(kg·K)]；keq为流体有效导热系数[W/(m·K)]；T为温度(K)；T为温度梯度(K);Q为热源(W/m2)；Cw为有效流体在恒压下的热容[J/(kg·K)];u为流体的渗流速度(m/d);L为相变过程中释放的潜热(J/kg)。

上述公式(1)、(5)将渗流场与温度场进行了耦合，可为人工冻结的数值模拟提供支持，同时还考虑到实际冻结过程中的相变问题，使计算更贴合实际。

2. 2 数值计算模型建立

基于以上控制方程，利用COMSOL多场耦合软件建立了不同截面形状椭圆形冻结单管和双管冻结发展的多场耦合数值模型，模拟研究了不同冻结条件下椭圆形冻结管对地层冻结效果的影响。图3为建立的数值计算模型示意图。土层区域的几何尺寸为20 m×20 m，椭圆形冻结管的尺寸由冻结管长、短轴长度的比值n决定，主要考虑椭圆形冻结管长、短轴长度的比值n分别为1、1.5、2和2.5时地层的冻结效果。假定地层初始温度为5℃，地下水渗流从一侧流入、另一侧流出，地下水的渗流速度为5 m/d，地层为砂土层，其相关参数取值见表2。

图3 数值计算模型示意图Fig.3 Diagram of numerical calculation model

表2 砂土层主要的计算参数

3 模拟计算结果与分析

3. 1 数值计算模型验证

Wang等[16]开展了渗流条件下富水砂层圆形冻结管单管土体冻结温度场分布室内模型试验，得到不同渗流速度下土体冻结温度场的分布特征。为了验证本文建立的数值计算模型的正确性，将计算模型与模型试验[16]取相同尺寸，试验冻结管采用直径为22 mm的圆形冻结管，并将本文数值模拟的计算结果与Wang等[16]的模型试验结果进行了对比，得到不同渗流条件下圆形冻结管单管沿渗流方向土体冻结温度场分布的数值模拟计算结果与模型试验结果的对比曲线,见图4。

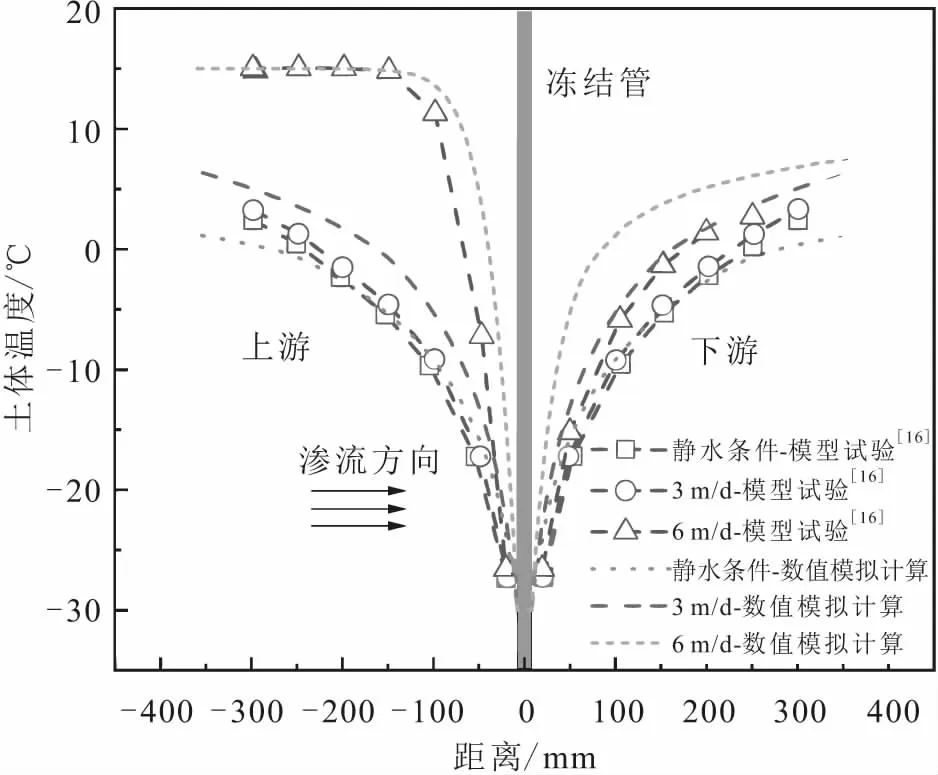
图4 不同渗流条件下圆形冻结管单管沿渗流方向 土体的冻结温度场分布图Fig.4 Soil freezing temperature field distribution along the seepage direction in single circle freezing pipes under different seepage conditons

由图4可见，本文数值模拟计算结果与模型试验结果的吻合度较高，两者土体冻结温度场的分布规律基本一致。试验和数值模拟结果反映：当处于静水条件时，冻结管两侧土体冻结温度曲线对称分布；而随着地下水渗流速度的增加，冻结管两侧上游和下游土体冻结温度曲线逐渐向不对称分布发展，且上游土体冻结温度总体上高于下游土体冻结温度，这是由于渗流作用下，地下水渗流携带冷量向下游扩散所致。总体上，采用温度场与渗流场相互耦合的数值计算方法可以反映渗流作用下土体冻结温度场的发展规律，其计算结果是准确、可靠的，故可以基于该数值计算模型进行椭圆形冻结管的土体冻结研究。

3. 2 单管冻结的对比分析

图5为不同长、短轴长度比值n的冻结管单管土体冻结250 h时的冻结温度场分布图。

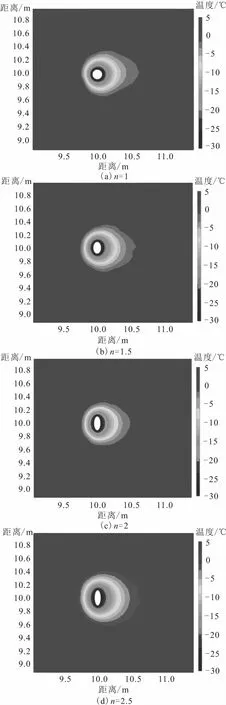
图5 不同截面形状的冻结管单管土体冻结温度场分布图Fig.5 Soil freezing temperature field distribution of single freezing pipes with different cross-section shapes

由图5可见：不同长、短轴长度比值n的冻结管单管冻结所形成的冻结壁均呈非对称的形态分布，冷锋面向冻结管下游延伸，形状类似于“滴水状”；冻结管上游土体的冻结范围较小，而冻结管下游土体的冻结范围相对较大，这与前人的研究结果较为一致[17]，这主要是由于地下水渗流带走了一定的冷量，影响冻结管上游冷量与周围水土的冷量交换；此外，随着冻结管长、短轴长度比值n的增大，土体的冻结范围增大，尤其是冻结管下游土体的冻结范围增大。

为了进一步分析冻结的影响范围，给出了不同长、短轴长度比值n的冻结管单管土体冻结区域面积，见图6。

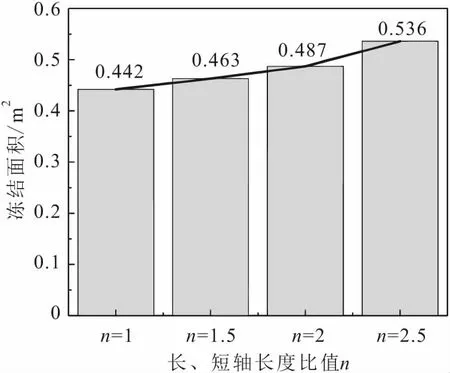
图6 不同截面形状的冻结管单管土体冻结区域面积Fig.6 Soil frozen area of single freezing pipes with different cross-section shapes

由图6可见，随着冻结管长、短轴长度比值n的增大，也就是冻结管椭圆度越大时，土体冻结区域面积相应增加。这是因为椭圆形冻结管的扁平结构使得其周长增加，有效增加了管内与邻近冻结水的冷量交换，充分发挥了冷量的热力扩散效应。

在人工冻结法施工中，冻结壁的形成是关注的重点。图7为不同长、短轴长度比值n的冻结管单管在垂直渗流方向上土体冻结壁厚度随冻结时间的发展曲线。

图7 不同截面形状的冻结管单管在垂直渗流方向土体冻 结壁厚度随冻结时间的发展曲线Fig.7 Development of the soil frozen wall thickness of single freezing pipes vertical to seepage direction of different cross-section shapes with freezing time

由图7可以发现：在地下水渗流条件下，不同截面形状冻结管单管在垂直渗流方向上土体的冻结壁发展规律基本一致，可以划分为3个阶段：冻结壁快速形成阶段(Ⅰ)、冻结壁稳定阶段(Ⅱ)和冻结壁二次增加阶段(Ⅲ)。以圆形冻结管为例，冻结开始至25 h时为冻结壁快速形成(阶段Ⅰ)，冻结壁厚度为0.28 m，此时冻结管冷量与周围水土温差较大，冷量交换程度高，使得冻结壁持续冻结发展；而后冻结壁厚度不再增加，并稳定在此数值，持续时间为100 h(阶段Ⅱ)，这是由于地下水渗流带走的冷量与土体冻结壁持续扩展所需的冷量达到了动态平衡，因而土体冻结壁厚度不再增加；当冻结管冷量持续输出，周围水土温度被进一步降低，土体冻结壁厚度再次增加，而后土体冻结壁厚度稳定在0.31 m(阶段Ⅲ)，此时冻结管冷量输出与地下水渗流携带走的冷量再次达到平衡，土体冻结壁厚度不再发展。

由图7还可以发现：在冻结阶段Ⅰ，不同截面形状的冻结管单管的冻结壁发展规律基本一致；在冻结阶段Ⅱ时，除了冻结管长、短轴长度比值n为1.5以外，其余椭圆形冻结管单管冻结引起的土体冻结壁厚度均大于圆形冻结管，而且在阶段Ⅱ时，椭圆形冻结管土体的冻结壁稳定时间均小于圆形冻结管，这是由于椭圆形冻结管周长大于圆形冻结管，其与周围水土的冷量交换效率更高、地层冻结效果更好有关；在达到阶段Ⅲ时，除了冻结管长、短轴比值n为2.5以外，其余椭圆形冻结管单管土体所需要的冻结稳定时间相比于圆形冻结管土体要大大缩小，但其土体冻结壁厚度获得了大幅增加，且冻结管越扁平其最终土体冻结壁的厚度越大。

由上述分析可知，椭圆形冻结管土体在冻结形成稳定冻结壁方面具有冻结效率高、冻结壁厚度大等明显的优势。因此，在施工中对土体形成冻结壁时间要求较短的条件下，椭圆形冻结管具有明显的优势。

3. 3 双管冻结的对比分析

将通过冻结管中心的面称作轴面，将垂直于轴面且通过冻结管中心连线中点的面称作界面，得到双管冻结计算示意图，见图8。

图8 冻结管双管布置及监测点Fig.8 Double freezing pipe layout and monitoring points

图9为不同长、短轴长度比值n的冻结管双管土体冻结250 h时的冻结温度场分布图。

心理学家曾经提出，良好的师生关系是学习环境建设的基本，只有搭建和谐平等的师生关系，强化教师和学生的互动，才可以确保学生在优良的学习环境当中学习，落实教学方式的创新运用。小学生正处在成长的青春阶段，他们更乐于根据自己对老师的喜好来开展学习，融洽良好的师生关系是提升课堂质量，加强教学质量，落实教学方法创新应用的基础条件。

由图9可见：随着n值的增大，土体冻结区域面积呈现先减小后增大的趋势，尤其是冻结管下游土体的冻结范围增大明显，土体冻结区域面积分别为1.945 m2、1.755 m2、1.912 m2、1.971 m2。

图9 不同截面形状的冻结管双管土体冻结温度场分布图Fig.9 Soil frozen temperature field distribution of double freezing pipes of different cross-section shapes

图10为不同长、短轴长度比值n的冻结管双管沿轴面方向土体冻结温度分布曲线。

由图10可以发现：在沿轴面方向上，不同截面形状的冻结管双管的土体冻结温度分布曲线以冻结管中心连线中点位置处高度对称；在冻结管中心连线中点位置处，冻结管长、短轴长度比值n越大，其土体冻结温度越低，而圆形冻结管土体的冻结温度最高。由此可见，椭圆形冻结管对双管中间土体的冻结效果优于圆形冻结管。

图11为不同长、短轴长度比值n的冻结管双管沿界面方向土体冻结温度分布曲线。

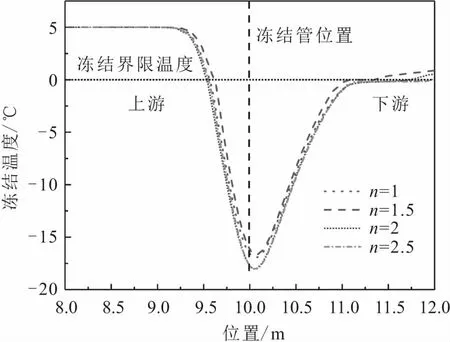
图11 不同截面形状的冻结管双管沿界面方向土体 冻结温度分布曲线Fig.11 Soil frozen temperature distribution curves along the interface direction of double freezing pipes of different cross-section shapes

由图11可以发现：不同截面形状的冻结双管土体的冻结温度曲线分布并不沿界面对称分布，土体冻结温度最低的位置并非是在冻结管中心连线中点处，而是在冻结管中心连线中点偏下游位置处。这与Wang等[18]在圆形冻结管单管中进行的渗流冻结试验的结果基本一致。其原因可能是在地下水渗流的影响下，冷量被带到冻结管下游，使冻结区域朝着下游方向移动。此外，由图11还可以发现，冻结管长、短轴长度比值n越大，土体冻结温度最低点的冻结温度越低。由此可见，冻结管越扁平，冻结冷量交换得越充分。

图12为不同长、短轴长度比值n的冻结管双管沿界面方向土体冻结壁厚度分布图。

图12 不同截面形状的冻结管双管沿界面方向土体冻 结壁厚度分布图Fig.12 Soil frozen wall thickness along the interface direction of double freeing pipes of different cross-section shapes

由图12可以发现：不同截面形状的冻结管双管，冻结管下游土体冻结壁厚度约为上游土体冻结壁厚度的2倍，其原因是冻结壁的交圈减小了地下水渗流作用对冻结管下游土体冻结区域的影响，增大了冻结管下游土体冻结区域范围；当冻结管n值为2时，冻结管上、下游土体冻结壁厚度和总冻结管厚度均为最大，其总冻结壁厚度比圆形冻结管要厚0.04 m。但值得注意的是，当冻结管n值为1.5时，土体冻结壁厚度最小。总体而言，不同截面形状的冻结管在双管冻结下土体的冻结壁厚度差异不大。

图13为不同长、短轴长度比值n的冻结管双管在测温点处土体冻结温度发展曲线。

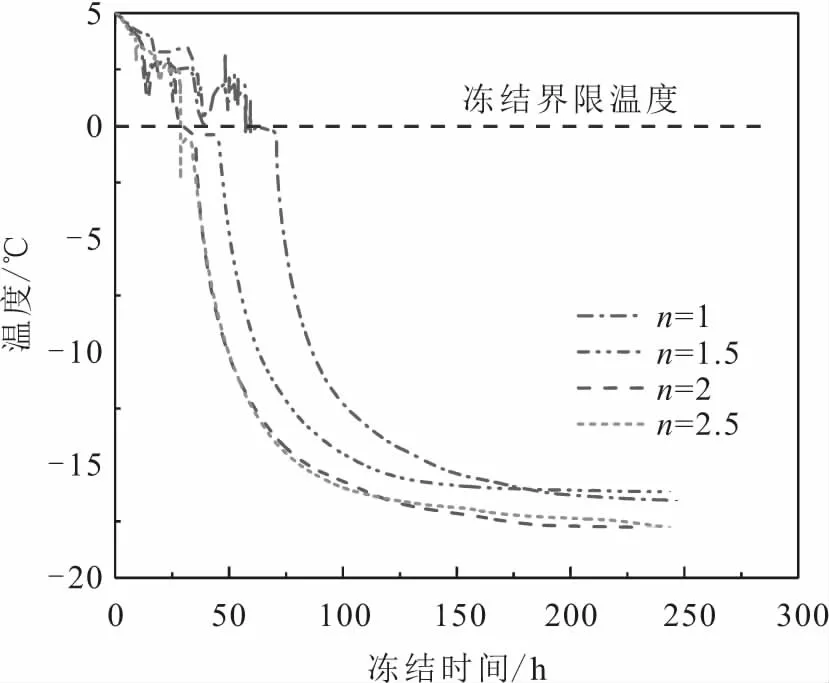
图13 不同截面形状的冻结管双管测温点处土体冻 结温度发展曲线Fig.13 Development curves of soil frozen temperature of double freeing pipes of different cross-section shapes at monitoring point

由图13可见，整个冻结过程主要分3个阶段：第一阶段为从土体开始冻结至土体达到冻结温度即冻结交圈开始阶段；第二阶段为土体温度到达冰点后温度持续下降阶段即冻结完成阶段；第三阶段为土体冻结温度逐渐稳定阶段。总体而言，冻结管越扁平，土体从初始时间冻结到冻结界限温度0℃所需的时间越短，并且土体最终冻结温度越低。此外，由图13可见，当测温点从5℃下降到冻结界限温度0℃时，长、短轴长度比值n为2和2.5的椭圆形冻结管土体需要的冻结时间约为30 h，土体最终冻结温度稳定在-17.6℃;而冻结管为圆形冻结管(n=1)则土体需要的冻结时间为70 h，所需冻结时间为前者的2.3 倍，土体最终冻结温度稳定在-16.5℃。由此可见，采用椭圆形冻结管有利于加速土体冻结过程，减少冻结时间。

图14为不同长、短轴长度比值n的冻结管双管土体冻结壁交圈和最终冻结完成形成稳定冻结壁的时间。

图14 不同截面形状的冻结管双管土体冻结壁交圈和 冻结完成的时间Fig.14 Time of frozen wall intersection start and freezing finish of double freeing pipes of different cross- section shapes

由图14可见：随着n值的增大，土体冻结壁交圈的时间提前，冻结完成的时间也缩短；尤其当n值由1提高到1.5时，土体冻结壁交圈和冻结完成的时间有明显的缩短，分别减小35%和28%；当n值继续增加到2时，土体冻结壁交圈和冻结完成的时间继续缩短，减幅达到50%；当冻结管由圆形变为椭圆形后，土体冻结完成时间有很明显的缩短，这在工程实际当中极具意义，可以在更短的时间内得到更好的地层冻结效果，极大地节约工程成本。

4 结 论

基于温度场-渗流场耦合数值计算方法，探究了在富水砂层渗流条件下椭圆形冻结管土体的人工冻结规律及其影响机制，得到以下主要结论：

(1) 在地下水渗流的影响下，椭圆形冻结管单管土体冻结区域趋向于水滴状，冻结冷锋面向冻结管下游延伸，土体冻结区域呈现“滴水状”。

(2) 椭圆形冻结管有利于管内与周围水土进行冷量交换，有效发挥冷量的热力扩散效应，使得椭圆形冻结管土体的冻结区域面积大于圆形冻结管。随着冻结管长、短轴长度比值n的增大，土体冻结区域面积相应地增加。

(3) 不同截面形状的冻结管土体冻结壁厚度的发展可以划分为3个阶段：冻结壁快速形成阶段(Ⅰ)、冻结壁稳定阶段(Ⅱ)和冻结壁二次增加阶段(Ⅲ)。椭圆形冻结管单管土体冻结壁发展速度快于圆形冻结管，冻结完成时土体冻结壁厚于圆形冻结管。

(4) 在双管冻结过程中，椭圆形冻结管土体冻结壁交圈的时间和冻结完成的时间相比于圆形冻结管有大幅的缩短，说明椭圆形冻结管可以提高人工冻结效率，节省冻结成本。