非线性效应对前向受激布里渊散射分布式传感的影响*

杨玉莲 刘黎明 邓庆雪 贾新鸿 梁文燕 姜利 宋伟杰 牟欣扬

(四川师范大学物理与电子工程学院,成都 610101)

以光力时域分析传感器为例,实验研究了非线性效应对前向受激布里渊散射分布式传感的影响,并给出了优化过程.前向受激布里渊散射的产生由于增益系数低,需要较高的脉冲功率(W级)进行激发,由于读取脉冲光与散射光同向传输特性,高功率脉冲将诱发前向受激布里渊散射传感系统中各种非线性效应.借鉴前人激活-读取分离技术,可有效避免激活脉冲非线性效应的影响,然而读取脉冲非线性效应对传感性能仍存在直接影响.基于此,本文研究了不同读取脉冲功率条件下,非线性效应对前向受激布里渊散射传感性能的影响及其物理机理;具体展示了～4.7 km 标准单模光纤中,一、二阶散射边带随读取脉冲功率的演化过程,最终找到了优化区间,得到较为完美的本地增益谱,并且延长了传感距离.

1 引言

受激布里渊散射(stimulated Brillouin scattering,SBS)是由泵浦波、斯托克斯波和声学波之间通过电致伸缩和弹光效应引起的非线性相互作用,可分为后向受激布里渊散射(backward SBS,BSBS)[1−4]和前向受激布里渊散射散射(forward SBS,FSBS).只有泵浦光注入光纤时,由热噪声激发的R0m和TR2m声学模可产生自发前向散射,称之为声波导布里渊散射(guided acoustic wave Brillouin scattering,GAWBS)[5−8].GAWBS 分为极化和去极化型,分别对应于受激类拉曼散射(stimuated Raman-like FSBS,SRLS)与受激偏振间布里渊散射(stimulated inter-polarization FSBS,SIPS);前者与R0m模有关,后者则与–45°/45° TR2m模有关[5].FSBS 已成功应用于声速测量[9]、光纤直径估计[10,11]、温度、应变[12−15]传感以及分布式光纤传感器脉冲信噪比(signal-to-noise ratio,SNR)增强[16]等.声阻抗传感应用包括点式[17−22]和分布式测量[23−30].与点式传感器相比,FSBS 分布式光纤传感由于多点同时测量能力而备受关注.与BSBS 分布式传感使用较小泵浦功率不同,FSBS 传感中W级高功率激活脉冲的注入,使其非线性影响更为强烈.值得注意的是,对于FSBS 传感器,非线性效应不仅包括自相位调制(self-phase modulation,SPM)、SPM 与群速度色散(group velocity dispersion,GVD)联合作用导致的调制不稳定性(modulation instability,MI)、受激拉曼散射(stimulated Raman scattering,SRS)、克尔-交叉相位调制(Kerr crossphase modulation,Kerr-XPM)、克 尔-四波混频(Kerr four-wave mixing,Kerr-FWM),还包括区别于BSBS、由FSBS 多级频率成分自动相位匹配所致的高阶边带影响.

对于FSBS 分布式传感,Zadok 课题组[23]提出光力时域反射(opto-mechanical time-domain reflectometry,OMTDR)技术,基于瑞利散射测量泵浦-Stokes 功率分布提取FSBS 本地谱,其性能受制于泵浦-Stokes 激活光脉冲非线性影响;Thévenaz 课题组[25]提出的本地相位恢复(local phase recovery,LPR)技术,基于激活-读取脉冲分离,有效避免了激活脉冲对所测增益谱的直接影响,但非线性效应对读取脉冲功率有着严格限制,不可忽略.董永康课题组[10,27,29]在LPR 技术基础上,引入两个读取脉冲分量(泵浦-Stokes),构成光力时域分析(optomechanics time-domain analysis,OMTDA),该方法有效提升了SNR,且可实现纳米精度包层直径分布式测量[10],但非线性效应仍会限制读取脉冲输入功率;本课题组提出基于二阶边带解调本地谱的FSBS 分布式声阻抗传感,其脉冲能量可以更加深入至光纤内部,有效提高了传感距离和SNR[30].尽管上述实验针对FSBS 分布式传感都取得了较好性能,但都受到光纤非线性的影响.因此,系统参数优化是其中的必要环节,这对于厘清各种非线性效应对FSBS 分布式传感器的影响、机理与优化途径具有重要意义.

本文以OMTDA 传感系统[10,27]为例,研究不同读取脉冲功率条件下,非线性效应对FSBS 传感性能的影响;给出了～4.7 km 标准单模光纤(standard single-mode fiber,SMF)的FSBS 边带随读取脉冲峰值功率的演化过程,最终找到了优化区间,得到较为完美的FSBS 本地增益谱.

2 实验原理

OMTDA[10,27]原理如图1 所示.双频长激活脉冲将R07模横向声场激发至稳态,目的是为了获得声子强度充分累积,并抑制由脉冲谱与FSBS 本征谱卷积引起的增益谱展宽.双频泵浦-Stokes 短读取脉冲紧跟其后,用于探测感应横向声场通过FSBS 作用产生的XPM (FSBS-XPM).两激活脉冲频率差与相位差和读取脉冲两分量频率差与相位差分别相等,并且均位于R07模横向声共振频率附近.该方法通过相干FSBS 获得传感SNR 显著增强[10,27].利用布里渊光时域分析(Brillouin optical time-domain analysis,BOTDA)探测读取脉冲泵浦-Stokes 分量功率演化,分别由P1(z)和P2(z)表示,满足下列耦合波方程[27]:

图1 OMTDA 实验原理图[10,27]Fig.1.Schematic diagram of OMTDA[10,27].

式中α为损耗系数.由 (1) 式和 (2)式可知[27]

式中Ωm为泵浦-Stokes 角频率差.利用 (3) 式和(4)式可解调FSBS 本地增益谱.

3 实验装置

实验装置如图2 所示,连续光由波长为1549.3 nm 的分布反馈半导体激光器(DFB-LD)输出,经50∶50 耦合器分为上、下两条路径.上路用于产生连续探测光,下路用于产生激活和读取脉冲.下路分支中,电光调制器(EOM2)由任意波形发生器(AWG,Tectronix AWG7082C)驱动,处于双边带载波抑制状态,产生双频激活和双频读取脉冲;扰偏器(PS2)具有抑制BSBS 偏振噪声以及抑制TR2m模GAWBS 影响的双重作用.上路分支由微波源(MWS)驱动,经过载波抑制EOM1产生双边带连续光;偏振扰偏器(PS1)对连续光进行扰偏,以克服偏振相关增益波动;通过掺铒光纤放大器(EDFA1)对连续光进行放大;可调谐带通滤波器(TBPF1)用于滤除放大噪声以及产生单边带探测光,再经过EDFA2 二次放大注入待测光纤;TBPF2 和PD1 用于监测脉冲状态.如图1 所示,探测光与光源频差分别以vB−vFSBS/2或vB+vFSBS/2(νB与νFSBS分别为BSBS 与FSBS 布里渊频移)为中心扫频(范围60 MHz,步长3 MHz),将所得增益谱求和(抑制BSBS 布里渊频移波动影响[27])可分别得出读取脉冲泵浦与Stokes 分量功率分布;类似地,调整探测光与光源频差,使探测光与激活或读取脉冲二阶边带频差以νB为中心扫描,可得出对应分量功率分布.接收端的带通滤波器(BPF,带宽 <0.1 nm)用于滤除端面反射与瑞利散射.数据采集卡(DAQ)对探测器(PD2)收集的信号进行采集,采样率为100 MSa/s.

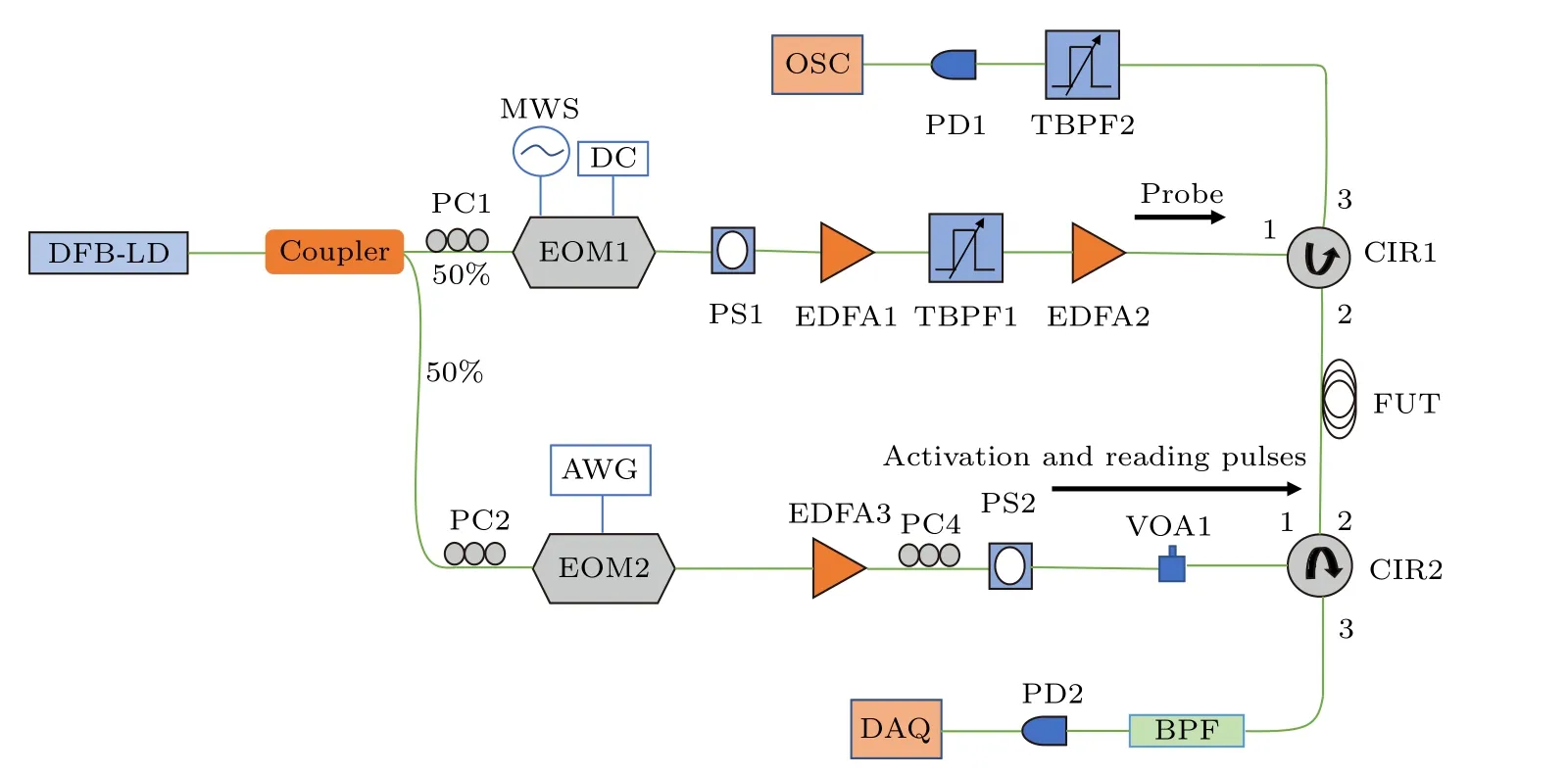
图2 OMTDA 实验装置.Coupler,耦合器;DFB-LD,分布式反馈激光器;EOM,电光调制器;MWS,微波源;DC,直流电压;PC,偏振控制器;PS,偏振扰偏器;EDFA,掺铒光纤放大器;CIR,环形器;TBPF,可调谐带通滤波器;AWG,任意波形发生器;BPF,带通滤波器;VOA,可变光衰减器;FUT,待测光纤;PD,光电探测器;OSC,示波器;DAQ,数据采集卡Fig.2.Experimental setup of OMTDA.DFB-LD,distributed feedback laser diode;EOM,electro-optic modulator;MWS,microwave source;DC,direct current;PC,polarization controller;PS,polarization scrambler;EDFA,erbium-doped fiber amplifier;CIR,circulator;TBPF,tunable bandpass filter;AWG,arbitrary waveform generator;BPF,bandpass filter;VOA,variable optical attenuator;FUT,fiber under test;PD,photodetector;OSC,oscilloscope;DAQ,data acquisition card.

4 结果与讨论

实验中使用约4.7 km 长的SMF 作为待测光纤,光纤约1.5 km 处利用丙酮溶液剥离光纤涂覆层,在一定程度上抑制涂覆层对声波的吸收,从而增强声子寿命.激活脉宽设置为400 ns,将横向声波场激发至稳态;探测脉宽为100 ns,对应10 m 空间分辨;连续光入纤功率为–5 dBm;激活脉冲峰值功率为1.58 W.FSBS 扫频范围为318 —326 MHz,单次扫描平均次数为300,扫描步长为0.2 MHz.探测光与读取脉冲作用时,激活脉冲仍与之存在BSBS 作用.调节激活、读取脉冲之间的频率间距发现:激活脉冲串扰随二者频率间距增大而减弱[29];当激活、读取脉冲频率间隔达到约2 GHz 时,串扰可忽略不计.

图3(a)和图3(b)分别为激活脉冲低频和高频分量归一化功率分布.很显然,低频脉冲在初始阶段经历了明显的放大.约超过1500 m 时,激活脉冲低频与高频分量功率几乎均降到零.考虑到所用泵浦功率均为瓦级,远超过MI 与SRS 阈值功率(分别约为100 与600 mW[31]).由于MI 使脉冲部分能量转移至两个边带,并且SRS 使部分能量转移至距激活脉冲频率约10 THz 的低频边带,导致所测激活脉冲功率急剧下降[32].但是由于同向传输导致的自动波矢匹配特性,MI 边带与SRS 边带的双频脉冲分量FSBS 作用感应声场仍具有相干作用,激活脉冲MI 和SRS 对FSBS 激发效率并无明显影响.同样条件下,可以看到读取脉冲在约1500 m 后能量依然存在,甚至可延伸至约4000 m,如图4—图7 所示.这些图形给出了使用不同功率的读取脉冲时,FSBS 增益谱响应结果,其中读取脉冲峰值功率依次为1.38,0.69,0.36 和0.16 W.图4—图7 中,(a)和(b)分别给出了FSBS 低频和高频的二维(2D)增益谱响应,图中黑色虚线表示低频最高峰与高频最低峰对应的距离-频移图;经差分处理得出的本地FSBS 增益谱如各图中的(c)所示;并给出了低频最高峰与高频最低峰对应的归一化功率分布(图(d)).下文中,为比较不同条件下的非线性传感影响,将所测读取脉冲与二阶边带功率分布相对于1.38 W 读取脉冲峰值功率分布的最大值作归一化.

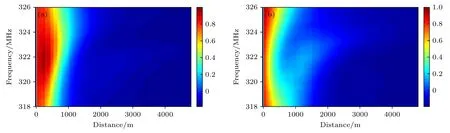
图3 激活脉冲的(a)低频和(b)高频分量归一化功率分布Fig.3.Power distribution of (a) low frequency and (b) high frequency components of activation pulses.

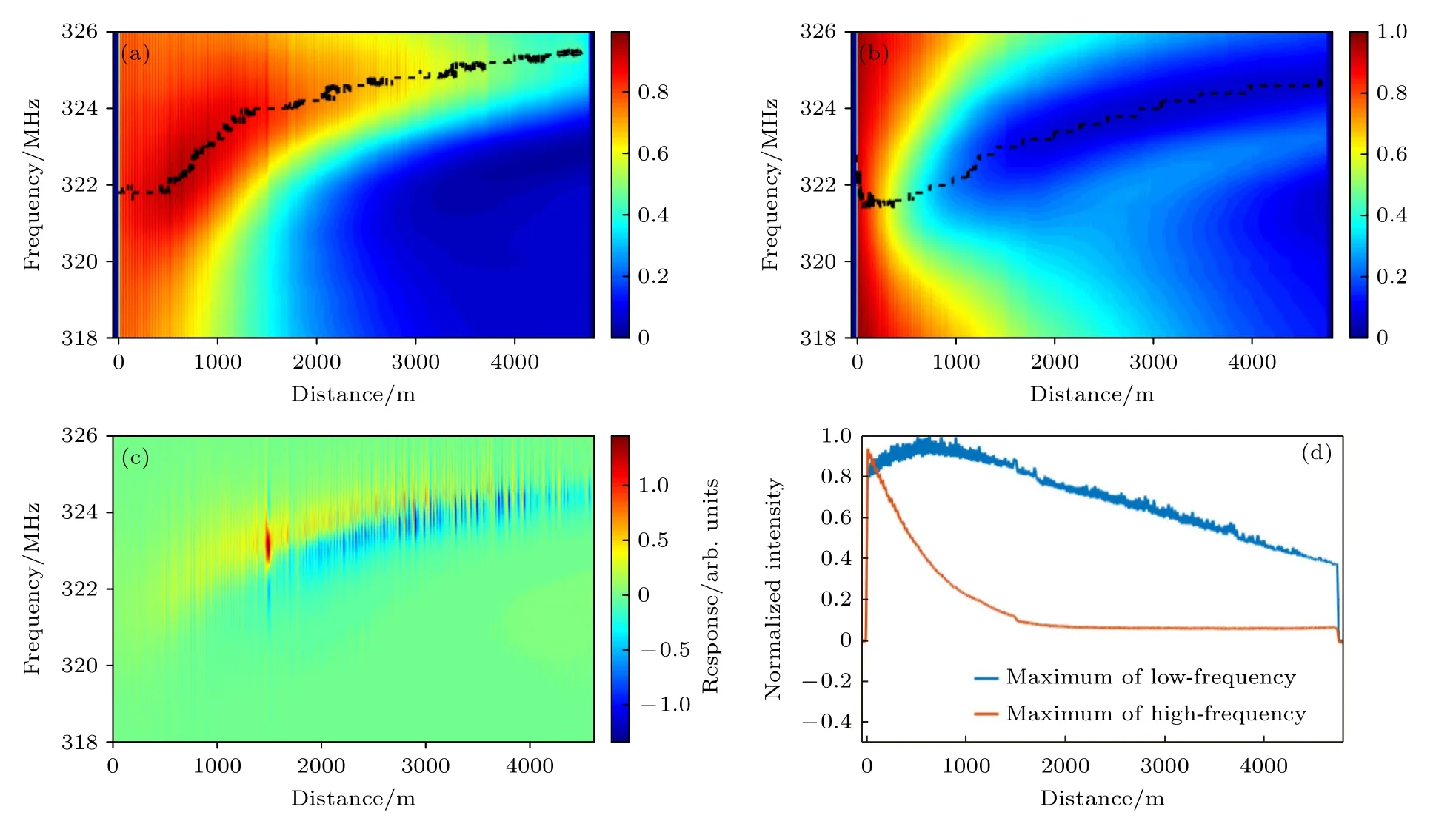
图4 读取脉冲峰值功率为1.38 W 时,FSBS 的(a)低频和(b)高频归一化功率分布,(c)差分后二维(2D)增益谱以及(d)低频最高峰与高频最低峰对应的归一化功率分布Fig.4.(a) Low-frequency,(b) high-frequency normalized power distribution,(c) post-processing 2D gain spectrum,and (d) normalized power distribution for the highest peak of low-frequency and lowest peak of high-frequency when the peak power of the reading pulse is 1.38 W.

由于读取脉冲受到激活脉冲FSBS 感应的横向动态光栅(transverse dynamic grating,TDG)作用,并且其高频与低频相位差与激活脉冲保持一致,使得低频读取脉冲功率表现为增益,而高频读取脉冲则受到消耗作用[10,27].因此理想情况下,低频分量功率分布随扫频呈对称凸起状;而高频分量功率分布则为对称凹陷状.从图4(a)和图4(b)可以看出,读取脉冲的高频与低频功率分布表现出严重的频移非对称性(高频最小峰与低频最大峰对应频移逐渐偏离R07声模共振频率(约322 MHz)).相应地,提取的FSBS 本地谱表现出严重的扭曲失真,限制了传感SNR 与距离(见图4(c)).这可能与读取脉冲Kerr-XPM 和FSBS 相干叠加形成的Fano共振[25]有关;此外,Kerr-FWM 与级联的FSBS效应使得不同边带之间产生复杂的能量转移,从而加剧了功率分布与本地增益谱的频移非对称性.

从图4(a)和图4(b)还可以看出,读取脉冲高频与低频分量功率沿传感距离整体表现出一定的下降趋势.这是因为读取脉冲峰值功率过高(1.38 W),出现了MI 和SRS 的联合效应,能量提前衰减,从而影响传感距离(读取脉冲峰值功率为0.69 W 的图5 也出现类似情况).

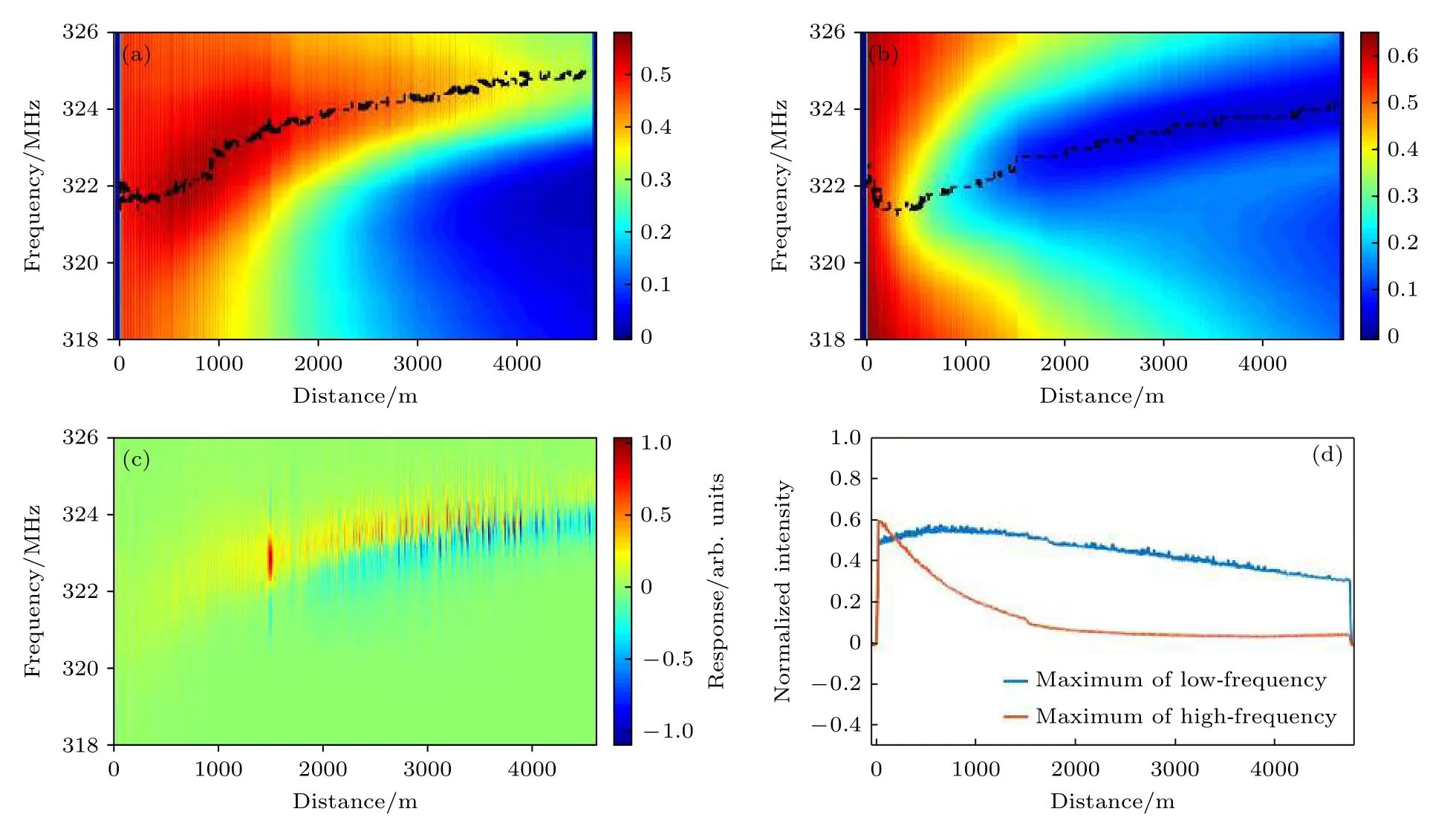
图5 读取脉冲峰值功率为0.69 W 时,FSBS 的(a)低频和(b)高频归一化功率分布,(c)差分后2D 增益谱以及(d)低频最高峰与高频最低峰对应的归一化功率分布Fig.5.(a) Low-frequency,(b) high-frequency normalized power distribution,(c) post-processing 2D gain spectrum,and (d) normalized power distribution for the highest peak of low-frequency and lowest peak of high-frequency when the peak power of the reading pulse is 0.69 W.

减小读取脉冲的峰值功率时,FSBS 传感的非线性影响逐渐减弱,表现为读取脉冲高频与低频分量功率分布、以及FSBS 本地增益谱非对称性逐渐好转(见图4—图7 所示变化过程;图4—图6 中频移非对称性起始点分别约为0.5,1,1.2 km).当读取脉冲峰值功率减小到一定程度后(0.3—0.1 W),增益谱变化不大,非对称性明显减少,非线性效应对传感的影响显著减弱,此时传感SNR 较好的区域得到扩展,MI 与SRS 引起的功率分布下降可忽略(图6 和图7).实验还观察到,当读取脉冲功率低于～0.1 W 后,SNR 将显著恶化(图中未画出).需要说明的是,图7(c)中,FSBS峰值频移沿光纤的变化是由于包层直径的改变引起的[10,11].

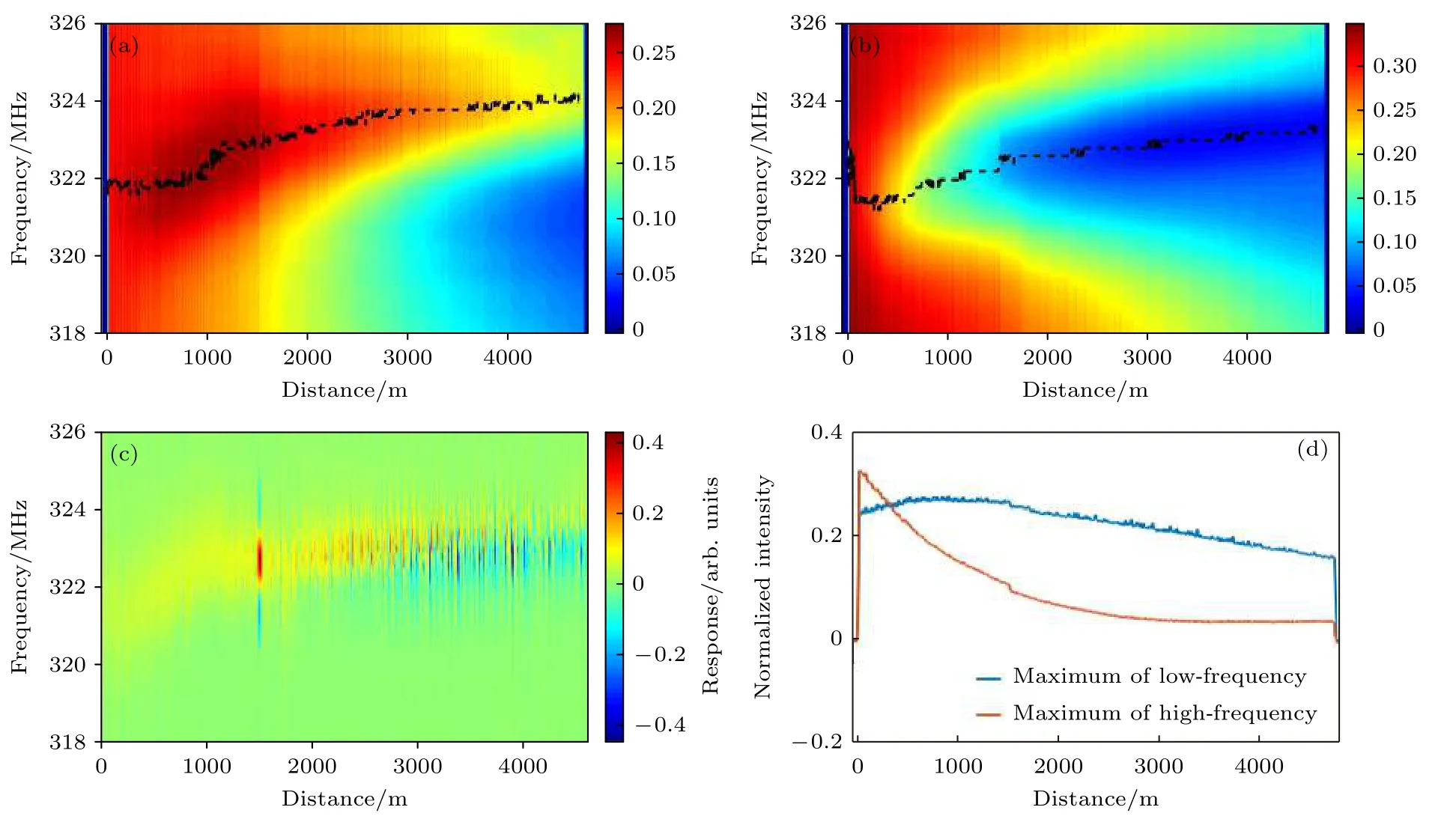
图6 读取脉冲峰值功率为0.36 W 时,FSBS 的(a)低频和(b)高频归一化功率分布,(c)差分后2D 增益谱以及(d)低频最高峰与高频最低峰对应的归一化功率分布Fig.6.(a) Low-frequency,(b) high-frequency normalized power distribution,(c) post-processing 2D gain spectrum,and (d) normalized power distribution for the highest peak of low-frequency and lowest peak of high-frequency when the peak power of the reading pulse is 0.36 W.

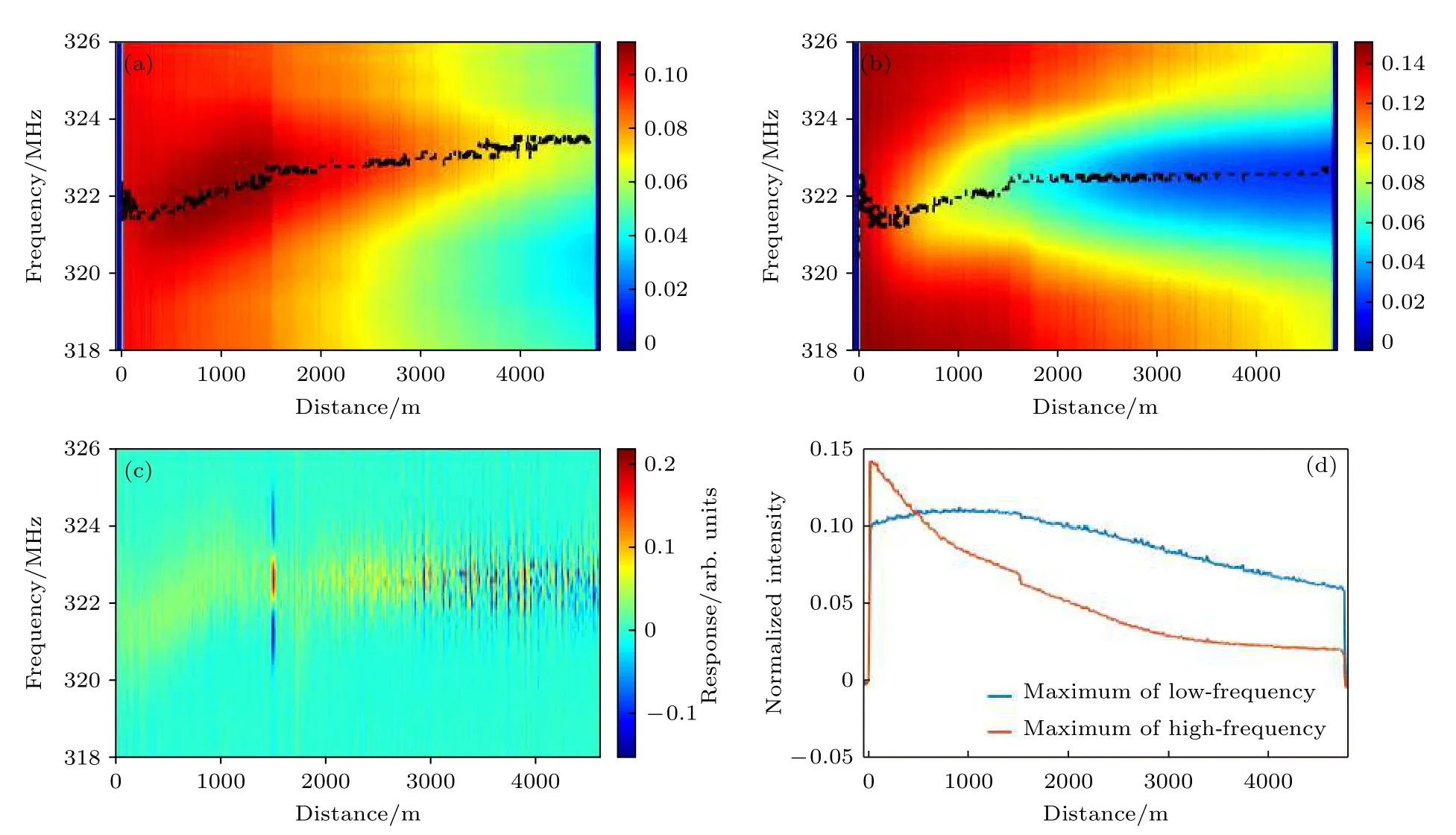
图7 读取脉冲峰值功率为0.16 W 时,FSBS 的(a)低频和(b)高频归一化功率分布,(c)差分后2D 增益谱以及(d)低频最高峰与高频最低峰对应的归一化功率分布Fig.7.(a) Low-frequency,(b) high-frequency normalized power distribution,(c) post-processing 2D gain spectrum,and (d) normalized power distribution for the highest peak of low-frequency and lowest peak of high-frequency when the peak power of the reading pulse is 0.16 W.

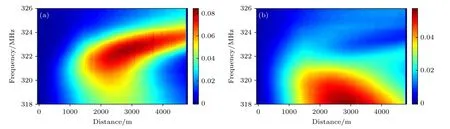
图8 读取脉冲峰值功率为1.38 W 时,二阶FSBS 边带的(a)低频与(b)高频分量归一化功率分布Fig.8.Normalized power distribution of (a) low frequency and (b) high frequency components of 2nd-order FSBS sidebands when the peak power of the reading pulse is 1.38 W.

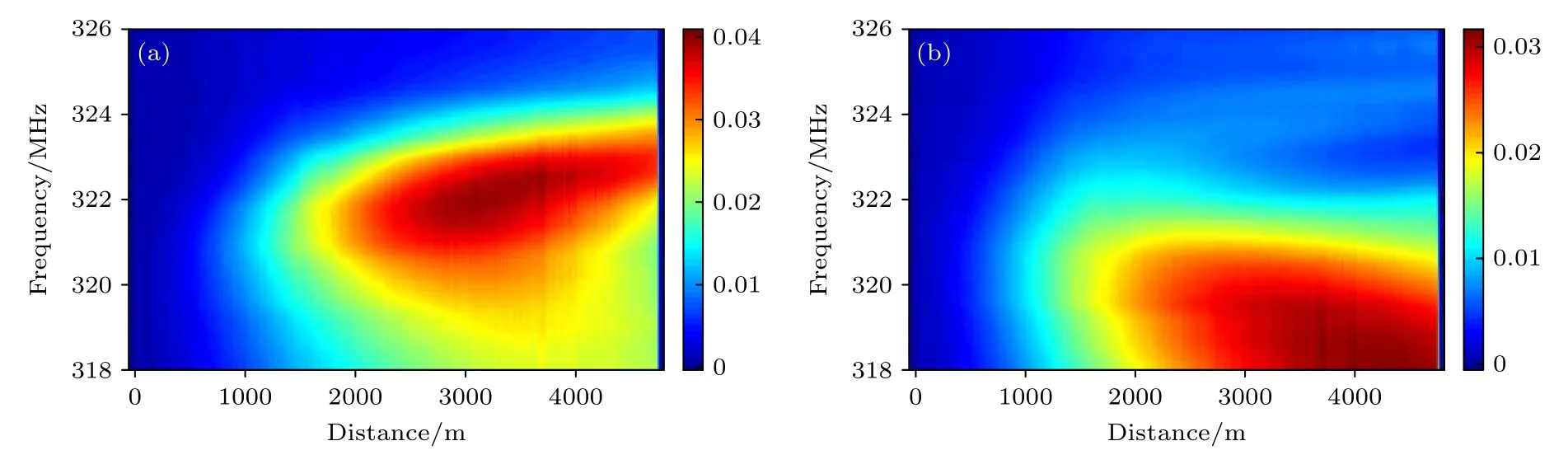
图9 读取脉冲峰值功率为0.69 W 时,二阶FSBS 边带的(a)低频与(b)高频分量归一化功率分布Fig.9.Normalized power distribution of (a) low frequency and (b) high frequency components of 2nd-order FSBS sidebands when the peak power of the reading pulse is 0.69 W.

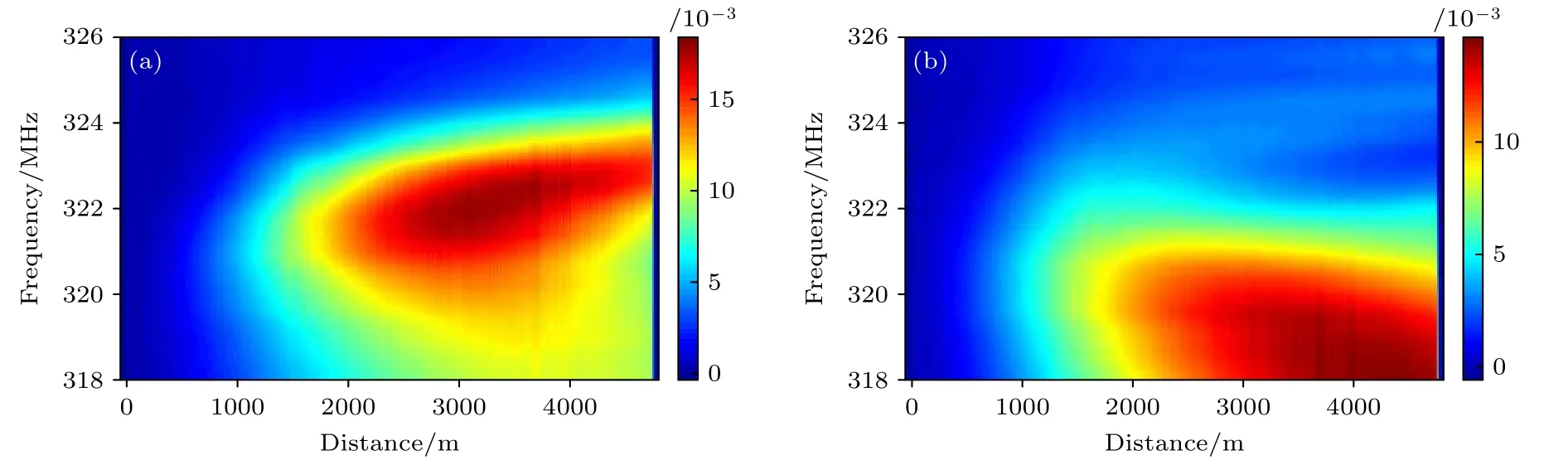
图10 读取脉冲峰值功率为0.36 W 时,二阶FSBS 边带的(a)低频与(b)高频分量归一化功率分布Fig.10.Normalized power distribution of (a) low frequency and (b) high frequency components of 2nd-order FSBS sidebands when the peak power of the reading pulse is 0.36 W.

为进一步探究级联FSBS 和Kerr-FWM 等非线性效应的传感影响机理,图8—图11 给出了不同读取脉冲峰值功率条件下,二阶边带高频(图(b))与低频(图(a))分量归一化功率分布.对比可知,读取脉冲峰值功率愈高,转移到边带的能量愈多.与前述图4—图7 对应,当功率为1.38 W 时,边带功率分布也呈现出强烈的频移非对称性,这一特性与前述一阶边带功率分布类似.这表明不同边带间存在复杂的非线性相互作用.当读取脉冲峰值功率降到0.1—0.3 W(低于SRS 阈值,接近MI 阈值)时,如图11 所示,二阶边带得到明显抑制,此时能量大部分集中在一阶边带上,可获得较好的传感效果.因此,实验证实了读取脉冲功率并不是越高越好,并体现了优化过程.

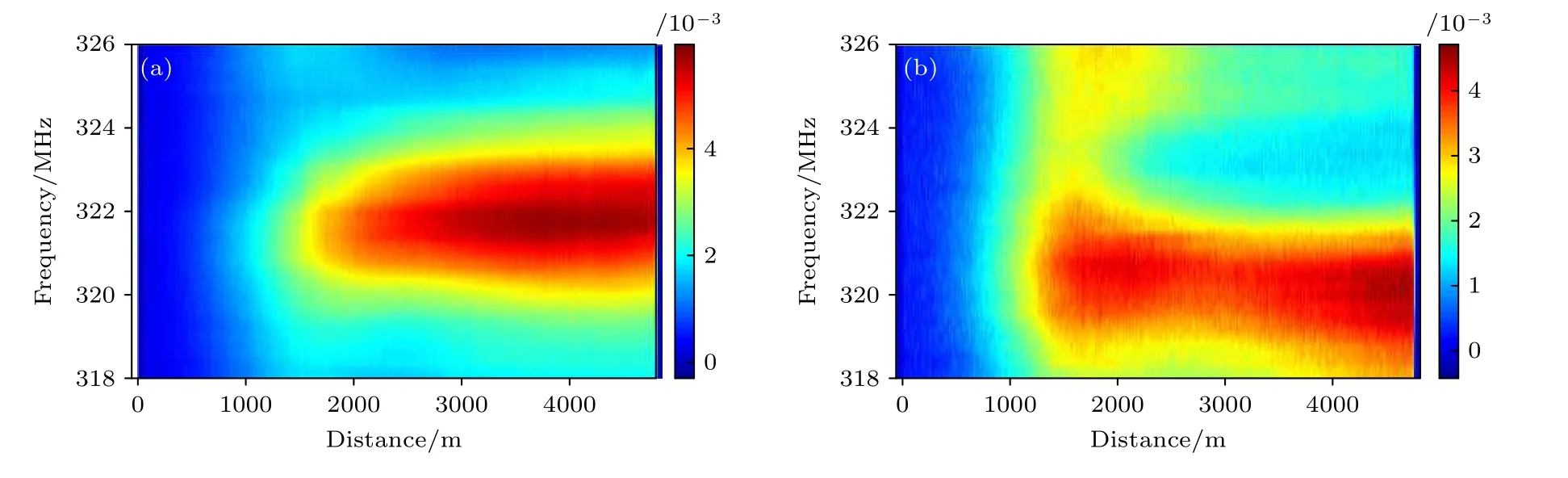
图11 读取脉冲峰值功率为0.16 W 时,二阶FSBS 边带的(a)低频与(b)高频分量归一化功率分布Fig.11.Normalized power distribution of (a) low frequency and (b) high frequency components of 2nd-order FSBS sidebands when the peak power of the reading pulse is 0.16 W.

5 结论

本文以OMTDA 传感系统为例,结合BOTDA探测技术,实验研究了不同功率读取脉冲下非线性效应对FSBS 分布式传感的影响,并进行了优化研究.研究发现,当读取脉冲峰值功率较高时(达到W级),FSBS 增益谱严重展宽且出现扭曲,这是由较高功率诱发的联合非线性效应所致.对读取脉冲功率进行了优化研究,给出了4.7 km SMF 中,不同读取脉冲峰值功率下一阶、二阶边带FSBS 增益谱强度、形状的变化过程,并找到了一个较好的功率优化区间,使得非线性效应影响与传感SNR 达到较好平衡.本研究对于厘清各种非线性效应对FSBS 分布式传感的影响、机理与优化途径具有重要意义.