基于面磁荷密度的金属磁记忆检测正演模型*

罗旭 王丽红 吕良 曹书峰 董学成 赵建国

1) (成都理工大学机电工程学院,成都 610059)

2) (河北石油职业技术大学热能工程系,承德 067000)

3) (西南石油大学机电工程学院,成都 610500)

磁偶极子理论在金属磁记忆检测正演分析中得到了广泛应用,但是现有模型中的磁荷密度多为假设值,且假设磁荷在缺陷断面或应力集中区域呈均匀分布或线性分布,无法实现磁记忆信号的准确定量分析.针对上述问题,本文在结合力磁耦合理论、磁荷理论和有限元方法基础上,将试件离散为有限多个微小单元,假设单元内部磁特征参数分布均匀,建立了单元应力、磁化强度与磁荷密度之间的关系,构建了能够考虑应力不均匀分布对磁荷密度分布影响的金属磁记忆检测正演模型.与实验结果对比发现,本文建立模型无论是定性还是定量上都能很好预测磁记忆信号变化规律;在此基础上,对比了应力集中和宏观裂纹表面磁场分布的差异,并以裂纹缺陷为例,详细讨论了裂纹缺陷尺寸参数对磁记忆信号及其特征参量的影响规律.理论分析表明,本文模型可为定量分析磁记忆检测过程中缺陷附近磁场变化规律提供新的理论模型.

1 引言

1994 年,俄罗斯学者Dubov 教授[1]最早提出一种新型无损检测方法—金属磁记忆检测法,该技术自问世以来,便受到国内外学者的广泛关注,被誉为“21 世纪崭新的无损检测技术”.与传统漏磁检测方法不同,金属磁记忆检测作为一种被动式的弱磁检测技术,不需要额外施加激励磁场,在应力-应变、材料微观变化和地磁场的联合作用下,会在应力集中、塑性变形、微观缺陷等局部损伤区域表面形成自发漏磁场,理论上通过分析自发漏磁场的分布、幅值等,就可以得到损伤的位置、大小等信息.

建立金属磁记忆正演模型,准确描述应力、缺陷和磁记忆检测信号之间的定量关系,是实现磁记忆检测技术工程应用需要解决的基础问题之一.目前,基于磁荷理论的正演模型在磁记忆检测信号分析中得到了广泛应用.Wang 等[2,3]假设磁荷在塑性变形区域和表面呈线性对称分布,建立了反映塑性变形区域磁场分布的磁偶极子正演模型;万强等[4]利用一维Z-L 模型建立了应力与磁化强度之间的关系,将缺陷应力集中区域等效为磁偶极子,建立了反映应力集中区域磁记忆信号特征的解析模型;Leng 等[5]根据断口周围硬度值分布规律,假设裂纹边缘位错分布与磁偶极子分布一致,将磁偶极子密度表示为与裂纹边缘之间距离的线性位置函数,建立了基于位错分布的磁偶极子正演模型;Leng 等[6]假设磁荷在应力集中区域和V 型缺口表面呈线性分布,建立了应力集中区域和V 型缺口的磁偶极子正演模型;徐明秀等[7]假设磁荷在塑性变形区域边界面均匀分布,在裂纹断面处呈线性分布,推导了适用于疲劳损伤分析的磁偶极子正演模型;Shi 和Zheng[8]在考虑应力集中区域宽度影响的基础上,建立了塑性变形区域的三维磁偶极子正演模型;时朋朋和郝帅[9]结合Z-L 模型,建立了力磁耦合型磁偶极子正演模型,并基于二维磁偶极子简化,实现理论模型的解析求解.

上述模型利用静磁学理论能够简单、方便地计算缺陷表面磁场分布,对分析缺陷表面磁场分布规律起到了极大促进作用,但存在的问题也十分明显.首先,磁偶极子正演模型的关键是要确定磁荷密度大小,而现有磁偶极子正演模型中磁荷密度多为假设值,分析过程多采用归一化形式分析磁信号变化趋势;其次,现有磁偶极子正演模型多假设磁荷在缺陷断面或应力集中处呈均匀分布或线性分布,这与缺陷附近磁荷密度非均匀分布情形不符;最后,现有磁荷模型只能描述规则形状缺陷,且不同形状缺陷的磁荷模型形式不同.

针对现有磁偶极子模型存在的问题,本文在结合力磁耦合模型、磁荷理论和有限元方法基础上,通过将试件离散为有限多个微小单元,假设每个单元内部磁特征参数分布均匀,建立了单元应力、磁化强度与磁荷密度之间的关系,构建了能考虑应力不均匀分布对磁荷密度分布影响的金属磁记忆检测正演模型,并通过与已有实验结果对比,验证了本文模型的正确性;在此基础上,对比了含应力集中和宏观裂纹缺陷试件表面磁场分布的差异,并以裂纹缺陷为例详细讨论了裂纹缺陷尺寸参数对磁记忆信号及其特征参量的影响规律,为定量分析缺陷表面的磁记忆信号变化规律提供新选择.

2 力磁耦合模型

在不考虑温度变化和磁滞效应影响条件下,磁致伸缩材料单位体积三维弹性Gibbs 自由能可写为[10−13]

对于各向同性材料,(6)式和(7)式中相关张量函数可以表示为[11−13]

(9)式和(10)式即非磁滞条件下铁磁材料的三维非线性力磁耦合本构模型的一般形式.

在工程应用过程中,铁磁材料构件(如硅钢片、板材)一般可视为二维薄板结构,因此在实际应用时可以将(9)式和(10)式简化为二维形式,即:

式中c表示可逆系数.

当考虑由于钉扎效应产生的磁滞损耗时,根据能量守恒原理可得

式中K为钉扎系数.

联立(13)式—(16)式可得

式中,

(17)式即为考虑磁滞效应的铁磁材料磁化强度随应力的变化关系模型.

3 基于面磁荷密度的磁记忆信号计算模型

金属磁记忆检测本质上属于磁无损检测,其正演问题可归结为求解地磁场条件下的Maxwell 方程.在磁记忆检测过程中,作为激励源的地磁场在小范围内可以认为是均匀分布的静磁场,且铁磁体内部没有传导电流,Maxwell 方程组可以简化为[18−20]

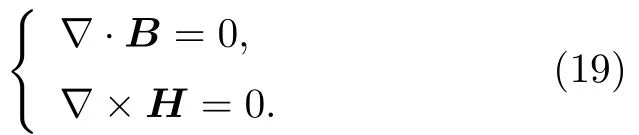
在磁记忆检测中,由于没有传导电流,因此可以引入标量磁位φm来描述磁场强度H:

标量磁位φm的积分形式可以写为[18]

由于应力的不均匀分布,导致铁磁体内部磁化强度分布不均,磁化强度M是关于源点 (ξ,η,ζ) 应力的非线性函数,很难通过直接积分求得φm解析解.因此,在实际计算过程中,可将铁磁体离散为N个微小体积单元,则每个单元的磁化强度Me可认为是常数,即∇′·Me0,ρm=0,代入(21)式中,则每个单元的标量磁位φe,m可以简化为[18]

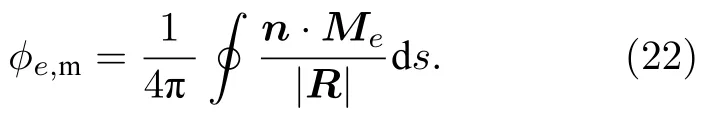
将(22)式代入(20)式,则每个单元的磁场强度分量可写为[20]

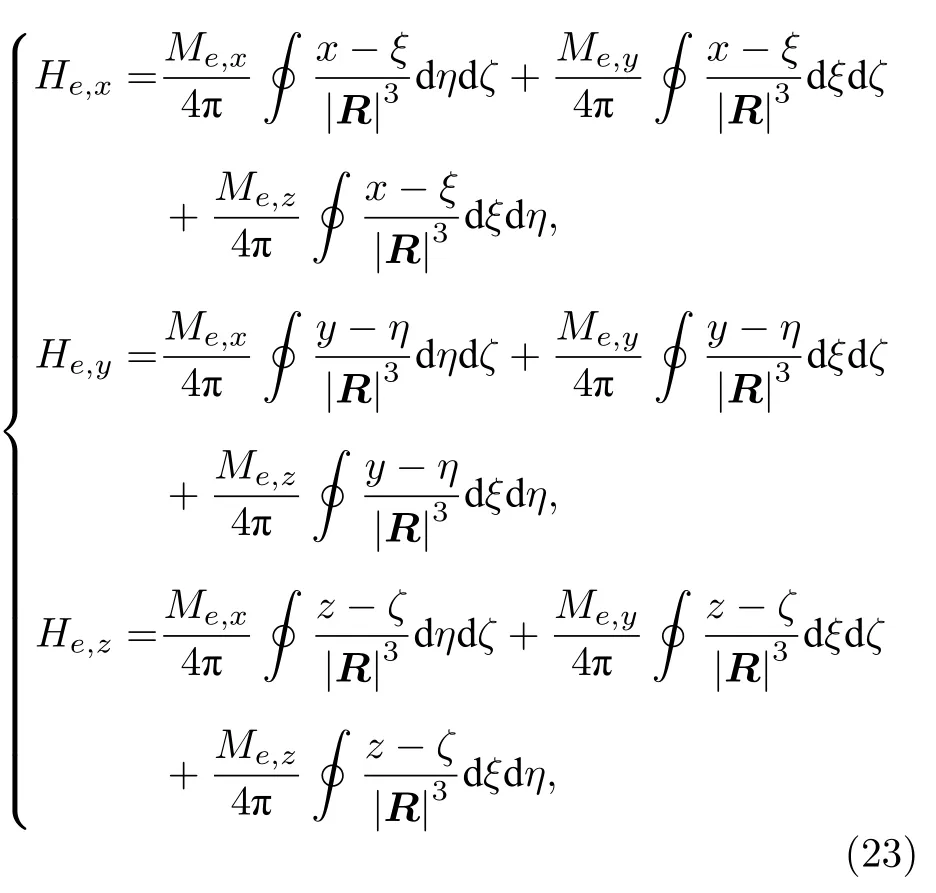
式中,Me,x,Me,y和Me,z分别表示第i号单元内的磁化强度Me在x,y,z方向上的分量.

(23)式中,被积函数只与场点和源点的位置有关.因此,第i号单元在场点处产生的磁场强度可以用一个与源点坐标和场点坐标相关的3×3 阶矩阵来表示,并将该矩阵定义为面积分耦合系数矩阵(23)式可以简写为

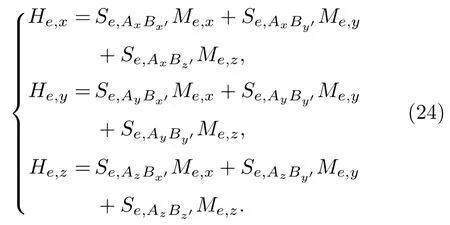
将单元铁磁体磁场强度进行求和,即得到整个铁磁体周围空间任意一点处的磁场强度:

(26)式即为基于等效面磁荷积分的金属磁记忆信号计算模型,要对其进行求解,还需建立离散单元面积分耦合系数矩阵以任意六面体单元为例,根据(25)式可知,由六面体单元顶点坐标计算面积分耦合系数矩阵的关键是求解以下三类积分式[20]:

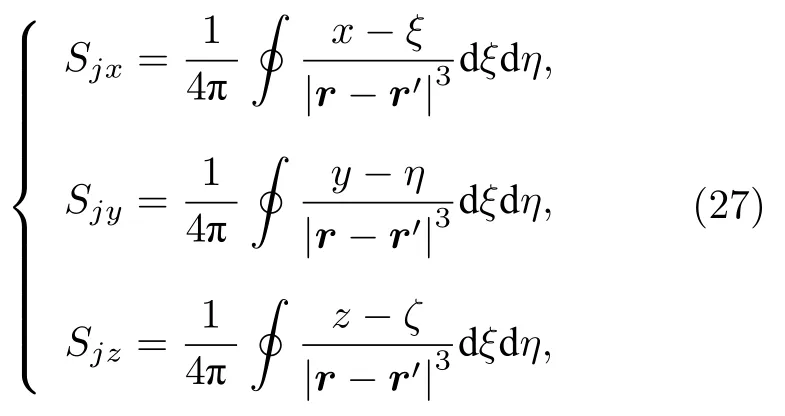
式中Sj为六面体单元的第j号空间表面,j1,2,···,6.随着六面体单元形状、空间位置离散方案不同,要得到全局坐标系下面积分耦合系数矩阵的解析式是十分困难的.因此,为获得六面体每个表面的面积分耦合系数,需要将每个外表面旋转到局部坐标下,使得该表面成为相对局部坐标系的水平面,如图1 所示[18−20].

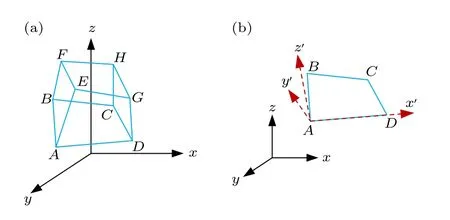
图1 任意形状六面体单元及局部坐标示意图 (a) 任意形状六面体单元示意图;(b) 六面体单元表面 Sj 局部坐标示意图Fig.1.Sketch of an irregular hexahedron element and its local coordinates:(a) Sketch of an irregular hexahedron element;(b) local coordinates of the surface Sj of irregular hexahedron element .

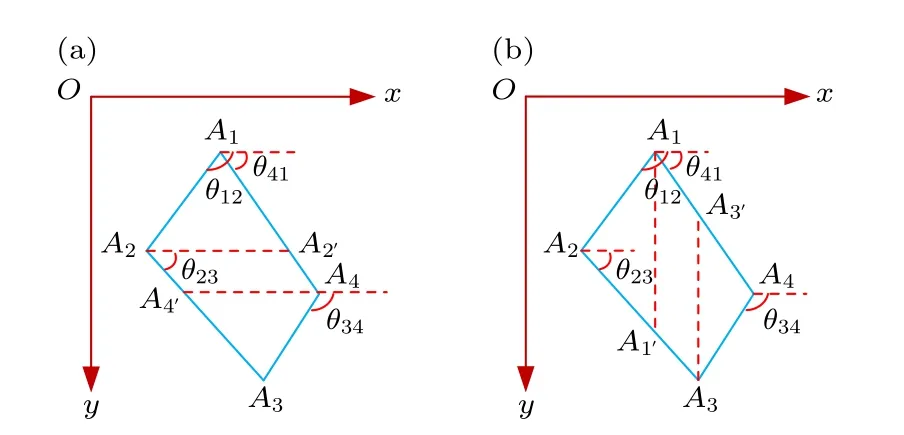
图2 任意四边形面积分示意图 (a) 平行于x 轴,任意四边形分域积分示意图;(b) 平行于y 轴,任意四边形分域积分示意图Fig.2.Sketch of surface integral of an irregular quadrangle:(a) Surface integral of an irregular quadrangle parallel to the x axis;(b) surface integral of an irregular quadrangle parallel to the y axis.

(28)式—(31)式中的下标j表示多面体第j号空间表面的相应参数值.逐一计算各个空间表面的面积分耦合系数,然后相加就可得到任意多面体的面积分耦合系数.则全局坐标系下,任意多面体单元面积分耦合系数可以写为

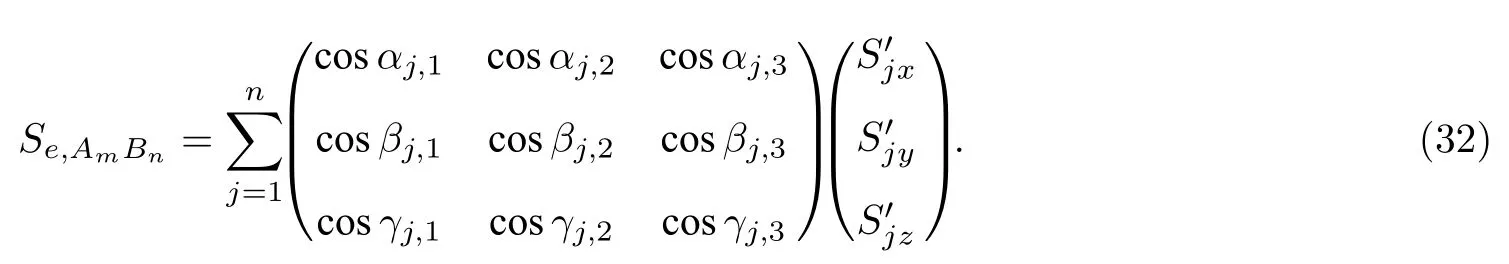
则对于每个多面体单元的磁场三个分量的等效面磁荷积分解析表达式为

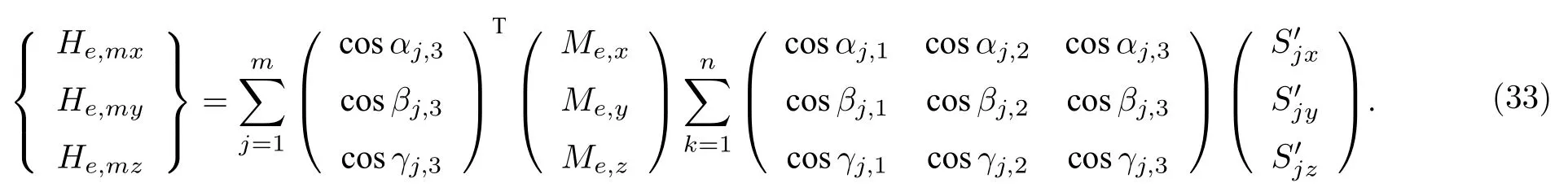
因此,对于整个铁磁体而言,磁场三个分量的等效面磁荷积分解析表达式则为

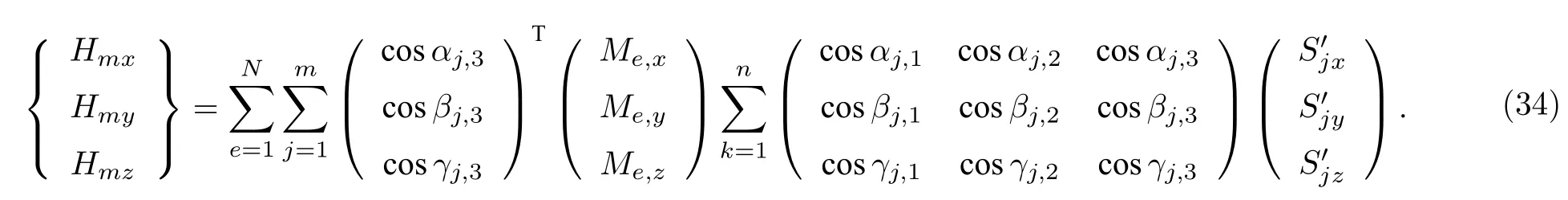
联立(17)式—(34)式可实现金属磁记忆检测信号的正演计算.

4 模型验证与讨论

在计算过程中,首先将含不同类型、尺寸缺陷试件的几何模型离散为有限多个微小单元,利用有限元方法计算试件应力分布;然后,假设每个单元磁特征参数分布均匀,利用(17)式计算每个单元的磁化强度,再利用磁化强度与磁荷密度之间的关系确定单元磁荷密度大小;在此基础上,利用(34)式计算试件表面磁场分布情况.计算流程如图3 所示.

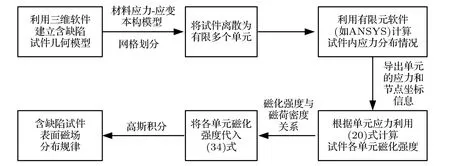
图3 基于面磁荷密度的金属磁记忆正演计算流程Fig.3.Calculation flowchart of metal magnetic memory forward analysis based on surface magnetic charge density.

4.1 模型验证

为说明本文正演模型的计算效果,采用该模型计算图4 所示含有槽形裂纹缺陷的铁磁试件的磁场水平分量Hx和法向分量Hz分布,其中缺陷长Lc=4 mm、宽Wc=2 mm、深Dc=2 mm,地磁场强度H040 A/m,方向与x平行;试件所受拉伸应力σ050 MPa,测试线位于试件中部缺陷正上方,测试线距离试件表面的高度定义为提离高度L,当提离高度L1,2,3 mm .假设材料为各向同性材料,模型中λs4.17×10−6m,Mws1.35×106A·m−1,Ms1.6×106A·m−1,β1.4,ϑ0.75,a0900,(Nd)kkNd5×10−5,k1.52×10−3A/m,α1.44×10−3,模型计算结果如图5 所示.

图4 含裂纹缺陷拉伸试件尺寸及网格划分示意图 (a) 试件结构及尺寸;(b) 试件网格划分Fig.4.Shape,sizes and finite element meshing of the specimen with crack defect:(a) Shape and sizes of the specimen;(b) finite element meshing of the specimen.

由图5 可知,不同提离高度下磁场水平分量Hx与法向分量Hz变化规律为:Hx在缺陷中心处出现极大值,在缺陷左右边缘出现两处较小谷值点;而Hz在缺陷中心过零点,在缺陷左右边缘出现正负峰-谷值;随着提离高度的增大,Hx与Hz的幅值迅速减小.上述规律与实验结果变化规律一致,说明本文模型能够正确反映金属磁记忆检测信号的变化规律.

图5 不同提离高度条件下试件表面 Hx与 Hz 计算 结果(a) Hx;(b) HzFig.5.Calculation of Hxand Hz with different lift off:(a) Hx;(b) Hz .

进一步地,用Maciej 和Gawrilenko[21]在含圆孔型缺陷的拉伸试样上开展的实验结果进行对比验证,他们实验中的拉伸试样结构尺寸如图6 所示.

图6 文献[21]中含圆孔缺陷拉伸试样结构及尺寸示意图Fig.6.Shape and sizes of the specimen with hole defect in Ref.[21].

实验时,试件所受拉伸载荷为50 MPa,测试如图6 中紫色虚线框所示范围内试件表面的三个磁场分量分布情况,文献[21]中的测试结果如图7(a)—(c)所示,本文正演模型的理论计算结果如图7(d)—(f)所示.

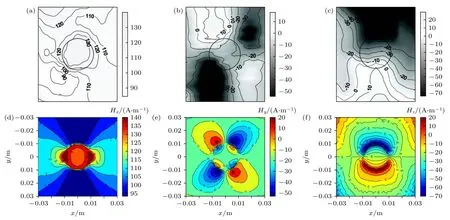
图7 含圆孔缺陷拉伸试样表面磁场分布理论计算结果与实验结果对比 (a)实验测试的 Hx分布情况;(b) 实验测试的 Hy 分布情况;(c) 实验测试的 Hz分布情况;(d) 理论计算的 Hx分布情况;(e) 理论计算的 Hy分布情况;(f) 理论计算的 Hz 分布情况Fig.7.Comparison between theoretical results and experimental results of magnetic field distribution of the specimen with hole defect:(a) Hxof experimental results;(b) Hyof experimental results;(c) Hzof experimental results;(d) Hx of theoretical results;(e) Hyof theoretical results;(f) Hz of theoretical results.

由实验结果可知:含圆孔缺陷试件在拉伸载荷作用下,水平分量Hx在圆孔缺陷中心区域出现峰值,峰值区域轮廓与圆孔轮廓接近,Hx峰值在130 A/m 以上;切向分量Hy在圆孔缺陷的4 个角点位置出现正、负峰-谷值区域,第2 和第4 象限的正向峰值在10 A/m 以上,第1 和第3 象限内的负向谷值在–50 A/m 以下;法向分量Hz在圆孔上、下边缘两侧出现正、负峰-谷值变化,在圆孔中心过零点,Hz正向峰值在20 A/m 以上,负向谷值约在–70 A/m 以下.

如表1 所列,将本文模型和文献[13]图3.9 中理论模型计算结果与实验结果对比可以发现:不同理论模型的计算结果均能反映试件表面磁场三个分量的分布规律,但是磁场各分量的等值线分布和数值存在一定的差异,本文磁荷模型计算得到的Hx幅值范围是70—140 A/m,Hy幅值范围是–50—20 A/m,Hz幅值范围是–60—20 A/m;文献[13]图3.9 中Hx幅值范围是80—140 A/m,Hy幅值范围是–40—10 A/m,Hz幅值范围是–70—20 A/m.因此,在数值上两种模型计算结果均能很好反映实验结果,但本文正演模型计算得到的磁场各分量的等值线分布更接近实验分布结果.

进一步地,用Maciej 等[22]在含裂纹缺陷的S235 钢(相当于我国Q235 钢)拉伸试样上开展的实验进行验证,他们实验中的含裂纹缺陷的拉伸试样结构尺寸如图8 所示.

实验中,先在试件两端施加225 MPa 的拉伸载荷,卸载后测试如图8 中紫色虚线框所示范围内的磁场分量分布情况,文献[22]中实验结果如图9(a)—(c)所示,本文模型的理论预测结果如图9(d)—(f)所示.

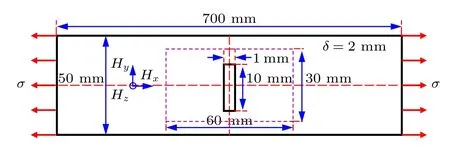
图8 文献[22]中裂纹缺陷拉伸试样示意图Fig.8.Shape and sizes of the specimen with crack defect in Ref.[22].

根据图9(a)—(c)所示实验结果可知:含裂纹缺陷试样在拉伸载荷作用下,水平分量Hx在裂纹缺陷中心区域出现峰值区域,在缺陷左右边缘位置出现谷值区域,峰值区域轮廓与裂纹轮廓基本一致,Hx幅值范围约为100—160 A/m;切向分量Hy在裂纹缺陷的4 个角点位置出现正、负峰—谷值区域,在第1 和第3 象限的正向峰值约为10 A/m,在第2 和第4 象限内的负向谷值约为–40 A/m;法向分量Hz裂纹的左、右边缘出现正、负峰—谷值变化,在裂纹中心过零点,Hz的幅值范围为–60—80 A/m.

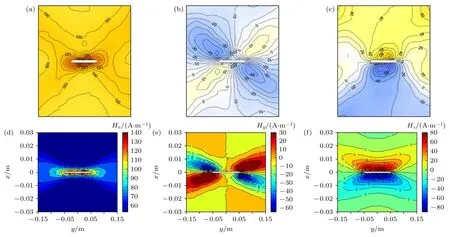
图9 含裂纹缺陷拉伸试样表面磁场分布理论计算结果与实验结果对比 (a) 实验测试的 Hx分布情况;(b) 实验测试的 Hy 分布情况;(c) 实验测试的 Hz分布情况;(d) 理论计算的 Hx分布情况;(e) 理论计算的 Hy分布情况;(f) 理论计算的 Hz 分布情况Fig.9.Comparison between theoretical results and experimental results of magnetic field distribution of the specimen with crack defect:(a) Hxof experimental results;(b) Hyof experimental results;(c) Hzof experimental results;(d) Hx of theoretical results;(e) Hyof theoretical results;(f) Hz of theoretical results.

如表2 所列,将本文模型和文献[13]图3.28中理论模型计算结果与文献[22]中实验结果对比可以发现:本文建立的磁荷模型能够反映实验测试得到的磁场分布规律,且计算值与实验测试结果较为接近,磁荷模型计算得到的水平分量Hx幅值范围 为60—140 A/m,切向分量Hy幅值范围为–60—30 A/m,法向分量幅值范围为–80—80 A/m.出现数值差异的主要原因可能在于:在实际检测过程中,测试结果不可避免地会受到环境干扰磁场的影响,而在理论计算过程中没有考虑环境干扰磁场的影响.文献[13]图3.28 中水平分量Hx幅值范围为–400 —400 A/m,切向分量Hy幅值范围为–200—200 A/m,法向分量的幅值范围为–500—500 A/m,磁场各分量的等值线分布和数值与实验结果存在显著差异.因此,本文模型能更好反映裂纹缺陷表面磁场各分量的分布规律.

表2 不同正演模型计算含裂纹缺陷试件结果与实验测试结果对比Table 2.Comparison of magnetic field distribution of specimen with crack defect calculated by different models.

4.2 模型讨论

4.2.1 应力集中与宏观裂纹磁记忆信号对比

将应力集中区域简化为与图4(a)中裂纹形状相同的矩形区域,应力集中区域长8 mm、宽2 mm、深2 mm,在此区域应力为200 MPa,其他区域应力为50 MPa;含裂纹缺陷试件的裂纹缺陷长、宽、深分别为8 mm,2 mm 和2 mm,试件所受拉伸载荷为50 MPa.计算后提取试件中心距离试件表面1 mm,20 mm×20 mm 区域内的磁场分布情况,结果如图10 所示.

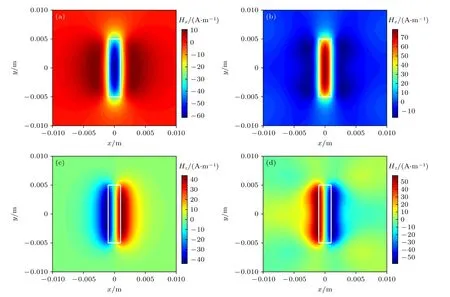
图10 应力集中与宏观裂纹缺陷对试件表面磁场分布的影响对比 (a) 应力集中区域 Hx分布情况;(b) 宏观裂纹缺陷 Hx 分布情况;(c) 应力集中区域 Hz分布情况;(d) 宏观裂纹缺陷 Hz 分布情况Fig.10.Comparison of effects of stress concentration and macroscopic crack defect on the distribution of magnetic field distribution:(a) Hxof stress concentration;(b) Hxof macroscopic crack defects;(c) Hzof stress concentration;(d) Hz of macroscopic crack defects.

由图10 可知,应力集中与宏观裂纹对磁记忆信号分布的影响明显不同:当试件内部只存在应力集中、尚未形成宏观缺陷时,Hx在应力集中区域出现负向谷值,在应力集中区域的左右边缘位置出现两个幅值较小的正向峰值,其幅值范围约为–60—10 A/m;Hz在应力集中区域的左右两侧分别出现正、负峰-谷值变化,其中应力集中区域左侧为负向谷值区域,右侧为正向峰值区域,其幅值范围约为–40—40 A/m.当试件出现宏观缺陷后,试件表面磁场各分量分布规律将发生反转:Hx在缺陷中心位置处出现正向峰值区域,而在缺陷左右边缘位置出现两个幅值较小的负向谷值区域,其幅值范围约为–10—70 A/m;Hz在裂纹缺陷的左侧为正向峰值区域,右侧为负向谷值区域,其幅值范围约为–60—60 A/m.

进一步分析含裂纹缺陷试件在50,100,150,和200 MPa 四种应力状态下磁场分布规律,结果如图11 所示.

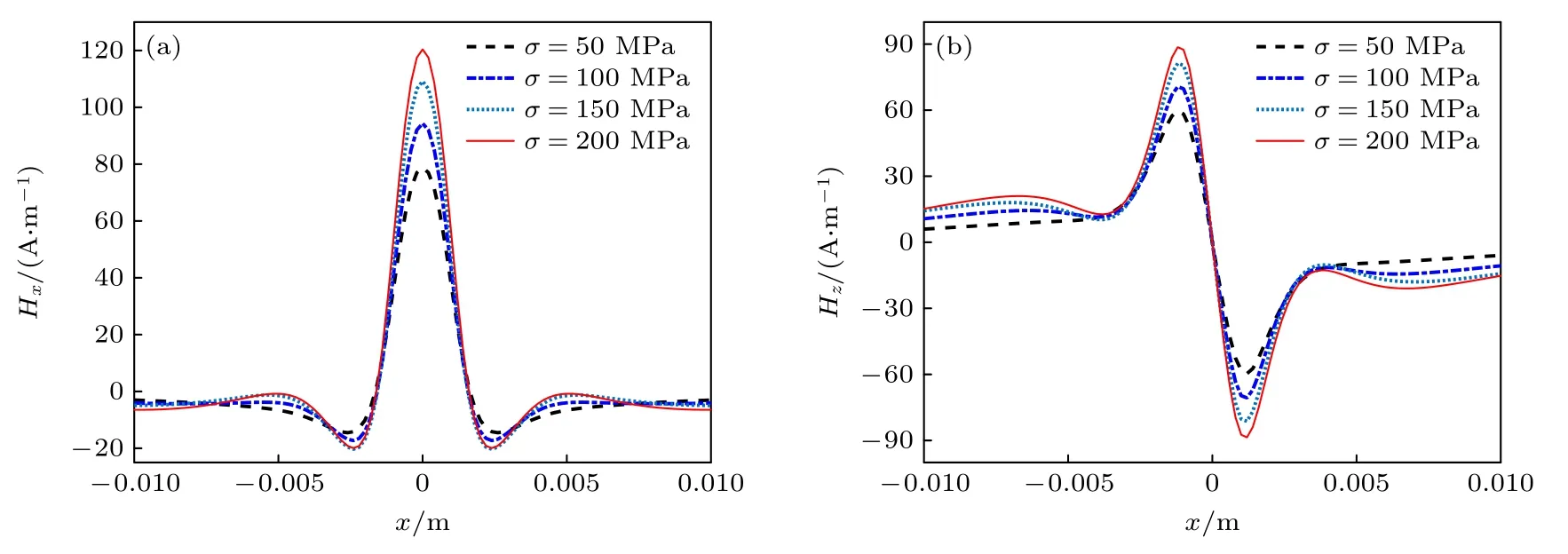
图11 应力对裂纹缺陷试件表面 Hx与 Hz的影响 (a) 应力对裂纹缺陷试件表面 Hx的影响;(b) 应力对裂纹缺陷试件表面Hz的影响Fig.11.Influence of stress on Hxand Hzof the specimen with macroscopic crack defect:(a) Influence of stress on Hx ;(b) influence of stress on Hz .

不同应力状态下,试件表面磁场各分量的分布规律基本一致:在缺陷位置磁场水平分量出现峰值,法向分量过零点,并出现峰谷值变化,说明当试件出现宏观缺陷后,试件表面的磁场信号曲线形状主要取决于宏观缺陷的轮廓形状,而应力幅值的影响相对较小;应力幅值主要影响磁场分量的幅值:在裂纹缺陷中心处,Hx由50 MPa 时的78.83 A/m 增大到了200 MPa 时的120.4 A/m,而Hz由50 MPa 时的58.23 A/m 增大至200 MPa 时的88.61 A/m 左右.

4.2.2 裂纹缺陷参数对磁记忆信号的影响

以裂纹缺陷为例,分析缺陷尺寸参数对磁记忆信号的影响规律,建立如图4(a)所示的含缺陷试件,尺寸参数包括:宽度Wc、长度Lc、深度Dc和埋深Bc.在总结金属磁记忆信号各分量特征参数基础上,选择与磁场水平分量Hx和法向分量Hz相关的特征参数如图12 所示.

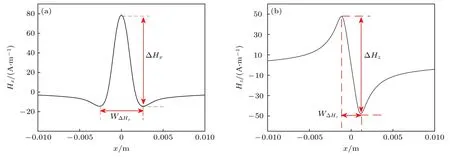
图12 磁记忆检测信号特征参数 (a) 与磁场水平分量 Hx相关的特征值;(b) 磁场法向分量 Hz 相关的特征值Fig.12.Characteristic parameters of magnetic memory detection signal:(a) Characteristic parameters of Hx ;(b) characteristic parameters of Hz .

其中,ΔHx表示磁场水平分量Hx缺陷中心峰值及左右缺陷两侧谷值之差;ΔHz表示磁场法向分量Hz缺陷左右两侧正、负峰谷值之差;WΔHx表示磁场水平分量Hx在缺陷左右两侧谷值之间的距离;WΔHz表示磁场法向分量Hz在缺陷左右两侧正、负峰谷值之间的距离.

1)缺陷宽度对磁场分布的影响

缺陷宽度Wc分别取0.5,1,1.5,2,3,4,5 和6 mm,缺陷长度Lc为10 mm,深度Dc为2 mm,缺陷埋深Bc为0,试件所受拉伸载荷为50 MPa,提取试件中部–10 —10 mm、距离试件表面1 mm 高度位置处Hx和Hz,计算各分量的特征参数,结果如图13 所示.

图13 槽形 缺陷 宽度 Wc对 磁场 分布的影响 (a) Hx随缺陷宽度 Wc变化情况;(b) Hz随 缺陷 宽度 Wc变 化情 况;(c) ΔHx 和ΔHz随缺陷宽度 Wc变化情 况;(d) 和 随缺陷宽度 Wc 变化情 况Fig.13.Influence of crack defect width Wcon magnetic field distribution:(a) Variation of Hxwith Wc;(b) variation of Hz with Wc;(c) variation of ΔHxand ΔHzwith Wc;(d) variation of and with Wc .

由图13(a)和图13(b)可知:在缺陷中部,磁场水平分量Hx曲线出现正向峰值,随着缺陷宽度的增大,Hx曲线的异常区域变宽,在中部出现平台区域,且Hx的峰值呈现出先增大后减小的趋势;而磁场法向分量Hz曲线出现正、负峰-谷值变化,并在缺陷中心位置过零点,随着缺陷宽度的增大,Hz异常区域宽度和峰-谷值的幅值都逐渐增大.由图13(c)可知:当缺陷宽度小于3 mm 时,ΔHx随缺陷宽度的增大而增大,当缺陷宽度超过3 mm 后,ΔHx发生反转,小幅减小后逐渐趋于平稳;与 ΔHx不同,ΔHz则随缺陷宽度的增大呈非线性增大趋势,且在缺陷宽度较小时,增大的趋势更为明显,而当缺陷宽度超过3 mm 后,ΔHz增大趋势明显放缓.由图13(d)可知:WΔHx和WΔHz随缺陷宽度的增大呈线性增大趋势,不同缺陷宽度Wc下,WΔHx的值均比缺陷实际宽度偏大;当缺陷宽度小于3 mm时,WΔHz的值比缺陷实际宽度偏大,当缺陷宽度大于3 mm 后,WΔHz的取值就十分接近缺陷的实际宽度.

2)缺陷长度对磁场分布的影响

缺陷宽度Wc为1 mm,深度Dc为2 mm,缺陷长度Lc分别取1,2,3,4,5,6,8 和10 mm,试件所受拉伸载荷为50 MPa,提取试件中部–10—10 mm、距离试件表面1 mm 高度位置处Hx和Hz,计算分量的特征参数,结果如图14 所示.

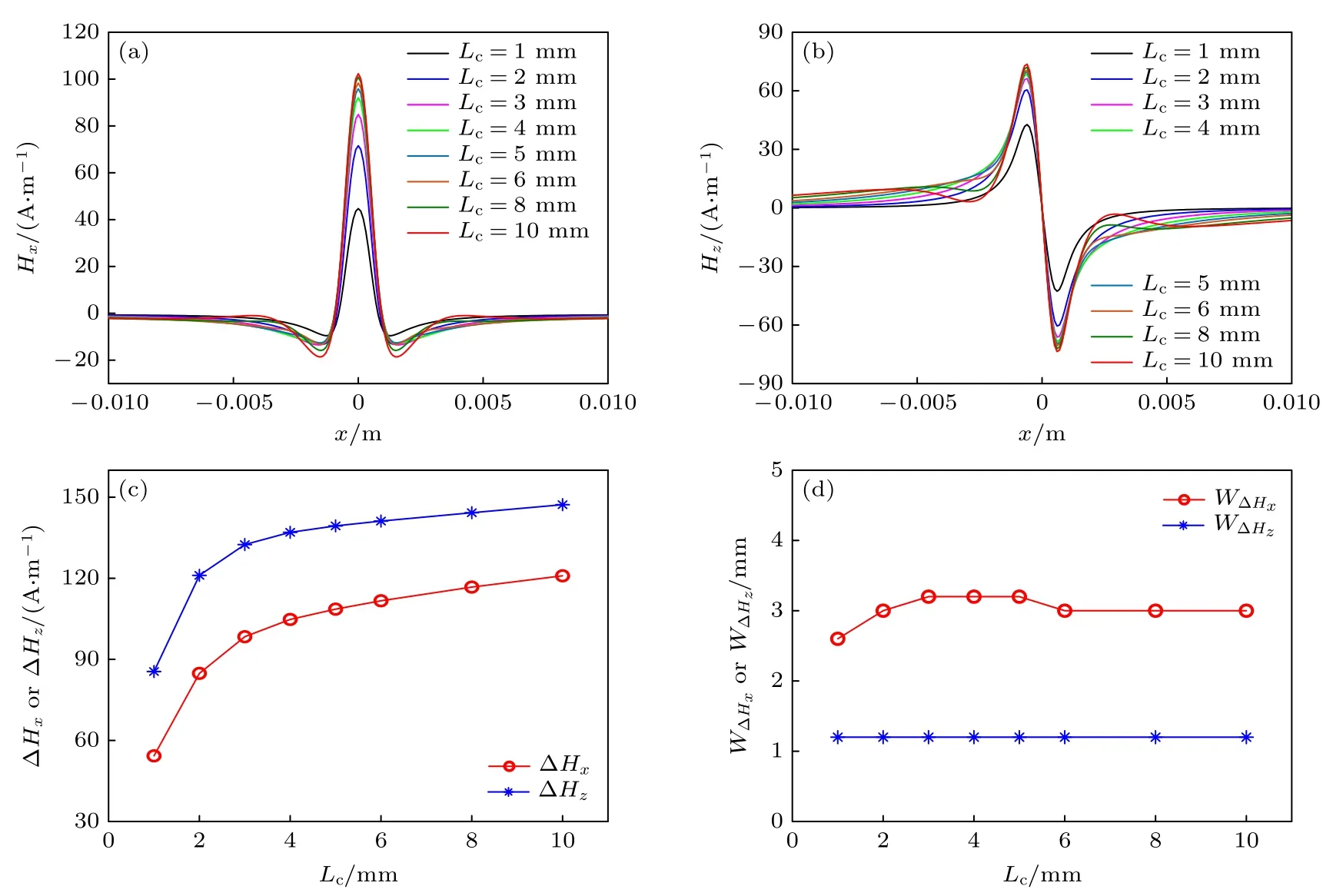
图14 槽形缺陷长度 Lc对 磁场分布的影响 (a) Hx随缺陷长度 Lc变化情况;(b) Hz随缺陷长度 Lc变化情况;(c) ΔHx 和ΔHz随缺陷长度 Lc变化情况;(d) 和 随缺陷长度 Lc 变化情况Fig.14.Influence of crack defect lengthen Lcon magnetic field distribution:(a) Variation of Hxwith Lc;(b) variation of Hz with Lc;(c) variation of ΔHxand ΔHzwith Lc;(d) variation of and with Lc.

由图14 可知:随着缺陷长度的增大,磁场水平分量Hx和法向分量Hz呈非线性增大趋势,当缺陷长度Lc小于4 mm 时,ΔHx和 ΔHz随缺陷长度Lc的增大快速增大,当缺陷长度Lc超过4 mm 后,ΔHx和 ΔHz的增大趋势逐渐减缓,相同缺陷长度Lc条件下 ΔHz幅值大于 ΔHx幅值;和几乎不随缺陷长度的变化而变化,可见缺陷长度Lc对异常区域宽度的影响较小.

3)缺陷深度对磁场分布的影响

缺陷深度Dc分别取0.5,1,1.5,2,2.5,3,3.5和4 mm,Lc为10 mm,Wc为2 mm,试件厚度为4 mm,所受拉伸载荷为50 MPa,提取试件中部–10—10 mm、距离试件表面1 mm 高度处Hx和Hz,计算分量特征参数,结果如图15 所示.

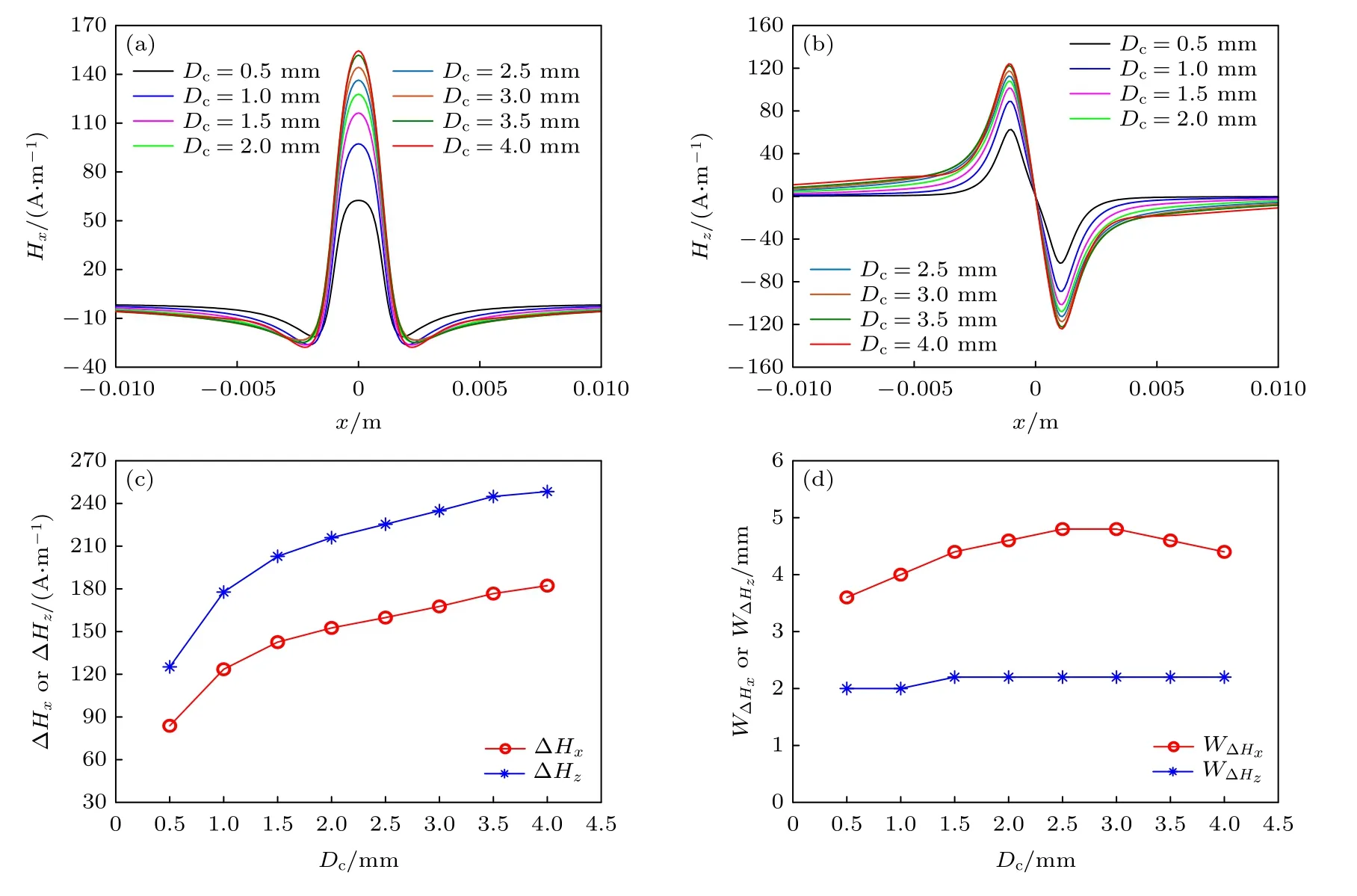
图15 槽形缺陷深度 Dc对磁场分布的影响 (a) Hx随 缺陷深度 Dc变化情况;(b) Hz随缺陷深 度 Dc变化情况;(c) ΔHx 和ΔHz随缺陷深度 Dc变 化情况;(d) 和 随缺陷深度 Dc 变化情况Fig.15.Influence of crack defect depth Dcon magnetic field distribution:(a) Variation of Hxwith Dc;(b) variation of Hz with Dc;(c) variation of ΔHxand ΔHzwith Dc;(d) variations of and with Dc .

由图15 可知:随着缺陷深度Dc的增大,磁场水平分量Hx和法向分量Hz幅值都呈非线性增大的趋势,且当缺陷深度Dc较小时,水平分量Hx的峰值区域较宽,随着缺陷深度Dc的增大,Hx的峰值区域收窄;同时,随着缺陷深度Dc的增大,磁场水平分量Hx异常区域宽度呈小幅增大,而法向分量Hz的峰谷值间距几乎不随缺陷深度Dc的变化而变化,由此可见缺陷深度Dc对异常区域宽度的影响较小.

4)缺陷埋深对磁场分布的影响

拉伸试件的厚度增加为4 mm,缺陷长度Lc为10 mm,宽度Wc为2 mm,缺陷深度Dc为1 mm,缺陷埋深Bc分别取0,0.5,1,1.5,2 和2.5 mm,试件所受拉伸载荷为50 MPa,提取试件中部–10—10 mm、距离试件表面1 mm 高度位置处Hx和Hz,并计算各分量的特征参数,结果如图16 所示.

由图16 可知:随着缺陷埋深Bc增大,磁场水平分量Hx和法向分量Hz幅值都呈非线性减小的趋势,当缺陷埋深Bc小于1.5 mm 时,随着缺陷埋深Bc的增大,Hx和Hz的峰值均迅速衰减,当缺陷埋深Bc超过1.5 mm 后,Hx和Hz的波峰、波谷逐渐变得不明显;同时,随着缺陷埋深Bc的增大,磁场水平分量Hx和法向分量Hz异常区域宽度和均逐渐增大.

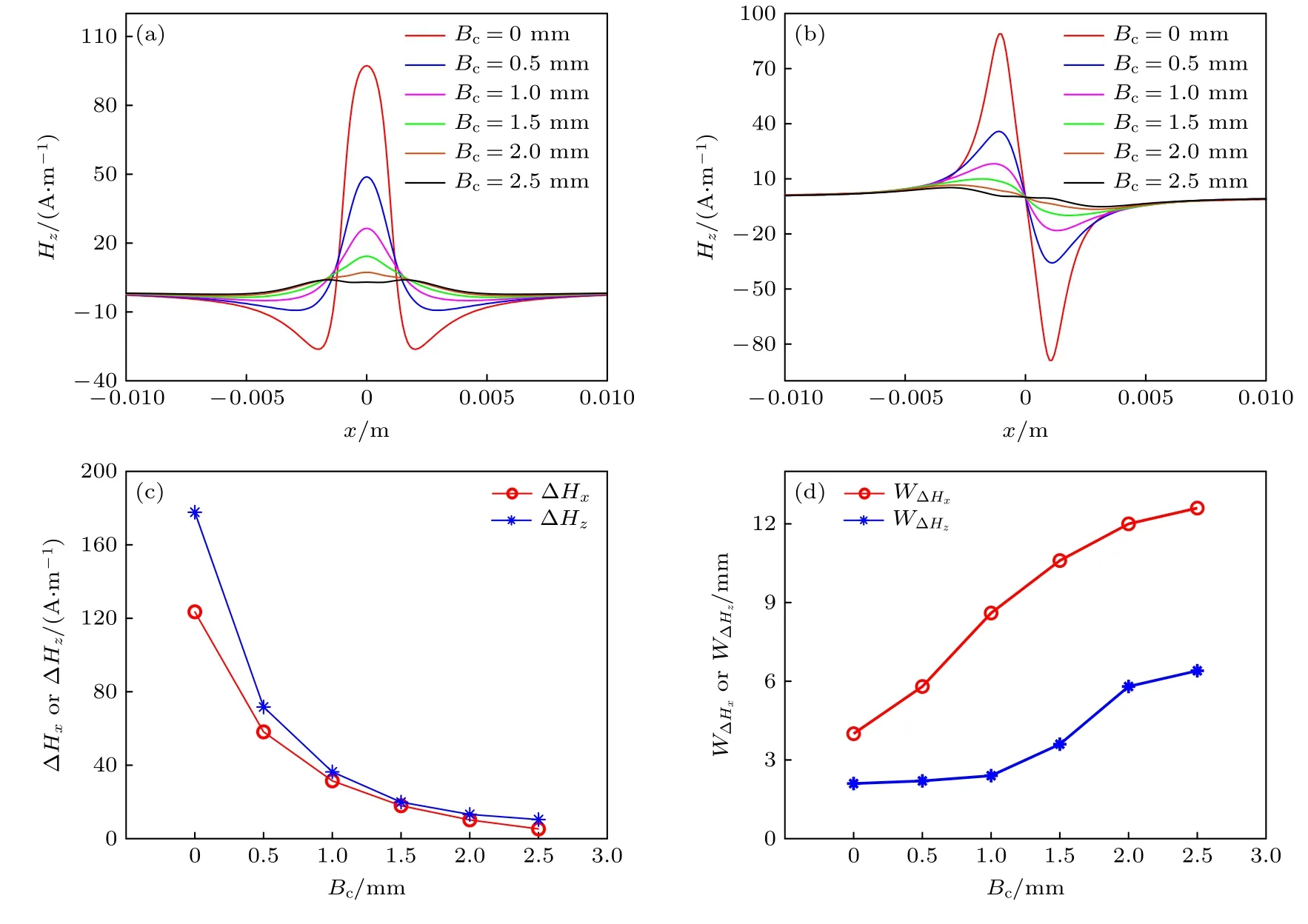
图16 槽形缺陷埋深 Bc对 磁场分布的影响 (a) Hx随缺陷埋深 Bc变化情况;(b) Hz随缺陷埋深 Bc变化情况;(c) ΔHx 和ΔHz随缺陷埋深 Bc变化情况;(d) 和 随缺陷埋深 Bc 变化情况Fig.16.Influence of crack defect buried depth Bcon magnetic field distribution:(a) Variation of Hxwith Bc;(b) variation of Hz with Bc;(c) variation of ΔHxand ΔHzwith Bc;(d) variation of and with Bc .

5 结论

1)针对现有磁记忆检测磁偶极子正演模型存在的问题,本文在结合力磁耦合理论、磁荷理论和有限元方法基础上,将试件离散为有限多个微小单元,假设每个微小单元内部磁特征参数分布均匀,确定了单元应力、磁化强度与磁荷密度之间的关系,建立了能够考虑应力不均匀分布对磁荷密度分布影响的金属磁记忆检测正演模型.通过与实验结果对比,本文建立模型无论是定性、还是定量上都能很好预测磁记忆信号变化规律,可为定量分析磁记忆检测过程中缺陷附近磁场变化规律提供新的理论模型.

2)应力集中和宏观缺陷对构件表面磁场分布的影响具有显著区别:当试件内部只存在应力集中时,水平分量Hx在应力集中区域出现负向谷值区域,法向分量Hz在应力集中区域出现由负到正的谷-峰值变化;当试件出现宏观缺陷后,磁场各分量的分布规律与只存在应力集中时的分布正好相反,可以利用磁场信号的分布特征对试件内部的损伤类型进行判断;此外,当试件出现宏观缺陷后,试件表面的磁场信号曲线形状主要取决于宏观缺陷的轮廓形状,而应力幅值的影响相对较小.

3)以裂纹缺陷为例,详细讨论了裂纹缺陷宽度Wc、长度Lc、深度Dc和埋深Bc对磁记忆信号及其特征参量的影响规律.结果表明:,与缺陷宽度Wc之间存在较好的线性对应关系;ΔHx,ΔHz随缺陷长度Lc和深度Dc的增大而增大;ΔHx,ΔHz随缺陷埋深Bc的增大而逐渐减小.