随机路面下轮毂电机偏心对电动汽车平顺性影响
李 杰, 贾长旺, 成林海, 赵 旗
(吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130025)
随着国内外对于新能源汽车的重视,加之大数据、智能网联、5G通信、辅助驾驶和车用传感器技术的快速发展,汽车行业迎来巨大的变革.电动汽车作为以上技术发展连接点和重要一环,引起了传统汽车厂商、新型造车势力、互联网技术公司和消费群体的广泛关注[1-4].
轮毂电机电动汽车具有节能高效、环境友好、结构紧凑和对单个车轮可以独立控制等优点,正在成为新能源汽车的一个研究热点[5-7].
相较于传统汽车和集中驱动电动汽车,轮毂电机电动汽车直接将电机集成于车轮内,使得非簧载质量增加,对电动汽车平顺性造成直接影响.为了改善轮毂电机对电动汽车平顺性造成的影响,在不改变悬架构型的情况下,已经从电机轻量化[8]和引入动力吸振结构[9]等方面开展了相应的研究工作.
然而,以往研究较少考虑轮毂电机偏心对电动汽车平顺性的影响.事实上,制造或者装配都可能造成轮毂电机偏心,即使在制造或装配过程不存在电机偏心,轮毂电机使用磨损也会造成电机偏心.因此,研究电机偏心对轮毂电机电动汽车平顺性的影响具有理论研究价值和实际应用意义.
针对上述问题,在前人研究的基础上,本文开展轮毂电机电动汽车振动模型、路面激励和轮毂电机激励、轮毂电机偏心对平顺性影响的研究,完成从理论分析、程序开发到仿真实现的全部过程,为轮毂电机电动汽车平顺性的改善、优化和控制奠定前期工作基础.
1 轮毂电机电动汽车振动模型
1.1 模型描述
在传统汽车平面4自由度振动模型基础上[10],在前后轴非簧载质量中引入轮毂电机质量,增加电机激励,建立轮毂电机电动汽车平面4自由度振动模型,如图1所示.
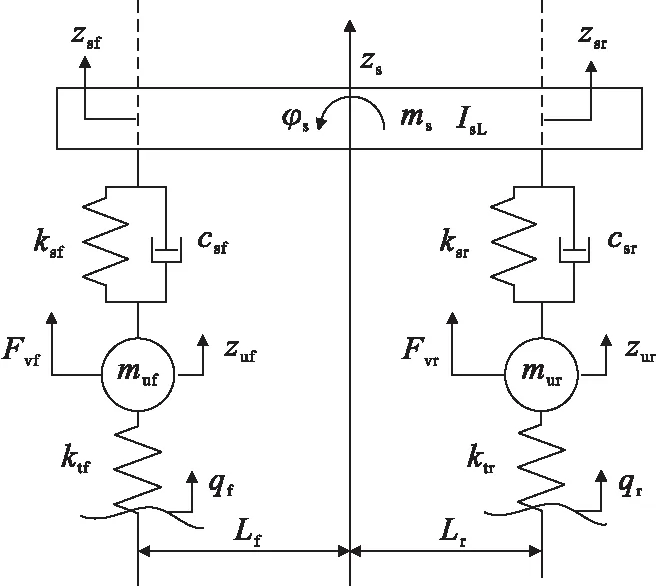
图1 轮毂电机电动汽车平面4自由度振动模型
在图1中,ms和IsL为车身质量和车身俯仰转动惯量,kg和kg·m2;muf和mur为包含轮毂电机的前轴和后轴的非簧载质量,kg;ksf和ksr为前轴和后轴的悬架刚度,N/m;ktf和ktr为前轴和后轴的轮胎刚度,N/m;csf和csr为前轴和后轴的悬架阻尼,N·s/m;Lf和Lr为车身质心与前轴和后轴的距离,m;Fvf和Fvr为前轴和后轴的轮毂电机激励,N;qf和qr为前轮和后轮的路面激励,m;zs和φs为车身的垂向位移和俯仰角位移,m和rad;zsf和zsr为前轴和后轴的悬架与车身连接点垂向位移,m;zuf和zur为前轴和后轴的非簧载质量垂向位移,m.
1.2 状态方程
基于Lagrange方程,针对zsf,zsr,zuf和zur分别建立如下微分方程:
(1)
(2)
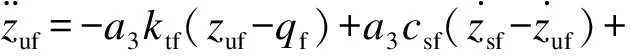
(3)
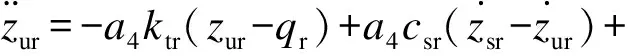
(4)
其中:
联立式(1)~式(4),得到状态方程:
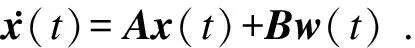
(5)
其中:
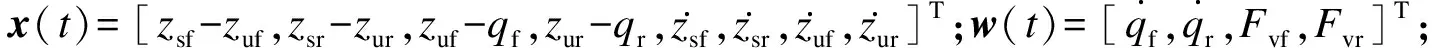
A=
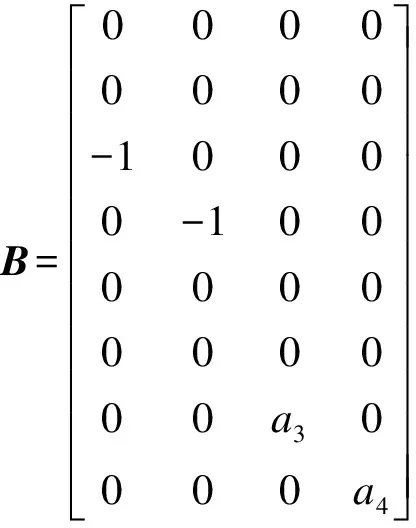
1.3 输出向量
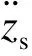
y(t)=Cx(t) .
(6)
其中:
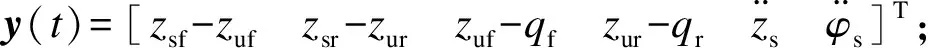
前轮胎和后轮胎的动载荷Fdf和Fdr为
(7)
由静态平衡关系可知,前轮胎和后轮胎的静载荷Gf和Gr为
(8)
式中,g为重力加速度,m/s2.
1.4 评价指标
为了保证电动汽车平顺性,取如下响应作为振动响应量:
2) 前悬架动行程zuf-qf和后悬架动行程zur-qr;
3) 前轮胎相对动载Fdf/Gf和后轮胎相对动载Fdr/Gr.
在随机路面下,平顺性评价指标由各个振动响应量的均方根值表示[11],即
(9)
式中:x为振动响应量的均方根值;xi为振动响应量各个时刻的值;n为采样点个数.
2 随机路面激励和轮毂电机激励
2.1 随机路面前轮激励
由滤波白噪声方法建立随机路面前轮激励qf(t)为[12]
(10)
式中:W(t)为理想单位白噪声,其均值为0和功率密度为1;u为车速,m/s;nq=0.000 1为截止空间频率,m-1;n0=0.1为参考空间频率,m-1;Gq(n0)为空间参考频率n0的路面不平度系数,值由路面标准决定[11].
2.2 随机路面后轮激励
当车辆在道路上直线行驶时,假设随机路面前后轮激励输入是相同的[11],并且随机路面后轮激励与随机路面前轮激励只是存在一个时间的滞后τ,即
qr(t)=qf(t-τ) .
(11)
式中,qr(t)为随机路面后轮激励,m.
滞后时间τ为车辆轴距L与车速u的比值:
(12)
对式(11)进行Laplace变换,有
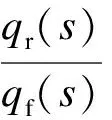
(13)
式中:qf(s)为随机路面前轮激励qf(t)的Laplace变换,m;qr(s)为随机路面后轮激励qr(t)的Laplace变换,m.
对式(13)的右端项,采用4阶对称Pade逼近,再通过Laplace逆变换得到qr(t)和qf(t)的关系[13],有
(14)
其中:
2.3 轮毂电机激励
轮毂电机主要有永磁同步电机、开关磁阻电机、异步电机和横向磁场电机等[14].开关磁阻电机具有简单可靠、运行效率高等优点,但其转矩波动较大、振动噪声大.因此,选择开关磁阻电机作为研究对象[15].典型的四相8/6极开关磁阻电机及其一组开关电路,如图2所示.在对电机进行一定的假设条件下,某一时刻下电机整体垂向激励为单相转子垂向力之和[16],即
Fv=Fva+Fvb+Fvc+Fva′+Fvb′+Fvc′.
(15)
式中:Fva,Fva′,Fvb,Fvb′,Fvc和Fvc′分别为单相转子的垂向力,N;a和a′,b和b′,c和c′为轮毂电机中对应的转子.
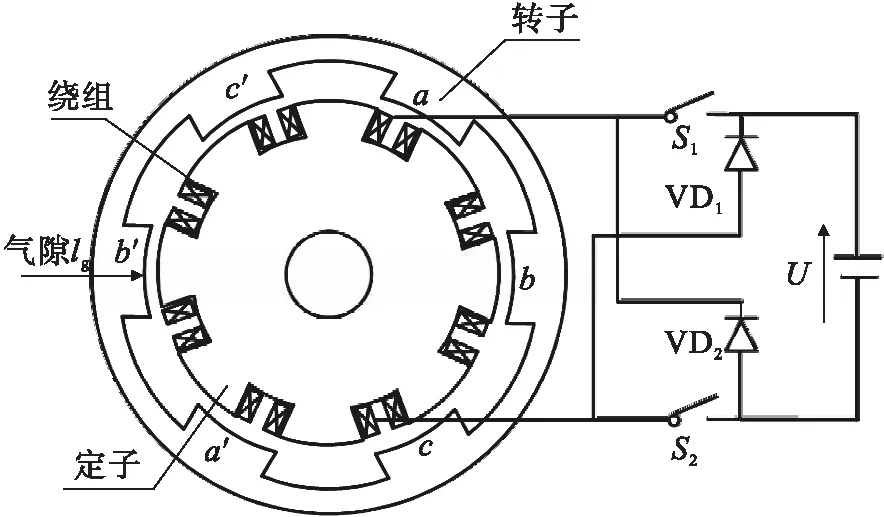
图2 四相8/6极开关磁阻电机结构
单相转子的垂向力为[13]
(16)
其中:j=a,b,c,a′,b′,c′;
B=Ki2/(2R);θ=θint+ωt+φ;b=(R-r)-ecosφ.
式中:i为电机电流,A;Lmin为最小电感,H;b为电机气隙,m;e为定子和转子的偏心距,m;K为电感上升斜率,H/rad;R为转子内半径,m;r为定子外半径,m;TR为单相转子转动周期,s;ω为电机转动角速度,rad/s;θint为各相转子初始位置,rad;φ为各定子绕组的相位角,rad.
3 轮毂电机偏心对平顺性的影响
3.1 随机路面激励仿真
基于随机路面激励的描述,开发了随机路面前轮和后轮的激励Matlab/Simulink仿真模型.其中,白噪声序列使用Simulink的【Band-Limited White Noise】模块生成,采用Runge-Kutta方法求解式(10)和式(14).
选取路面等级为B级路面,取所研究电动汽车的轴距为2.76 m,车速为40 km/h,仿真时间为20 s,步长为0.001 s.随机路面前轮和后轮的激励,如图3所示.
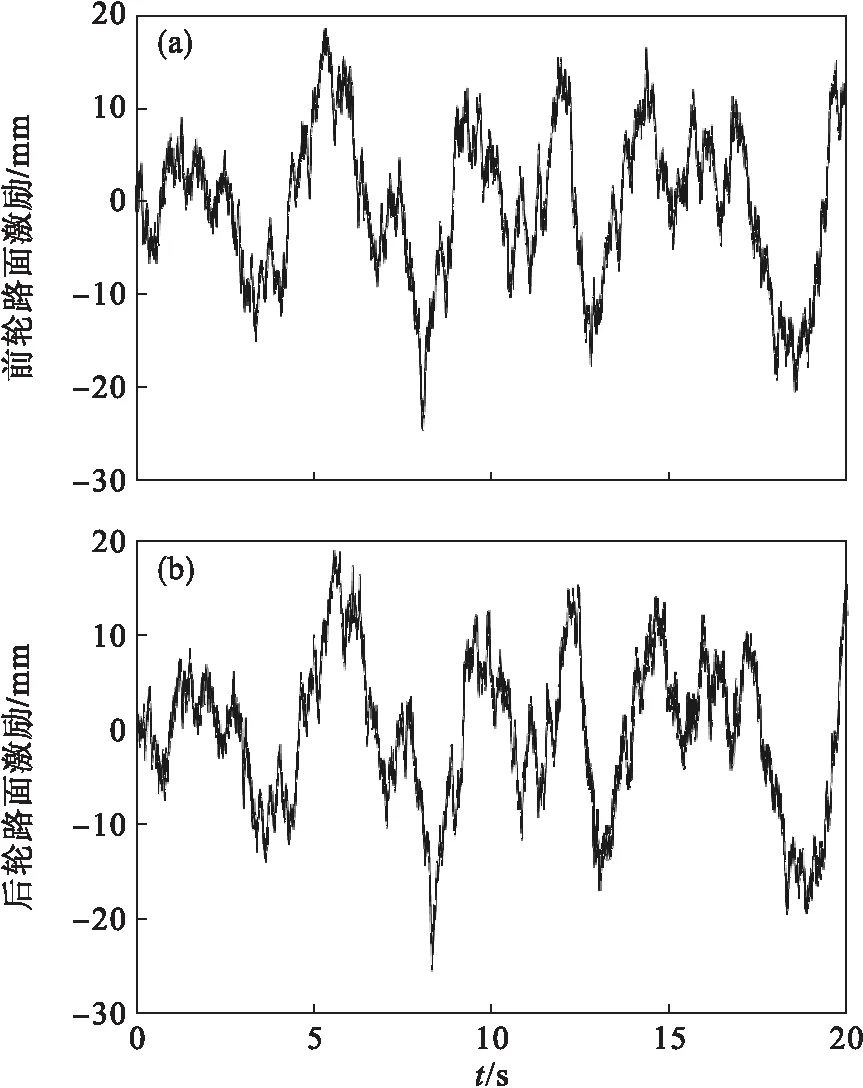
图3 B级路面前轮和后轮的激励
由图3可知,本文所建立的前轮和后轮的B级随机路面激励是随机变化的,符合随机路面激励变化规律.
3.2 轮毂电机激励仿真
基于轮毂电机激励的描述,开发了开关磁阻电机激励Matlab/Simulink仿真模型.
设偏心距e=(R-r)·er,其中er是以百分率表示的偏心率.分别取er=0和er=10 %两种情况,前者对应于电机无偏心情况,后者对应于电机偏心情况,取某开关磁阻电机参数[13],两种情况的电机偏心激励,如图4所示.
由图4可知,当电机不存在偏心时,由于各处气隙相同,电机垂向激励几乎为零,即电机不存在垂向激励;当电机转子和定子存在偏心时,由于各处气隙不同,电机产生单一方向的垂向激励.所以,在理想情况下,电机定子和转子圆心重合不存在偏心,即e=0.在电机使用过程中,由于磨损等原因,使得定子和转子产生偏心,即e≠0,造成气隙变化,导致电机产生不平衡的电机垂向激励.
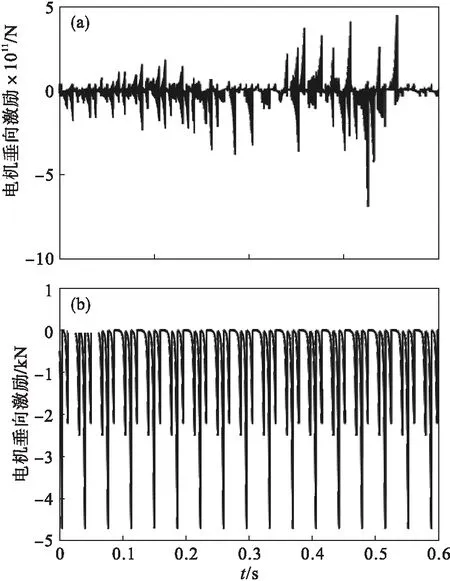
图4 两种情况的轮毂电机偏心激励
3.3 平顺性仿真
基于轮毂电机电动汽车振动模型,开发了轮毂电机电动汽车平顺性Matlab/Simulink仿真模型.
在B级路面上,采用某轮毂电机电动汽车参数,设定如下4种情况:
1) 前后轮无偏心,简称无偏心;
2) 前轮偏心而后轮无偏心,简称前轮偏心;
3) 前轮无偏心而后轮偏心,简称后轮偏心;
4) 前后轮偏心,简称双轮偏心.
在车速60 km/h时,针对上述4种情况进行仿真,可得到4种情况的车身垂向加速度、车身俯仰角加速度、前悬架动行程、后悬架动行程、前轮胎相对动载和后轮胎相对动载的时间历程.车身垂向加速度、前悬架动行程和前轮胎相对动载的无偏心与双轮偏心的结果对比,车身俯仰角加速度、后悬架动行程和后轮胎相对动载的前轮偏心与后轮偏心的结果对比,如图5所示.
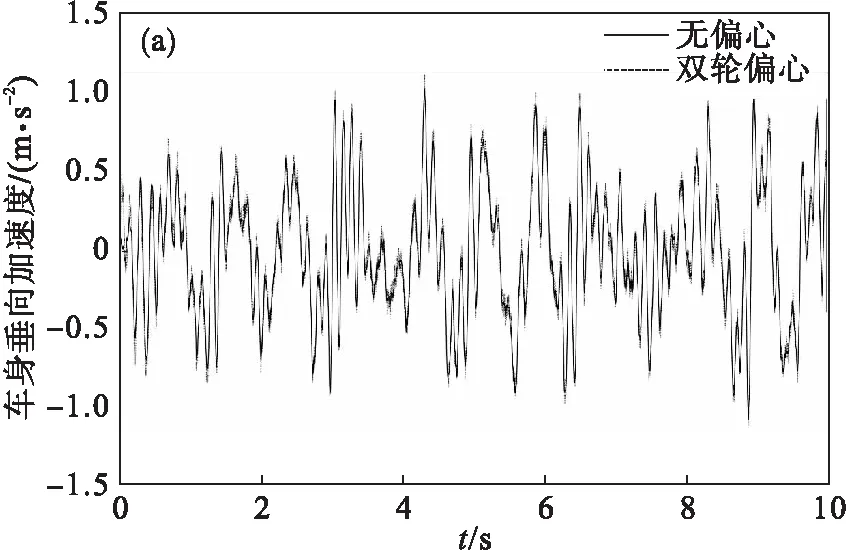
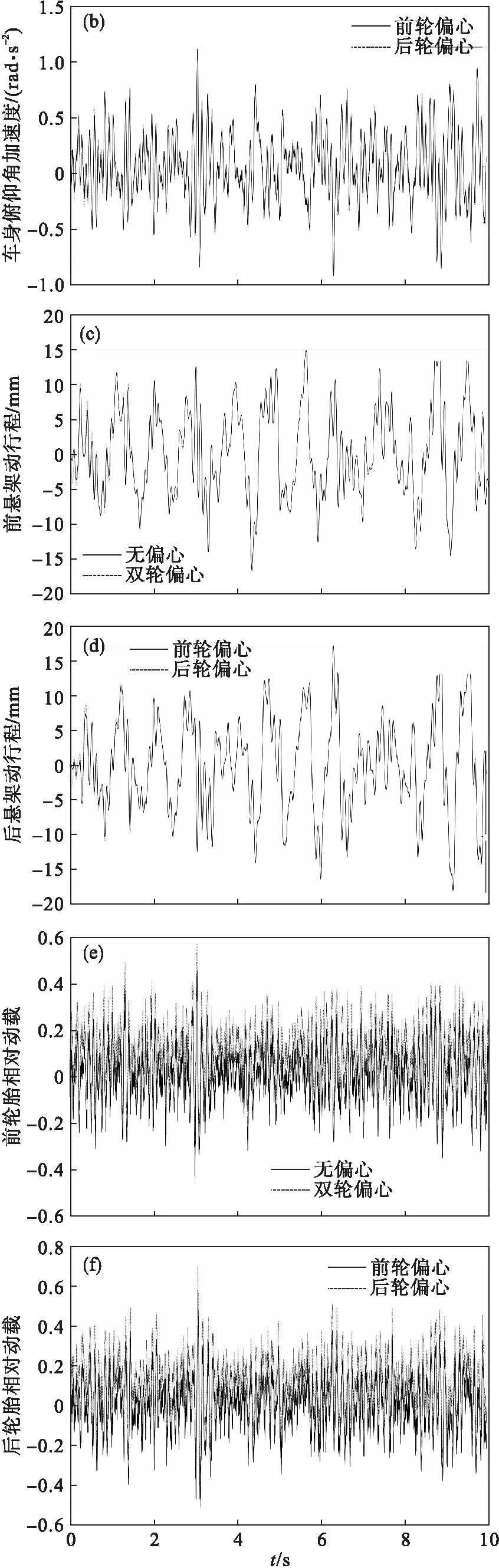
图5 B级路面60 km/h时4种情况的振动响应量
由图5可知,4种情况的各个振动响应量都随着时间变化而变化.
以1 km/h为增量,使车速由1 km/h变化到80 km/h,上述4种情况的评价指标与车速的变化关系,即振动响应量均方根值与车速的变化关系,如图6所示.
由图6可知,在B级路面和不同速度下,轮毂电机电动汽车不同位置的电机偏心对评价指标有着不同的影响.
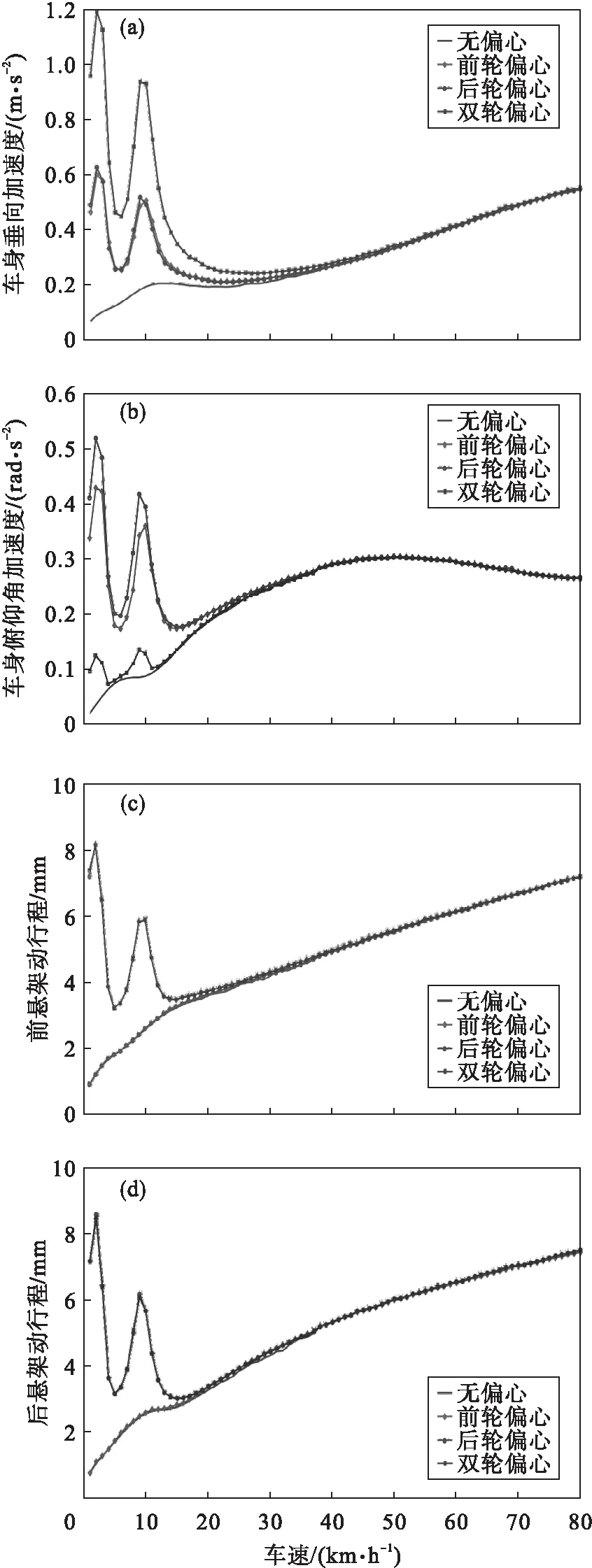
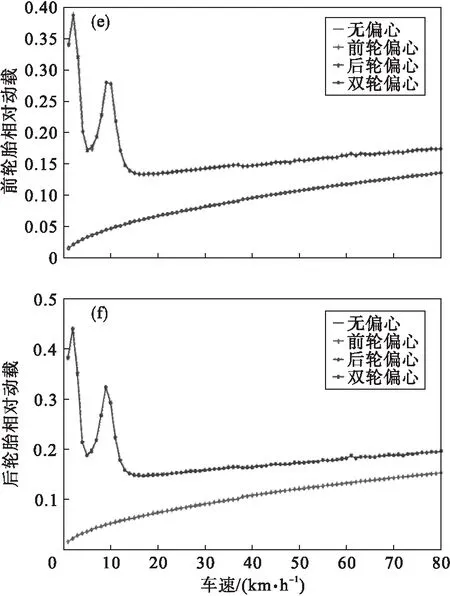
图6 B级路面不同速度时4种情况的评价指标
1) 不同的电机偏心对车身垂向加速度都有影响,在速度4 km/h和10 km/h左右时有峰值;在速度小于35 km/h时,不同的电机偏心都使车身垂向加速度增大,其中双轮同时偏心影响最大;在速度大于35 km/h时,近似于无偏心.
2) 不同的电机偏心对车身俯仰角加速度都有影响,在速度4 km/h和10 km/h左右时有峰值,其中前轮偏心和后轮偏心影响较大;在速度小于20 km/h时,相较于正常悬架增大;在速度大于20 km/h时,近似于无偏心.
3) 前轮偏心和双轮偏心对前悬架动行程有影响,在速度4 km/h和10 km/h左右时有峰值;在速度小于20 km/h时,前轮偏心和双轮偏心时大于无偏心;在速度大于20 km/h时,近似于无偏心;后轮偏心对前悬架动行程影响较小.
4) 后轮偏心和双轮同时偏心对后悬架动行程有影响,在速度4 km/h和10 km/h左右时有峰值;在速度小于20 km/h时,后轮偏心和双轮偏心大于无偏心;在速度大于20 km/h时,近似于无偏心;前轮偏心对后悬架动行程影响较小.
5) 前轮偏心和双轮偏心对前轮胎相对动载有影响,在速度4 km/h和10 km/h左右时有峰值;其他速度范围内大于无偏心;后轮偏心时,对前轮相对动载影响较小.
6) 后轮偏心和双轮偏心对后轮胎相对动载有影响,在速度4 km/h和10 km/h左右时有峰值;其他速度范围内大于无偏心;前轮偏心对后轮胎相对动载影响较小.
4 结 语
建立了轮毂电机电动汽车平面4自由度振动模型,可用于分析电机质量、电机偏心和路面对电动汽车平顺性的影响.采用Matlab/Simulink分别开发了相应的轮毂电机电动汽车平顺性仿真模型,可以实现前轮和后轮的随机路面激励、轮毂电机激励和轮毂电机电动汽车随机路面平顺性仿真.结果表明,电机偏心对轮毂电机电动汽车振动性能有着不可忽视的影响,也体现了轮毂电机电动汽车与传统汽车的平顺性不同.

