考虑舆情的分时段SIQR模型的新冠疫情分析与预测
鲍玉斌, 刘济霆, 李效宇
(1. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169; 2. 东北大学 机器人科学与工程学院, 辽宁 沈阳 110169)
在全球疫情尚未结束的背景下,我国仍然面临着因境外冷链病毒输入或境外感染人员输入等造成的小范围地区性的疫情复发.为有效防止疫情的扩散,各地政府主要采用了调查流行病学排查密切接触者、通过新闻媒体对疫情信息进行快速广播以及大规模核酸检测,确定并隔离感染者的防控措施.许多学者针对疫情的预测展开了大量的研究工作,研究了疫情的传播特点和规律,预测结果也为决策者提供了参考信息.
目前国内外学者用多种手段仿真预测了新冠肺炎的传播过程,但预测模型多是基于 Kermack 等[1]提出的SIR(susceptible infected recovered)仓室模型或SEIR(susceptible exposed infected recovered)仓室模型,并通过增加仓室或改变参数等方式进行优化.其中,周涛等[2]用SEIR模型与Wallinga等[3]创建的基本传染数经验估计公式得出基本病毒再生数R0的取值区间为(2.8,3.3).Yang等[4]应用SEIR模型和LSTM(long-short term memory)模型预测出我国2020年的疫情高峰是在同年的2月下旬,并验证了2020年1月23日武汉封城对抑制疫情发展的重要意义.张琳[5]分阶段拟合了国内疫情早期的确诊人数等数据,并对疫情传播作了预测.Kissler等[6]模拟了不同程度的社交隔离举措对降低疫情峰值和防止医疗系统崩溃的影响.Engbert等[7]在SEIR模型基础上,考虑了新冠肺炎的空间异质性,实现了准确的短期预测.Li等[8]考虑了有力的防控措施的影响,提出一种改进的SEIQR(susceptible exposed infected quarantined recovered)模型.Huang等[9]综合考虑环境因素和不同国家的控制措施,在SIR模型基础上建立新冠肺炎预测系统,并在西方国家的疫情预测上取得良好效果.
现有文献多用武汉疫情数据仿真国内疫情传播情形,未考虑在疫情防控常态化情况下病毒在城市内区域性传播,感染人数增长速度相对平稳等传播特点.此外,如今医疗资源充足,有条件展开大范围核酸检测以排查确诊感染者,并且疫情信息及时准确的披露使人们本能地减少外出,降低与潜在感染者的接触几率,从而一定程度上阻止了疫情的扩散.
为准确预测疫情传播并为管理人员提供有效的防控策略,本文考虑舆情因素与感染者的隔离措施对疫情传播的影响,并综合疫情传播各个时期的特点,建立了一种具有非线性参数的分时段的传染病模型——SIQR(susceptible infected quarantined recovered)模型.它不仅对现阶段准确预测疫情传播有着重要意义,更为政府防疫部门科学有效地防控本土疫情提供决策参考.
1 模型建立与分析
1.1 模型建立
本文在经典的SIR模型基础上,将感染者加以隔离,增加了确诊并被隔离的感染者仓室Q.因为不同的疫情传播时期,存在不同的主要干预措施与强度,故将感染率、隔离率和治愈率等参数分时期地描述,建立了非线性的SIQR模型,以得到更符合现实城市防疫特点的防疫模型.其中仓室S代表易感人群集合,I代表具有感染性但没有被确诊的人群集合,Q代表已被确诊并被隔离的感染者集合,R代表已经治愈的感染者集合.模型仓室之间的状态转移图见图1.

图1 SIQR模型状态转移图
根据SIQR模型仓室的定义及状态转移图,可得SIQR模型的微分方程组如式(1)所示:
(1)
其中,当易感人群S接触感染者人群I后,他们会以一定的感染率β成为感染者.隔离率α描述了防疫部门对感染者检测并隔离干预的强度.被隔离的感染者以一定的治愈率γ成为治愈者.N代表发生疫情的城市人口总数.
1.2 感染率与舆情的关系
新冠肺炎的感染率β可以通过经验的基本病毒再生数R0计算得到.R0的计算公式[10]见式(2):
R0=kbD.
(2)
其中:k是单位时间内感染者的接触人数;b是感染者能成功感染其接触的易感者的概率;D是感染者传播病毒的平均时间.根据R0,k和b的定义,感染率β的计算公式如式(3)所示:
β=kb.
(3)
由于媒体对疫情新闻的报道,减少了人们不必要的外出活动,从而减小感染者的平均接触人数,即媒体对于感染率的影响主要反映在参数k上.
目前考虑媒体影响的模型多采用非线性的递减函数作为感染率函数.如Xiao等[11]用负指数函数表达媒体影响,建立了H1N1流感传染病模型,并发现疫情早期媒体的影响最显著.Pawelek等[12]建立了考虑推特信息影响的流感模型,其媒体影响函数见式(4):
β=β0·e-αT(t).
(4)
函数T(t)描述了易感者、潜伏者和感染者以不同的系数接受信息,并且推特信息以一定速率变得过时的情形.
尽管该流感模型在H1N1流感仿真上表现良好,但不适合描述在疫情防控背景下短时间内的信息传播.此外,文献[11-12]主要从不同仓室受媒体影响的角度,提出了相应的模型.但本土疫情防控的新闻时效性强、受众广泛并且传媒方式丰富,首例病例报告当天同城民众基本都可得知疫情事件的发生.因此可以不考虑式(4)中函数T(t)中不同人群以不同速率接受信息的差别,可对其进行简化.
综合上述考虑舆情影响的传染病模型的特点,本文采用负指数函数作为媒体影响函数.为客观且宏观地描述舆情,采用百度指数量化舆情,它既表示官方媒体对事件的重视程度,又表示民众对疫情事件的关注度.媒体舆情影响函数如式(5)所示:
β=β0·e-nx.
(5)
其中:x代表归一化后的舆情数据变量;n表示媒体对感染率影响的大小,是一个常量系数.
1.3 分时期的模型参数
根据复发的本土疫情实际传播情况,将疫情的传播分为三个时期:第一个时期为疫情传播自由期,零号病人具有感染性但未被确诊,造成了本土疫情传播;第二个时期为疫情传播初期,出现首例确诊病例,但尚未开展大规模核酸检测,并且感染率β受舆情的影响;第三个时期为疫情传播后期,对感染者的排查和隔离是干预疫情传播的最主要措施.
在疫情传播的自由期,防疫部门不知情本土疫情的出现,没有排查并收治感染者,所以设隔离率与治愈率均为0,且感染率不受媒体的影响,是不变的.设这一时期的结束时刻是t1,则该时期的模型参数如式(6)所示:
(6)
在疫情传播初期,防疫部门对于溯源传染病与排查感染者有一定的困难,故此时期隔离率α设为线性增大,以描述增长速度相对平稳的传播初期.感染率β设置为关于舆情变量的负指数函数.设疫情传播初期的结束时刻是t2,则此时期的模型参数如式(7)所示:
(7)
其中,p,q是根据疫情数据计算出来的参数.
由于复发的本土疫情传播周期短,故患者的治愈出院时间应该予以考虑,设为Δt.这段时间内少部分无症状感染者被解除观察隔离状态会使治愈病例人数增加,即首例病例出现后的Δt内治愈率很小,并假设之后治愈率随时间呈指数增长关系,则出现首例确诊病例后的治愈率见式(8):
(8)
其中:t1为疫情传播自由期的结束时刻;h为治愈率增高的快慢;治愈率的取值范围为γ0≤γ≤γmax.
在疫情后期,民众对于疫情的关注度可能仍在升高,即媒体对于感染率仍存在一定的影响.当舆情指数达到峰值后,民众的防疫意识已然形成,故此后感染率不变(x=1).设舆情指数峰值对应的时刻为t3,则疫情后期的感染率见式(9):
(9)
如果疫情后期的隔离率不变,则疫情初期与疫情后期的隔离率大小相等,不符合实际防控过程中防控措施与力度随时间的推移不断增强的特点.因此,在疫情后期,为描述政府干预强度的快速增强,应用非线性递增的隔离率,并使疫情转折点滞后于疫情后期的开始时刻,见式(10):
α(t)=α0·em(t-t2),α0≤α(t)≤αmax.
(10)
其中,参数m描述了隔离干预程度增强的快慢,取值范围通常在(0.15,0.25).
2 隔离率参数求解与讨论
2.1 疫情传播初期的隔离率参数求解
在疫情传播的自由期,没有对感染者排查的干预措施,即没有仓室I到仓室Q的转移过程,此时期是经典的SI(susceptible infected)模型,感染者的微分方程见式(11):
(11)
易感者人数S(t)与城市总人数N的差非常小,可以认为它们的比值约为1,对时间t积分可得感染者人数关于t的函数见式(12):
I(t)=I0·eβ·(t-1),0 (12) 其中:I0是初始感染者人数;t1是疫情传播自由期的结束时刻,则在t1时刻的感染者人数如式(13)所示: I(t1)=I0·eβ·(t1-1). (13) 在疫情传播初期,同样认为易感者人数与总人数的比值约为1,则感染者仓室的微分方程简化成式(14): (14) 设t2是此时期的结束时刻,则式(14)的解为 I(t)=I(t1)·e(β-α)·(t-t1),t1 (15) 模型中仓室Q定义为被确诊的感染者集合,所以官方统计的确诊人数数据包括被确诊的感染者和已被治愈的感染者,即累计确诊人数N(t)的表达式如式(16)所示: N(t)=Q(t)+R(t) . (16) 对式(16)左右两端同时求导,得到疫情初期累计确诊人数的微分方程,如式(17)所示: (17) 将式(15)代入式(17),得到式(18): (18) 对式(18)左右两端同时积分,得疫情传播初期的确诊人数函数N(t),如式(19)所示: (19) 其中,隔离率α是式(7)中定义的关于时间t(t1 通过式(19)对真实确诊人数的数据进行拟合,得到参数p和q,将其代入式(7),即可求得疫情传播初期的隔离率. 对参数m和αmax进行对比实验,根据大连市疫情防控工作公布的传染病流行学调查结果,可以认为疫情传播自由期为5 d,并根据大连市采取排查感染者强度的不同,设疫情传播初期为5 d.大连市疫情自12月15日至次年1月30日共 47 d的确诊人数数据在辽宁省卫健委官方网站可得(1)http://wjw.shenyang.gov.cn/.从百度指数官网(2)https://index.baidu.com/得到大连市疫情初期的舆情数据. 设归一化后舆情数据变量x=0时有平均接触人数k1=10[13],当x=1时有平均接触人数k2=8.根据式(3)和式(5)易求得参数n: (20) 根据文献[2],设R0为3.3,并设置感染者传播病毒的平均时间t=7 d,根据式(2),式(3)可以求得β0.综上,对比实验参数设置如表1所示. 表1 除m和αmax外的模型参数Table 1 The model parameters except m and αmax 为讨论疫情传播后期隔离率α(t)计算(见式(10))中参数m和αmax的效用,设参数αmax为0.6,仿真不同参数m时累计确诊人数随时间的变化情况,如图2a所示.同理,设参数m为0.2,仿真不同参数αmax时累计确诊人数随时间的变化情况,见图2b. 图2 参数m与αmax分别为控制变量的对比实验 由图2可以看出,参数m的变化使得增长曲线的变化较大.相比之下,参数αmax的变化却没有使增长曲线表现出较大的变化.从最后的确诊总人数看,m值的变化使其有明显的差异,而αmax的不同使曲线的平缓趋势有所不同.因此参数m主要决定曲线的增长趋势,而参数αmax主要决定着曲线最终的平稳趋势. 疫情转折点是衡量疫情控制效果的关键,需要定量地计算.本模型中感染者人数I的微分方程为 (21) 疫情的转折点为感染者人数开始减少的时刻,即式(21)小于0的时刻,故此时的隔离率为 (22) 为定量地说明参数m和αmax对疫情防控的干预程度,根据式(22),计算得到图2a对应实验中参数m不同取值条件下的疫情转折点,如表2所示.当m=0.2时,αmax不同取值的疫情转折点如表3所示. 表2 参数m取值对疫情转折点的影响Table 2 The impact of m value on the turning point of the epidemic situation 表3 参数αmax取值对疫情转折点的影响Table 3 The impact of αmax value on the turning point of the epidemic situation 表3中αmax取值不同时的疫情转折点相同,说明一定范围内变化的αmax对于疫情干预影响较弱,仅使确诊总人数有一定的差异.但是表2显示参数m的变化将疫情转折点时间提前,使得疫情提前控制,最终感染总人数也会减少.因此,防疫部门对疫情的反应速度一定程度上决定了最终的感染人总数. 3.1.1 SIQR模型预测累计确诊人数 从预测与决策的角度看,舆情指数的峰值选择为首例确诊病例确诊后8 d内的高峰值,而时段的划分是需要决策者根据疫情发生的实际情况作出判断,如发生地是否为人员密集流动区,传染链是否已存在较长时间等.根据不同的疫情转折时间点,用疫情传播初期的数据可以预测最终累计确诊人数的范围. 实验数据为2.2节提及的大连市疫情数据与舆情数据.根据传染病流行学调查结果及大连市疫情防控工作报告,设疫情传播自由期和传播初期均为5 d.基本再生数R0沿用2.2节中的取值,分时期的感染率、隔离率用式(6),(7),(9),(10)计算.累计确诊人数是隔离者和治愈者数量之和,故不需考虑治愈率参数. 疫情传播初期的隔离率公式(见式(7))中的参数p和q由式(19)对12月15号至12月17日的确诊人数进行有约束的拟合得到,拟合工具为Python及Imfit包.由2.2节的讨论可知,αmax不影响转折时间点,因此主要讨论不同疫情转折点下的参数m取值范围和最终感染人数等,本模型的部分实验参数值见表4. 表4 模型主要参数Table 4 Model parameters of simulation experiment 为描述疫情得到控制后的稳定状态,定义疫情平稳时间为连续3 d确诊人数的增长值小于1,即 N(ti)-N(ti-1)<1 . (23) 根据实际情况设置疫情转折点为出现首例确诊病例后的第8天至第10天.据此计算m的取值范围、总感染人数以及平稳期,结果见表5. 表5 不同转折点条件下的预测结果Table 5 The predication results at different turning points 由表5可知,参数m的取值随着疫情转折点的推移而减小,并且最终的感染人数与平稳期的数值均有明显的分段.如果m取值为区间的中间值0.20,当疫情在第9天达到转折点,且最终确诊人数预计约为85时,预测曲线如图3所示. 3.1.2 不同预测模型对比 为了说明本模型更适用于预测“后疫情”时代本土疫情变化趋势,将其与Logistic模型,Logistic与SEIR结合模型(Logistic-SEIR)[14]相对比.文献[14]对Logistic-SEIR模型的参数进行了讨论,SEIR模型参数S0=1.35K0,E0用Logistic模型中的参数P0初始化,I0设为第1天的感染人数,传染率初值设为0.25. 图3 大连市疫情累计确诊人数的预测结果 因为Logistic模型只能预测累计确诊人数,而且本文模型的治愈率参数较难从预测角度确定,故上述三种模型的预测对象为累计的确诊人数.上述两种对比模型的数据集依据已知确诊人数的天数来划分,分别为10,13,16 d,预测结果见表6.本模型的已知天数为8d,评价指标采用均方根误差RMSE,即 (24) 其中:pi和ti分别是第i个时刻的仿真值和真实值;τ表示疫情传播全时期的天数. 表6 不同模型的预测性能Table 6 The predictive performance of the different models 由表6可知,本模型与Logistic模型的预测范围接近,而Logistic-SEIR的预测范围比实际值偏高.本模型需要的已知天数较少,但需要决策者对疫情转折点作出判断,而Logistic模型在已知天数较少时(如8 d),预测的最终确诊人数值会远超实际值.Logistic-SEIR模型也是如此. 本模型(m=0.20)、Logistic模型和Logistic-SEIR模型(已知天数都为13 d)的累计确诊人数见图4. 图4 不同模型的预测性能 本模型与Logistic模型预测的疫情变化趋势与实际一致,而Logistic-SEIR模型的预测结果与实际不符. 综上,本模型可以较好地预测复发的本土疫情累计确诊人数与疫情发展的变化趋势. 为了说明考虑舆情的SIQR模型的效果,将其与感染率β0不变的SIQR模型分别拟合大连市2020年12月真实的疫情确诊人数曲线,进行对比实验.因为本文实验t=0是首例病例的确诊时间,考虑患者治愈出院时间对模型的影响,设首例病例出现后15 d内,治愈病例数量很少,故此时间段内的治愈率很小.文献[14]对治愈率研究的结论是不断增大治愈率会使模型表现更好,则公式(8)的参数取值为γ0=0.01,h=1/5和γmax=0.5,m=0.21,其余参数设置见表4. 对比实验仅感染率定义不同,其余参数均相同,得到疫情变化的仿真曲线如图5a和图5b所示.非线性感染率模型的仓室Q与R的仿真曲线如图5c和图5d所示,Q(t)与R(t)的值分别为现有确诊人数和累计治愈病例数. 从图5a中可以看出考虑舆情的SIQR模型仿真结果与真实的确诊人数变化趋势相符,而图5b中未考虑舆情的曲线趋势远超过了实际的变化过程,误差较大.尽管增大隔离率参数可以使得最终确诊人数与实际相近,但确诊人数的增长速度将非常快,与实际不符.图5c和图5d中的Q(t)和R(t)仿真曲线均与真实的变化趋势一致,其与真实值的均方根误差分别为3.48和3.63,进一步说明了本模型的仿真结果较好.应用本模型在考虑舆情与未考虑两种情形下进行仿真,结果见表7. 图5 大连市疫情仿真结果 表7 考虑舆情与未考虑舆情的模型仿真结果Table 7 Simulation results of models considering and not considering public opinion 表7中考虑舆情的仿真误差仅为2.13,说明仿真结果与真实值相近.疫情转折点在疫情后期第9天到来,从确诊人数的数据上看,也比较符合真实的情况.而未考虑舆情的仿真误差值较大. 因此,本文所提出的考虑舆情的SIQR模型不仅预测准确度较高,而且能够更好地拟合疫情发展的变化趋势,改进效果明显. 通常情况下,复发的本土疫情具有确诊人数增长较为平稳的特点.但也不乏例外,如2020年6月北京新发地疫情以及2021年初河北省疫情.这类疫情往往具有传播自由期较长,发生过聚集性感染以及疫情防控响应速度快等特点.因此,为说明本文模型的健壮性与实用性,现对北京新发地疫情进行全时期的仿真模拟. 从北京市卫健委官网(3)http://wjw.beijing.gov.cn,收集了北京市2020年6月11日至8月6日共57 d的确诊病例和治愈病例数据.在百度指数官网收集了关于“北京疫情”关键字的舆情数据,相比于大连12月疫情时的舆情数据,北京的舆情指数远高于大连的,说明北京疫情扩散受媒体影响更大.所以设x=0时的平均接触人数k1=10,当x=1时平均接触人数k2=7.根据式(20)可以求得参数n. 根据北京市卫健委公布的流行病学调查结果,认为5月31日为疫情传播自由期的开始时间,共11 d.由于防控部门响应迅速,并且日均检测量高,故疫情初期为2 d.初期第1天出现确诊病例,只需对第2天的隔离率α0作出设置(α0是疫情初期最后一天隔离率的值),故无需再拟合求隔离率.根据实际防疫强度,α0可以在区间[0.1, 0.2]之间取值,使疫情确诊人数的增长曲线较为贴合实际.由于北京新发地属于人员聚集区,故设R0为3.5,病毒传播的平均时间D不变.参考3.2节治愈率参数的设置,取Δt=20,γ0=0.01,h=1/7和γmax=0.5.其余参数见表8. 根据表8中的模型参数,用本文模型对北京市2020年6月疫情进行全时期仿真,得到累计确诊人数的拟合曲线与潜在感染者人数的估计曲线见图6a,仿真中仓室Q与R的变化曲线见图6c和图6d.为与本文模型的拟合效果作对比,用Logistic模型同样进行全时期的仿真模拟,结果如图6b所示. 表8 仿真实验的模型参数Table 8 Model parameters of simulation experiment 图6 北京市疫情仿真结果 用式(22)计算得到本模型疫情仿真结果的转折点,则本模型与Logistic模型对北京市疫情进行仿真,结果见表9. 表9 北京市疫情仿真结果Table 9 Simulation results of Beijing epidemic 从图6a可以看出该模型得到预测曲线的变化趋势与实际确诊人数的变化趋势一致,预测值与真实值相近.根据仿真结果,在首例病例确诊后第5天即为疫情的转折点,可知北京市对这次疫情的防控强度大,反应速度快,但是由于病毒已传播一段时间,并且源头为人员密集地区,所以造成了较多人员的感染.模型仿真值与真实值的均方根误差为8.00,且比Logistic模型的误差小,并且平稳时刻的估计值更符合实际.相较于确诊人数的量级,预测值与真实值误差不大.但本文模型的Q(t)和R(t)曲线与真实的误差分别为18.59和18.04,误差较大的原因在于现有确诊人数的峰值高且处于峰值时有段时间数值变化很小. 综上,本模型对于疫情传播自由期长,存在聚集性感染情况的本土复发疫情也有较好的拟合效果,因此,模型的适应性与健壮性较好. 本文针对本土疫情防控的特点,将舆情因素纳入模型,提出了分时段的COVID-19疫情预测SIQR模型,并在实际数据上进行了对比测试,验证了本文模型具有较好的预测性能和鲁棒性.本文的模型可以通过选择不同的疫情转折点, 对 全时期疫情变化趋势以及确诊总人数作出相应的预测,可为决策者提供参考.根据实验结果分析发现,如果由转折点计算得到的m值在(0.15,0.25)之间,那么预测的结果较好.全时期疫情数据的拟合结果表明,用舆情数据修正得到的感染率能较好地适应各时期疫情扩散的特点,使全时期疫情传播的仿真结果更佳.
2.2 疫情后期隔离率参数讨论




3 实验与结果分析
3.1 预测模型评估与对比


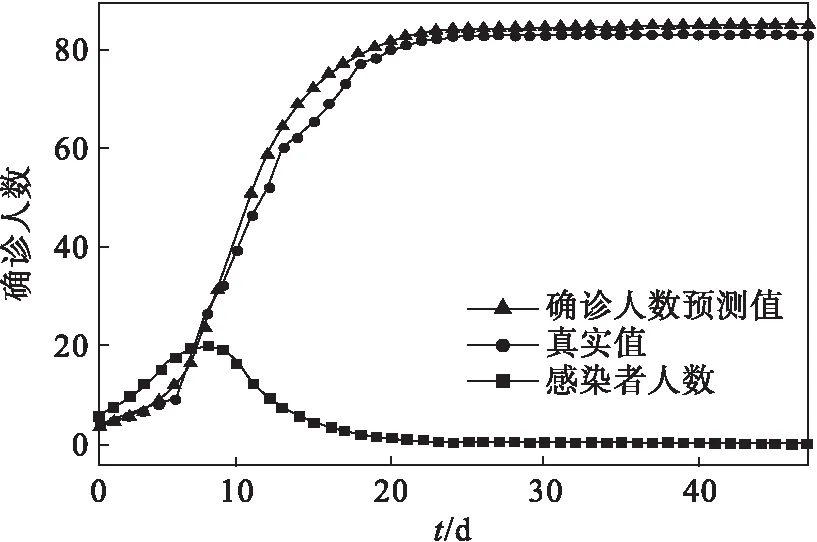


3.2 考虑舆情对SIQR模型的改进效果


3.3 对传播自由期较长的疫情的仿真模拟



4 结 语

