基于谐响应分析的振动试验仿真计算方法研究

别 瑜，肖烨然，肖 霆

应用研究

基于谐响应分析的振动试验仿真计算方法研究

别 瑜，肖烨然，肖 霆

（船舶综合电力技术重点实验室，武汉 430064）

本文介绍谐响应分析的基本理论，结合谐响应理论解释扫频试验和定频试验的原理。以中国船级社的振动试验参数为试验条件，研究试验参数条件统一化处理方法、扫频试验和定频试验的仿真分析方法。最后，以LC滤波器为对象，进行了仿真分析及优化设计。

扫频试验定频试验谐响应仿真分析

0 引言

产品在运输或者使用过程中，会受到环境中各种振动的影响，为了保证产品的质量和可靠性，通常会进行振动试验[1～2]。常用的振动试验，根据激励的不同可分为随机振动试验和正弦振动试验，其中正弦试验比随机试验的应用更为广泛。正弦试验又分为扫频试验和定频试验，目的是检查产品的共振频率，并对共振频率进行耐振测试，以提高产品通过耐振处理后的可靠性。对于船用设备，需要通过船级社的认证，更是要通过振动试验。中国船级社在《电气电子产品型式认可试验指南》中，对振动试验的试验条件和振动参数进行了规定。目前产品振动分析主要以试验研究为主[3,4]，做振动试验需要一定的时间成本和物料成本。在产品的设计阶段，采用仿真分析的方法替代振动试验对产品性能有效评估，对提高产品设计质量、缩短产品研发周期具有重要意义。

1 谐响应分析的理论基础

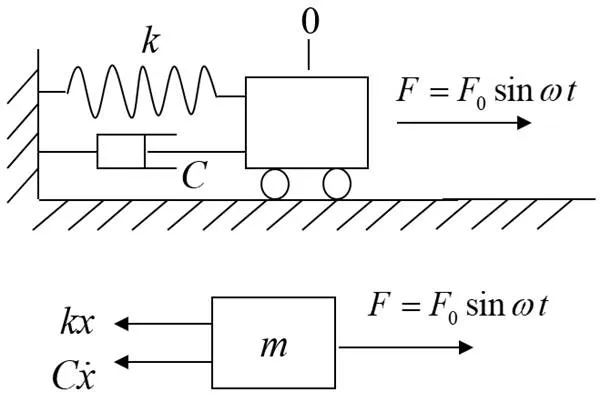
图1 单自由度系统振动模型

正弦振动试验的本质就是谐响应，即当扫频的频率与产品的固有频率接近时产品在激励作用下的振动幅值会放大，一定条件下甚至会发生共振，谐响应分析就是研究结构在不同持续频率的周期载荷作用下产品的响应特性，包括加速度响应、应力、位移等，其所受的载荷为简谐载荷[5～6]。图1所示为单自由度系统的振动模型在简谐力的作用下的示意图，物体与水平地面的摩擦以及空气阻力忽略不计。

根据牛顿第二定律，可得振动系统的微分方程

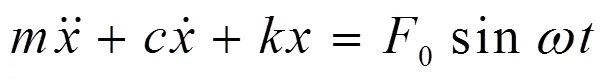
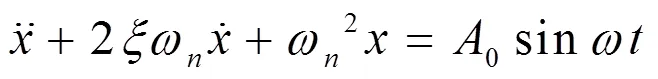
由于实际的机械振动多为欠阻尼(0<ξ<1)振动，这里不讨论临界阻尼(ξ=1)、过阻尼(ξ>1)和无阻尼(ξ=0)的情况，仅讨论欠阻尼的情况。

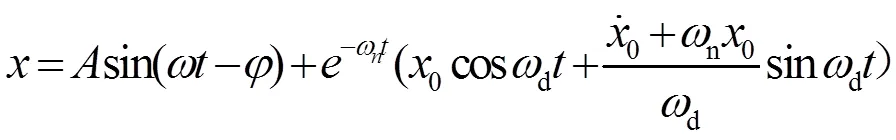
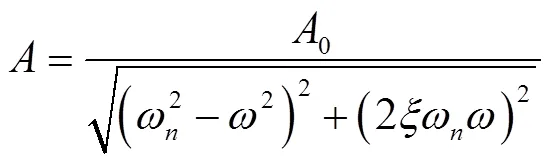
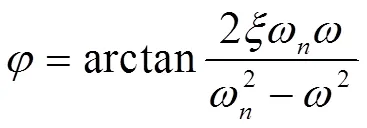
将方程的解（3）分成两部分，即

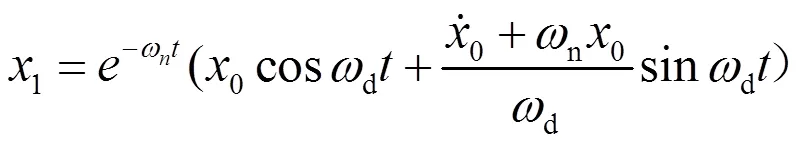
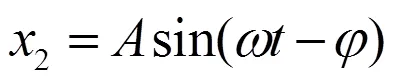
分别绘制x、x1和x2的曲线，如图2所示

2 振动试验的仿真分析计算方法

由于扫频试验和定频试验的本质是谐响应，因此可以通过谐响应分析来模拟扫频试验的定频试验来对产品的振动特性进行评估。

2.1 扫频振动仿真分析

扫频试验，就是在一定范围内连续改变周期性外力的频率，检验试验对象在不同频率的简谐力作用下的响应，是否存在共振频率。定频试验，主要是对共振的频率进行耐共振试验，确保产品在工作频率范围内不出现共振破坏或振动疲劳。

由振动微分方程的解（3）和对应的响应曲线可知，在简谐力作用下的响应的稳态解是受迫振动，即受迫振动占主导地位，即

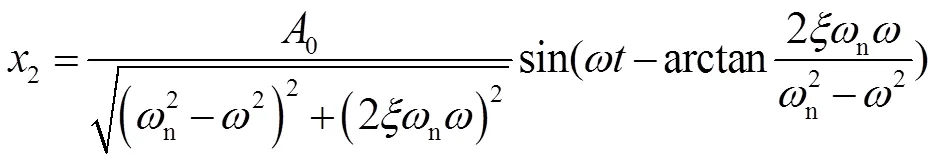
扫频试验就是连续改变的值，通过响应的幅值A来找出共振频率。若阻尼比ξ=0，当趋近于ω时，A的值趋近于无穷大；实际上ξ≠0，当=ω时，响应幅值A为一个有界数值，阻尼比越大, 则A越小。通过仿真分析，对发生共振的结构进行改进优化，通过增大结构阻尼、提高结构强度，降低A的值，确保结构可靠不被损坏。

以中国船级社的《电气电子产品型式认可试验指南》中振动试验参数为例，对振动试验的仿真分析方法进行研究，如表1所示。

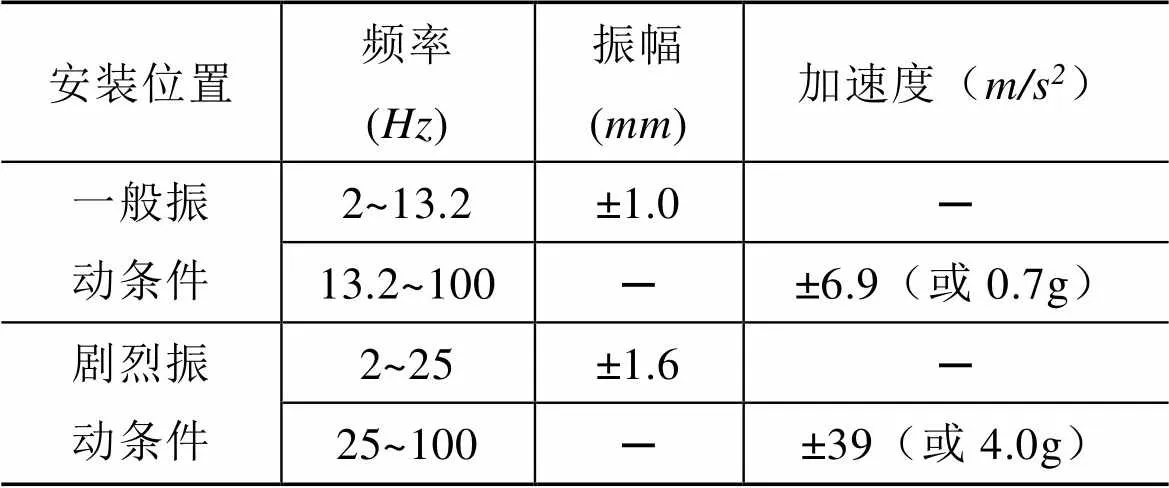
表1 振动试验参数

其中，试验方法要求，扫频范围可限制在临界频率的0.8～1.2倍之间，扫描无明显共振点，则在30 Hz下作90 min耐振试验，如有共振频率，则在振幅放大率≥2的共振频率上作90 min耐振试验，试验应在3个互相垂直的轴线上进行。

由振动试验参数可知，低频段定振幅振动，高频段定加速度振动，振动参数不同无法进行直接仿真计算，需要统一起来。对于谐响应分析，可以将位移参数转换为加速度参数，将振动参数统一起来，转换公式可以按以下公式（8）计算。

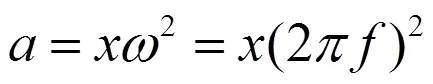
其中a为转换后的加速度，f为扫频频率，x为试验标准规定的位移参数。

以一般振动条件为例，统一加速度参数后的参数曲线如图3所示，仿真计算时，加速度振动参数需要以表格的形式输入。

2.2 定频振动仿真分析计算

对于定频振动，则是在谐响应分析中，将扫频的频率范围设置为单个共振点的频率；若是有两个及以上的共振频率相隔比较近，则可以将这几个共振频率以区间扫频的方式来替代离散的多个点的定频振动。

定频振动试验的目的，主要是测试被试对象在共振点的强度及疲劳强度，因为在共振点处被试对象结构的形变和应力都相对较大，是结构失效最先发生的部位[7-9]。定频振动疲劳多为高周疲劳，其所受的交变应力远低于材料的屈服极限，通常用疲劳曲线（S-N曲线）来描述该材料的疲劳特性，按公式（9）计算。

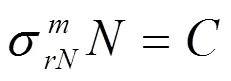
当>0时，循环应较力小，循环次数较大，为无限寿命区；当≤0，循环应力大，为有限寿命区，需计算循环次数。

扫频实验的仿真分析，得到结构的共振频率，根据定频振动大纲要求，在共振频率处进行定频振动90 min，则可计算振动循环次数

=90×60×（10）

通过定频振动仿真分析，可以计算结构在定频振动下的应力值，最后按疲劳计算公式，通过振动循环次数和应力值来校核疲劳强度。

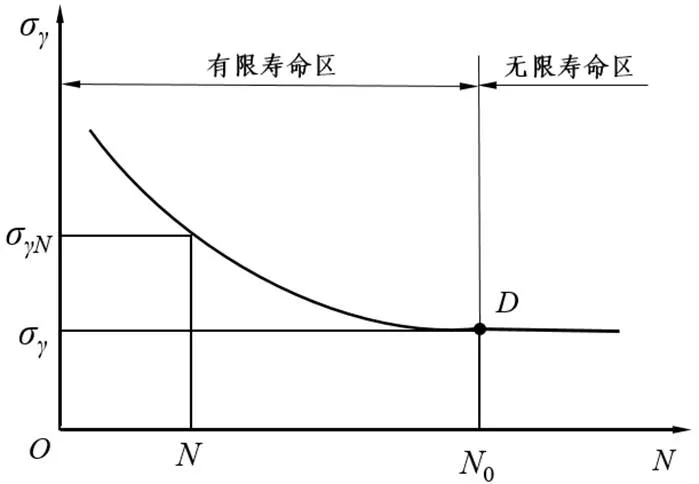
图4 材料疲劳曲线

3 模态叠加法的谐响应分析

谐响应分析可以通过完全法和模态叠加法两种方式实现[10]。完全法谐响应分析的特点：①求解准确；②求解速度慢于模态叠加法；③支持所有类型的载荷和边界条件；④求解频率必须分布在激励频率范围内；⑤使用稀疏矩阵求解。模态叠加法谐响应分析的特点：①提取模态阶数越多，求解结果越精准；②求解速度快于完全法；③不支持非零的强迫位移载荷；④频率点可等间隔和不等间隔分布；⑤使用具有正交关系的模态振型向量的线性组合对控制方法进行解耦。

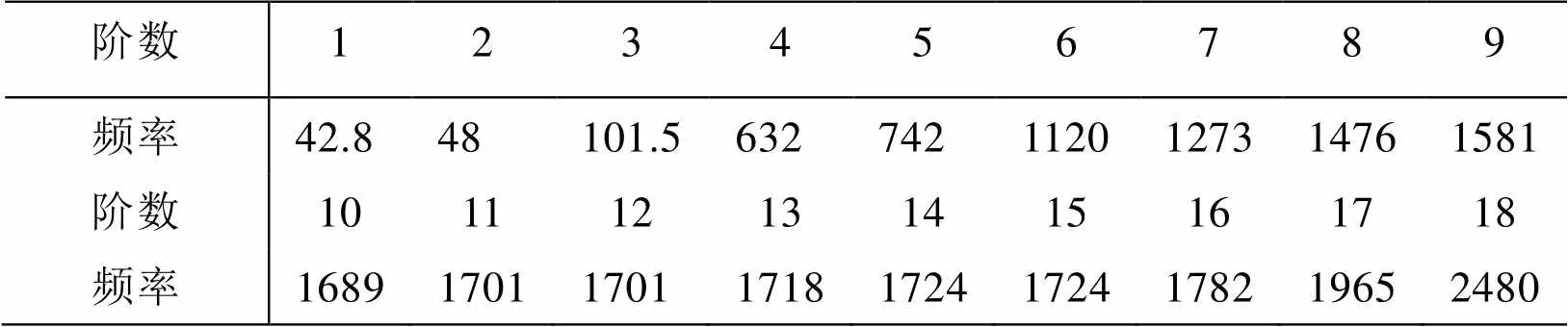
表2 模态分析固有频率

表3 模态分析质量参与因子

考虑到求解时间，以及求解频率分布的特点，选择模态叠加法的谐响应分析。本文以LC滤波器为例，对振动试验仿真分析方法进行研究。

3.1 模态分析

模态分析是动力学分析的基础，谐响应分析前需要先进行模态分析，模态分析要求参与质量达到85%以上才能得到合理的求解结果。

由模态分析结果可知，前三阶固有频率在测试频率110 Hz范围内，应重点分析，前三阶固有频率对应的振型如图5所示。

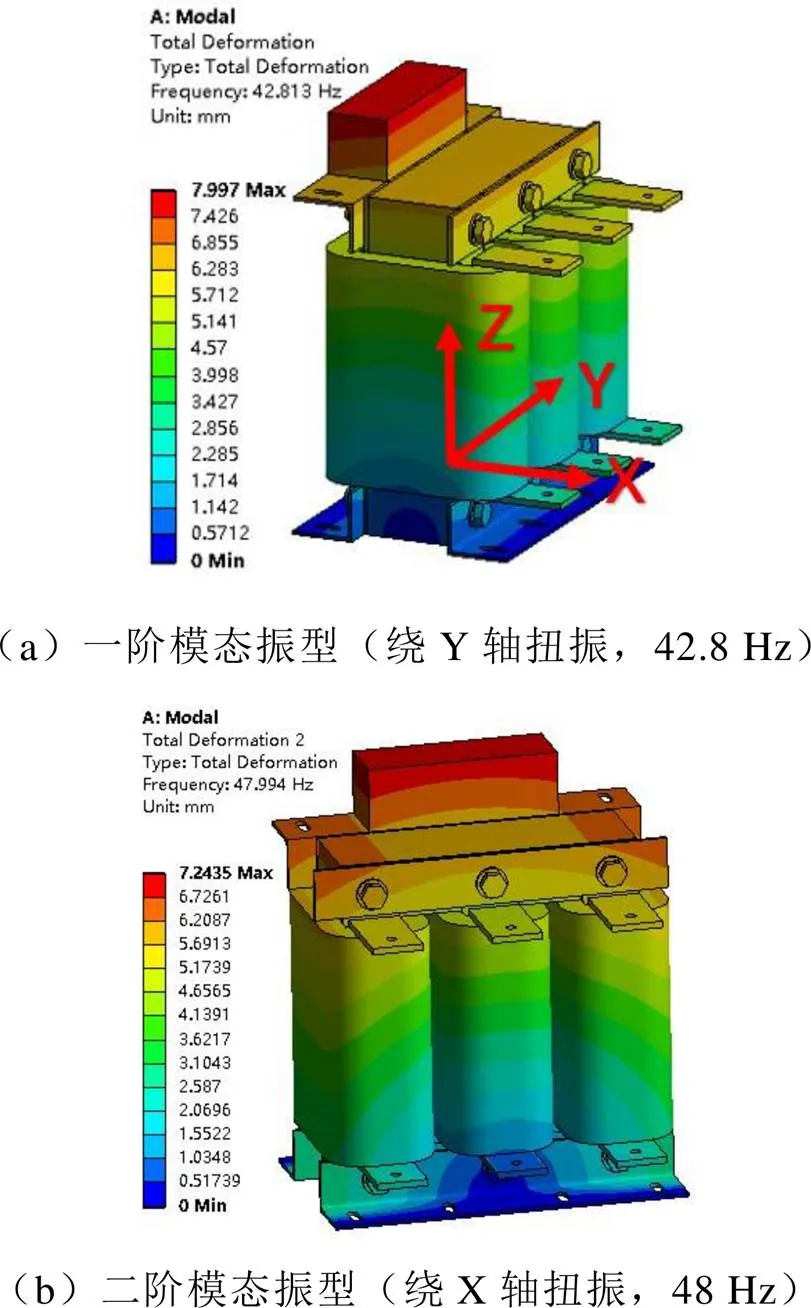
3.2 谐响应分析

3.2.1 扫频振动仿真分析

为了包含振动参数的频率范围，将扫频的最大频率提高到110 Hz，并分别对LC滤波器的X、Y、Z三个方向进行扫频，选取LC滤波器硅钢片上平面为响应输出，得到三个方向的加速度响应曲线，如图6所示。

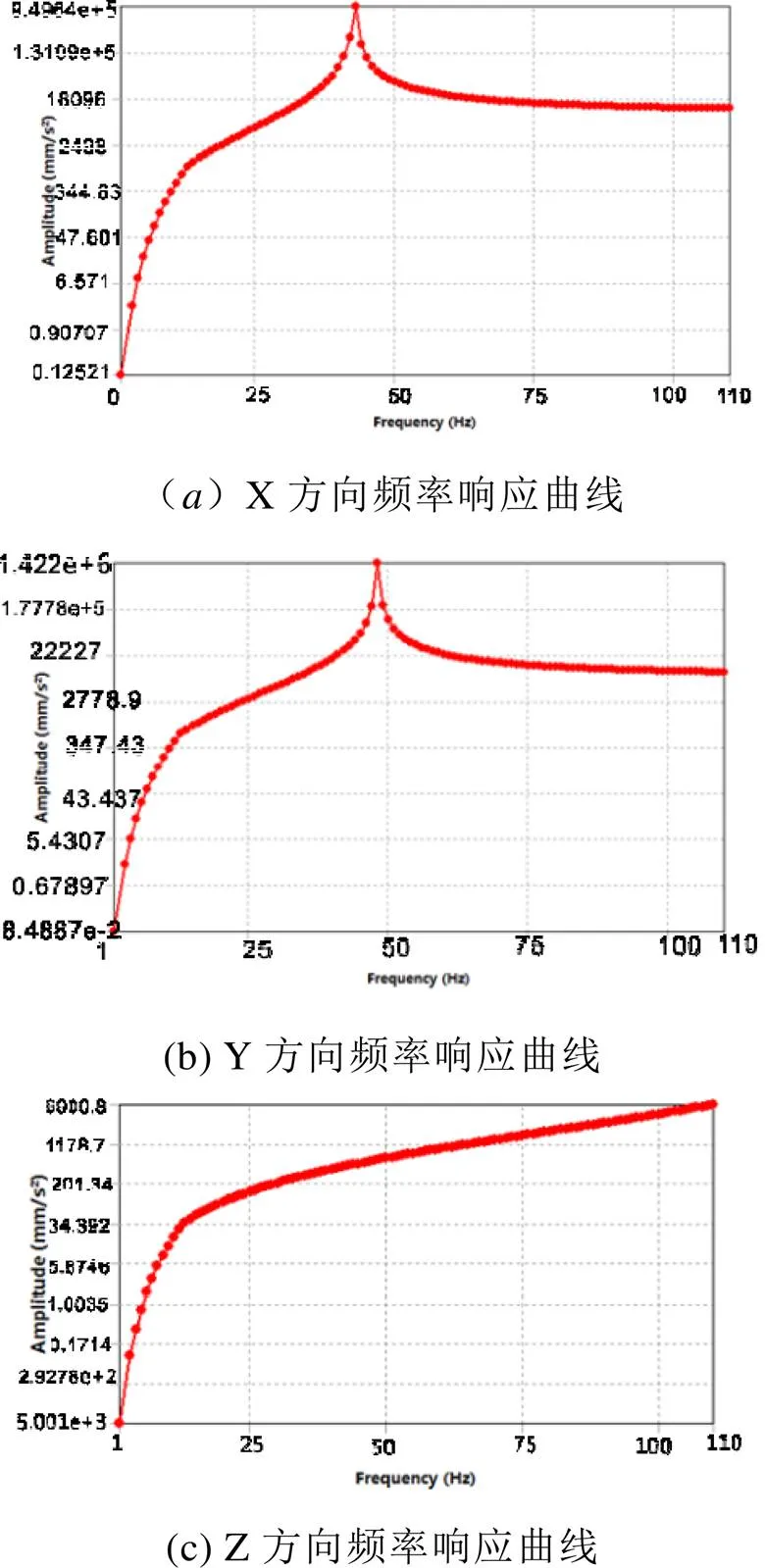
图6 扫频振动仿真响应曲线

由扫频响应曲线可知，在X方向和Y方向出现了共振点，Z方向无共振点，其中X方向共振点的振动频率为43 Hz，与模态分析结果的二阶模态对应，Y方向共振点的振动频率为48 Hz，与模态分析结果的一阶模态对应，三阶模态对应的Z方向未发生共振。根据扫频分析结果，需要对共振频率点进行定频振动分析。

3.2.2 定频振动仿真分析

定频振动分析主要是通过仿真分析计算结构的最大应力是否在材料的强度范围内，以及在该应力下的应力循环次数是否会发生疲劳损伤或疲劳失效。图7所示为X、Y、Z三个方向定频振动分析的应力云图，由应力云图可知， X方向定频振动应力对大，最大应力分布在LC滤波器支架底座的直角边根部，最大应力值为47.24 MPa，需进行疲劳校核。

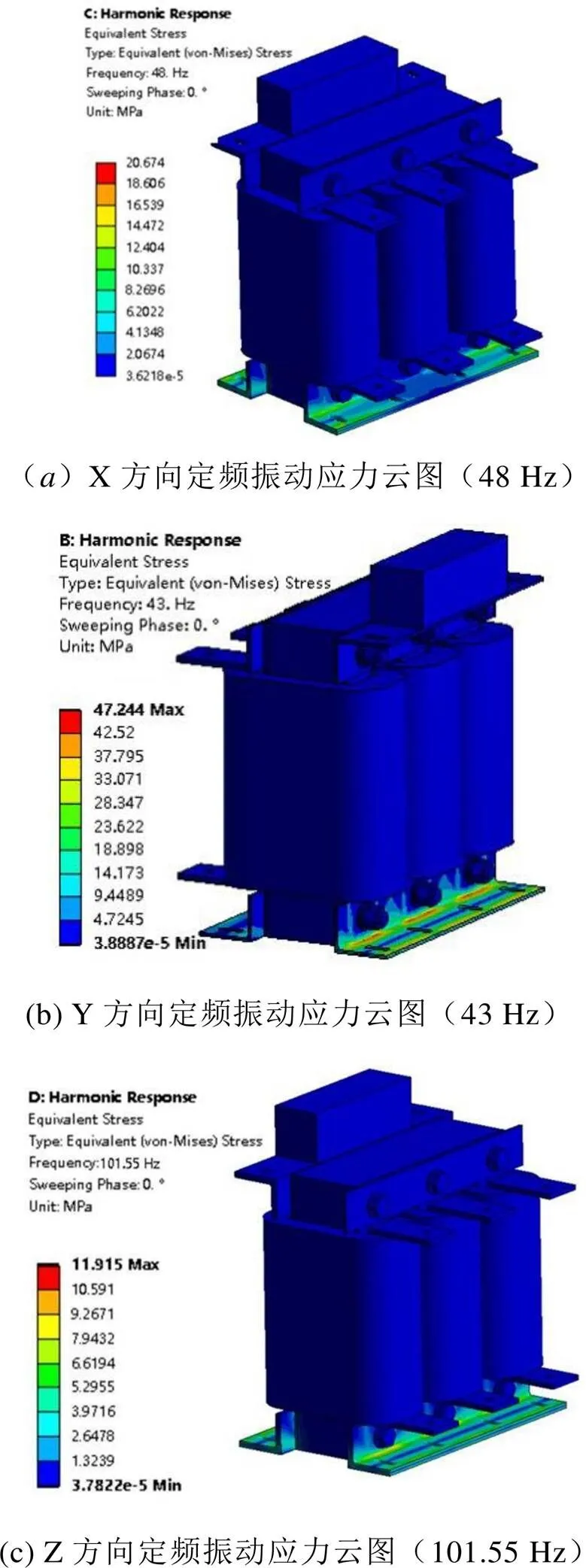
图7 定频振动分析应力云图

定频振动的简谐力为X方向循环加载，与一阶模态振型对应，即绕Y轴振动，引起沿X或绕Y轴转动方向的位移最大，该定频振动使得对应LC滤波器支架底座的应力状态为对称循环应力。

LC滤波器支架底座材料为Q235，底座支架为轧制钢板且无焊缝，根据钢结构设计规范 GB 50017-2017，其材料参数为N=2×106，=4，=1940×1012，可计算N对应的循环应力σ。

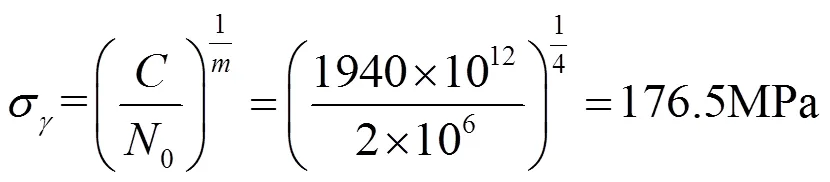
取安全系数K=1.5，则需用应力为

即当循环应力不大于118 MPa时，循环次数≥0，LC滤波器处在无限寿命期。

事实上，将=43 Hz带入公式（9），可得试验振动次数=2.32×105，再将σ=47.24 Mpa带入公式（9），计算振动循环次数

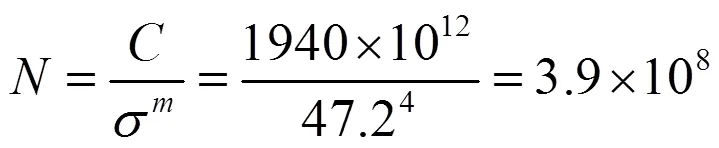
试验振动次数远小于振动疲劳寿命N，LC滤波器不会发生振动疲劳破坏。

4 小结

本文研究了扫频振动试验和定频振动试验的仿真分析方法，重点针对扫频振动试验和定频振动试验的参数处理和计算方法进行了阐述，以LC滤波器为例进行了的振动仿真分析和优化，满足振动试验要求。同时，根据本文研究内容得到一些结论：

1）支撑底座的刚度将直接影响低阶固有频率的大小，提高支撑底座的结构刚度，可以提高低阶固有频率，避免在测试频率范围内出现共振点；

2）在滤波器顶部增加约束，可以提高低阶固有频率，避免低频段出现扭振；

3）对于质量相对集中的结构，其支撑结构宜布置成关于质心对称，避免产生振动耦合。

[1] 刘虎, 周纪磊, 张荣芳, 史嵩, 位国健. 垂直振动激励下排种器振动试验台可靠性分析和验证[J]. 农机化研究, 2021, 43(08): 158-163.

[2] 叶日贵. 多层钢结构振动台试验与数值模拟分析[J].钢结构, 2019, 34(02): 77-80.

[3] 于晨阳. 基于模态加速度法的振动谐响应修正研究与并行实现[D]. 中国工程物理研究院, 2019.

[4] 汪小银, 单颖春, 刘献栋, 何田, 吴金涛. 正弦扫频及随机激励颗粒阻尼器减振效果比较[J]. 噪声与振动控制, 2014, 34(05): 198-202+209.

[5] 郑彬, 鄂靖元. 发动机连杆有限元模态分析及谐响应分析[J]. 机械设计, 2020, 37(S1): 98-101.

[6] 郑彬, 钟发, 张敬东, 蒋勇, 范兴平. 鼓式制动器模态及谐响应分析[J].中国农机化学报, 2020, 41(04): 117-122.

[7] 薛立鹏, 李文斌, 司群英, 叶超, 孙善秀. 运载火箭结构振动疲劳损伤的工程分析方法[J]. 导弹与航天运载技术, 2019(02): 35-38+48.

[8] 王群, 李志远. 基于正弦扫频振动试验的某型车辆点火线圈支架疲劳分析[J]. 四川兵工学报, 2012, 33(07): 78-79+99.

[9] 张莉. 某型电子设备机箱振动疲劳分析[J]. 电子机械工程, 2009, 25(01): 1-5.

[10] 由于, 张伟, 高翔, 黄文超.基于模态叠加法的航空发动机轮盘振动特性研究[J].应用力学学报, 2020, 37(02): 661-665+934.

Research on simulation calculation method of vibration test based on harmonic response analysis

Bie Yu，Xiao Yeran，Xiao Ting

（National Key Laboratory of Science and Technology on Vessel Integrated Power System, Wuhan 430064, China）

introduces

TM761

A

1003-4862（2022）07-0055-05

2021-08-26

别瑜（1987-），男，硕士，研究方向：电气结构设计与仿真分析。E-mail:bieyu712@qq.com