基于Cut-and-Choose技术的安全多方计算
赵 川 徐 俊
1(济南大学信息科学与工程学院 济南 250022)2(山东省网络环境智能计算技术重点实验室(济南大学) 济南 250022)3(山东省软件工程重点实验室(山东大学) 济南 250101)
随着物联网以及互联网信息技术的不断发展,数据正呈现急速增长的趋势,动辄达到数百TB甚至数十至数百PB,标志着大数据时代的来临.同时,这一趋势也推动了机器学习和人工智能研究的浪潮.人脸识别、疫情监测、智慧医疗等应用逐渐改变人类的生产、生活方式.然而,在这些应用背后,个人隐私数据被各类企业收集事件屡见不鲜,引起国内外的广泛关注.如何在确保用户隐私和数据安全的情况下完成某项计算任务,是一项亟待解决的重要问题.
在密码学研究中,安全多方计算(secure multi-party computation, MPC)是一种非常重要的密码学原语,由Yao[1]在1982年首次提出.MPC能够使各参与方联合计算任意的功能函数(functionality),而不暴露他们各自的私有输入和输出.具体地说,在MPC场景中,n个参与方Pi(i=1,2,…,n)希望对他们的私有数据xi联合计算一个目标函数F(x1,x2,…,xn)=(y1,y2,…,yn).在计算完成后,所有的参与方Pi应获得自己的相应输出yi,而不能获取到其他任何信息.一个安全的MPC协议,能够保证多个互不信任的参与方即使在面对某些参与方不诚实的行为时,也能确保诚实方输出的正确性以及输入的隐私性.目前,MPC已经被应用于统计数据分析[2]、邮件过滤[3]、云计算服务[4]和隐私保护机器学习[5]等领域.
1986年,Yao[6]提出了一个安全两方计算协议,将要计算的目标任务表示成布尔电路,并进一步构造出混淆电路,允许双方能够基于各自的输入对电路进行计算,同时不会向对方泄露任何私有信息.然而,该协议只能抵抗半诚实敌手的攻击,不能保证协议运行结果的正确性,也不能保证公平性(即一方可能在另一方获得输出之前掌握了自己的输出,并提前终止协议).恶意敌手可以采取任何策略破坏协议从而获得其期望的结果.为了抵抗这种攻击,一种经典的方法是采用零知识证明[7-8]来验证协议中每一步执行的正确性,从而确保参与方严格按照协议规定执行.但是这种情况下,协议的效率十分低效.尽管文献[9-10]提出了较为高效的解决办法,然而并不适用于大规模的计算任务.
一种更高效的方法是采用Cut-and-Choose技术来检查混淆电路[11-14].在构造电路时,电路构造方Alice并不是生成1个混淆电路发送给计算方Bob,而是构造s个混淆电路并发送给Bob.然后Bob对这些电路进行划分,随机选择打开一部分电路作为检查电路,并利用Alice发送的随机种子(用于生成混淆电路)检查这些打开的电路是否正确构造.如果所有这些电路都是正确的,那么Bob将计算剩余的电路,获得最终输出.这种方法能够迫使Alice正确生成混淆电路,否则Bob将以一定的概率知道Alice进行了欺骗,并终止协议.
在早期的工作当中,这种Cut-and-Choose技术主要用于抵抗恶意敌手实现两方的安全计算.此后,该技术也被用于实现隐蔽安全协议,但并没有引起太多的关注.近年来,随着研究者对于隐蔽敌手的持续研究,该方法或者基于该方法的思想也被广泛应用于实现公开可验证的隐蔽安全协议,涌现出了一些代表性的工作.本文将就这种方法介绍其主要的研究进展以及最新的研究成果.值得指出的是,本文的总结基于前人工作的基础.特别地,文献[15]对基于Cut-and-Choose技术的恶意两方安全计算协议进行了详细的总结和对比,文献[16]在其工作中对Cut-and-Choose技术的研究进展也作了简要介绍.与上述2篇文献相比,本文所涵盖的研究工作更广、更新,重点对近几年热门的公开可验证隐蔽模型相关工作进行了较为详细的分析和总结.
1 基础知识
在介绍基于Cut-and-Choose技术的安全计算协议之前,我们首先介绍相关的基础知识,包括安全模型的定义、茫然传输(oblivious transfer, OT)、混淆电路(garbled circuits, GC)、Cut-and-Choose.
1.1 安全模型
考虑到敌手的存在,MPC的设计目标是,对于给定的目标函数,一组互不信任的参与方只能获得关于各自输入数据的目标函数的正确输出,而不能掌握其他任何信息.一般地,根据敌手的行为,可以将MPC的安全模型分为4种:
1) 半诚实安全.在该安全模型中,被敌手腐化的参与方诚实地遵守协议规定,与诚实参与方共同完成某项计算任务.但同时敌手可以根据其控制的参与方所收到的来自诚实参与方的消息,试图通过观察协议运行中所获得的视图来推断出一些关于诚实参与方私有输入的信息.通常,将这种敌手称为半诚实敌手或者被动敌手,即此类敌手不会采取任何破坏协议的行为.尽管这是一种比较弱的安全概念,但在许多现实应用场景中考虑此类安全模型仍是合理的.
2) 恶意安全.与半诚实敌手相反,在协议执行过程中,恶意敌手(也称为主动敌手)是十分活跃的,可以控制被腐化的参与方任意地偏离协议描述(如发送虚假消息、故意终止协议等),从而破坏协议的安全性.这种能够抵抗恶意敌手的安全模型提供了强大的安全保障,确保任何攻击不会成功.
3) 隐蔽安全.尽管在许多现实场景中,半诚实安全模型是合理的,但是这种安全保障还是太弱.一般来说,如果敌手通过作弊获得的收益远大于实际获得的,那么它更愿意冒被抓的风险而选择作弊.而对于恶意安全模型,尽管具有很强的安全保证,但是效率太低.为了解决这些问题,隐蔽安全的概念被提出.隐蔽安全能保证如果敌手在执行协议时有任何作弊行为,诚实参与方能够以一定的概率发现敌手作弊.并且当这个概率足够大时,对那些企图作弊而又害怕被抓的参与方具有一定的威慑作用,从而能够在一定程度上阻止作弊行为的发生.
4) 公开可验证的隐蔽安全.在隐蔽安全模型中,参与方可以任意偏离协议描述,但会以一定的概率被抓住.这种安全保证比半诚实模型更强.同时,隐蔽安全模型下所设计的协议比恶意安全协议更易于实现,也更高效.然而,隐蔽安全模型仍然有些弱,因为其只对本次协议执行中的敌手具有威慑力.当诚实参与方发现敌手的作弊行为后,可以立刻终止协议来避免损失.但是敌手可以继续选择与其他参与方(如另外一家企业)合作,并试图作弊且有可能作弊成功.因此,Asharov等人[17]提出了具有公开可验证的隐蔽(publicly verifiable covert, PVC)安全模型.在PVC模型中,当作弊行为被发现时,诚实的参与方可以在不泄露私有信息的情况下,公开一份证书用来证实敌手的作弊行为.任何第三方可以检查该证书的有效性.若有效,则会严重影响敌手的声誉,使其失去进一步与其他参与方合作计算的可能.这种公开可验证性极大地增强了隐蔽安全模型的安全性.
1.2 茫然传输
茫然传输(OT)是安全多方计算中的一个基本原语,涉及2个参与方,对安全协议的研究具有重要的作用.本节我们介绍标准的1-out-of-2 OT.发送方Alice拥有2个私有字符串x0,x1;接收方Bob通过自己的选择比特b∈{0,1},选择2个字符串中的1个.在传输完成以后,Bob将获得xb,而不会知道另一个字符串x1-b.同时Alice不会收到任何输出,并且无法知道Bob获得了哪一个字符串.该过程的形象描述如图1所示:

Fig. 1 Illustration of OT图1 OT示意图
更正式地说,1-out-of-2 OT可以写成如下理想功能函数FOT,如图2所示:

功能函数OT该功能函数在发送方Alice和接收方Bob之间运行.输入: ① Alice输入x0,x1∈{0,1}κ,κ表示字符串的长度; ② Bob输入一个选择比特b∈{0,1}.输出: ① Bob输出xb; ② Alice不会获得任何输出.
1.3 混淆电路
1986年Yao[6]基于混淆电路和OT构造了一个通用的安全两方计算协议,称为Yao协议.尽管该协议通信复杂度较高,但是其通信轮数是常数,与电路的深度无关.目前许多MPC协议都是基于姚氏混淆电路构造的.
考虑到任意多项式时间内可计算的功能函数都可以表示成一个布尔电路,在Yao协议[6]中,首先将目标函数F表示成布尔电路C.然后由电路构造方Alice对电路的每一个门进行混淆,即将该门对应的真值表(有4种可能的结果)进行加密并打乱顺序(称之为混淆表),并逐层组合,实现对整个电路C的混淆.最后让计算方Bob逐层计算每个混淆电路门,完成混淆电路C的计算,从而获得函数F的输出.
具体地说,对于电路C中的每条导线w,让Alice生成2个密钥k0,k1(又称为标签),分别对应w上2个可能的值0和1.在执行过程中,根据Alice和Bob的输入,每条导线将与具体的明文值和相应的密钥有关.计算方Bob只知道密钥,而不会知道相应的明文值.例如,对于电路中的一个“AND”门G,如图3所示,有2条输入线wx,wy以及1条输出线wz.wx,wy上的输入分别为u,v(u,v∈{0,1}),wz上的输出为t∈{0,1}.
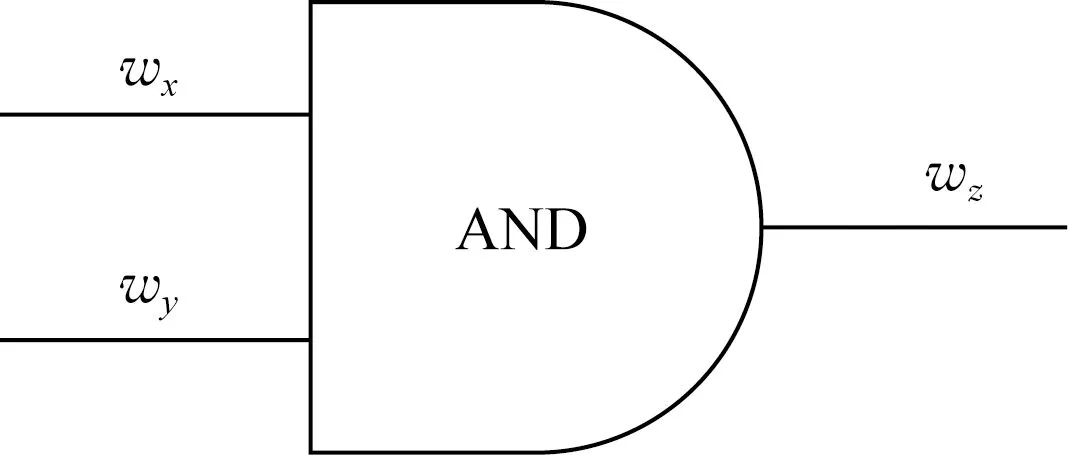
Fig. 3 AND gate图3 AND门

Table 1 Garbled AND Gate表1 混淆AND门
通过对每一个电路门进行表1所示的混淆操作,并逐层组合(前一个门的输出是后一个门的输入),Alice最终能够获得电路C的混淆版本GC.Alice将混淆电路以及自己输入所对应的密钥值发送给Bob.随后,Alice和Bob运行OT协议,茫然地将Bob的输入所对应的密钥传输给Bob.有了每条电路输入线上的密钥值,Bob就可以对混淆电路进行逐层解密,最后获得电路输出线上的密钥,并通过查找表将获得的密钥映射到真实的输出值.
1.4 Cut-and-Choose技术
Yao协议[6]是使用最广泛的MPC协议之一.但是该协议只能实现半诚实安全,不能抵抗恶意敌手的攻击.例如,Alice为了获取Bob的信息,可以选择发送错误的混淆电路给Bob.经典的解决方案是采用GMW编译器[7]的方式,利用零知识证明迫使潜在的恶意参与方诚实执行协议.Alice需要使用零知识证明以证明构造的混淆电路的正确性[7,18].但一般而言,零知识证明需要用到大量的公钥操作,非常低效.另一种实现恶意安全的方法是采用“MPC-in-the-head”技术[19-21],参与方通过模拟一个虚拟的诚实方大多数的多方协议来保证安全性[21-22].由此设计出来的协议具有渐进的复杂度,但协议整体的效率依赖于被模拟的安全多方协议和模拟该多方协议的半诚实协议,并且目前还没有任何实例给出这种方法在实际应用中具体的时间复杂度[14].Lindell等人[23]提出将SPDZ协议[24]作为外部协议生成混淆电路,但没有给出实例化的方案.Nielsen等人[25]通过为各参与方持有的秘密信息份额添加信息论安全的MAC以实现认证通过的AND门和OT协议,从而防止不诚实的参与方进行作弊,由此设计出通信复杂度与电路深度成正比的TinyOT协议.
为了能够有效抵御恶意敌手的攻击,同时提高协议的效率,基于Cut-and-Choose技术被提出[8].该技术主要用于安全两方协议,确保其中一方此前收到的来自另一方的消息是遵循协议规范正确构造的.早期工作中这种方法也被广泛与交互式证明[26]、零知识协议[26-28]、证据不可区分以及证据隐藏协议[29]进行结合.其主要思想是,一方在协议执行过程中对发送的消息生成多个副本,另一方通过随机选择其中一部分进行检查保证消息的正确性.一旦检查通过,剩余的消息将参与协议的后续阶段.这种思想最早可以追溯到文献[30],用于盲签名的实现.该技术应用于混淆电路的具体过程为:
1) Alice首先选取s个随机种子,利用这些种子生成s份独立的混淆电路GC,每一个电路用于表示相同的目标函数F,其中s称为电路复制因子.然后Alice将所有的电路和与其输入线相关的密钥发送给Bob.
2) Bob随机选取一部分电路I⊂{1,2,…,s},作为检查电路.对于每一个电路j∈I,Bob要求获取Alice的随机种子seedj,从而得到电路中每条线上的2个密钥(分别对应数值0和1),用于打开电路GCj进行检查,验证GCj是否构造正确,即GCj是否是电路C的正确混淆版本.
① 如果所有的电路构造正确,Bob按照Yao协议[6]独立地计算I以外的剩余电路(称为计算电路).
② 如果至少有一个电路是错误的,那么Bob知道Alice是不诚实的.考虑到让Bob直接终止协议可能会带来安全性问题,不同的方案中规定Bob此时会有不同的处理,我们将在后续章节进行详细介绍.
Cut-and-Choose技术能够有效抵御恶意的Alice构造错误的电路,即Alice作弊会以很高的概率被Bob检测到,但该方法同时也引入了2个重要的安全性问题——输入一致性问题以及选择失败攻击问题.参与方可以在不同的混淆电路中提供不同的输入,获取不同的输出,从而推断出与对方输入数据相关的信息.此外该方法并不能确保所有未被打开的电路是正确的,因为每一个电路都是以1/2的概率被检查.Bob可能从计算电路中获得多个不一致的输出,这种情况下它将知道Alice在作弊.如果Bob选择终止协议,可能会泄露信息,因为Alice可以事先猜测Bob在OT协议时的输入故意使用错误的密钥(选择失败攻击).例如,在OT协议执行中,Alice使用正确的密钥值作为Bob输入第1位为0所对应的消息,而使用一个与混淆电路中真实使用的密钥不同的随机数作为Bob输入为1所对应的消息.之后Alice通过观察发现如果Bob没有终止协议,则说明Bob的第1位输入为0;若其终止了协议,则说明Bob的输入为1.
为了解决这个问题,一般将计算电路的大多数输出值作为最终的计算结果.此时,如果所有的检查电路都是正确的并且大多数计算电路是错误的,那么认为Alice作弊成功.在基于Cut-and-Choose技术设计MPC协议时,如果Alice成功作弊的概率可以忽略(即达到统计安全级别2-40),我们就认为该协议是安全的,通常达到统计安全级别与s的选取、被检查的电路个数以及每个电路被检查的概率与策略有关.
与使用零知识证明(低效的非对称操作)实现恶意安全相比,Cut-and-Choose技术可以有效提高协议的效率.同时,从协议整体运行时间以及目标函数表示成布尔电路等情况出发,在混淆电路上进行Cut-and-Choose技术依然是抵御恶意敌手的最有效方式.值得注意的是,近年来,Wang等人[31]提出了一种新型高效的构造恶意安全协议的方法Authenticated-GC,只需要构造一个经过认证的混淆电路,就可以完成对目标任务的计算,并且具有常数轮复杂度.之后在2018年,他们又提出了优化方案[32],进一步提高了通信效率.
鉴于Cut-and-Choose技术在恶意敌手场景中具有良好的表现,因此,早期大部分的工作将该方法应用于恶意两方安全计算,但是完全的恶意安全模型难以实现、效率低.此后,相继有相关工作在隐蔽模型下使用Cut-and-Choose技术,但是没有引起太多关注.而随着近年来研究者对隐蔽敌手的深入研究,许多结合Cut-and-Choose技术实现PVC模型的优秀工作不断涌现.下面,我们将从Cut-and-Choose技术分别应用于恶意模型、隐蔽模型以及PVC模型3个不同的场景对相关领域的研究工作进行介绍.
2 基于Cut-and-Choose技术的恶意安全协议
在利用Cut-and-Choose技术抵御恶意敌手时,一个主要的挑战是如何最大程度将电路复制因子s降低,从而用更少的混淆电路来达到概率为2-40的统计安全级别.如1.4节所述,一种经典的做法是让计算方Bob计算多个电路,并取电路计算结果中占大多数的输出值作为最终输出.后来又涌现了许多工作对这一做法作出改进,设计了多种不同的安全协议.我们把这些相关的工作分为4类:
1) MajorityCut.根据所选择的计算电路,让Bob将所有计算电路输出值中的大多数结果作为最终的输出,使得Alice只能够以可忽略的概率成功作弊,从而保证协议输出的正确性.
2) SingleCut.在所有未打开的计算电路中,即使只有一个计算电路是正确的,也能够保证Bob可以获得正确的协议输出.
3) BatchedCut.这种方法将Cut-and-Choose技术应用于多个安全计算实例中,即参与双方通过不同的输入安全地计算目标函数F多次,在每次安全计算中,要求电路构造方Alice构造多个混淆电路以应用Cut-and-Choose技术,保证电路正确的同时又能够获得良好的分摊效率.
4) Gate-LevelCut.与将Cut-and-Choose技术应用到整个电路不同,这种方法在电路的门上进行Cut-and-Choose技术.Alice生成许多个混淆门并发送给Bob,然后Bob要求Alice打开一部分混淆门进行检查;检查通过后,Bob由剩余未打开的混淆门构造出要计算的目标电路.
下面我们详细介绍4种方法相关的研究成果.
2.1 MajorityCut
为了避免低效的零知识证明操作,同时又能够抵抗恶意敌手的攻击,Pinkas[8]将Cut-and-Choose技术引入到基于混淆电路的安全两方计算中,并通过盲签名[33]和定时承诺[34]来保证协议的公平性.在该方案中,要计算的目标函数F(x,y)=(FAlice(x,y),FBob(x,y)),FAlice(x,y)表示Alice的输出,Bob的输出为FBob(x,y).Alice首先为目标函数构造一部分混淆电路,并连同承诺过的输入线上的密钥一起发送给Bob.为防止Alice恶意构造错误的电路,Bob随机选择一半电路,要求Alice打开对应这些电路的每一条输入线的2个密钥(对应0和1)的承诺以及对随机数k的承诺(k用于决定混淆表中输出结果的位置).根据这些信息,Bob可以验证这些打开的电路能否正确地计算目标函数,若这些电路中有任何一个是错误的,则Bob终止协议.一旦验证通过,Bob可以对剩余的电路进行计算,将计算电路中占大多数的输出结果返回给Alice.同时为了防止Bob发送错误的输出结果给Alice(反之亦然),导致协议的不公平性,文献[8]要求双方基于另一方的密钥对各自获得的输出结果进行承诺,并采用盲签名验证所承诺的内容的正确性来解决这一问题.与基于零知识证明的工作相比,由于混淆电路的检查和计算都是高效的对称加密,因此利用Cut-and-Choose技术可以有效地提升协议的效率[15].
2006年Kiraz等人[35]指出,尽管文献[8]可以保证协议输出的公平性,但仍然是不安全的,在OT协议执行过程中容易遭受选择失败攻击(如1.4节所述).而为了抵抗这种攻击,他们提出采用committed OT技术,保证任何试图使用错误信息代替OT协议正确输入的行为都将会被Alice发现而终止协议.然而,与标准OT相比,committed OT的效率比较低.
同年,文献[36]基于Pedersen承诺提出了2种不同的解决方案以克服Fairplay协议[37]存在的缺陷,即一方作弊而不被发现,例如Alice可以通过改变1-out-2-of OT协议的2个输入密钥的顺序进行攻击.但是该工作要求只有Bob可以获得输出,并且Alice依然可以在OT协议中故意构造错误的输入来获取Bob的隐私信息.此外,由于采用大量的承诺操作来保证Alice对于不同的电路使用相同的输入,这项工作的通信代价过高,需要传输承诺的数量为O(n2s+|C|s),n是电路C的输入长度,|C|是电路的大小.后来在2007年欧密会上,Woodruff[38]对此进行了改进,将通信开销降至O(|C|s).
同年,Lindell等人[11]指出将Cut-and-Choose技术和Yao协议[6]简单地结合并不一定能得到一个恶意安全的协议.于是,在他们的工作中,合理地结合两者实现了高效的恶意两方安全计算协议,与半诚实的Yao协议[6]几乎具有相同的计算开销,并基于理想/现实模拟范例给出了完整的安全证明.他们将Cut-and-Choose技术应用于整个电路以及输入(用于保证Alice输入的一致性),并选择打开一半的电路进行检查,如图4所示.在这种情况下,恶意的Alice成功欺骗Bob接受一个错误输出的概率为2-s/17.因此他们的协议至少需要构造680个混淆电路实现概率为2-40的统计安全.另一方面,由于需要发送O(sn2)个承诺,n是Bob的输入长度,这项工作的通信开销过高.

Fig. 4 Overview of reference [11] protocol图4 文献[11]协议的简要描述


Cut-and-Choose技术功能函数ccot该功能函数在发送方Alice和接收方Bob之间运行.输入: ① Alice输入一个向量x={(x0i,x1i)}si=1; ② Bob输入σ1,σ2,…,σs以及大小为s∕2的集合P,P⊆{1,2,…,s}.输出: ① 对每个j∈P,Bob获得(x0j,x1j); ② 对每个j∉P,Bob获得xσjj; ③ Alice不会获得任何与σ1,σ2,…,σs以及集合P有关的信息.
简单地说,对于所有的检查电路中Bob的每条输入线,Bob可以得到密钥对中的全部2个密钥;而在计算电路中,Bob只获得与其选择比特σ相对应的密钥.利用该原语,文中将抵抗选择失败攻击与电路检查这2部分进行了融合,在有效检测敌手是否作弊的同时降低了协议通信复杂度.进一步,他们的工作放弃对电路的承诺,通过适当增加指数运算(需要O(sn)次模幂操作),减少了通信代价,并结合高效的零知识证明以验证Diffie-Hellman元组,将输出错误的概率降到了2-0.311s,与文献[11]相比,该方案只需要构造128个混淆电路就可以保证协议输出的正确性.但与文献[11,39]中抵抗选择失败攻击的方法相比,Cut-and-Choose OT效率并不具有优势.
文献[13]则通过检查60%的电路进一步地将这个概率减小到了2-0.32s.同时,该项工作还指出,假设计算电路和检查电路开销相同,为了获得2-ρ的统计安全(ρ是统计安全参数),至少需要ρ≈3s个电路.这意味着,对于2-40的错误概率,仍然需要构造125个电路.如果电路的规模巨大,协议依旧会比较低效.
2017年赵川等人[40]指出文献[14]基于Cut-and-Choose OT设计的安全两方计算协议由于密钥的传输被分割成几个阶段,导致参与方之间的交互依然复杂,不易理解和应用.因此,他们提出了双向Cut-and-Choose OT,要求Alice增加2个输入字符串,以赋予Alice主动选择权,而不是仅仅输入密钥对等待Bob进行选择.Alice可以通过1个比特决定Bob接收其输入的2个密钥中的哪一个,同时Bob依然能够根据其指示比特j决定获得1个密钥还是2个密钥.这种双向性使得所有的密钥可以在同一阶段全部传输完成,显著地降低了Alice和Bob之间的交互轮数.为了与文献[14]中的单向OT协议进行更加直观的比较,考虑上述双向OT协议批处理的版本,通过功能函数Fccbot进行表述,如图6所示:

Cut-and-Choose Bilateral OT功能函数ccbot该功能函数在发送方Alice和接收方Bob之间运行.输入: ① Alice输入向量x={(x0i,x1i),(y0i,y1i),bi,τi}si=1,bi是置换比特,bi∈{0,1},τi是选择比特,τi∈{0,1}; ② Bob输入σ1,σ2,…,σs以及集合P,P⊆{1,2,…,s}.输出: ① 对每个j∈P且j=1,Bob获得{(xbij,x1-bij),1-bi,(y0i,y1i)}; ② 对每个j∉P,Bob获得(xτjj,yσjj,τj⊕bj),τj⊕bj指示xτjj的位置; ③ Alice不会获得任何与σ1,σ2,…,σs以及集合P有关的信息.
2.2 SingleCut
在MajorityCut方法中,总是选取一定数量的电路进行检查(如s/2),根据检查电路和计算电路的划分,以及接受计算电路输出的大多数结果,能够将恶意的Alice成功作弊的概率降到2-ks,k∈(0,1].然而,与此同时,该方法要求Alice必须向Bob证明在所有的计算电路中其提供了相同的输入,由此带来了额外的开销.
在2013年美密会上,Lindell[41]对文献[14]提出的Cut-and-Choose OT进行了改进,允许Bob以1/2的概率独立地检查任意数量的电路而不是选取一半的电路打开检查.他的这项工作在仅构造s个混淆电路的情况下,就能保证敌手成功作弊的概率为2-ρ,打破了文献[13]指出的至少需要3s个电路的限制.即对于2-40的错误概率,该工作只需要构造40个电路.其背后思想是:当且仅当所有打开的电路都是正确的且所有的计算电路都是错误的时候,Alice才可以作弊成功.
具体而言,他将整个协议的构造分为2个阶段进行.在第1阶段,电路构造方Alice首先生成s个混淆电路,每个电路以1/2的概率被独立地选择作为检查电路或计算电路.令x1,x2分别是Alice和Bob的输入,对于所有的计算电路,如果Bob计算得到同样的输出F(x1,x2),那么Bob将F(x1,x2)存储在本地;否则,根据事先约定,Alice为所有电路中的输出线分配相同的输出密钥,因此Bob可以在本地存储一个“proof”,用于证明2个计算电路的不同输出——同一输出线上对应2个不同的输出密钥.
在第2阶段,参与双方安全地计算一个“惩罚函数”.如果Bob接收到的输入不一致,则其将“proof”作为输入,通过“惩罚函数”,Bob将获得Alice的真实输入,从而在本地再次计算电路获得输出.否则,Bob将F(x1,x2)以及一个随机数作为输入,在这种情况下,Bob不会从惩罚函数的计算中收到任何有用信息.注意这里之所以让Bob即便在没有获得“proof”的情况下依然需要和Alice运行“惩罚函数”,是因为如果2种情况下Bob的行为有区别,则Alice完全可以得知Bob是否在不同的计算电路中获得了不同的输出,而这样是会泄露Bob的输入信息的.
同年,另一项工作[42]基于文献[43]中两方对称构造混淆电路的思想,提出使用对称Cut-and-Choose技术来抵抗恶意敌手的攻击.在这项工作中,要求每一方构造s个混淆电路,由另一方检查部分混淆电路的正确性,一旦检查通过,双方计算各自的剩余电路,然后根据计算结果,决定电路的最终输出值.进一步地说,对于混淆电路中某一条输出线,如果一方在其生成的至少一个计算电路的输出线上获得输出v,并且另一方的计算电路中也存在这种情况,那么该参与方在这条输出线上的最终输出就是v.这种情况下,由于一方是诚实的,其构造的所有电路都是正确的,此时只要另一参与方提供的计算电路中至少有一个是正确的,就能保证目标电路的正确性.当检查s/2个电路时,该工作确保敌手仅能以2-s+O(log s)的概率成功作弊.然而,由于每一方都需要构造混淆电路,在协议中被发送的电路数量是以往工作的2倍.
此外文献[44-45]分别采用不同的方法,同样保证了只需要s个电路,就能将输出错误的概率降到2-s.这些工作均确保不诚实的Alice只有在所有的计算电路不正确的情况下,才能破坏协议的安全性.
2.3 BatchedCut
Cut-and-Choose技术引入的开销主要与构造以及发送的混淆电路数量有关.通过2.2节的方法,尽管只需要构造s个混淆电路就能将敌手成功作弊的最大概率限制为2-s,但如果要计算的电路规模巨大,发送s个混淆电路,仍然会带来不小的开销.并且在实际应用中,往往需要双方共同参与某项计算任务多次,而每次只是输入不同.此时,如果每次仍然继续构造s个混淆电路以保证计算的正确性,不仅需要生成大量的电路,并且是不高效的.因此,BatchedCut方法被提出.其基本思想是首先由Alice生成一些电路,经Bob选择打开其中一部分进行检查后,Bob将剩余的电路随机组合分成若干组.每组中的电路用于执行一次协议,这样在若干次执行(具有不同的输入)以后,由于全部的电路可以分摊到每次执行当中(每次计算需要构造的混淆电路数量将小于s),因此,这种方法可以有效地分摊Cut-and-Choose技术带来的开销.

Huang等人[47]结合“LEGO” Cut-and-Choose[48]和Fast Cut-and-Choose[41],采用不同的方法运行安全协议多次来保证电路的正确性,每次执行只分摊较低的开销.具体来说,他们将整个过程分为2个阶段.在第1阶段,将“LEGO” Cut-and-Choose技术应用在电路级别(而不是电路门级别),即Alice构造许多个混淆电路并发送给Bob,然后Bob要求Alice随机打开一部分电路进行检查.如果没有检查到错误的电路,就执行第2阶段.Bob将未打开的电路分到多个桶中,对每一个桶执行Fast Cut-and-Choose技术[41].他们的方法保证了即使每个桶中只有一个电路是正确的,协议的安全性也不会被破坏.

2015年文献[49]提出了一种新的方法来保证Alice在所有的混淆电路中使用相同的输入,只需要对每个电路而不是每个输入比特[39,50]执行O(s)次对称加密操作,并且在离线/在线场景中,由于需要构造的混淆电路的数量小,这种方法产生的开销也比较低.此外,这项工作还采用了文献[39]中抵抗选择失败攻击的方法,对文献[46]中基于离线/在线范例的协议进行了优化和实现,进一步减小了在线阶段的通信开销.
2.4 Gate-LevelCut

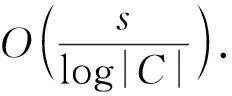
至此,我们给出了基于Cut-and-Choose技术的恶意安全两方计算的经典工作.表2展示了主要的恶意安全两方计算协议的各项对比.

Table 2 Comparison of Secure Two-Party Computation Protocols Against Malicious Adversary表2 恶意两方安全计算协议对比
3 基于Cut-and-Choose技术的隐蔽安全协议
3.1 相关背景
在针对半诚实敌手的模型中,安全计算可以非常高效地执行,但是协议的安全性却不令人满意.半诚实模型能够保证的是,如果所有的参与方都遵守协议规范,那么就可以实现安全性.而针对恶意敌手的安全协议能够提供非常强大的安全保障.但是这样强大的安全保证是有代价的,一般而言,恶意安全协议比半诚实安全协议要慢几个数量级[25].
为了权衡效率和安全性,Aumann等人[54]在理想/现实模拟范例下,根据敌手的能力,给出了2种针对隐蔽敌手的安全性定义,即可以保证:如果敌手试图作弊以破坏协议的某些安全属性(正确性、隐私性、输入独立性等),那么诚实的参与方能够以一定的概率ε(ε称为威慑因子)检测到敌手的欺骗行为.对于敌手的这种欺骗能力,粗略地说,即如果敌手在理想模型下,除了获得正常的输出以外,还知道一些有关诚实方输入的信息,那么它就成功地进行了欺骗.
事实上,赋予敌手这种欺骗能力的思想早在文献[37,55-57]中已经提及,但是他们的工作并没有作出形式化的说明和定义.其中Malkhi等人[37]提出的方案和目前抵御隐蔽敌手的工作思想上基本一致.由Alice向Bob发送s个混淆电路,然后Bob随机选取1个电路作为计算电路,验证剩余s-1个电路是否确实可以表示目标函数.这种方法允许Alice发送错误的电路而不会被发现的概率最大为1/s.而文献[56]只考虑诚实方占大多数的情况,并且对于安全的定义没有遵循模拟范例.但Aumann等人[54]引入的隐蔽敌手的概念加强了他们的工作,而且能够量化所有可能的敌手(而不是以某种特定策略执行协议的敌手)[58].
无论恶意敌手或者隐蔽敌手,Cut-and-Choose技术都是一种高效的编译技术,针对这2种敌手的工作也有些相像,但同时又有所不同.在应用Cut-and-Choose技术抵抗恶意敌手攻击时,要求诚实的参与方确保另一方作弊的概率要足够小;而面对隐蔽敌手,要求诚实的一方在敌手试图欺骗时,能够以较大的概率检测到这一作弊行为,在起到对敌手有一定威慑作用的同时,不显著影响协议的效率,使得隐蔽安全协议比恶意安全协议更高效.下面我们将对隐蔽敌手模型的相关成果进行简要介绍.
3.2 研究工作
在TCC 2007会议上,Aumann等人[54]基于Cut-and-Choose技术对Yao协议[6]进行了修改,要求发送s份混淆电路,然后打开s-1份电路,以检查电路构造是否正确.同时为了避免选择失败攻击,将计算方Bob的每个输入位扩展为m位的异或,最终实现了具有威慑因子ε=(1-s-1)(1-2-m+1)的隐蔽安全两方协议.这种对安全模型的放松使得协议设计者能够构造高效的协议,并且与半诚实协议的效率只有很小的差距.
在文献[54]工作的基础上,文献[58]基于BMR协议[59]设计出非诚实方占多数的具有隐蔽安全的多方协议,并且敌手只能以1/s的概率欺骗成功.然而该工作要求大量的承诺操作,通信代价过高.对于电路规模为|C|的布尔电路,需要传输的比特数量为O(n3sρ|C|),ρ是统计安全参数.
之后Damgård等人[60]提出采用编译器的方法将半诚实安全的协议转换成隐蔽安全的协议,不同于文献[58],他们的方案要求诚实方占大多数.尽管他们并没有直接利用Cut-and-Choose技术结合混淆电路来检测敌手的作弊行为,但是思想是一致的.具体来说,他们利用Shamir秘密共享技术为半诚实安全协议准备2组输入,一组是真实的输入,一组是错误的输入,这些输入都是以份额的形式存在.各个参与方并不知道自己所拥有的份额是否是错误的.然后,在2组输入上分别运行半诚实安全协议,直到各方持有输出份额.通过揭示哪些输入份额是错误的,参与方在包含该输入份额的执行中,使用与该执行相关的所有信息来检查是否存在作弊行为.如果没有,接受包含真实输入执行的输出.最终他们的协议能够以1/4的概率抵抗隐蔽敌手的攻击.但是由于为半诚实安全协议提供了2组输入,如果没有检测到欺骗的话,他们协议的成本基本上是原来协议的2倍.
在2013年美密会上,Lindell[41]基于Cut-and-Choose OT实现了恶意安全的同时,对恶意安全协议进行了修改,能够以ε=1-2-s+1的概率抵抗隐蔽敌手的攻击.即如果检查电路中至少有一个是错误的,那么Bob将声明Alice被敌手腐化进行了作弊,而不是终止协议.而对于所有的检查电路都构造正确但存在2个电路输出不一致的情况,Bob只需要在第2阶段获得Alice的输入x1,本地计算获得正确的F(x1,x2).
4 基于Cut-and-Choose技术的PVC安全协议
4.1 相关背景
隐蔽安全模型的提出具有一定的实际意义,在某些情况下,敌手被发现作弊所造成的声誉损失大于不被发现所带来的收益.因此,它能劝阻那些关心自己声誉、不想冒险被发现作弊的隐蔽敌手.因而隐蔽安全比半诚实安全提供了更强的安全保障,同时与恶意安全相比,它也能实现更高的协议效率[14,39,58].
但是,隐蔽安全模型的安全性从某种意义上来说还是不够强.具体说来,如果电路构造方Alice试图作弊,协议能够保证她被计算方Bob以一定的概率抓住,因此Bob就会知道Alice是不诚实的,但Bob并不能说服第三方Alice存在作弊行为,因为他并不掌握任何Alice作弊的证据.为了解决该问题,Asharov等人[17]提出了一个更强的安全模型——公开可验证的隐蔽(PVC)安全模型.它能确保在检测到敌手欺骗的情况下,诚实的一方通过blame算法计算出一个公开可验证的证书,任何第三方可以利用judge算法,将该证书作为输入,验证证书的有效性,从而检查被指控方是否确实进行了欺骗.
4.2 具体的PVC协议设计
为了给出PVC模型下的一个安全协议构造,Asharov等人[17]对文献[54]的工作进行了修改,要求双方对交换的信息进行签名,并用所提出的新原语——signed-OT(签名OT)代替标准OT,实现了具有公开可验证的隐蔽安全两方计算协议.该协议几乎与不具有公开可验证性的文献[54]具有同等的效率.
具体来说,在该协议中,首先由Alice生成s个混淆电路,并对这些电路进行承诺后发送给Bob;经过signed-OT协议,Bob可以获得在每个电路中对应其输入的所有被签名的密钥.如图7所示,Alice输入(x0,x1)和一个签名密钥sk,Bob输入一个随机比特b,协议执行结束后,Bob将获得签名消息——(xb,Signsk(b,xb)).这保证了如果Bob探测到了任何Alice的欺骗行为,由于它在一组不一致的消息上拥有Alice的签名,这便可以作为Alice欺骗的证据.通过一个1-out-of-ssigned-OT运行Cut-and-Choose技术,Bob能够获得要打开的s-1个检查电路的信息以及对这些信息的签名,从而检查这些电路是否构造正确.同时,由于Alice并不知道Bob对于检查电路的选择(由signed-OT保证),Alice无法因被检测到其作弊而提前终止协议.如果没有检测到欺骗,Bob向Alice揭示其选择的计算电路标识.相应地,Alice发送对应该标识的混淆电路和其输入密钥,Bob根据这些密钥可以对该电路进行计算获得输出.

signed-OT功能函数sigot该功能函数在发送方Alice和接收方Bob之间运行.输入: ① Alice输入(x0,x1,sk),sk是签名私钥; ② Bob输入(vk,b),vk是验证签名的公钥.输出: ① 计算σ=(xb,Signsk(b,xb)),若Verifyvk((b,xb),σ)=1,Bob获得σ;否则,终止协议; ② Alice不会获得任何输出.
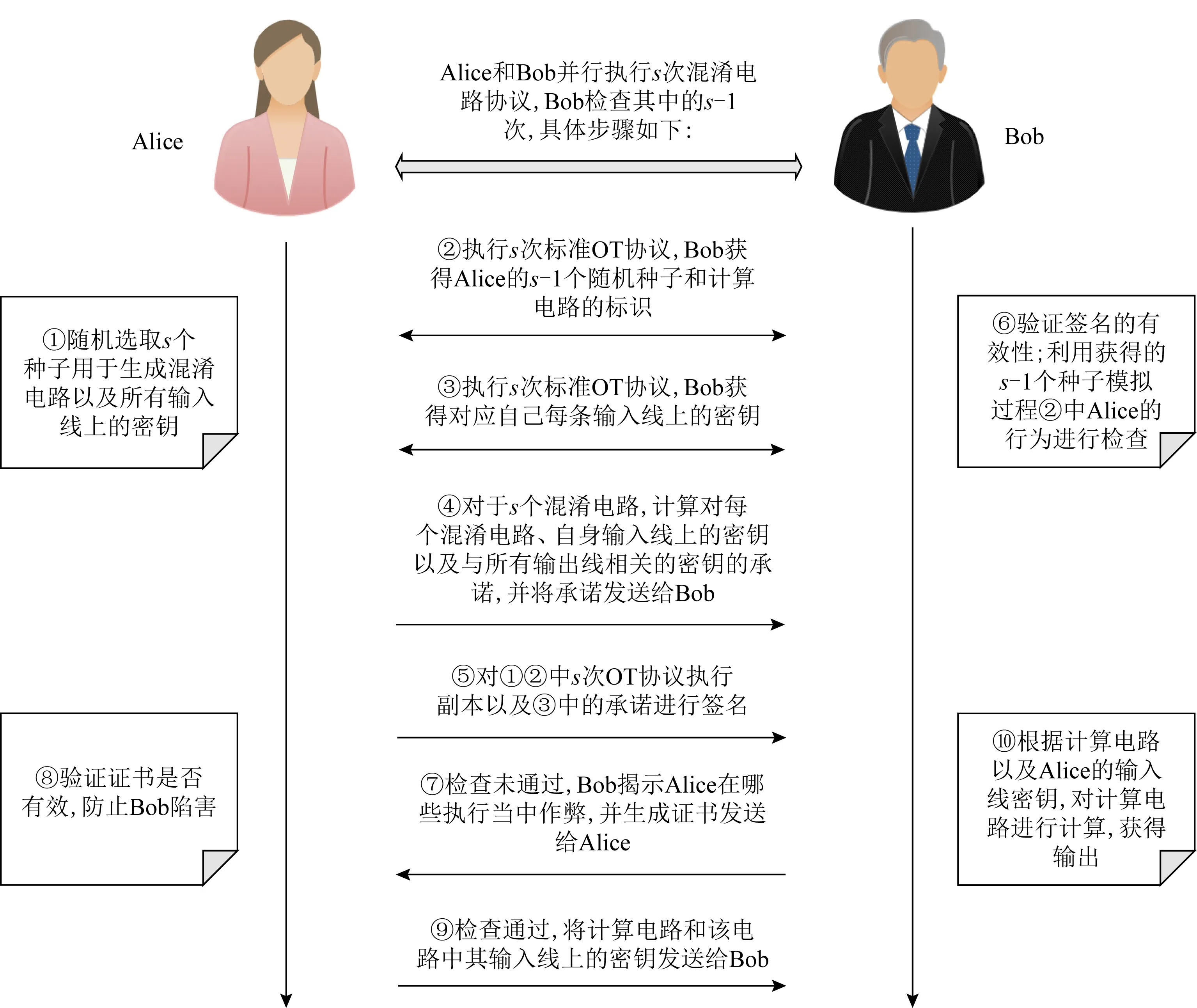
Fig. 8 Overview of reference [62] protocol图8 文献[62]协议的简要描述
signed-OT需要大量的公钥操作,代价昂贵.并且在Asharov等人[17]的方案中,为了避免Alice进行选择失败攻击,采用XOR-tree技术将计算方的每个输入比特扩展为m位异或的方式(增加了输入的长度,需要额外的signed-OT),这对效率有很大的影响,因为每个输入比特都需要执行一次OT协议.当每个输入比特被分成m个份额时,每个输入比特将需要m次OT协议.此外,这种方式对威慑因子ε的大小也会产生影响.
在2015年亚密会上,Kolesnikov等人[61]基于文献[12]的工作提出使用signed-OT扩展代替signed-OT的思想来减少公钥操作,从而实现了协议效率的改进,但这并不适用于小规模电路.而且,该方案依然采用XOR-tree技术来避免选择失败攻击,为了实现较大的威慑因子,不得不引入额外的开销.
Hong等人[62]在2019年欧密会上,采用标准OT,提出了一个新的公开可验证的隐蔽安全协议,简单且开销低,避免了昂贵的signed-OT,同时放弃了XOR-tree技术,降低了计算复杂度,并实现了常数大小的验证证书.
在他们的方法当中,Alice随机选择s个随机种子,用于生成s个混淆电路.这些种子不仅决定了混淆电路和承诺的生成,而且用于OT协议中来传输Bob的输入密钥.这意味着Bob通过标准OT茫然地获得一个种子后,Alice的执行对Bob来说就是确定性的.此后双方执行一个具有恶意安全的OT协议s次,允许Bob获得s-1次执行中Alice使用的随机种子和计算电路的标识.
同时,Alice需要对所有的混淆电路以及OT协议的执行副本进行签名,然后发送给Bob.根据这些随机种子,Bob可以模拟OT协议执行和混淆电路的生成,如果模拟的结果与之前收到的结果不一致,Bob将输出证书(该证书包含有Alice签名的OT协议执行副本、GC协议执行副本以及随机种子)作为Alice欺骗行为的证据.如图8所示,我们给出整个协议的大致描述.
与文献[17,61]的工作相比,标准OT比signed-OT更简单,而且signed-OT在通信和计算方面都比标准OT有更高的成本.此外,文献[62]的工作实现了证书大小与电路规模和参与方的输入长度无关.为了防止Alice发送错误的输入密钥,文献[61]中要求Alice对这些密钥进行承诺,但该工作避免了这一要求.我们在表3中给出了文献[17,61-62]的通信复杂度对比.
宏观上看,文献[62]的工作采用更为简单的标准OT,降低了计算开销,常数大小的证书减小了通信成本.但是在检查协议执行中Alice是否有欺骗行为发生时,要求Bob本地再次模拟执行s-1次OT协议,将模拟的结果与实际得到的输出进行比较,计算方开销较高,并且在验证证书的合法性时,也需要Bob完全模拟一次OT协议的执行.

Table 3 Comparison of Communication Complexity of Different PVC Protocols表3 不同PVC协议的通信复杂度对比
在CCS 2019会议上,Zhu等人[63]将敌手的收益/损失考虑在内,提出一个新的安全概念——Financial Security.同时他们指出,现有的PVC协议关注的重点不是judge算法的复杂性,而是使用一个整体的算法来执行大量计算.对此,他们将公开可验证的隐蔽安全计算与一个高效的、去中心化的judge算法(由以太坊智能合约实现)相结合,实现了具有Financial Security的两方计算协议.
在他们的方案中,通过调用s-1次Sender Non-Repudiable OT(发送方不可否认OT,和signed-OT具有同样的功能),Bob能够获得用于生成所选择的s-1个检查电路的随机种子,实现了威慑因子ε=1-s-1.与传统的安全两方计算定义相比,新的安全概念将各参与方的收益/损失进行了量化,减少了复杂密码学操作的数量.与文献[62]的工作不同的是,电路计算方Bob的“负担”较轻,不需要完全模拟一次OT协议的执行,并且judge算法不要求敌手的参与,也不需要知道计算所用的秘密输入,可以实现完全去中心化.
如表4所示,我们给出了文献[17,61-63]中4项工作使用不同的OT协议所引入的带宽开销.

Table 4 Comparison of Communication Complexity of Different OT Protocols表4 不同OT协议的通信复杂度对比
4.3 采用编译器实现PVC协议
为了实现某种安全模型下的协议构造,一种方法是直接构造满足该安全模型的具体安全协议,另一种方法是使用编译器,将安全性较弱的协议转换为安全性较强的协议.与具体协议相比,编译器的主要优势在于,即使未来有新的高效方法可以实现半诚实安全协议,但只要该协议满足编译器的转换要求,它也能通过编译器被转换成具有更强安全保证的协议,而不再需要继续基于这种方法尝试构造出更强安全保障的协议.
2020年美密会,Damgård等人[64]构造了2个编译器将半诚实安全协议转换成公开可验证的隐蔽安全协议.该工作采用离线/在线结构,将协议分成预处理阶段(Πoff)和在线阶段(Πon).离线阶段与私有输入无关,用于生成相关随机性,例如混淆电路、乘法三元组等.而在线阶段利用这些相关随机性和参与方的私有输入来计算目标函数.他们通过第1个编译器实现了一个具有公开可验证的隐蔽安全预处理协议,然后结合第2个编译器,将带私有输入的协议由半诚实安全性编译成公开可验证的隐蔽安全性.同时,在该项工作中,离线/在线的设置能够有效地应对Cut-and-Choose技术所面临的挑战:在适当的时机打开电路进行检查.因为如果过早地打开电路,则在协议的后续阶段可能会发生欺骗;而如果未能及时打开电路,那么可能会泄露诚实参与方的输入信息.
具体地说,他们的工作延续了Cut-and-Choose技术的思想,在设计第2个编译器时,采用“MPC-in-the-head”/“watchlist”技术.Alice和Bob分别有m个虚拟方,将自己的私有输入分享给各自的m个虚拟方.所有的这些虚拟方联合执行半诚实安全协议Π.在协议执行期间,Alice和Bob代表他们模拟的虚拟方发送消息.如果任何一个真实的参与方(Alice或Bob)存在欺骗行为,那么必然会在至少一个虚拟参与方中产生该作弊行为.通过让Alice和Bob各自检查彼此的部分虚拟方,来检查协议执行过程中是否存在欺骗.假设Alice得到了Bob的q个虚拟方的输入和随机种子,Alice就可以重构出这些虚拟方本应该发送的消息.由于Bob不知道检查了哪些虚拟方,任何欺骗行为都将以q/m的概率被发现.
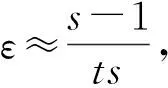

Table 5 Comparison of Deterrence Factor ε in Pre-processing Protocols表5 预处理协议中威慑因子ε的比较
对此,在Faust等人[65]的工作中,引入了一种新的机制——time-lock加密[66],将time-lock加密结合可验证延迟函数[67]来实现公开可验证.time-lock加密背后的思想很简单,可以理解为将秘密放在拼图(puzzle)中,只有在一段固定的时间以后,成功完成拼图,才能获得秘密.具体而言,在执行半诚实安全协议时,他们的方案要求利用time-lock加密对所有参与方的随机字符串r(用于选择打开部分半诚实协议实例)、随机性u(生成puzzle)以及随机种子进行加密.即使被腐化的参与方恶意终止,通过完成拼图,诚实的参与方也能获得随机种子而不需要与敌手进行交互.然后,诚实的参与方基于这些种子模拟所有的参与方并运行除第r次以外的s-1次半诚实协议,来检查是否有欺骗行为发生.
尽管采用time-lock加密引入了额外的开销,但是另一方面由于其独立于半诚实协议的复杂度,因此可以分摊该开销.与文献[64]相比,time-lock加密能够确保总有一次半诚实协议执行没有被检查,这提高了威慑因子的大小.
Scholl等人[68]指出文献[58]的工作并不满足标准安全的定义,无法实现可识别欺骗(一种安全性质),即不能够允许所有诚实的参与方统一意见,一致认同不诚实的参与方存在欺骗行为.因此,他们首先提出第1个编译器,将半诚实安全的预处理协议转换成具有可识别欺骗和可识别终止性质的隐蔽安全协议.为了获得公开可验证性,同时防止敌手通过伪造证书陷害诚实的参与方,他们引入了一个新的概念——公开可验证作弊(public verifiable cheating),能够正确地标识被敌手腐化的参与方,即使该参与方没有做出试图获取秘密信息的行为,但在协议执行过程中提前终止协议.同时,为防止在检查协议执行时敌手事先知道诚实参与方掌握了对其不利的信息而提前终止协议,要求所有的参与方本地生成time-lock puzzles,迫使被腐化的参与方在无法获知是否欺骗成功的情况下对要打开的协议执行进行承诺.而文献[65]则需要利用一个恶意安全的MPC协议来生成puzzles,这引入了额外的开销,且敌手可以从预处理协议获得输出后进行欺骗.
最后,Scholl等人[68]将所提出的编译器应用于BMR协议[59]、SPDZ协议[24,69]进行实例化,得到了可以抵御任意数量的恶意参与方攻击的公开可验证的隐蔽安全协议.
表6给出了对基于Cut-and-Choose技术/思想的各PVC协议的总结对比.图9给出了基于Cut-and-Choose技术的安全多方计算协议的主要发展脉络图.

Table 6 Comparison of Protocols in PVC Model表6 PVC安全模型下的协议对比

Fig. 9 Development of MPC protocols based on Cut-and-Choose technology图9 基于Cut-and-Choose技术的安全多方计算协议发展脉络图
5 结束语
本文介绍了密码学协议设计中一个非常重要的Cut-and-Choose技术,并对基于这种方法实现恶意安全、隐蔽安全、公开可验证隐蔽安全协议的发展作了简要介绍.相对于零知识证明、承诺等密码学工具,Cut-and-Choose技术是一种高效的抵抗恶意敌手的解决方法.因此,在早期的研究工作中,被广泛应用于恶意安全模型中,并逐渐发展和完善,产生了许多优秀的工作.
隐蔽安全的概念是为了折中半诚实安全和恶意安全而提出的,具有现实意义.在隐蔽安全模型中,被敌手腐化的参与方可以任意地违背协议的规范,但是却能够被诚实的参与方以一定的概率发现.这种安全性能够提供比半诚实安全更强的安全保障,同时也能达到比恶意安全更好的效率.但这种安全性对敌手的影响是有限的.它只能保证当敌手作弊被发现时,诚实的参与方可以终止协议并放弃与其合作.但是,诚实的参与方不能公开地(可能会泄露其私有输入)说服第三方敌手在协议过程中进行了作弊,这导致敌手依然可以选择在下次计算任务中违背协议.
对此Asharov等人[17]提出了公开可验证的隐蔽安全,具有更强的安全性,可以保证发现敌手作弊的同时,输出一个证书而不会泄露自己的秘密信息,任何第三方依据该证书可以验证敌手的不诚实行为而放弃与它合作.但他们的工作关注的是可行性,依赖于昂贵的signed-OT,与当时最新的半诚实协议相比,没有竞争力.后来Kolesnikov等人[61]作出了各种效率的改进,但是依然需要巨大的开销.
自2019年Hong等人[62]的工作采用更简单的标准OT显著提高了公开可验证协议的效率,引起了更多研究者的关注.然而此时,对于公开可验证的隐蔽安全模型的工作依然针对的是两方场景.此后,相继有3项最新的工作被提出来实现多方场景下的公开可验证隐蔽安全协议.与此前工作不同,这3项工作放弃构造具体协议,采用编译器的方式将安全性较弱的半诚实协议转换为公开可验证的隐蔽安全协议,同时由于离线/在线结构的使用,他们的协议具有较低的开销并且只有常数轮通信.通过编译器,可以自动地将半诚实安全的协议转换成安全性更强的协议.即使未来有新的更加高效的方法或技术来实现半诚实安全协议,但只要该协议满足编译器的转换要求,它也能通过编译器被转换成具有更强安全保证的协议,而不再需要基于这种方法尝试构造出更强安全保障的协议.因此,我们相信,对于以后设计公开可验证的隐蔽安全协议,利用编译器的方式更容易为研究者所接受.
此外,目前基于Cut-and-Choose技术抵抗恶意敌手的工作,已经趋于成熟.通过放松安全模型,这些工作很容易过渡到实现隐蔽安全.而与隐蔽安全相比,这种额外的“公开可验证性”体现在要求电路构造方对混淆电路生成协议副本、OT协议副本以及使用的随机种子进行签名,实现认证性与不可抵赖性.我们认为可以结合区块链等其他具有认证功能的技术与隐蔽安全的研究工作相结合,实现具有公开可验证性质的隐蔽安全协议.相信在不久的将来,会有更多关于公开可验证的安全多方计算工作被提出,并能够用于解决实际问题.

