面向特征继承性增减的在线分类算法

刘兆清 古仕林 侯臣平

(国防科技大学文理学院 长沙 410073)

由于现实环境的开放性与复杂性，在许多实际应用中，人们不得不面临数据的数量与特征维度都在同时变化的情形.一个典型的场景就是数据当前的特征增加，下一时刻的数据特征只有部分被继承，并且由于环境变化难以预知，哪些特征会消失、哪些特征会被继承难以提前确定.本文将这样的数据称为特征继承性增减的流式数据.例如，在环境监测任务中，任意时刻环境中都存在着多种不同寿命的传感器，每个传感器的反馈均被视为一个特征[1]，不同特征因为传感器寿命不同，维持的时间也不同.在寿命较短的传感器失效之前，为维持对环境的观察，会向环境投放新的传感器，使得在某个较短的时期内数据会包含历史特征与新增特征；当这部分寿命较短的传感器失效后，其对应的特征随即消失，而寿命较长的传感器对应的特征将继承到下一时刻.总体来说，这是一个特征先进行增加，然后有继承地减少的过程.

具体地，如图1所示：在T1的初始阶段(绿色部分)，环境中存在2种传感器，返回的数据具有特征S1与S2；在b1阶段，新一批传感器被部署在环境中，数据中新增特征S3，此时数据中共包含3种特征，称为过渡阶段；在T2的初始阶段(蓝色部分)，第1批传感器到达使用寿命之后被销毁，其对应的数据特征S1随即消失，此时数据特征仅剩继承自上个阶段的S2与S3，在b2阶段，又有一批新的传感器被部署在环境中，数据中又会出现新的特征S4.在现实场景中，数据流的特征将随时间不断增加或减少，但由于传感器寿命的差异性，上一时刻数据的特征总有一部分会继承到下一时刻，因此我们将其定义为特征继承性增减的流式数据.

Fig. 1 The feature evolution pattern of environment monitoring图1 环境监测任务中特征的演化规律

传统的在线学习算法要么假设数据以流的形式依次到达但是其特征空间保持不变[2-7]，要么假设特征以流的形式不断到达但是训练数据集保持不变[8-13]，这些都无法直接用于处理特征继承性增减的流式数据.解决该问题一个简单直接的方法是只利用具有相同特征空间的数据进行模型训练，但是这样并不能取得好的预测效果，主要原因有2个：1)部分特征消失后，消失特征对应的权重无法继续利用，在过去的迭代过程中从样本中提取的信息被浪费，产生了信息的损失；2)在新特征出现的初始阶段，具有新特征的样本数量少，不足以充分训练分类器，对分类器的性能造成影响.

解决特征动态变化这一问题的关键就是建立一个能尽可能多地继承原有信息的动态分类模型.基于上述思想，近年来有极少部分工作针对动态特征的场景进行了研究[14-16].这些工作采用不同的特征划分或投影策略来构建动态模型，在处理特征动态变化的问题上做出了原创性的贡献.但是，上述工作假设的数据特征演化方式与本文都不相同，因此相关的技术挑战和解决方法也各不相同.

针对特征继承性增减的流式数据分类问题，本文提出了一种面向特征继承性增减的在线分类算法(online classification algorithm with feature inheritably increasing and decreasing, OFID)及其2种变体OFID -Ⅰ和OFID -Ⅱ.当新特征出现时，OFID引入新权重对其进行学习，对原始特征与新增特征上的分类器制定不同的更新策略，通过结合在线被动-主动(online passive aggressive algorithms, PA)算法[5]与结构风险最小化原则分别更新原始特征与新增特征上的分类器；当部分原始特征消失时，利用历史数据与当前数据的一致性，运用在线矩阵补全的方法，对数据流的缺失部分使用Frequent-Directions算法[17-18]进行恢复，使得原始分类器得以继续更新迭代；为防止出现过拟合现象，开发了OFID算法的2种软间隔变体OFID -Ⅰ和OFID -Ⅱ.理论分析和实验结果分析都验证了本文所提算法的有效性.

本文工作的创新点总结有3个方面：

1) 研究了一个对特征继承性增减的数据流进行分类的新问题，这一问题具有重要的实际应用价值，对该问题进行专门的研究.

2) 设计了一种新颖的算法OFID及其2种变体OFID -Ⅰ和OFID -Ⅱ，从特征继承性增减的数据流中学习高度动态的分类模型.从理论上证明了OFID系列算法的损失上界，保证了算法的可靠性与有效性.

3) 通过对比实验，在公开数据集上与其他算法进行了对比，并取得了良好的表现；同时通过另外2组辅助实验探究了算法的参数敏感程度与时间复杂情况，验证了算法自身的良好性质.

1 相关工作

针对特征动态变化的在线学习研究在实践上具有广泛的应用前景，例如环境监测、垃圾邮件识别等.本文致力于研究面向特征继承性增减的在线学习方法，主要包含2个方面：1)在线学习；2)特征动态变化.下面我们将从这2个方面对本文的相关工作进行概述.

在线学习的研究经历了较长时间的发展，具有成熟的理论与巨大的应用价值[13]，期间发展出许多经典的方法.大致可以将现有在线学习方法分为利用模型一阶信息和二阶信息的方法.利用一阶信息的在线学习算法有感知机算法(perceptron learning algorithm, PLA)[7]、PA算法[5]、在线梯度下降算法(online gradient descent algorithm, OGD)[19]等.感知机算法只在当前模型预测出现错误的情况下才会更新，而PA算法只要当模型产生的预测损失不为0(即使数据标签预测正确)，都会主动更新当前模型.其核心思想是寻找与当前分类模型最近邻的约束，若当前模型对新来数据预测没有损失，模型不更新，否则，模型主动更新，即投影到离现有分类模型最近邻的位置.因此，PA算法在大多数情形下都会显著的优于感知机算法.在线梯度下降算法在每次迭代时都沿当前损失函数梯度下降的方向更新模型，然后将更新后的模型投影到可行域中.利用二阶信息的在线算法有二阶感知机算法[20]、NHERD[21]算法(normal herding method via Gaussian herding)、SCW(soft confidence weighted algorithm)算法[22]、IELLIP(online learning algorithms by improved Ellipsoid)算法[23]、AROW(adaptive regularization of weight vectors)算法[24]等.利用二阶信息的算法有着更优异的预测效果，但是其计算开支与一阶算法相比更大.

以上这些算法建立在数据特征空间固定的基础之上，不能直接在动态特征的场景下进行应用.为解决动态特征场景下的在线学习问题，极少部分研究者结合各种特征演化规律，提出了一些在线动态特征学习算法.Zhang等人首先对数据数量与特征维度随时间不断增加的场景进行了研究，提出了OLSF系列算法(online learning with streaming features)[14].Zhang等人将数量与特征维度都随时间增加的数据称为梯形数据，当新到达的数据携带了新的特征时，OLSF算法将数据特征分为历史特征和新增特征2部分，通过改进PA算法使得分类器在面对2种特征时执行不同的在线更新规则.针对训练集固定、特征以流到来的场景，Wu等人[25]提出了OSFS(online streaming feature selection)算法对数据进行在线特征选择.Hou等人[26]在OLSF的基础上研究了特征有增有减的场景，提出FESL(feature evolvable streaming learning)算法，其假设数据的历史特征是同时消失的，不具有继承性.FESL通过在新增特征与历史特征共存的阶段学习特征之间的映射关系，从而在历史特征消失后可以利用新增特征对历史特征进行恢复，并在2种特征上分别训练分类器，最后利用集成学习的思想对2个预测结果进行集成得到最后的分类结果.在FESL算法的基础上，后续发展了EDM(evolving discrepancy minimization)[27]和PUFE(prediction with unpredictable feature evolution)算法[28]，对FESL场景进行了深入探索和扩展.进一步地，有研究者研究了数据流的特征可以任意新增或消失的情形.如He等人[29]提出了OLVF算法(online learning with varying feature space)，将当前样本的特征分为存留特征、共享特征和新特征3部分，将现有模型投影到共享的特征空间中进行预测更新.Beyazit等人[30]提出了GLSC算法(generative learning with streaming capricious data)，在全特征空间上学习新特征与旧特征之间的映射关系.

2 面向特征继承性增减的在线学习算法

本节首先详细介绍继承性增减的场景以及本文用到的符号和相关含义，然后对OFID算法进行介绍，梳理算法的整体思路，提出相关策略并形成对应的优化问题，然后对优化问题进行求解，在最后给出算法的伪代码.

2.1 问题设定以及相关符号

本文需要完成特征继承性增减场景下的在线二分类任务，本节首先介绍该场景下数据特征的变化特点，后面列出用到的符号与概念，最后抽象为数学形式上的问题.

本场景下数据的变化呈现出明显的阶段性趋势，如图1所示，以数据特征经历一轮完整的继承性增减的时间为一个处理阶段，例如阶段1～T2-b2，不同阶段数据的特征变化非常相似，在处理数据时可以按照阶段进行.每个阶段大致可以分为3个部分，每个部分内数据的特征保持稳定，突变发生在第2，3部分，单阶段内特征变化规律为：

① 1～T1-b1

这段时间内数据的特征空间与第1个样本相同，此阶段的数据具有特征S1与S2；

②T1-b1+1～T1

本阶段的初始，t=T1-b1+1时，特征空间发生突变，数据的维度升高，此时数据携带特征S1，S2与S3，本时段也被称为过渡阶段；

③T1+1～T1+T2-b2

在本阶段，与上个阶段相比，数据特征减少，特征S2，S3得到继承，特征S1消失.

上述场景可以抽象为一个特征继承性增减的在线二分类问题.在本文中用{xt,t=1,2,…,T1+T2-b2}表示序贯接收的样本，其中xt∈dt，表示xt是一个dt维的行向量.wt是t-1轮迭代后得到的分类器.在t=T1-b1+1时，新增特征出现，为了对历史特征和新增特征加以区别，文中用表示原始特征组成的向量，表示新增特征组成的向量，原始特征是样本xt在x1特征空间上的投影，新增特征是样本xt的剩余部分，即其中分类器w做同样的划分，用yt表示样本xt的真实标签，表示分类器的预测结果.

Table 1 Notations and Descriptions表1 符号及其含义

2.2 OFID算法

观察特征的演化规律可以发现算法有2个最主要的问题需要解决，主要问题1：在T1-b1+1～T1阶段，新的特征S3出现，加入训练会对第1阶段训练得到的分类器产生影响；T1-b1+1～T1阶段维持时间较短，数据数少，如何设计更新策略、在初期携带新特征的数据不足的情况下进行较为准确的训练是一个问题.主要问题2：在T1+1～T1+T2-b2阶段，特征S1消失，只利用具有相同特征空间的数据进行模型训练，对应缺失维度的信息就会丢失，造成信息的浪费，降低预测准确率.既要尽可能的减少信息的损失，保证预测准确率，又要适应周期内特征空间的增减变化，这是算法需要解决的技术重点，针对特征继承性增减的在线分类场景，本文提出面向特征继承性增减的在线分类算法OFID及其2种变体.对于问题1，算法的策略是在第2阶段更新时引入新分类器对新增特征进行学习，但尽量维持上个阶段分类器的权重.历史模型在原始特征的多轮迭代上得到了充分训练，具有较高的置信度，因此采用维持原有分类器的更新策略，进行上述处理，模型可能会增加对旧特征的依赖，对于该问题，OFID算法在下个处理过程中，放弃了对于旧特征的恢复，只对新分类器进行训练，在一定程度上避免了模型对旧特征的依赖，达到了充分拟合新特征的目的；对于问题2，本文采用FD算法对矩阵进行补全.补全后的数据矩阵可以采用已有的成熟技术进行在线分类.

本文在第1部分采取PA算法进行模型更新，因为PA算法具有十分显著的优点：1)PA算法是在线学习任务中应用十分广泛的算法，具有良好的收敛速度；2)PA算法在保证良好学习性能的前提下，具有较快的运行速率；3)利用PA算法可以使OFID算法具有良好的理论保证.因此本文使用PA算法进行模型更新.

本场景下数据呈现明显的特征增减规律，在1～T1-b1时间段内，特征空间保持不变，本阶段内第t轮迭代时，PA算法满足的优化表达式为

(1)

(2)

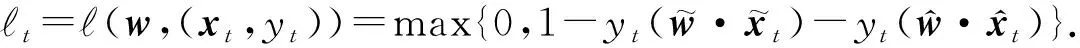
以上处理解决了特征增加时分类器对新增特征的适应问题。然而，在T1+1～T1+T2-b2阶段，特征S1消失，数据矩阵出现了缺失.为了继续使用和训练原有分类器，算法选择利用过渡阶段的完整数据进行矩阵补全.

在传统特征变化的研究中[26,31]，通常采用新特征来补全旧特征，达到挖掘新旧特征之间的关系的目的.然而，本文研究的特征继承性增减的实际应用场景中，下一时刻数据哪些特征会发生缺失无法事先确定，难以通过学习新旧特征之间的关系来对消失的旧特征进行补全.因此，本论文采取FD算法进行补全，FD算法的基本思路是寻找出现频率高的向量作为一组基来补全数据矩阵，将单个的数据样本作为整体来处理，可以很好地解决新旧特征不确定的问题，对缺失特征进行有效准确的补全.

FD算法不考察特征之间的关系，其补全流程是建立一个r行的矩阵，最后一行设置为零向量，每一个样本被接收后作为一个行向量替代掉矩阵中的零向量，然后对矩阵做SVD分解，将最小的奇异值剔除，继续按照以上步骤操作，遍历所有数据.最终返回一个草图矩阵.

T1-b1+1～T1阶段接收到的样本组成矩阵N，对矩阵N使用FD算法绘制秩为r的矩阵草图B，记B的行向量为vi,i∈{1,2,…,r}，构成一个向量组，B的行空间记为V，利用V对T1+1～T1+T2-b2阶段的缺失部分进行补全.

在T1+1～T1+T2-b2阶段的第t轮迭代，接收到样本xt，在V中寻找一个向量zt，记zt∈V，该向量满足:

(3)

(4)

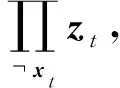
(5)

(6)

第2个是ξ的平方形式：

(7)

(8)

以此形成2种变体算法OFID -Ⅰ与OFID -Ⅱ，它们是OFID算法的软间隔形式.

传统的在线学习算法每次接收一个数据就进行模型的更新，因此具有运行速度快、存储空间要求小等优点，而本文提出的OFID系列算法每次接收一个数据就进行分类器的更新，具有传统在线学习算法的优点，属于典型的在线学习算法.但由于本文的核心研究内容是特征继承性增减这一特殊场景，作者在传统的在线学习算法上做出了改进，提高了算法对特征继承性增减变化的适应能力，增强了算法在该场景下的分类能力.

2.3 优化问题求解

(9)

其中τ是拉格朗日乘数，将w的表达式代入L(w,τ)，进一步有:

(10)

式(10)对τ求导，令其等于0，得到wt+1的闭式解：

(11)

优化问题式(2)的求解与问题式(1)的求解类似，使用拉格朗日乘子法，有:

(12)

(13)

式(13)对τ求导，令其等于0，得到wt+1的闭式解：

(14)

继续使用拉格朗日乘子法对优化问题式(5)～(8)进行求解，得到2个变体算法统一的更新方式，

(15)

其中，

(16)

综合以上求解过程，3种算法具有统一的更新形式：

OFID算法及其他2种变体算法的伪代码如下所示：

算法1.OFID算法及其变体.

输入：参数C>0;

输出：1～T1+T2-b2阶段内预测正确的样本数量、草图矩阵B.

初始化：w1=(0,…,0)∈d1;

fort=1,2,…,T1do

① 接收样本xt;

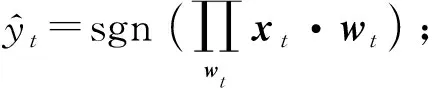
yt(w·xt)}，wt与xt维度相同时；

wt与xt维度不同时.

④ 接收标签yt;

⑤ 计算步长τt;

⑥ 利用算法2训练草图矩阵B;

⑦ 更新分类器：

end

fort=T1+1,…,T1+T2-b2-1 do

⑨ 重复步骤②③④⑤⑦

end

算法1中采用了Frequent-Directions学习草图矩阵，其算法伪代码为：

算法2.Frequent-Directions.

输出：草图矩阵B;

初始化：B=0r×dT1.

fort=T1-b1+1,…,T1do

①Br←xt;

② [U,Σ,V]←SVD(B);

③N←ΣVT;

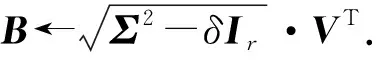
end

3 算法分析

本节对OFID系列算法的损失进行讨论与证明，在理论上保证算法的有效性和可靠性.本节用到了3个引理、3个定理.引理1用于说明FD算法在条件满足的情况下可以精确地对矩阵进行补全；引理2，3与定理1用于说明数据集线性可分情况下OFID算法Hinge损失平方和有上界；定理2用于说明算法OFID -Ⅰ犯错总数有上界；定理3用于说明算法OFID -Ⅱ的Hinge损失平方和有上界.

引理1.在算法2中，对矩阵B做SVD分解，B=UΣVT，令r∈{min(T1-b,d1)}，即r是草图矩阵B的秩，并且有U=(u1,u2,…,ur)∈(T1-b)×r，V=(v1,v2,…,vr)∈(T1-b)×r，记和是矩阵B的前r个左右奇异向量.定义:

若满足s≥7μ(r)rln(rb1/δ)，s为消失特征的维数，则在至少1-δ的概率下算法可以将矩阵精确地进行恢复.

证明.引理1的详细证明可参考文献[18].

引理2[14].记(xt,yt)，t=1,2,…,T为序贯接收的流式数据，其中xt∈dt，yt∈{-1,+1}，数据的维数满足dt-1≤dt，步长损失t采用Hinge损失，则对任意向量u∈dT，有:

(17)

即:

下面对单项的∇t进行估计.在t=0时，τt=0，有又dwt≤dwt+1，则有:

(18)

(19)

式(19)两边对t累加，可得:

(20)

证毕.

引理3[14].记(xt,yt)，t=1,2,…,T为序贯接收的流式数据，其中xt∈dt，yt∈{-1,+1}，dt-1≤dt并且对所有t均成立；假设存在分类器u∈dT，在任意一次迭代中满足则有：

(21)

(22)

证毕.

定理1.记(xt,yt)，t=1,2,…,T1+T2-b2为序贯接收的流式数据，其中xt∈dt，yt∈{-1,+1}，补全后的样本满足对所有t均成立；分类器满足对所有t均成立；假设存在分类器u∈dT，对补全后的矩阵，对任意的t满足令R=max{R1,R2}，则有:

证明.令：

∇t对t进行累加，得到:

证毕.

定理2.记(xt,yt),t=1,2,…,T1+T2-b2为序贯接收的流式数据，其中xt∈dt，yt∈{-1,+1}，补全后的样本满足对所有t均成立，则对于任意向量u∈dT1，算法OFID -Ⅰ犯错次数的一个上界为

证明.令

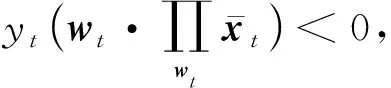
代入后得到式(21)中，得到:

整理后得到:

证毕.

定理2说明了算法OFID -Ⅰ在恢复出的样本有界时，犯错总数存在上界.

定理3.记(xt,yt),t=1,2,…,T1+T2-b2为序贯接收的流式数据，其中xt∈dt，yt∈{-1,+1}，补全后的样本满足对所有t均成立，则对于任意向量u，u∈dT1，有:

证明.通过引理2已知:

(23)

(24)

将τt的定义代入，有:

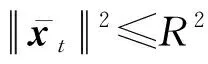
通过定理3，在理论上验证了OFID -Ⅱ算法的Hinge损失平方和有上界.

证毕.

4 实 验

本节通过数值仿真实验来验证OFID算法及其2种变体的表现.首先介绍实验设置及数据集.

本节共设置4组实验，组1实验为主试验，进行OFID系列算法与FESL-c，FESL-s，PUFE算法的对比，使用预测准确率作为指标，观察OFID系列算法在具体数据集上的表现，验证OFID算法的有效性和可靠性；组2实验为参数实验，以预测错误率为指标，考察2种变体算法的参数敏感性以及添加松弛变量的效果；组3实验为算法时间复杂的实验，指标为时间，用来考察算法的时间复杂度.组4实验为辅助实验，指标为算法的预测正确率，在3个不同的迭代阶段分别记录并进行对比，验证OFID算法在不同迭代阶段的有效性.

实验数据要求具有动态的特征空间，为满足这一要求，对特征空间进行了划分，划分的样式如图1所示，每个数据集的特征随机进行排序，近似均分为3部分；在场景设置中T1-b1+1～T1阶段维持时间较短，在划分数据集时遵循了这一设定，过渡阶段的数据量占比设置为1/10，阶段1的数据比例与缺失数据的比例等同，我们按照以上规则对数据集进行划分.

每次实验每个数据集重复20次，每次重复随机打乱数据的顺序，并使用20次结果的平均值作为指标的最终值.参数实验中，总共进行9次调参，参数C的选择范围为10-4～104，参数C的每次变化倍率为10.

本文在公开数据集上进行实验，包括Cancer，air，WDBC，warpPIE，WBC，Haberman，Wine，Thyroid，Seeds共9个数据集，这些数据集分布在多个领域.数据集的情况如表2所示：

Table 2 The Datasets Used in the Experiments表2 实验中用到的数据集

4.1 OFID系列算法与FESL,PUFE算法的对比实验

表3展示了6种算法在不同数据集上的最终预测准确率.在大多数数据集上，OFID系列算法与其他算法相比有着较高的预测准确率，说明OFID系列算法较好地适应了数据特征的动态变化，具有现实应用的价值.但是一个学习过程中，3个阶段的数据的特征有较大的差异，因此最终的预测准确率并不足以概括在整个学习过程各个算法的表现.为更加直观地观察算法在各个阶段的表现，本文选取预测错误率作为指标，观察6种算法在学习过程中预测错误率的动态变化，实验结果如图2所示.

Table 3 Prediction Accuracy of Six Algorithms on Different Datasets表3 6种算法在不同数据集上的预测准确率

Fig. 2 Prediction wrong rates of six algorithms on different datasets图2 6种算法在不同数据集上的预测错误率

图2是6种算法在数据集上预测错误率随时间的变化情况，横坐标是迭代次数，纵坐标是平均预测错误率.OFID -Ⅰ，OFID -Ⅱ在大多数数据集上表现优于算法OFID.说明软间隔形式取得了应有的设计效果，降低了对噪声的敏感程度，提高了算法性能.

在大多数数据集上，OFID -Ⅰ(红色)、OFID -Ⅱ(黑色)算法表现最好，算法OFID(蓝色)次之，表现优于其他3种算法，说明OFID系列算法具有实际应用的价值，该实验验证了算法的有效性.

算法FESL，PUFE在数据集Wine上表现较OFID更好.在其余数据集上，OFID系列算法表现最优.对于上述实验结果进行观察，会发现1～T1-b1阶段的预测正确率对算法FESL，PUFE的整体表现有重要的影响，FESL，PUFE的整体表现优于OFID系列算法时在1～T1-b1阶段的预测优于OFID系列算法.

4.2 参数实验

在本节进行参数实验，评价指标为20次实验的平均预测正确率，观察参数变化对实验结果的影响，考察OFID系列算法对参数C的敏感程度，图3为参数实验的具体结果，横坐标为参数C的数值，参数C的范围为10-4～104，纵坐标为平均预测正确率.OFID算法无参数，不受参数变化影响，形成实验的固定参照；观察图3，随着参数C的变动，可以发现OFID -Ⅰ，OFID -Ⅱ的预测正确率随之产生了一定程度的波动.参数过小时，OFID算法与OFID -Ⅰ，OFID -Ⅱ算法之间的预测正确率存在差距，但随着参数C逐渐增大，3种算法准确率之间的差距先增大后减小，最后趋同.

从优化问题的结构来分析出现图中变化趋势的原因，参数C调节的是优化表达式中松弛变量与分类器变化2部分的比率，当C增大时，要最小化优化问题式(5)～(8)，代表着松弛条件收紧，对应的ξ值变小，损失降低，对数据的敏感性提高，随着参数C增大，2种变体算法逐渐向没有松弛变量的OFID算法靠拢，分析结果刚好与图3的实验结果对应.

Fig. 3 The average rates of right predictions with respect to C=10i图3 C=10i对平均预测正确率的影响

4.3 算法的时间复杂的实验

本节实验中，评价算法计算复杂度的指标为算法得到预测结果的运行时间.6种算法在不同数据集上的运行时间如表4所示.

Table 4 Running Time of Different Algorithms on Different Datasets表4 不同算法在不同数据集的运行时间 s

6种算法的更新表达式在形式上并无本质上的不同，均为线性迭代算法，区别只在于每一步迭代中使用的系数，这并不会有时间消耗上的显著差异，因此，复杂度存在差异的主要原因在于矩阵补全的方式.OFID系列算法与PUFE算法均使用FD算法进行补全，FESL算法在过渡阶段训练一个线性映射进行补全，这涉及到了矩阵的求逆运算.这也是时间消耗的主要部分.

表4中OFID -Ⅰ与OFID -Ⅱ算法的运行时间明显高于其他算法，这是因为这2种算法需要进行参数的调节，每得到一个调参后的预测结果，算法需要运算9次，平均得到一个结果的时间与其他算法相当；OFID算法与FESL算法、PUFE算法在时间消耗上相当，具有相同的计算复杂度.

4.4 分阶段预测实验

本节实验中选取4个数据集，观测指标为OFID系列算法与其他3种对比算法在3个不同阶段的平均预测准确率，预测结果取阶段结束时算法的平均预测准确率，具体的实验结果如图4所示.观察实验结果，可以发现OFID系列算法在迭代的3个阶段里均有优异的表现，这组辅助实验充分说明了OFID系列算法在不同迭代阶段均具有良好的分类性能.

Fig. 4 The average prediction accuracy of the algorithm in three periods图4 3个迭代阶段中算法的平均预测准确率

5 总结与展望

为解决数据流特征继承性增减这一新的实际问题，本文提出了一种面向特征继承性增减的在线学习算法OFID及其2种变体OFID -Ⅰ与OFID -Ⅱ.当新特征出现时，通过结合在线PA算法与结构风险最小化原则分别更新原始特征与新增特征上的分类器；当原始特征消失时，对数据流使用Frequent-Directions算法对数据矩阵进行补全，使得原始分类器得以继续更新迭代.理论分析和实验结果分析都验证了本文所提算法的有效性.

本文的对比方法中，有一些优秀的思想可以进行借鉴，例如对新旧分类器分别进行预测更新，互不干扰，预测标签来自新旧分类器的预测结果进行加权，这样不仅避免了分类器对旧特征的过渡依赖，并且可以充分利用恢复出的信息，有着较高的研究价值，这将是未来工作中我们努力的一个方向.

本文所提的算法主要是针对线性场景下的分类问题，因此，将本文算法扩展到非线性场景下是我们未来非常重要的一项工作.同时，如何挖掘特征继承性增减数据流的更多信息，例如二阶信息、数据分布信息，以及如何对特征继承性增减数据流进行在线聚类等也是值得关注的方向.因此，在未来的工作中我们将对上述内容开展更加深入的研究.