变限积分函数求导公式的应用探讨
黄 翔,李小新
(1.安徽中医药大学医药信息工程学院,安徽 合肥 230012;2.池州学院大数据与人工智能学院 安徽 池州 247000)
变限积分函数是一种特殊的函数表示方法,它用定积分的形式解决了在闭区间上连续函数的原函数存在性问题.教学中,变限积分函数的求导问题是教学的重点与难点,也是考试常考知识点,因此对变限积分函数的求导方法探讨是教学研究的热点之一.
文传军等[1]将积分变限的函数求导问题归纳为公式型、乘积型和换元型,并给出了通用的基于复合函数形式的含积分变限函数求导方法.宋传静[2]由易到难依次给出五个求导公式,并结合例题比较五个公式的解题过程的难易度.朱忠华[3]结合实例讲解变限积分函数的求导以及其在微积分各主要内容中的应用.熊良鹏等[4]探讨了变限积分函数的求导性质在极限计算及积分不等式证明两类问题的应用.侯玉双等[5]针对学生在学习变限积分函数求导数时通常出现的三类错误,结合牛顿-莱布尼兹公式,提出了变限积分函数求导的F-方法.品希大[6]探讨了一元函数变限积分函数及其导数的教学方式,举例并归类说明不同类型题目如何正确用积分函数求解.陆宜清[7]介绍由变限积分函数所衍生的积分函数,讨论了变限积分函数在证明定积分性质方面的应用.
本文例举变限积分函数求导公式在近十年的全国大学生数学竞赛和硕士研究生入学考试试题中若干应用,以期对同学们后续课程学习、数学竞赛、考研、进行学术研究等方面提供必要帮助.
1 定义与公式
如果函数f(t)在区间[a,b]上可积,x∈[a,b],则变动上限的积分是关于x的函数,称为变上限积分函数.同理称为变下限积分函数,统称为变限积分函数.
变限积分函数求导问题是高等数学课程考查的重点,在张磊等[8]中可以查阅以下求导公式,在此不给证明.
需要指出的是,公式(1)是沟通导数与定积分的桥梁,是后面公式的基础,公式(2)是公式(1)的推广,是变限积分函数求导的一般公式,在平时教学中应用较多,特别注意,该公式是被积表达式中不含有求导变量x时才能使用;公式(3)是被积函数含参变量的积分函数的求导公式,显示积分函数求导过程中,求导与求积次序可以互换,公式(4)是含参变量的变限积分函数的求导公式,作为其推广,公式(5)是对被积函数是复合函数含参变量的变限积分函数求导.
特别地,对于含参变量的变限积分函数的求导一般可通过“变量分离和变量替换”将含参变量的变限积分函数转换成直接可以用公式(1)、(2)求解的形式.
2 应用举例



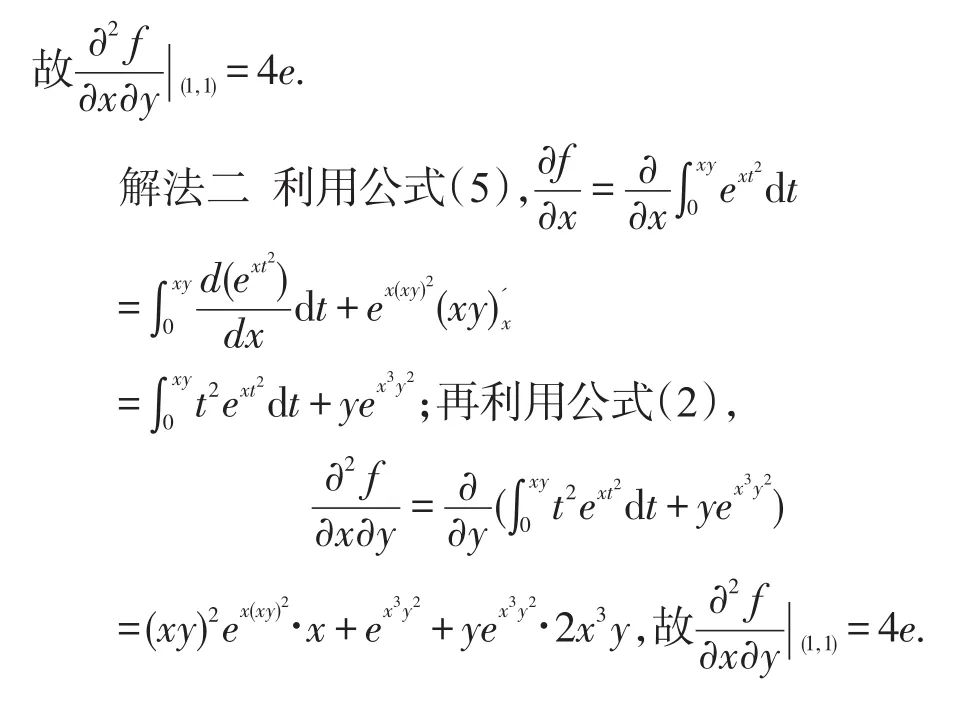
3 结论
变限积分函数是一类非常重要的特殊函数,它的求导公式必须熟练掌握并能进行各方面的应用。应用时要注意区分积分变量、函数参变量以及函数的复合形式,采用变量分离和变量替换时与常义积分相似,需要遵循“换元必换限”的原则.公式(5)更具有一般性、直接性、适用范围广的优势,但是也具有形式复杂,记忆理解困难的特点.在教学中,建议根据学生基础,讲解深度需难易结合,既能吸引学生学习兴趣,又能避免学生产生畏难、排斥心理.

